NCERT Maths Chapter 10 Circles Class 10 Solutions - Free PDF Download
NCERT Solutions for Class 10 Maths Chapter 10 Circles



FAQs on NCERT Solutions for Class 10 Maths Chapter 10 Circles
1. Why Should I Choose Vedantu?
Vedantu is the number one online education platform where students find the best study material all over India. They have provided NCERT solutions based on CBSE guidelines, lots of Mock Test Papers, unsolved and solved questions, previous year questions papers, and many other things to make study easy.
Students can download them from the online platform of Vedantu and can practice regularly. Also, we provide online lectures, videos, and seminars with experts where students can ask their problems regarding education. Our experts guide them and give the best solutions.
2. Tell Me in Detail about the Concepts of Class 10 Chapter 10 Maths (Circles)?
Circle chapter is wholly based on subtopics of circles like tangents, theorems, and others. Here, we have mentioned all topics in bullet form. Have a look below before going to learn them:-
Introduction to a circle- basic concepts including new terms and meaning of the circle
Tangent to a circle- theorems based on a tangent concept, proof, and problems related to the same
Number of a tangent from a point to a circle- problems and proof along with construction techniques
So, these are the main topics of the Circle chapter. Students should learn them in brief to avoid any hassle in a numerical problem.
3. Do You Know How Many Tangents a Circle Can Have Normally?
Usually, there is no limit of tangents a circle can have. It can be infinite because a circle is made up of infinite points that are in an equal distance from a point. Since there are infinite points on a circle's circumference, infinite tangents can be drawn from them.
We have given this question because, in board exams, these types of questions have also asked. Students should clear their basic concepts and learn definitions and theorems to score good marks in this chapter.
4. How many sums are there in Chapter 10 “Areas Related to Circles” of Class 10 Maths ?
There are a total of three exercises in Chapter 10 of CBSE Class 10 Maths. All of these exercises consist of several questions that are related to circles. You need to practise each one of these questions very thoroughly. All the questions are designed to cover the whole syllabus and all the important topics. At Vedantu, you will find all the solutions to this chapter.
5. What will students study in Chapter 10 “Areas Related to Circles” of Class 10 Maths?
In Class 10 Maths, for every chapter, it is very important to understand and learn the basic concepts of Maths. Even in Chapter 10, which deals with Circles, you have to study the concepts of a circle. Then, you will study the different components of a circle and how to measure the area and perimeter of a circle. After that, you will learn how to solve various problems related to the concepts of this chapter.
6. Why are NCERT Solutions of Chapter 10 of Class 10 Maths important?
NCERT Solutions of Class 10 Maths Chapter 10 provides you with the proper system and steps to solve various kinds of problems related to the chapter. If you follow your solutions, you will know how to properly solve each type of numerical. Also, you can use the solutions as a reference to check your answer to the exercise questions.
7. What are the important topics covered in NCERT Solutions for Class 10 Maths Chapter 10?
The important topics covered in NCERT Solutions for Class 10 Maths Chapter 10 are basic concepts of a circle, the components of a circle, how to calculate the area of a circle, how to calculate the perimeter of a circle, how to solve various kinds of questions related to the circle and its components. These are the basic important topics that are covered in NCERT Solutions for Class 10 Maths Chapter 10.
8. Where can I get solutions for Chapter 10 of NCERT Class 10 Maths?
You can get solutions for NCERT Class 10 Maths Chapter online on Vedantu app and website. Vedantu is the best website for getting solutions for all NCERT subjects for all the classes free of cost. It contains chapter-wise solutions for every chapter of every subject. The answers that are provided on Vedantu are very accurate and are well detailed. The solutions help students understand the topics very well and prepare better for their examinations.
9. How to solve circle questions in class 10?
There isn't a one-size-fits-all approach for solving circle problems, but here are some general tips:
Identify the Key Concepts Involved: Recognize terms like radius, diameter, chord, secant, tangent, arc, sector, etc. Understand their definitions and relationships.
Visualize the Circle: Sketch a diagram to represent the problem. Mark the given information and what you need to find.
Apply Relevant Formulas: Circle properties have specific formulas like circumference (2πr) and area (πr²). Use them appropriately.
Geometric Relationships: Circles often involve geometric properties like Pythagoras theorem or angle relationships. Use these connections when applicable.
Logical Reasoning: Break down complex problems into smaller, solvable steps. Consider using indirect methods if necessary (assuming the opposite and proving it leads to a contradiction).
10. What is the formula for all areas of circle Class 10?
There's only one formula for the area of a circle in Class 10, and it is:
Area of circle = πr²
Here, π (pi) is a mathematical constant with an approximate value of 22/7 or 3.14 (you can use the value provided in your textbook or exam instructions). "r" represents the circle's radius (distance from the center to any point on the circle's edge).
11. How many theorems are there in circle Class 10?
The specific number of theorems covered in circles for Class 10 may vary depending on your curriculum, but some common ones include:
Angles in the same segment are congruent.
Angles formed at the center by the same chord are congruent.
The angle subtended by an arc at the center is double the angle subtended by the same arc at any other point on the circle's circumference.
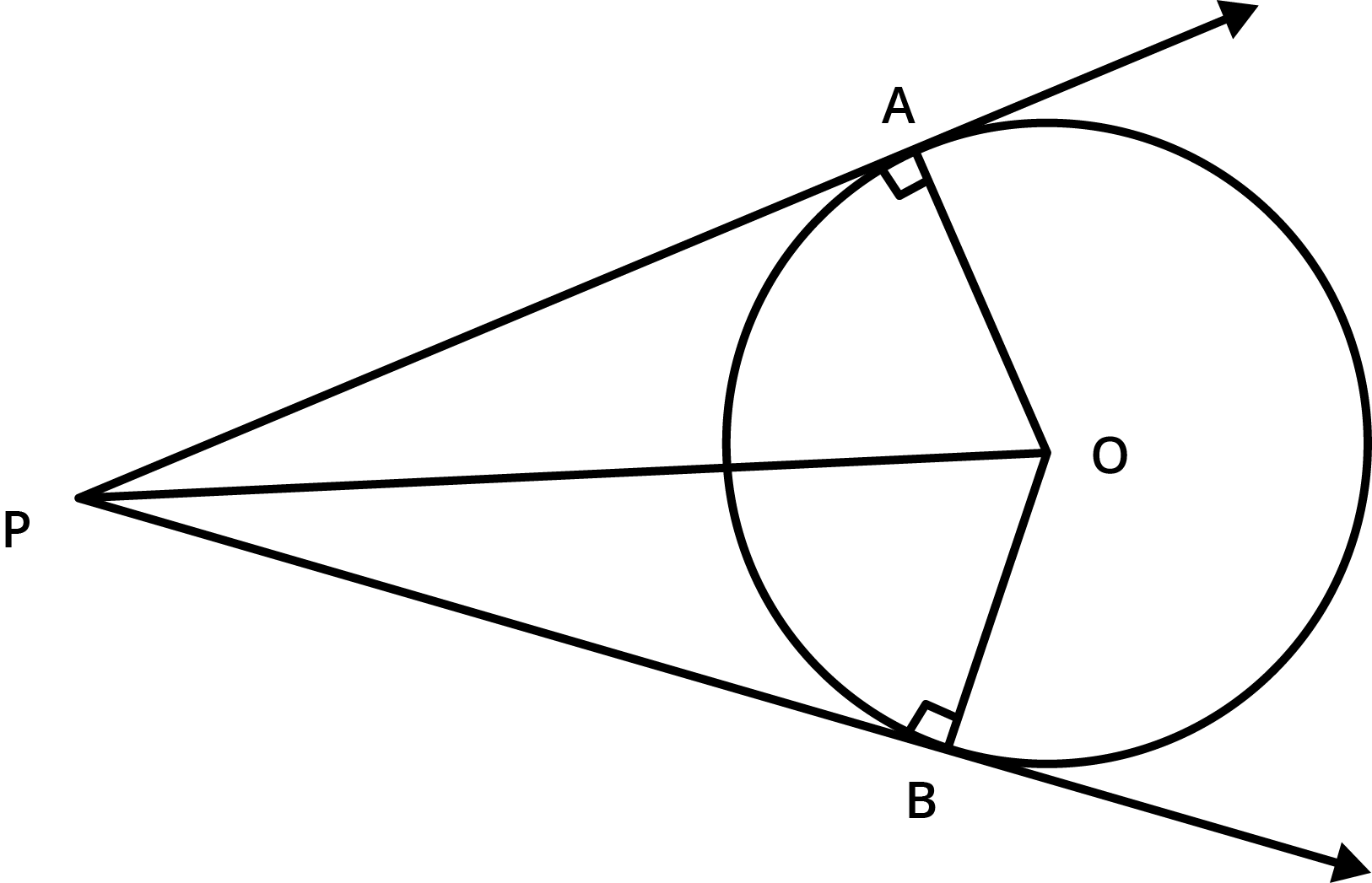
The tangent drawn at a point on a circle is perpendicular to the radius passing through that point.
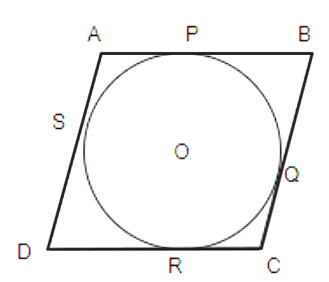
Lengths of tangents drawn from an external point to a circle are equal.
There may be additional theorems or properties covered in your specific course.
11. How many exercises are there in circle class 10?
The number of exercises on circles in Class 10 depends on your textbook or resource material. It's generally not specified in the overall circle concept but rather spread across different sections related to circles (tangents, secants, etc.).
12. What is the first theorem of the circle Class 10?
The order of theorems might differ slightly based on your curriculum, but a common first theorem related to circles is:
Angles in the same segment are congruent.
This theorem states that if you draw two chords within a circle that creates a segment (an enclosed area), the angles formed by those chords at the circle's circumference will be equal.
13. What is a secant of a circle Class 10?
There might be a typo in your question. In circles, we deal with secants (not "sectant"). A secant is a line that intersects a circle at two distinct points. Imagine a straight line that cuts through a circle in two places. That line is a secant.




















 Watch Video
Watch Video




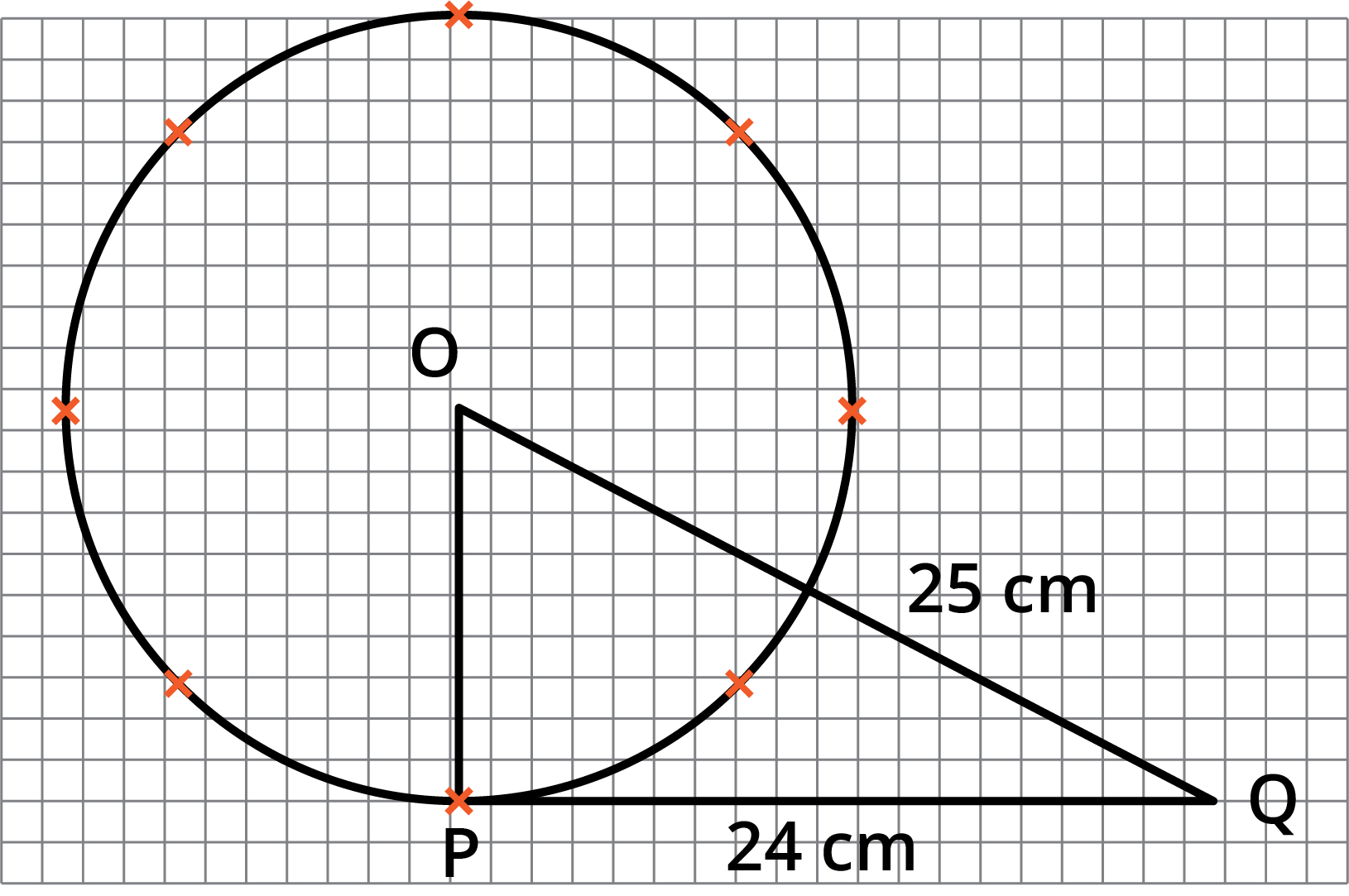
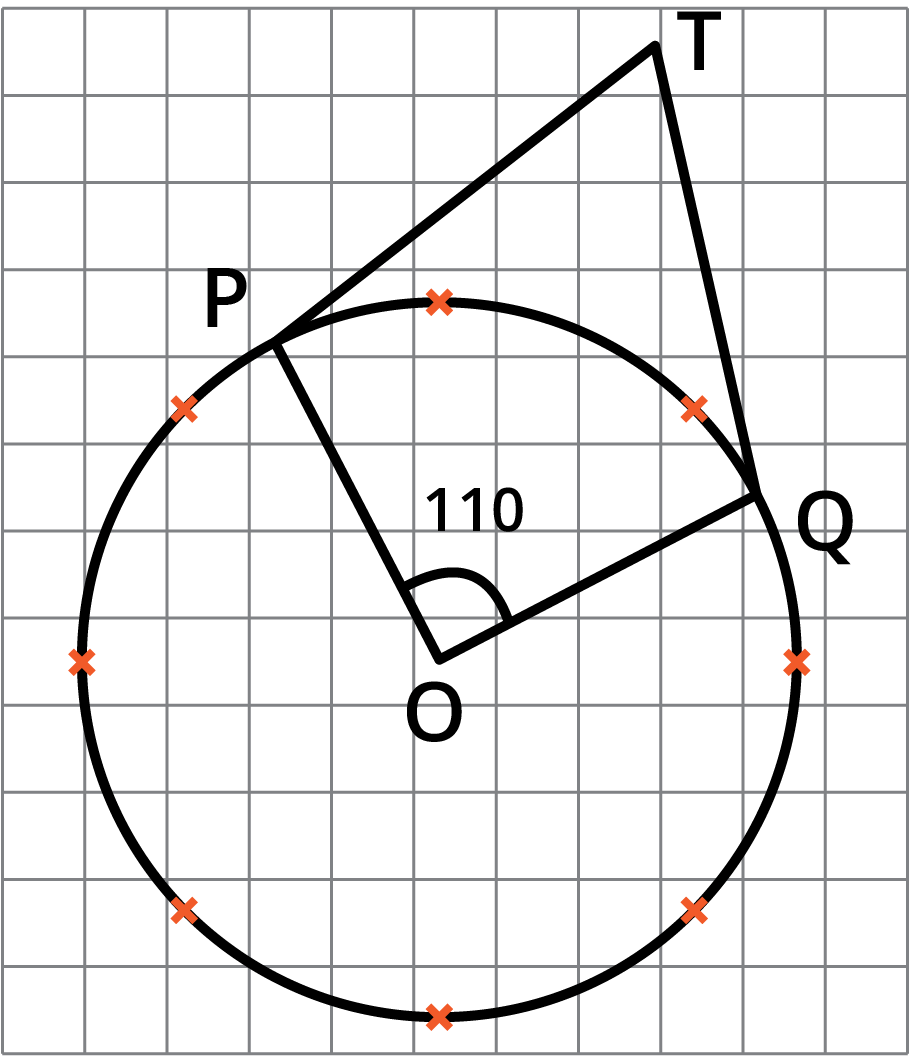


![The length of a tangent from a point \[A\] at distance \[5\ \text{cm}\] from the centre of the circle is \[4\ \text{cm}\].](https://www.vedantu.com/seo/content-images/eb745167-72ab-43c5-afd0-b50d06bbb585.png)
![Two concentric circles are of radii \[5\ \text{cm}\] and \[3\ \text{cm}\]](https://www.vedantu.com/seo/content-images/4ae23b52-8e21-42f2-9dbd-61c1e56c4022.png)
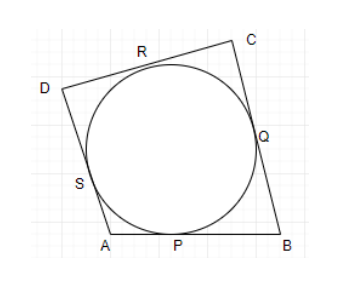
![\[XY\] and \[X'Y'\] are two parallel tangents to a circle with centre \[O\] and another tangent \[AB\] with point of contact \[C\] intersecting \[XY\] at \[A\] and \[X'Y'\] at \[B\]](https://www.vedantu.com/seo/content-images/d7c1ab06-ceb6-4ab7-bc2c-70e44f7d3ca9.png)
![A triangle \[ABC\] is drawn to circumscribe a circle of radius \[4\ \text{cm}\] such that the Segments \[BD\] and \[DC\] into which \[BC\] is divided by the point of contact \[D\] are of lengths \[8\ \text{cm}\] and \[6\ \text{cm}\] respectively](https://www.vedantu.com/seo/content-images/5ad089ce-f737-4b35-a21d-6c10294c57f1.png)