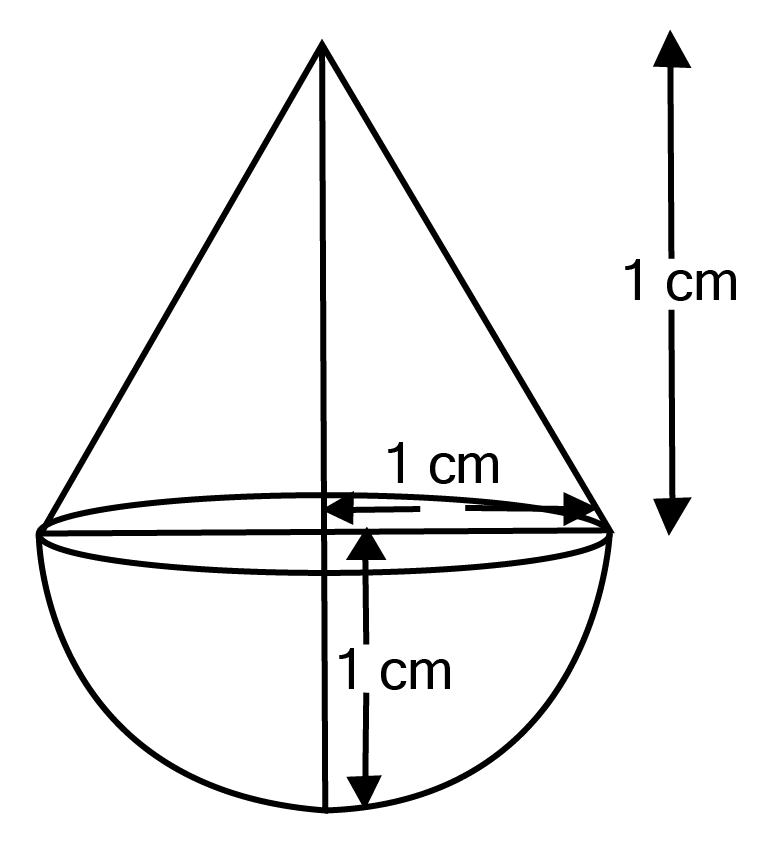
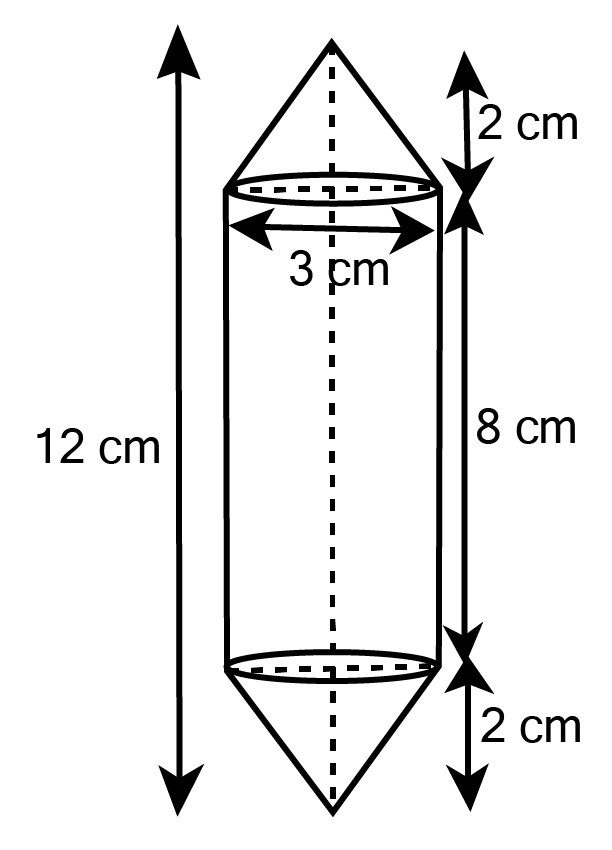
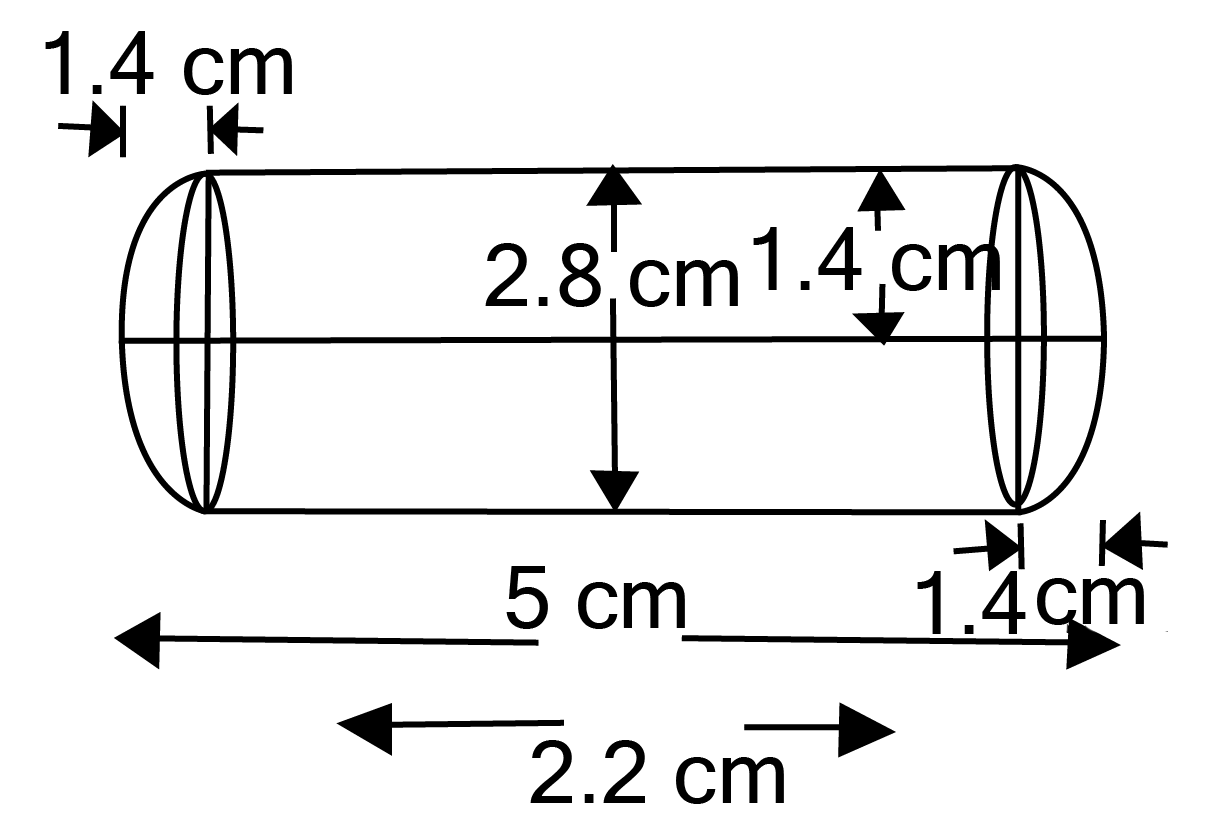
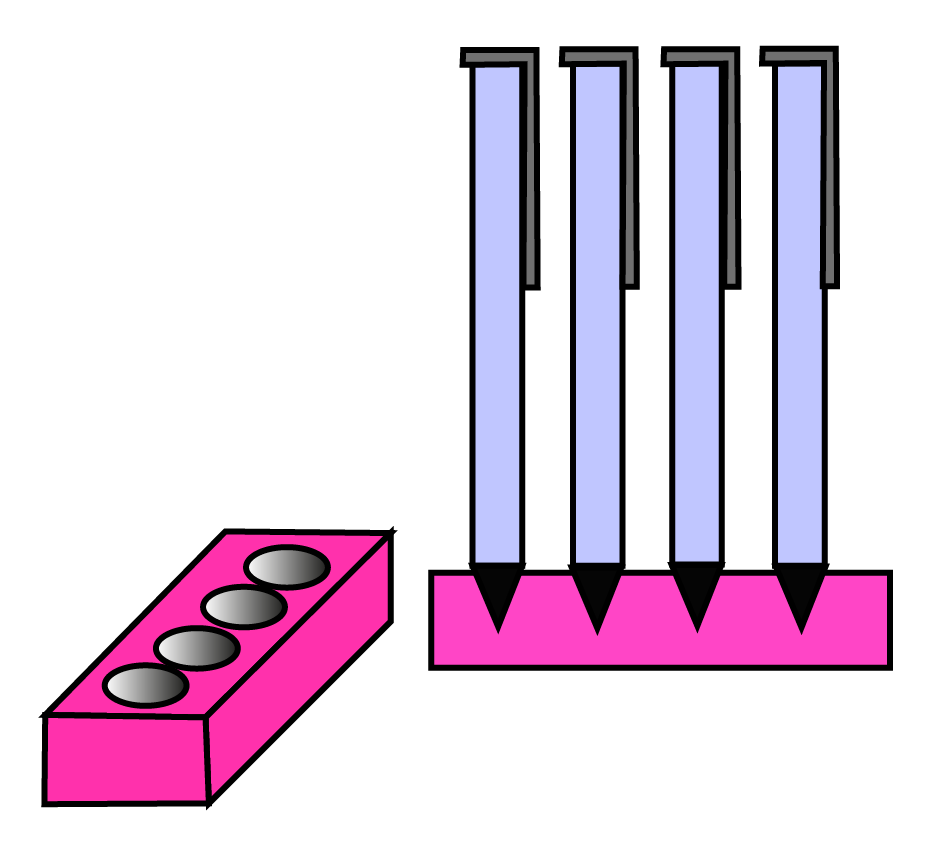
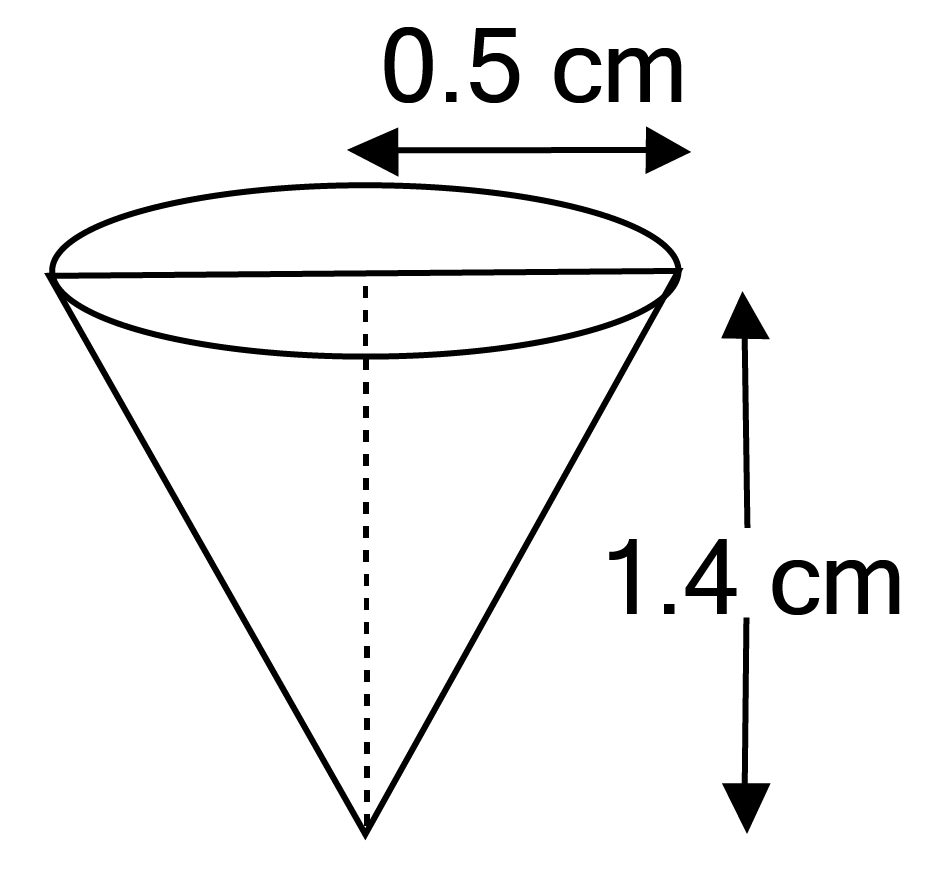
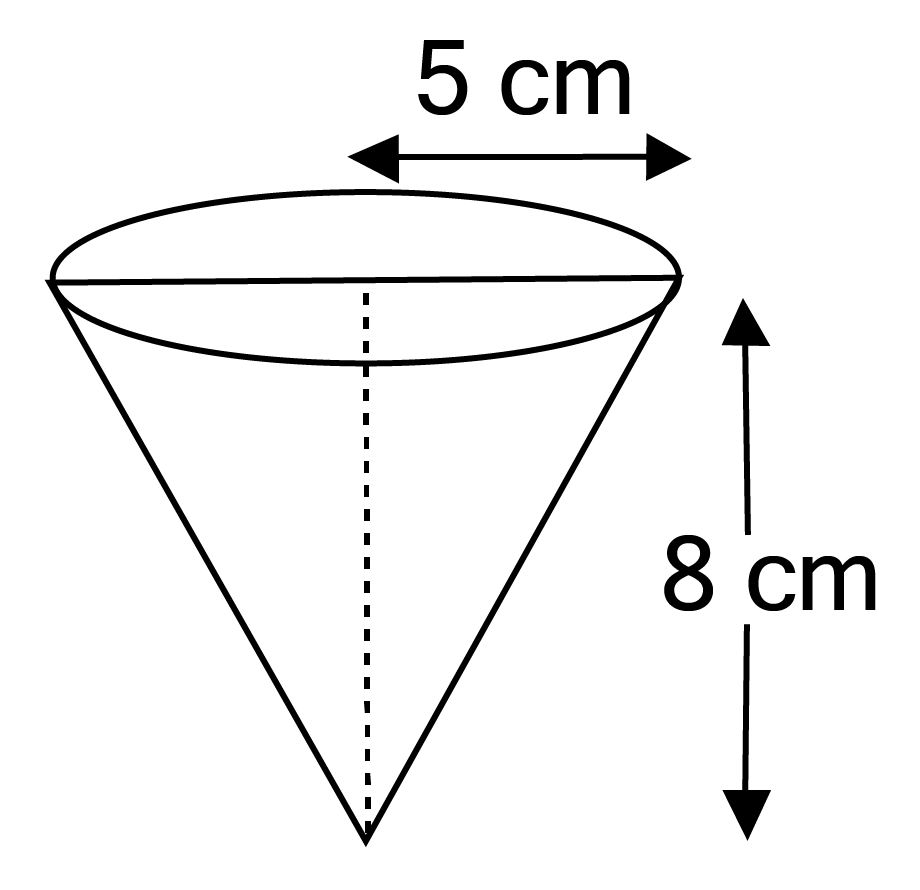
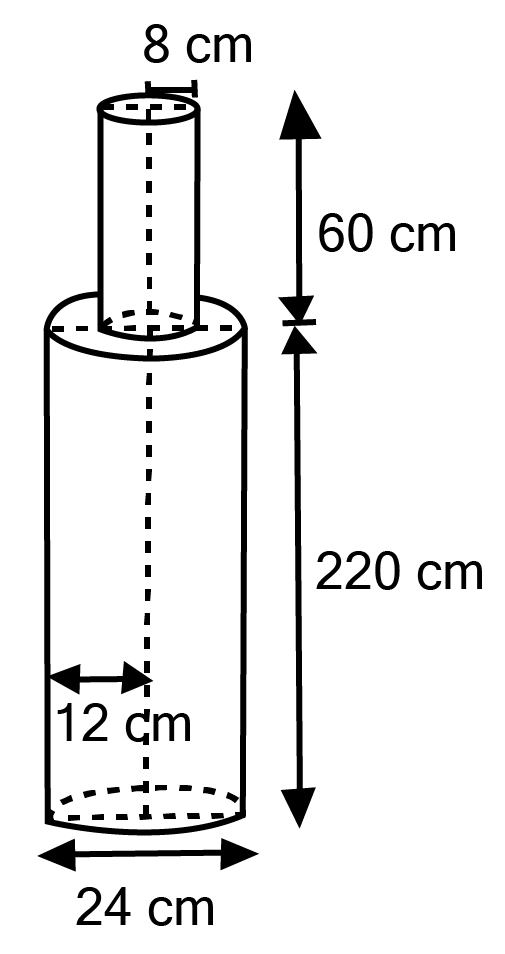
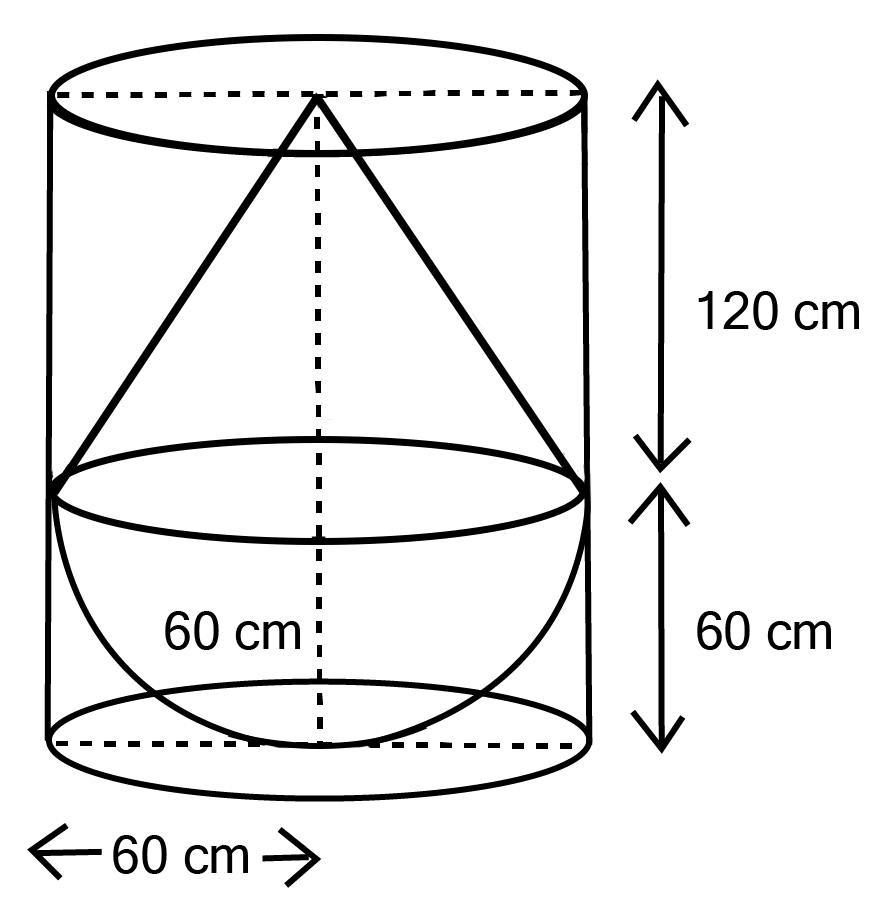
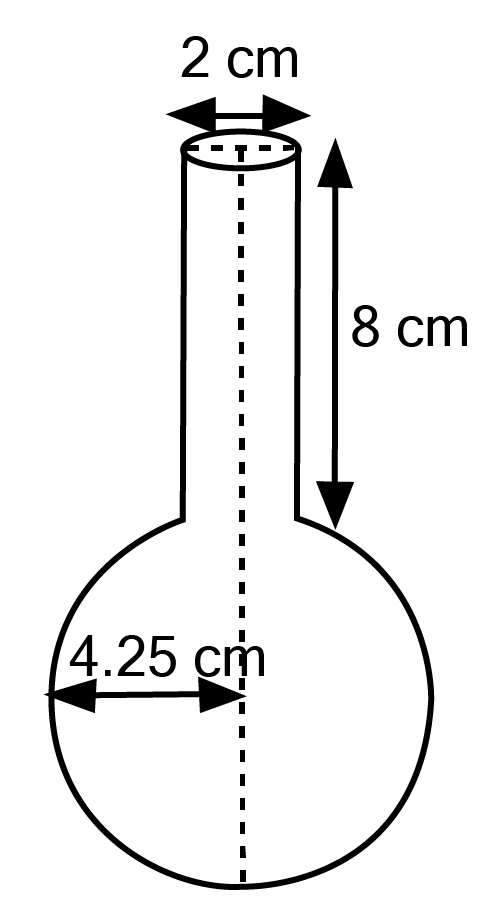
Class 10 Maths Chapter 12 Exercise 12.2 Solutions for Surface Areas and Volumes: FREE PDF
Class 10 Maths Chapter 12 Exercise 12.2 Surface Areas and Volumes NCERT Solutions
FAQs on Class 10 Maths Chapter 12 Exercise 12.2 Surface Areas and Volumes NCERT Solutions
1. What are the key topics covered in the NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas and Volumes?
The NCERT Solutions for Class 10 Maths Chapter 12 focus on:
- Surface areas and volumes of basic 3D shapes (cube, cuboid, cylinder, cone, sphere, hemisphere)
- Calculating combined surface area and volume for composite solids
- Conversion of one solid shape into another
- Problems on frustum of a cone
2. How do the NCERT Solutions for Class 10 Maths Chapter 12 ensure accuracy in solving surface area and volume questions?
NCERT Solutions apply formulas systematically, provide stepwise calculations, and clarify unit conversions. Diagrams are often used to help visualize 3D shapes, and all answers adhere strictly to the latest CBSE exam pattern for Class 10 Maths.
3. What common mistakes should students avoid when solving problems from Chapter 12 Surface Areas and Volumes?
Students should avoid:
- Mixing up formulas for similar shapes (e.g., using volume formula for surface area)
- Forgetting to convert all measurements to the same units before calculation
- Ignoring whether the question asks for total or curved surface area
- Not reading scenario-based questions carefully about composite solids
4. How is the combination of solids concept applied in Class 10 Maths Chapter 12 NCERT Solutions?
In combination of solids problems, students calculate the required measure (volume or surface area) for each basic shape and then add or subtract as per the specific question's composite figure. The solutions clarify which parts to include or remove, aiding clarity in approach.
5. What are the important formulas for Surface Areas and Volumes Class 10 Chapter 12 that appear in NCERT Solutions?
Key formulas include:
- Cube volume: a³
- Cuboid volume: l × b × h
- Sphere volume: (4/3)πr³
- Cylinder volume: πr²h
- Cone volume: (1/3)πr²h
- Surface Area (various shapes) and formulas for combination and frustum as per CBSE Class 10 Maths syllabus
6. Why is unit consistency crucial in NCERT Solutions for Class 10 Maths Chapter 12 questions?
Unit consistency is essential to avoid calculation errors. All measurements (length, area, volume) must use the same units before applying formulas. The solutions always highlight this check, ensuring full marks during CBSE evaluation.
7. What strategies help visualize and solve complex 3D problems in Class 10 Surface Areas and Volumes?
Drawing labelled diagrams for each question, clearly marking dimensions, and identifying the shapes involved, helps break down the problem. The solutions guide students in mapping textual data to real figures for better comprehension.
8. How can students distinguish between surface area and volume in NCERT Class 10 Maths Chapter 12?
Surface area measures the external covering of a solid, calculated in square units (cm², m²), while volume is the space a solid occupies, measured in cubic units (cm³, m³). NCERT Solutions include explicit examples to help reinforce this distinction with various 3D shapes.
9. In what ways are composite shapes handled in NCERT Solutions for Class 10 Maths Chapter 12?
The solutions first separate each basic shape (cylinder, cone, hemisphere, etc.) forming the composite, calculate their respective volumes or surface areas, then use addition or subtraction as the scenario instructs, matching the latest CBSE problem-solving approach.
10. Are the NCERT Solutions for Chapter 12 Surface Areas and Volumes sufficient for CBSE Board preparation?
Yes, the NCERT Solutions address every exercise problem as per CBSE 2025–26 syllabus, reinforce conceptual clarity, and are recommended by teachers and top scorers for complete board exam preparation.
11. What is the process to solve frustum-related questions in NCERT Solutions for Class 10 Maths Chapter 12?
For frustums, the solutions use specific formulas for volume and surface area of a frustum of a cone and substitute given values from the question stepwise. Formula memorization and understanding shape structure are both emphasized in the explanations.
12. How does Chapter 12 link to real-world applications as per NCERT Solutions?
Chapter 12 connects 3D geometry to daily life, such as calculating paint needed for a tank, volume of containers, or surface area for wrapping. The solutions often relate questions to practical examples, enhancing understanding and applicability.
13. How should students approach word problems in NCERT Solutions for Class 10 Maths Chapter 12?
Students should:
- Identify all shapes and measurements from the problem statement
- Sketch diagrams if possible
- Select and apply correct formulas
- Check for required final units before stating the answer
14. What conceptual understanding is tested by HOTS questions in Surface Areas and Volumes?
Higher Order Thinking Skills (HOTS) questions test ability to:
- Analyze and decompose complex composite solids
- Apply formulas in unconventional ways
- Reason out conversions (e.g., melting and recasting solids)
- Justify or verify correctness of real-world numerical data involving surface area and volume
15. Why is it important to study every exercise, not just selective questions, in NCERT Solutions for Class 10 Maths Chapter 12?
Every exercise targets a different aspect of surface area and volume—from simple computation to word problems, HOTS, and real-life context. Studying all exercises ensures comprehensive understanding, which is essential for excelling in CBSE Class 10 board exams.




















 Watch Video
Watch Video