NCERT Solutions for Class 10 Maths Chapter 7 Geometry Ex 7.2

Exercise-7.2

1. Find the coordinates of the point which divides the join of \[{\text{( - 1,7)}}\] and \[{\text{(4, - 3)}}\]in the ratio \[{\text{2:3}}\]

 Ans: Let P\[{\text{(x,y)}}\] be the required point.

Let A\[{\text{( - 1,7)}}\] and B\[{\text{(4, - 3)}}\] where \[{{\text{x}}_{\text{1}}}{\text{ =  - 1,}}{{\text{y}}_{\text{1}}}{\text{ = 7,}}{{\text{x}}_{\text{2}}}{\text{ = 4,}}{{\text{y}}_{\text{2}}}{\text{ =  - 3}}\] and \[{\text{m:n = 2:3}}\]

So, by section formula

\[{\text{P(x,y)}}\]= \[\left[ {\dfrac{{{\text{m}}{{\text{x}}_{\text{2}}}{\text{ +  n}}{{\text{x}}_{\text{1}}}}}{{{\text{m  +  n}}}}{\text{,}}\dfrac{{{\text{m}}{{\text{y}}_{\text{2}}}{\text{ +  n}}{{\text{y}}_{\text{1}}}}}{{{\text{m  +  n}}}}} \right]\]

Now, substituting the values we get,

\[{\text{x  =  }}\left[ {\dfrac{{{\text{2(4)  +  3( - 1)}}}}{{{\text{2  +  3}}}}} \right]{\text{ =  }}\dfrac{{{\text{8  -  3}}}}{{\text{5}}}{\text{  =  }}\dfrac{{\text{5}}}{{\text{5}}}{\text{  =  1}}\]

\[{\text{y  =  }}\left[ {\dfrac{{{\text{2( - 3) + 3(7)}}}}{{{\text{2 + 3}}}}} \right]{\text{  =  }}\dfrac{{{\text{ - 6  +  21}}}}{{\text{5}}}{\text{  = }}\dfrac{{{\text{15}}}}{{\text{5}}}{\text{  =  3}}\]

Therefore, the co-ordinates of point P are\[{\text{(1,3)}}\]

2. Find the coordinates of the points of trisection of the line segment joining\[{\text{(4, - 1)}}\] and\[{\text{( - 2, - 3)}}\]

 Ans: 

Let line segment joining the points be A\[{\text{(4, - 1)}}\]  and B\[{\text{( - 2, - 3)}}\].

Let P\[{\text{(}}{{\text{x}}_1}{\text{,}}{{\text{y}}_1}{\text{)}}\] and Q\[{\text{(}}{{\text{x}}_2}{\text{,}}{{\text{y}}_2}{\text{)}}\] are the points of trisection of the line segment joining the given points i.e., AP = PQ = QB 

So, by section formula

\[{\text{P(x,y)}}\]= \[\left[ {\dfrac{{{\text{m}}{{\text{x}}_{\text{2}}}{\text{ +  n}}{{\text{x}}_{\text{1}}}}}{{{\text{m  +  n}}}}{\text{,}}\dfrac{{{\text{m}}{{\text{y}}_{\text{2}}}{\text{ +  n}}{{\text{y}}_{\text{1}}}}}{{{\text{m  +  n}}}}} \right]\]

Therefore, by observation point P divides AB internally in the ratio \[{\text{1:2}}\]

Now, substituting the values we get,

\[{{\text{x}}_1}{\text{ =  }}\left[ {\dfrac{{{\text{1( - 2) + 2(4)}}}}{{1 + 2}}} \right]{\text{  =  }}\dfrac{{{\text{ -  2  +  8}}}}{3}{\text{  =  }}\dfrac{6}{3}{\text{  =  2}}\]

\[{{\text{y}}_1}{\text{ =  }}\left[ {\dfrac{{{\text{1( - 3) + 2( - 1)}}}}{{{\text{1 + 2}}}}} \right]{\text{  =  }}\dfrac{{{\text{ - 3 - 2}}}}{3}{\text{  =  }}\dfrac{{{\text{ - 5}}}}{3}\]

Therefore, P\[{\text{(}}{{\text{x}}_1}{\text{,}}{{\text{y}}_1}{\text{)}}\]=\[{\text{(2, - }}\dfrac{{\text{5}}}{{\text{3}}}{\text{)}}\]

Therefore, by observation point Q divides AB internally in the ratio \[{\text{2:1}}\]

Now, substituting the values we get,

\[{{\text{x}}_1}{\text{ = }}\left[ {\dfrac{{{\text{2( - 2) + 1(4)}}}}{{2 + 1}}} \right]{\text{  =  }}\dfrac{{{\text{ - 4 + 4}}}}{3}{\text{  =  }}\dfrac{0}{3}{\text{  =  0}}\]

\[{{\text{y}}_1}{\text{ =  }}\left[ {\dfrac{{{\text{2( - 3) + 1( - 1)}}}}{{2 + 1}}} \right]{\text{ = }}\dfrac{{{\text{ - 6 - 1}}}}{3}{\text{ = }}\dfrac{{{\text{ - 7}}}}{3}\]

Therefore, Q\[{\text{(}}{{\text{x}}_2}{\text{,}}{{\text{y}}_2}{\text{)}}\]= \[{\text{(0, - }}\dfrac{7}{{\text{3}}}{\text{)}}\]

3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of \[{\text{1 m}}\]each. \[{\text{100}}\] flower pots have been placed at a distance of\[{\text{1 m}}\]from each other along AD, as shown in the following figure. Niharika runs\[\dfrac{{\text{1}}}{{\text{4}}}{\text{th}}\] the distance AD on the 2nd line and posts a green flag. Preet runs\[\dfrac{{\text{1}}}{5}{\text{th}}\] the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segments joining the two flags, where should she post her flag?

Ans: By observation, that Niharika posted the green flag at of the distance P i.e., \[{\text{(}}\dfrac{{\text{1}}}{{\text{4}}}{ \times\text{ 100)}}\;{\text{m = 25}}\;{\text{m}}\]  from the starting point of 2nd line. Therefore, the coordinates of this point P is\[{\text{(2,25)}}\]

Similarly, Preet posted red flag at of the distance Q i.e., \[{\text{(}}\dfrac{{\text{1}}}{5}{ \times \text{100)}}\;{\text{m = 20}}\;{\text{m}}\]     from the starting point of 8th line. Therefore, the coordinates of this point Q are\[{\text{(8,20)}}\]

We know that the distance between the two points is given by the distance formula

i.e. \[\sqrt {{{{\text{(}}{{\text{x}}_{\text{1}}}{\text{ - }}{{\text{x}}_{\text{2}}}{\text{)}}}^{\text{2}}}{\text{  +  (}}{{\text{y}}_{\text{1}}}{\text{ - }}{{\text{y}}_{\text{2}}}{{\text{)}}^{\text{2}}}} \]

To find the distance between these flags PQ by substituting the values we get,

PQ =\[\sqrt {{{{\text{(8 - 2)}}}^{\text{2}}}{\text{ +  (25 - 20}}{{\text{)}}^{\text{2}}}} {\text{ =  }}\sqrt {{\text{36  +  25}}} {\text{   =  }}\sqrt {{\text{61}}} \;{\text{m}}\]

The point at which Rashmi should post her blue flag is the mid-point of the line joining these points. Let this point be M\[{\text{(x,y)}}\]

So, by section formula

M\[{\text{(x,y)}}\]= \[\left[ {\dfrac{{{\text{m}}{{\text{x}}_{\text{2}}}{\text{ +  n}}{{\text{x}}_{\text{1}}}}}{{{\text{m  +  n}}}}{\text{,}}\dfrac{{{\text{m}}{{\text{y}}_{\text{2}}}{\text{ +  n}}{{\text{y}}_{\text{1}}}}}{{{\text{m  +  n}}}}} \right]\]

Now, substituting the values we get,

\[{\text{x = }}\dfrac{{{\text{2 + 8}}}}{2}{\text{ = }}\dfrac{{10}}{2}{\text{ = 5}}\]

\[{\text{y = }}\dfrac{{25 + 20}}{2}{\text{ = }}\dfrac{{{\text{45}}}}{2}{\text{ =  22}}{\text{.5}}\]

Therefore, Rashmi should post her blue flag at \[{\text{22}}{\text{.5 m}}\] on fifth line.

4. Find the ratio in which the line segment joining the points \[{\text{( - 3,10)}}\] and \[{\text{(6, - 8)}}\] is divided by \[{\text{( - 1,6)}}\].

 Ans:

Let the ratio in which the line segment joining A\[{\text{( - 3,10)}}\] and B\[{\text{(6, - 8)}}\] is divided by point P\[{\text{( - 1,6)}}\] be \[{\text{k:1}}\].

So, by section formula

M\[{\text{(x,y)}}\]= \[\left[ {\dfrac{{{\text{m}}{{\text{x}}_{\text{2}}}{\text{ +  n}}{{\text{x}}_{\text{1}}}}}{{{\text{m  +  n}}}}{\text{,}}\dfrac{{{\text{m}}{{\text{y}}_{\text{2}}}{\text{ +  n}}{{\text{y}}_{\text{1}}}}}{{{\text{m  +  n}}}}} \right]\]

\[\therefore \;{\text{ - 1 = }}\dfrac{{{\text{6k - 3}}}}{{{\text{k + 1}}}}\]

\[{\text{ - k - 1 = 6k - 3}}\]

\[{\text{7k = 2}}\]                             (by cross multiplying and transposing)

\[{\text{k = }}\dfrac{2}{7}\]

Hence the point P divides AB in the ratio\[2:7\]

5. Find the ratio in which the line segment joining A \[(1, - 5)\] and B \[( - 4,5)\] is divided by the x-axis. Also find the coordinates of the point of division.

 Ans:

 Let the ratio be \[{\text{k:1}}\]and let the line segment joining A\[(1, - 5)\] and B\[( - 4,5)\]

So, by section formula

M\[{\text{(x,y)}}\]= \[\left[ {\dfrac{{{\text{m}}{{\text{x}}_{\text{2}}}{\text{ +  n}}{{\text{x}}_{\text{1}}}}}{{{\text{m  +  n}}}}{\text{,}}\dfrac{{{\text{m}}{{\text{y}}_{\text{2}}}{\text{ +  n}}{{\text{y}}_{\text{1}}}}}{{{\text{m  +  n}}}}} \right]\]

Now, by substituting the values we get the coordinate of the point of division \[{\text{[}}\dfrac{{{\text{ - 4k + 1}}}}{{{\text{k + 1}}}}{\text{,}}\dfrac{{{\text{5k - 5}}}}{{{\text{k + 1}}}}{\text{]}}\]

We know that y-coordinate of any point on x-axis is \[{\text{0}}\] \[\therefore {\text{ }}\dfrac{{{\text{5k - 5}}}}{{{\text{k + 1}}}} = 0 \Rightarrow {\text{5k}} - 5 = 0 \Rightarrow {\text{5k}} = 5 \Rightarrow {\text{k}} = 1\]

Therefore, x-axis divides it in the ratio \[1:1\]

Division point = \[{\text{(}}\dfrac{{{\text{ - 4(1) + 1}}}}{{{\text{1 + 1}}}}{\text{,}}\dfrac{{{\text{5(1) + 5}}}}{{{\text{1 + 1}}}}{\text{) = (}}\dfrac{{{\text{ - 4 + 1}}}}{{\text{2}}}{\text{,}}\dfrac{{{\text{5 + 5}}}}{{\text{2}}}{\text{) = (}}\dfrac{{{\text{ - 3}}}}{{\text{2}}}{\text{,0)}}\]

6. If \[{\text{(1,2)}}\], \[{\text{(4,y)}}\], \[{\text{(x,6)}}\] and \[{\text{(3,5)}}\] are the vertices of a parallelogram taken in order, find \[{\text{x}}\]and \[{\text{y}}\]

 Ans: 

Let A\[{\text{(1,2)}}\], B\[{\text{(4, y)}}\],C\[{\text{(x,6)}}\] and D\[{\text{(3,5)}}\] are the vertices of a parallelogram ABCD. Since the diagonals of a parallelogram bisect each other, Intersection point O of diagonal AC and BD also divides these diagonals Therefore, O is the mid-point of AC and BD. 

If O is the mid-point of AC, then the coordinates of O are

\[{\text{(}}\dfrac{{{\text{1 + x}}}}{{\text{2}}}{\text{,}}\dfrac{{{\text{2 + 6}}}}{{\text{2}}}{\text{)}} \Rightarrow {\text{(}}\dfrac{{{\text{x + 1}}}}{{\text{2}}}{\text{,4)}}\]

If O is the mid-point of BD, then the coordinates of O are\[{\text{(}}\dfrac{{{\text{4 + 3}}}}{{\text{2}}}{\text{,}}\dfrac{{{\text{5 + y}}}}{{\text{2}}}{\text{)}} \Rightarrow {\text{(}}\dfrac{{\text{7}}}{{\text{2}}}{\text{,}}\dfrac{{{\text{5 + y}}}}{{\text{2}}}{\text{)}}\]

Since both the coordinates are of the same point O, \[\dfrac{{{\text{1 + x}}}}{{\text{2}}}{\text{ = }}\dfrac{{\text{7}}}{{\text{2}}}\;{\text{and}}\;\dfrac{{{\text{5 + y}}}}{{\text{2}}}{\text{ = 4}}\]

\[{\text{x  + 1  =  7}}\;{\text{and}}\;{\text{5  +  y  =  8}}\]

\[{\text{x  =  6}}\;{\text{and}}\;{\text{y  =  3}}\]

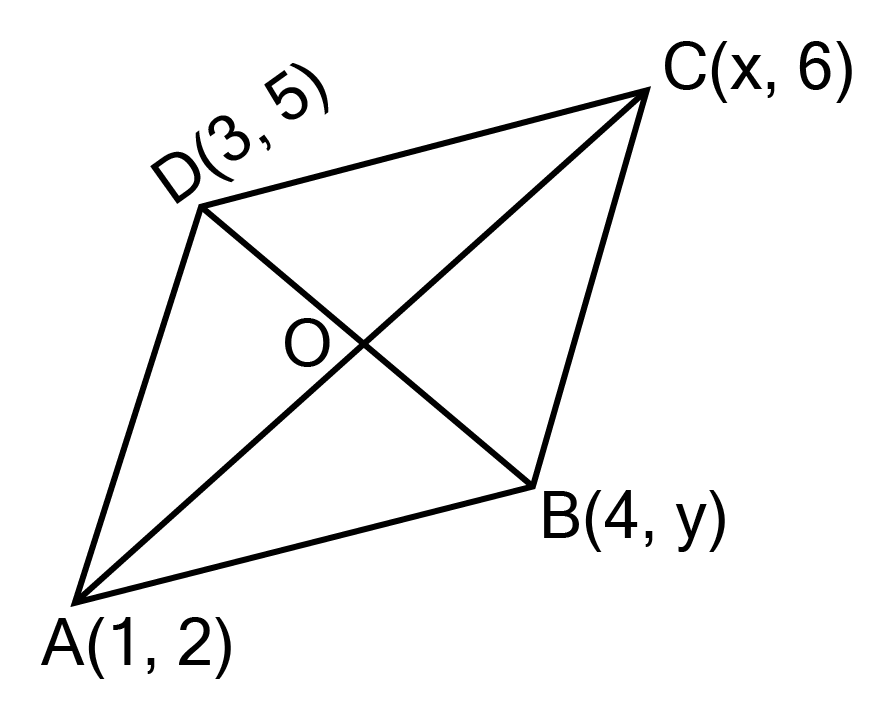
7. Find the coordinates of a point A, where AB is the diameter of circle whose centre is\[{\text{(2, - 3)}}\] and B is\[{\text{(1,4)}}\]

 Ans: 

Let the coordinates of point A be\[{\text{(x,y)}}\] 

Mid-point of AB is C\[{\text{(2, - 3)}}\], which is the center of the circle.

\[{\text{(2, - 3) = (}}\dfrac{{{\text{x + 1}}}}{{\text{2}}}{\text{,}}\dfrac{{{\text{y + 4}}}}{{\text{2}}}{\text{)}}\]

\[\dfrac{{{\text{x + 1}}}}{{\text{2}}}{\text{ = 2 and}}\;\dfrac{{{\text{y + 4}}}}{{\text{2}}} =  - 3\]

\[{\text{x  +  1 =  4  and}}\;{\text{y  +  4  =   - 6  }}\]

\[{\text{x = 3 and}}\;{\text{y =  - 10}}\]. 

So, coordinates of A are \[{\text{(3, - 10)}}\]

8. If A and B are\[{\text{( - 2, - 2)}}\] and\[{\text{(2, - 4)}}\] respectively, find the coordinates of P such that\[{\text{AP = }}\dfrac{{\text{3}}}{{\text{7}}}{\text{AB}}\] and P lies on the line segment AB.

 Ans: 

The coordinates of point A and B are\[{\text{( - 2, - 2)}}\] and\[{\text{(2, - 4)}}\] respectively and \[{\text{AP = }}\dfrac{{\text{3}}}{{\text{7}}}{\text{AB}}\] so, \[\dfrac{{{\text{AP}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{\text{3}}}{{\text{7}}}\]

We know that AB = AP + PB from figure, 

\[\dfrac{{{\text{AP + PB}}}}{{{\text{AP}}}}{\text{ = }}\dfrac{{{\text{3 + 4}}}}{3}\]

\[1 + \dfrac{{{\text{PB}}}}{{{\text{AP}}}}{\text{ = 1 + }}\dfrac{{\text{4}}}{3}\]

\[\dfrac{{{\text{PB}}}}{{{\text{AP}}}}{\text{ = }}\dfrac{{\text{4}}}{3}\]

Therefore, \[{\text{PB:AP = 4:3}}\]

Point P\[{\text{(x,y)}}\] divides the line segment AB in the ratio\[{\text{3:4}}\]

Coordinates of P\[{\text{(x,y)}}\] = \[{\text{(}}\dfrac{{{\text{3 * 2 + 4 * ( - 2)}}}}{{{\text{3 + 4}}}}{\text{,}}\dfrac{{{\text{3 * ( - 4) + 4 * ( - 2)}}}}{{{\text{3 + 4}}}}{\text{)}}\]

                                           = \[{\text{(}}\dfrac{{{\text{6 - 8}}}}{{\text{7}}}{\text{,}}\dfrac{{{\text{ - 12 - 8}}}}{{\text{7}}}{\text{)}}\;{\text{ = }}\;{\text{(}}\dfrac{{{\text{ - 2}}}}{{\text{7}}}{\text{,}}\dfrac{{{\text{ - 20}}}}{{\text{7}}}{\text{)}}\]

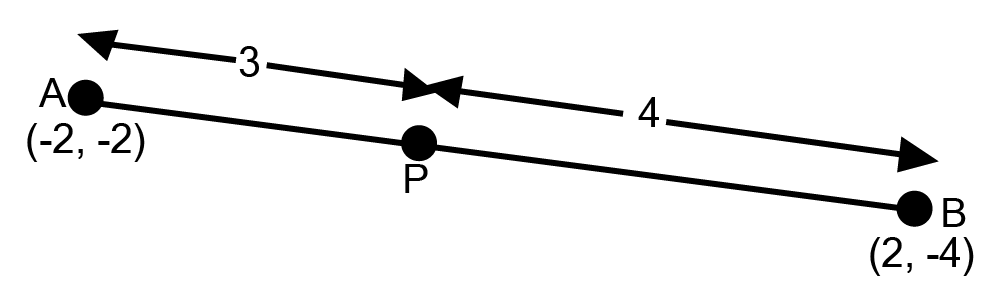
9. Find the coordinates of the points which divide the line segment joining A\[{\text{( - 2,2)}}\] and B\[{\text{(2,8)}}\] into four equal parts.

 Ans:

By observation, \[{{\text{P}}_1}\],\[{{\text{P}}_2}\],\[{{\text{P}}_3}\] that points divides the line segment A\[{\text{( - 2,2)}}\]and B\[{\text{(2,8)}}\]into four equal parts. Point\[{{\text{P}}_1}\] divides the line segment A\[{{\text{P}}_2}\] into two equal parts 

Hence, Coordinates of \[{{\text{P}}_1}\]= \[(\dfrac{{1 \times 2 + 3 \times ( - 2)}}{{1 + 3}},\dfrac{{1 \times 8 + 3 \times 2}}{{1 + 3}})\; = \;( - 1,\dfrac{7}{2})\]

Point\[{{\text{P}}_2}\] divides the line segment AB into two equal parts

Coordinates of \[{{\text{P}}_2}\]= \[(\dfrac{{2 + ( - 2)}}{2},\dfrac{{2 + 8}}{2})\; = \;(0,5)\]

Point \[{{\text{P}}_{\text{3}}}\] divides the line segment B \[{{\text{P}}_2}\] into two equal parts

Coordinates of \[{{\text{P}}_3}\]= \[(\dfrac{{3 \times 2 + 1 \times ( - 2)}}{{1 + 3}},\dfrac{{3 \times 8 + 1 \times 2}}{{1 + 3}})\; = \;(1,\dfrac{{13}}{2})\]

10. Find the area of a rhombus if its vertices are \[{\text{(3,0)}}\], \[{\text{(4,5)}}\], \[{\text{( - 1,4)}}\] and \[{\text{( - 2, - 1)}}\] taken in order. \[\text{ [Hint: Area of a rhombus = (product of its diagonals)]}\]

 Ans: 

Let A\[{\text{(3,0)}}\],B\[{\text{(4,5)}}\],C\[{\text{( - 1,4)}}\] and D\[{\text{( - 2, - 1)}}\] are the vertices of a rhombus ABCD. 

We know that the distance between the two points is given by the distance formula

i.e. \[\sqrt {{{{\text{(}}{{\text{x}}_{\text{1}}}{\text{ - }}{{\text{x}}_{\text{2}}}{\text{)}}}^{\text{2}}}{\text{ + (}}{{\text{y}}_{\text{1}}}{\text{ - }}{{\text{y}}_{\text{2}}}{{\text{)}}^{\text{2}}}} \]

Therefore, distance between A\[{\text{(3,0)}}\]and C\[{\text{( - 1,4)}}\] is given by

Length of diagonal AC = \[\sqrt {{{[3 - ( - 1)]}^2} + {{(0 - 4)}^2}}  = \sqrt {16 + 16}  = 4\sqrt 2 \]

Therefore, distance between B\[{\text{(4,5)}}\]and D \[{\text{( - 2, - 1)}}\] is given by

Length of diagonal BD = \[\sqrt {{{[4 - ( - 2)]}^2} + {{(5 - ( - 1))}^2}}  = \sqrt {36 + 36}  = 6\sqrt 2 \]

Area of rhombus ABCD = \[\dfrac{{\text{1}}}{{\text{2}}} \times{\text{ (product}}\;{\text{of}}\;{\text{lengths}}\;{\text{of}}\;{\text{diagonals)}}\]

                                      = \[\dfrac{{\text{1}}}{{\text{2}}}{\text{ AC}} \times {\text{BD}}\]

                                      = \[\dfrac{{\text{1}}}{{\text{2}}} \times{\text{ 4}}\sqrt {\text{2}}  \times{\text{6}}\sqrt {\text{2}} {\text{ = 24}}\;{\text{square}}\;{\text{units}}\]

Conclusion

The NCERT Solutions for class 10 maths chapter 7 exercise 7.2 on Coordinate Geometry, provided by Vedantu, offer comprehensive explanations and step-by-step solutions to all problems in this exercise. This chapter is crucial as it deals with key concepts such as finding the distance between two points, determining the coordinates of a point dividing a line segment in a given ratio, and calculating the area of a triangle using coordinate geometry. Practising these problems will build a strong foundation in coordinate geometry, which is beneficial for higher studies as well.

NCERT Solutions for Class 10 Maths Chapter 7 all Other Exercises

CBSE Class 10 Maths Chapter 7 Other Study Materials

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.