
Solving Coordinate Geometry Problems in Class 10 Maths Chapter 7
Class 10 Maths Chapter 7 Coordinate Geometry introduces students to solving problems using the distance formula on a coordinate plane. Many learners find it challenging to correctly plot points and apply formulas, especially when questions involve real-life situations. Using NCERT solutions helps students understand the correct method and logical flow required to solve such problems.
 Table of Content
Table of ContentThe Coordinate Geometry Class 10 solutions explain how to locate points on the Cartesian plane and calculate distances between them step by step. Each solution follows the NCERT approach, ensuring that calculations, formula application, and final answers are presented clearly and neatly — exactly as expected in board exams.
By practising NCERT Solutions for Class 10 Maths Chapter 7, students can reduce calculation errors and improve accuracy. Regular revision of these solutions builds confidence and makes it easier to handle coordinate-based questions in school exams as well as the CBSE Class 10 board examination.
Access Exercise Wise NCERT Solutions for Chapter 7 Maths Class 10
S. No | Current Syllabus Exercises of Class 10 Maths Chapter 7 |
1 | NCERT Solutions of Class 10 Maths Coordinate Geometry Exercise 7.1 |
2 | NCERT Solutions of Class 10 Maths Coordinate Geometry Exercise 7.2 |
Class 10 Maths Chapter 7 Coordinate Geometry NCERT Solution



Find All Coordinate Geometry Class 10 Questions and Answers Here
NCERT Solutions for Chapter 7 Class 10 Maths, "Coordinate Geometry" covers the following four exercises:
Exercise 7.1 - This exercise contains 10 questions, students are introduced to the concept of the Cartesian Plane, plotting points on the plane, and finding the coordinates of a point. Students learn how to identify the quadrants of the plane and the axes (x-axis and y-axis). The exercise contains questions related to finding the coordinates of a point, plotting a point on the plane, and identifying the quadrant in which a point lies.
Exercise 7.2 - This exercise contains 10 questions, students learn to find the distance between two points on a Cartesian Plane using the distance formula. They are also taught how to apply the midpoint formula to find the midpoint of a line segment. This exercise contains questions related to finding the distance between two points, finding the midpoint of a line segment, and applying the distance and midpoint formulas to solve problems.
Access NCERT Solutions for Class 10 Maths Chapter 7 - Coordinate Geometry Exercise 7.1
1. Find the distance between the following pairs of points:
(i) $\left( 2,3 \right),\left( 4,1 \right)$
Ans:
Given that,
Let the points be $\left( 2,3 \right)$ and $\left( 4,1 \right)$
To find the distance between the points $\left( 2,3 \right),\left( 4,1 \right)$.
Distance between two points is given by the Distance formula $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Here, ${{x}_{1}}=2$
${{x}_{2}}=4$
${{y}_{1}}=3$
${{y}_{2}}=1$
Thus, the distance between $\left( 2,3 \right)$ and $\left( 4,1 \right)$ is given by,
$d=\sqrt{{{\left( 2-4 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}}$
$=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 2 \right)}^{2}}}$
$=\sqrt{4+4}$
$=\sqrt{8}$
$=2\sqrt{2}$
$\therefore $The distance between $\left( 2,3 \right)$ and $\left( 4,1 \right)$ is $2\sqrt{2}$ units.
(ii) $\left( -5,7 \right),\left( -1,3 \right)$
Ans:
Given that,
Let the points be $\left( -5,7 \right)$ and $\left( -1,3 \right)$
To find the distance between the points $\left( -5,7 \right),\left( -1,3 \right)$.
Distance between two points is given by the Distance formula $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Here, ${{x}_{1}}=-5$
${{x}_{2}}=-1$
${{y}_{1}}=7$
${{y}_{2}}=3$
Thus, the distance between $\left( -5,7 \right)$ and $\left( -1,3 \right)$ is given by,
$d=\sqrt{{{\left( -5-\left( -1 \right) \right)}^{2}}+{{\left( 7-3 \right)}^{2}}}$
$=\sqrt{{{\left( -4 \right)}^{2}}+{{\left( 4 \right)}^{2}}}$
$=\sqrt{16+16}$
$=\sqrt{32}$
$=4\sqrt{2}$
$\therefore $The distance between $\left( -5,7 \right)$ and $\left( -1,3 \right)$ is $4\sqrt{2}$ units.
(iii) $\left( a,b \right),\left( -a,-b \right)$
Ans:
Given that,
Let the points be $\left( a,b \right)$ and $\left( -a,-b \right)$
To find the distance between the points $\left( a,b \right),\left( -a,-b \right)$.
Distance between two points is given by the Distance formula $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Here, ${{x}_{1}}=a$
${{x}_{2}}=-a$
${{y}_{1}}=b$
${{y}_{2}}=-b$
Thus, the distance between $\left( a,b \right)$ and $\left( -a,-b \right)$ is given by,
$d=\sqrt{{{\left( a-\left( -a \right) \right)}^{2}}+{{\left( b-\left( -b \right) \right)}^{2}}}$
$=\sqrt{{{\left( 2a \right)}^{2}}+{{\left( 2b \right)}^{2}}}$
$=\sqrt{4{{a}^{2}}+4{{b}^{2}}}$
$=\sqrt{4}\sqrt{{{a}^{2}}+{{b}^{2}}}$
$=2\sqrt{{{a}^{2}}+{{b}^{2}}}$
$\therefore $The distance between $\left( a,b \right)$ and $\left( -a,-b \right)$ is $2\sqrt{{{a}^{2}}+{{b}^{2}}}$ units.
2. Find the distance between the points $\left( 0,0 \right)$ and $\left( 36,15 \right)$. Can you now find the distance between the two towns $A$ and $B$ discussed in Section 7.2?
Ans:
Given that,
Let the points be $\left( 0,0 \right)$ and $\left( 36,15 \right)$
To find the distance between the points $\left( 0,0 \right),\left( 36,15 \right)$.
Distance between two points is given by the Distance formula $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Here, ${{x}_{1}}=0$
${{x}_{2}}=36$
${{y}_{1}}=0$
${{y}_{2}}=15$
Thus, the distance between $\left( 0,0 \right)$ and $\left( 36,15 \right)$ is given by,
$d=\sqrt{{{\left( 0-36 \right)}^{2}}+{{\left( 0-15 \right)}^{2}}}$
$=\sqrt{{{\left( -36 \right)}^{2}}+{{\left( -15 \right)}^{2}}}$
$=\sqrt{1296+225}$
$=\sqrt{1521}$
$=39$
Yes, it is possible to find the distance between the given towns $A$ and $B$. The positions of this town are $A\left( 0,0 \right)$ and $B\left( 36,15 \right)$. And it can be calculated as above.
$\therefore $The distance between $A\left( 0,0 \right)$ and $B\left( 36,15 \right)$ is $39$ km.
3. Determine if the points $\left( 1,5 \right),\left( 2,3 \right)$ and $\left( -2,-11 \right)$ are collinear.
Ans:
Given that,
Let the three points be $\left( 1,5 \right),\left( 2,3 \right)$ and $\left( -2,-11 \right)$
To determine if the given points are collinear
Let $A\left( 1,5 \right),B\left( 2,3 \right),C\left( -2,-11 \right)$ be the vertices of the given triangle.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $A\left( 1,5 \right)$ and $B\left( 2,3 \right)$
${{x}_{1}}=1$
${{x}_{2}}=2$
${{y}_{1}}=5$
${{y}_{2}}=3$
$AB=\sqrt{{{\left( 1-2 \right)}^{2}}+{{\left( 5-3 \right)}^{2}}}$
$=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( 2 \right)}^{2}}}$
$=\sqrt{1+4}$
$=\sqrt{5}$
To find the distance between the points $B\left( 2,3 \right)$ and $C\left( -2,-11 \right)$
${{x}_{1}}=2$
${{x}_{2}}=-2$
${{y}_{1}}=3$
${{y}_{2}}=-11$
$BC=\sqrt{{{\left( 2-\left( -2 \right) \right)}^{2}}+{{\left( 3-\left( -11 \right) \right)}^{2}}}$
$=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( 14 \right)}^{2}}}$
$=\sqrt{16+196}$
$=\sqrt{212}$
To find the distance between the points $A\left( 1,5 \right)$ and $C\left( -2,-11 \right)$
${{x}_{1}}=1$
${{x}_{2}}=-2$
${{y}_{1}}=5$
${{y}_{2}}=-11$
$CA=\sqrt{{{\left( 1-\left( -2 \right) \right)}^{2}}+{{\left( 5-\left( -11 \right) \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 16 \right)}^{2}}}$
$=\sqrt{9+256}$
$=\sqrt{265}$
Since $AB+AC\ne BC$ and $AB\ne BC+AC$
and $AC\ne BC$
$\therefore $The points $A\left( 1,5 \right),B\left( 2,3 \right),C\left( -2,-11 \right)$ are not collinear.
4. Check whether $\left( 5,-2 \right),\left( 6,4 \right)$ and $\left( 7,-2 \right)$ are the vertices of an isosceles triangle.
Ans:
Given that,
Let the three points be $\left( 5,-2 \right),\left( 6,4 \right)$ and $\left( 7,-2 \right)$ are the vertices of the triangle.
To determine if the given points are the vertices of an isosceles triangle.
Let $A\left( 5,-2 \right),B\left( 6,4 \right),C\left( 7,-2 \right)$ be the vertices of the given triangle.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $A\left( 5,-2 \right)$ and $B\left( 6,4 \right)$
${{x}_{1}}=5$
${{x}_{2}}=6$
${{y}_{1}}=-2$
${{y}_{2}}=4$
$AB=\sqrt{{{\left( 5-6 \right)}^{2}}+{{\left( -2-4 \right)}^{2}}}$
$=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -6 \right)}^{2}}}$
$=\sqrt{1+36}$
$=\sqrt{37}$
To find the distance between the points $B\left( 6,4 \right)$ and $C\left( 7,-2 \right)$
${{x}_{1}}=6$
${{x}_{2}}=7$
${{y}_{1}}=4$
${{y}_{2}}=-2$
$BC=\sqrt{{{\left( 6-7 \right)}^{2}}+{{\left( 4-\left( -2 \right) \right)}^{2}}}$
$=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( 6 \right)}^{2}}}$
$=\sqrt{1+36}$
$=\sqrt{37}$
To find the distance between the points $A\left( 5,-2 \right)$ and $C\left( 7,-2 \right)$
${{x}_{1}}=5$
${{x}_{2}}=7$
${{y}_{1}}=-2$
${{y}_{2}}=-2$
$CA=\sqrt{{{\left( 5-7 \right)}^{2}}+{{\left( -2-\left( -2 \right) \right)}^{2}}}$
$=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 0 \right)}^{2}}}$
$=\sqrt{4+0}$
$=2$
We can conclude that $AB=BC$.
Since two sides of the triangle are equal in length, $ABC$ is an isosceles triangle.
5. In a classroom, $4$ friends are seated at the points $A,B,C$ and $D$ are shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think $ABCD$ is a square?” Chameli disagrees.
Using the distance formula, find which of them is correct.
Ans:
Given that,
$4$ friends are seated at the points $A,B,C,D$
To find,
If they form square together by using distance formula
From the figure, we observe the points $A\left( 3,4 \right),B\left( 6,7 \right),C\left( 9,4 \right)$ and $D\left( 6,1 \right)$ are the positions of the four students.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $A\left( 3,4 \right)$ and $B\left( 6,7 \right)$
${{x}_{1}}=3$
${{x}_{2}}=6$
${{y}_{1}}=4$
${{y}_{2}}=7$
$AB=\sqrt{{{\left( 3-6 \right)}^{2}}+{{\left( 4-7 \right)}^{2}}}$
$=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( -3 \right)}^{2}}}$
$=\sqrt{9+9}$
$=\sqrt{18}$
$=3\sqrt{2}$
To find the distance between the points $B\left( 6,7 \right)$ and $C\left( 9,4 \right)$
${{x}_{1}}=6$
${{x}_{2}}=9$
${{y}_{1}}=7$
${{y}_{2}}=4$
$BC=\sqrt{{{\left( 6-9 \right)}^{2}}+{{\left( 7-4 \right)}^{2}}}$
$=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 3 \right)}^{2}}}$
$=\sqrt{9+9}$
$=\sqrt{18}$
$=3\sqrt{2}$
To find the distance between the points $C\left( 9,4 \right)$ and $\left( 6,1 \right)$
${{x}_{1}}=9$
${{x}_{2}}=6$
${{y}_{1}}=4$
$=2\left( lb+bh+lh \right)$
\[\]
$=2\left( 80 \right)CD=\sqrt{{{\left( 9-6 \right)}^{2}}+{{\left( 4-1 \right)}^{2}}}$
$\therefore =\sqrt{9+9}$
$=\sqrt{18}$
$=3\sqrt{2}$
To find the distance between the points $A\left( 3,4 \right)$ and $D\left( 6,1 \right)$
${{x}_{1}}=3$
${{x}_{2}}=6$
${{y}_{1}}=4$
${{y}_{2}}=1$
$AB=\sqrt{{{\left( 3-6 \right)}^{2}}+{{\left( 4-1 \right)}^{2}}}$
$=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 3 \right)}^{2}}}$
$=\sqrt{9+9}$
$=\sqrt{18}$
$=3\sqrt{2}$
Since all sides of the squares are equal, now find the distance between the diagonals $AC$ and $BD$.
To find the distance between the points $A\left( 3,4 \right)$ and $C\left( 9,4 \right)$
$=13\text{ cm}{{x}_{1}}=3$
${{x}_{2}}=9$
${{y}_{1}}=4$
${{y}_{2}}=4$
Diagonal $AC=\sqrt{{{\left( 3-9 \right)}^{2}}+{{\left( 4-4 \right)}^{2}}}$
$=\sqrt{{{\left( -6 \right)}^{2}}+{{\left( 0 \right)}^{2}}}$
$=\sqrt{36+0}$
$=6$
Diagonal To find the distance between the points $B\left( 6,7 \right)$ and $D\left( 6,1 \right)$
${{x}_{1}}=6$
${{x}_{2}}=6$
${{y}_{1}}=7$
${{y}_{2}}=1$
Diagonal $BD=\sqrt{{{\left( 6-6 \right)}^{2}}+{{\left( 7-1 \right)}^{2}}}$
$=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( 6 \right)}^{2}}}$
$=\sqrt{0+36}$
$=6$
Thus, the four sides \[\] and $DA$ are equal and its diagonals $AC$ and $BD$ are also equal.
$\therefore ABCD$ form a square and hence Champa was correct.
6. Name the type of quadrilateral forms, if any, by the following points, and give reasons for your answer.
(i) $\left( -1,-2 \right),\left( 1,0 \right),\left( -1,2 \right),\left( -3,0 \right)$-
Ans:
Given that,
Let the given points denote the vertices $A\left( -1,-2 \right),B\left( 1,0 \right),C\left( -1,2 \right),D\left( -3,0 \right)$ denote the vertices of the quadrilateral.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $A\left( -1,-2 \right)$ and $B\left( 1,0 \right)$
${{x}_{1}}=-1$
${{x}_{2}}=1$
${{y}_{1}}=-2$
${{y}_{2}}=0$
$AB=\sqrt{{{\left( -1-1 \right)}^{2}}+{{\left( -2-0 \right)}^{2}}}$
$=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( -2 \right)}^{2}}}$
$=\sqrt{4+4}$
$=3.5\text{ cm}=\sqrt{8}$
$=2\sqrt{2}$
To find the distance between the points $B\left( 1,0 \right)$ and $C\left( -1,2 \right)$
${{x}_{1}}=1$
${{x}_{2}}=-1$
${{y}_{1}}=0$
${{y}_{2}}=2$
$BC=\sqrt{{{\left( 1-\left( -1 \right) \right)}^{2}}+{{\left( 0-2 \right)}^{2}}}$
$=\sqrt{{{\left( 2 \right)}^{2}}+{{\left( -2 \right)}^{2}}}$
$=\sqrt{4+4}$
$=\sqrt{8}$
$=2\sqrt{2}$
To find the distance between the points $C\left( -1,2 \right)$ and \[\]
$=137.5{{x}_{1}}=-1$
${{x}_{2}}=-3$
${{y}_{1}}=2$
${{y}_{2}}=0$
$CD=\sqrt{{{\left( -1-\left( -3 \right) \right)}^{2}}+{{\left( 2-0 \right)}^{2}}}$
$=\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 2 \right)}^{2}}}$
$=\sqrt{4+4}$
$=\sqrt{8}$
$=2\sqrt{2}$
To find the distance between the points $D\left( -3,0 \right)$ and $A\left( -1,-2 \right)$
${{x}_{1}}=-3$
${{x}_{2}}=-1$
${{y}_{1}}=0$
${{y}_{2}}=-2$
$AD=\sqrt{{{\left( -3-\left( -1 \right) \right)}^{2}}+{{\left( 0-\left( -2 \right) \right)}^{2}}}$
$=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 2 \right)}^{2}}}$
$=\sqrt{4+4}$
$=\sqrt{8}$
$=2\sqrt{2}$
To find the diagonals of the given quadrilateral
To find the distance between the points $A\left( -1,-2 \right)$ and $C\left( -1,2 \right)$
${{x}_{1}}=-1$
${{x}_{2}}=-1$
$=l{{y}_{1}}=-2$
${{y}_{2}}=2$
Diagonal $AC=\sqrt{{{\left( -1-\left( -1 \right) \right)}^{2}}+{{\left( -2-2 \right)}^{2}}}$
$=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( -4 \right)}^{2}}}$
$=\sqrt{0+16}$
$=4$
To find the distance between the points $B\left( 1,0 \right)$ and $D\left( -3,0 \right)$
${{x}_{1}}=1$
${{x}_{2}}=-3$
${{y}_{1}}=0$
${{y}_{2}}=0$
Diagonal $BD=\sqrt{{{\left( 1-\left( -3 \right) \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}$
$=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( 0 \right)}^{2}}}$
$=\sqrt{16+0}$
$=4$
Since all sides of the given quadrilateral are of the same measure and the diagonals are also the same length.
$\therefore $The given points of the quadrilateral form a square.
(ii) $\left( -3,5 \right),\left( 3,1 \right),\left( 0,3 \right),\left( -1,-4 \right)$-
Ans:
Given that,
Let the given points denote the vertices $A\left( -3,5 \right),B\left( 3,1 \right),C\left( 0,3 \right),D\left( -1,-4 \right)$ denote the vertices of the quadrilateral.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $A\left( -3,5 \right)$ and $B\left( 3,1 \right)$
${{x}_{1}}=-3$
${{x}_{2}}=3$
${{y}_{1}}=5$
${{y}_{2}}=1$
$AB=\sqrt{{{\left( -3-3 \right)}^{2}}+{{\left( 5-1 \right)}^{2}}}$
$=\sqrt{{{\left( -6 \right)}^{2}}+{{\left( 4 \right)}^{2}}}$
$=\sqrt{36+16}$
$=\sqrt{52}$
$=2\sqrt{13}$
To find the distance between the points \[\] and $C\left( 0,3 \right)$
${{x}_{1}}=3$
${{x}_{2}}=0$
${{y}_{1}}=1$
${{y}_{2}}=3$
$BC=\sqrt{{{\left( 3-0 \right)}^{2}}+{{\left( 1-3 \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( -2 \right)}^{2}}}$
$=\sqrt{9+4}$
$=\sqrt{13}=14-5$
To find the distance between the points $C\left( 0,3 \right)=45\pi $ and $\therefore D\left( -1,-4 \right)$
${{x}_{1}}=0$
${{x}_{2}}=-1$
${{y}_{1}}=3$
${{y}_{2}}=-4$
$CD=\sqrt{{{\left( 0-\left( -1 \right) \right)}^{2}}+{{\left( 3-\left( -4 \right) \right)}^{2}}}$
$=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 7 \right)}^{2}}}$
$=\sqrt{1+49}$
$=\sqrt{50}$
$=5\sqrt{2}$
To find the distance between the points $A\left( -3,5 \right)$ and $D\left( -1,-4 \right)$
${{x}_{1}}=-344\text{ }{{\text{m}}^{2}}$
${{x}_{2}}=-1$
${{y}_{1}}=5$
${{y}_{2}}=-4$
$AD=\sqrt{{{\left( -3-\left( -1 \right) \right)}^{2}}+{{\left( 5-\left( -4 \right) \right)}^{2}}}$
$=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 9 \right)}^{2}}}$
$=\sqrt{4+81}$
$=\sqrt{85}$
From the distance we found that,
$AB\ne BC\ne CD\ne AD$
By plotting the graph, we get,
From the graph above, we can note that the points $ABC$ are collinear.
$\therefore $The quadrilateral cannot be formed by using the above points.
(iii) $\left( 4,5 \right),\left( 7,6 \right),\left( 4,3 \right),\left( 1,2 \right)$-
Ans:
Given that,
Let the given points denote the vertices $A\left( 4,5 \right),B\left( 7,6 \right),C\left( 4,3 \right),D\left( 1,2 \right)$ denote the vertices of the quadrilateral.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $A\left( 4,5 \right)$ and $B\left( 7,6 \right)$
${{x}_{1}}=4$
${{x}_{2}}=7$
${{y}_{1}}=5$
${{y}_{2}}=6$
$AB=\sqrt{{{\left( 4-7 \right)}^{2}}+{{\left( 5-6 \right)}^{2}}}$
$=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( -1 \right)}^{2}}}$
$=\sqrt{9+1}$
$=\sqrt{10}$
To find the distance between the points $B\left( 7,6 \right)$ and $C\left( 4,3 \right)$
${{x}_{1}}=7$
${{x}_{2}}=4$
${{y}_{1}}=6$
${{y}_{2}}=3$
$BC=\sqrt{{{\left( 7-4 \right)}^{2}}+{{\left( 6-3 \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 3 \right)}^{2}}}$
$=\frac{1.4}{2}=\sqrt{9+9}$
$=\sqrt{18}$
$=3\sqrt{2}$
To find the distance between the points $C\left(4,3 \right)$ and $D\left( 1,2 \right)$
${{x}_{1}}=4$
${{x}_{2}}=1$
${{y}_{1}}=3$
${{y}_{2}}=2$
$CD=\sqrt{{{\left( 4-1 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 1 \right)}^{2}}}$
$=\sqrt{9+1}$
$=\sqrt{10}$
To find the distance between the points x$A\left( 4,5 \right)$ and $D\left( 1,2 \right)$
${{x}_{1}}=4$
${{x}_{2}}=1$
${{y}_{1}}=5$
${{y}_{2}}=2$
$AD=\sqrt{{{\left( 4-1 \right)}^{2}}+{{\left( 5-2 \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 3 \right)}^{2}}}$
$=\sqrt{9+9}$
$=\sqrt{18}$
$=3\sqrt{2}$
To find the diagonals of the given quadrilateral
To find the distance between the points $A\left( 4,5 \right)$ and $C\left( 4,3 \right)$
${{x}_{1}}=4$
${{x}_{2}}=4$
${{y}_{1}}=5$
${{y}_{2}}=3$
Diagonal $AC=\sqrt{{{\left( 4-4 \right)}^{2}}+{{\left( 5-3 \right)}^{2}}}$
$=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( 2 \right)}^{2}}}$
$=\sqrt{0+4}$
$=2$
To find the distance between the points $B\left( 7,6 \right)$ and $D\left( 1,2 \right)$
${{x}_{1}}=7$
${{x}_{2}}=1$
${{y}_{1}}=6$
${{y}_{2}}=2$
Diagonal $BD=\sqrt{{{\left( 7-1 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}}$
$=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 4 \right)}^{2}}}$
$=\sqrt{36+16}$
$=\sqrt{52}$
$=2\sqrt{13}$
From the above calculation, the opposite sides of the quadrilateral are of same length and the diagonals are not of same length
$\therefore $The given points of the quadrilateral form a parallelogram.
Question 7:
Find the point on the $x$-axis which is equidistant from $\left( 2,-5 \right)$ and $\left( -2,9 \right)$.
Ans:
Given that,
$\left( 2,-5 \right)$
$\left( -2,9 \right)$
To find,
The point that is equidistant from the points $\left( 2,-5 \right)$ and $\left( -2,9 \right)$
Let us consider the points as $A\left( 2,-5 \right)$ and $B\left( -2,9 \right)$ and to find the equidistant point $P$.
Since the point is on $x$-axis, the coordinates of the required point is of the form $P\left( x,0 \right)$.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
To find the distance between the points $P\left( x,0 \right)$ and $A\left( 2,-5 \right)$
${{x}_{1}}=x$
${{x}_{2}}=2$
${{y}_{1}}=0$
${{y}_{2}}=-5$
$PA=\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( 0-\left( -5 \right) \right)}^{2}}}$
$=\sqrt{{{\left( x-2 \right)}^{2}}+25}$
To find the distance between the points $A\left( x,0 \right)$ and $B\left( -2,9 \right)$
${{x}_{1}}=x$
${{x}_{2}}=-2$
${{y}_{1}}=0$
${{y}_{2}}=9$
$PB=\sqrt{{{\left( x-\left( -2 \right) \right)}^{2}}+{{\left( 0-9 \right)}^{2}}}$
$=\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( -9 \right)}^{2}}}$
$=\sqrt{{{\left( x+2 \right)}^{2}}+81}$
Since the distance are equal in measure,
$PA=PB$
$\sqrt{{{\left( x-2 \right)}^{2}}+25}$ $=\sqrt{{{\left( x+2 \right)}^{2}}+81}$
Taking square on both sides,
${{(x-2)}^{2}}+25= ${{(x+2)}^{2}}+81
By solving, we get,
${{x}^{2}}+4-4x+25={{x}^{2}}+4+4x+81$
$8x=-56$
$x=-7$
The coordinate is $\left( -7,0 \right)$.
$\therefore $The point that is equidistant from $\left( 2,-5 \right)$ and $\left( -2,9 \right)$ is $\left( -7,0 \right)$.
8. Find the values of $y$for which the distance between the points $P\left( 2,-3 \right)$ and $Q\left( 10,y \right)$ is $10$units.
Ans:
Given that,
$P\left( 2,-3 \right)$
$Q\left( 10,y \right)$
The distance between these points is $10$ units.
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
.To find the distance between the points $P\left( 2,-3 \right)$ and $Q\left( 10,y \right)$
${{x}_{1}}=2$
${{x}_{2}}=10$
${{y}_{1}}=-3$
${{y}_{2}}=y$
$PQ=\sqrt{{{\left( 10-2 \right)}^{2}}+{{\left( y-\left( -3 \right) \right)}^{2}}}$
$=\sqrt{{{\left( -8 \right)}^{2}}+{{\left( y+3 \right)}^{2}}}$
$=\sqrt{64+{{\left( y+3 \right)}^{2}}}$
Since the distance between them is $10$ units,
$\sqrt{64+{{\left( y+3 \right)}^{2}}}=10$
Squaring on both sides, we get,
$64+{{\left( y+3 \right)}^{2}}=100$
${{\left( y+3 \right)}^{2}}=36$
$y+3=\pm 6$
So, $y+3=6$
$y=3$
And, $y+3=-6$
$y=-9$
$\therefore $The possible values of $y$ are $y=3$ or $y=-9$.
9. If $Q\left( 0,1 \right)$ is equidistant from $P\left( 5,-3 \right)$ and $R\left( x,6 \right)$, find the values of $x$. Also find the distance of $QR$ and $PR$.
Ans:
Given that,
$Q\left( 0,1 \right)$
$P\left( 5,-3 \right)$
$R\left( x,6 \right)$
To find,
The values of $x$
The distance of $QR$ and $PR$
$Q$ is equidistant between $P$ and $R$.
SO $PQ=QR$
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
$\sqrt{{{\left( 5-0 \right)}^{2}}+{{\left( -3-1 \right)}^{2}}}=\sqrt{{{\left( 0-x \right)}^{2}}+{{\left( 1-6 \right)}^{2}}}$
$\sqrt{{{\left( 5 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{{{\left( -x \right)}^{2}}+{{\left( -5 \right)}^{2}}}$
$\sqrt{25+16}=\sqrt{{{x}^{2}}+25}$
Squaring on both sides, we get,
$41={{x}^{2}}+25$
${{x}^{2}}=16\pi $
x = ±4
Thus the point $R$ is $R\left( 4,6 \right)$ or $\left( -4,6 \right)$.
To find the distance $PR$ and $QR$
Case (1):
When the point is $R\left( 4,6 \right)$
Distance between the point $P\left( 5,-3 \right)$ and $R\left( 4,6 \right)$ is,
$PR=\sqrt{{{\left( 5-4 \right)}^{2}}+{{\left( -3-6 \right)}^{2}}}$
$=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( -9 \right)}^{2}}}$
$=\sqrt{1+81}$
$=\sqrt{82}$
Distance between the point $Q\left( 0,1 \right)$ and $R\left( 4,6 \right)$,
$QR=\sqrt{{{\left( 0-4 \right)}^{2}}+{{\left( 1-6 \right)}^{2}}}$
$=\sqrt{{{\left( -4 \right)}^{2}}+{{\left( -5 \right)}^{2}}}$
$=\sqrt{16+25}$
$=\sqrt{41}$
Case (2):
When the point is $R\left( -4,6 \right)$
Distance between the point $P\left( 5,-3 \right)$ and $R\left( 4,6 \right)$,
$PR=\sqrt{{{\left( 5-\left( -4 \right) \right)}^{2}}+{{\left( -3-6 \right)}^{2}}}$
$=\sqrt{{{\left( 9 \right)}^{2}}+{{\left( -9 \right)}^{2}}}$
$=\sqrt{81+81}$
$=\sqrt{162}$
$=9\sqrt{2}$
Distance between the point $Q\left( 0,1 \right)$ and $R\left( 4,6 \right)$,
$QR=\sqrt{{{\left( 0-\left( -4 \right) \right)}^{2}}+{{\left( 1-6 \right)}^{2}}}$
$=\sqrt{{{\left( 4 \right)}^{3}}+{{\left( -5 \right)}^{2}}}$
$=\sqrt{16+25}$
$=\sqrt{41}$
10. Find a relation between $x$ and $y$ such that the point $\left( x,y \right)$ is equidistant from the point $\left( 3,6 \right)$ and $\left( -3,4 \right)$.
Ans:
Given that,
$\left( x,y \right)$ is equidistant from $\left( 3,6 \right)$ and $\left( -3,4 \right)$
To find,
The value of $\left( x,y \right)$
Let $P\left( x,y \right)$ is equidistant from $A\left( 3,6 \right)$ and $B\left( -3,4 \right)$
Since they are equidistant,
$PA=PB$
$=66\text{ c}{{\text{m}}^{3}}\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}=\sqrt{\left( x-{{\left( -3 \right)}^{2}} \right)+{{\left( y-4 \right)}^{2}}}$
$\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}=\sqrt{{{\left( x+3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}}$
Squaring on both sides, we get,
${{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}={{\left( x+3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}$
${{x}^{2}}+9-6x+{{y}^{2}}+36-12y={{x}^{2}}+9+6x+{{y}^{2}}+16-8y$
$36-16=12x+4y$
$3x+y=5$
$3x+y-5=0$
$\therefore $The relation between $x$ and $y$ is given by $3x+y-5=0$
Exercise (7.2)
1.Find the coordinates of the point which divides the join of $\left( -1,7 \right)$ and $\left( 4,-3 \right)$ in the ratio $2:3$
Ans:
Given that,
The points $A\left( -1,7 \right)$ and $B\left( 4,-3 \right)$
Ratio $m:n=$ $2:3$
To find,
The coordinates
Let $P\left( x,y \right)$ be the required coordinate
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
$P\left( x,y \right)=\left[ \frac{2\left( 4 \right)+3\left( -1 \right)}{2+3},\frac{2\left( -3 \right)+3\left( 7 \right)}{2+3} \right]$
$=\left[ \frac{8-3}{5},\frac{-6+21}{5} \right]$
$=\left[ \frac{5}{5},\frac{15}{5} \right]$
$=\left( 1,3 \right)$
$\therefore $The coordinates of $P$ is $P\left( 1,3 \right)$.
2. Find the coordinates of the point of trisection of the line segment joining $\left( 4,-1 \right)$ and $\left( -2,-3 \right)$.
Ans:
Given that,
The line segment joining $\left( 4,-1 \right)$ and $\left( -2,-3 \right)$
To find,
The coordinates of the point
Let the line segment joining the points be $A\left( 4,-1 \right)$ and $B\left( -2,-3 \right)$
Let $P\left( {{x}_{1}},{{y}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}} \right)$ are the points of trisection of the line segment joining the points
$AP=PQ=QB$
From the diagram, the point $P$ divides $AB$ internally in the ratio of $1:2$
Hence $m:n=1:2$
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
$P\left( {{x}_{1}},{{y}_{1}} \right)=\left[ \frac{1\left( -2 \right)+1\left( 4 \right)}{1+2},\frac{1\left( -3 \right)+2\left( -1 \right)}{1+2} \right]$
$=\left[ \frac{-2+8}{3},\frac{-3-2}{3} \right]$
$=\left[ \frac{6}{3},\frac{-5}{3} \right]$
$=\left( 2,-\frac{5}{3} \right)$
$\therefore $The coordinates of $P$ is $P\left( 2,-\frac{5}{3} \right)$.
From the diagram, the point $Q$ divides $AB$ internally in the ratio of $2:1$
Hence $m:n=2:1$
By section formula,
$Q\left( {{x}_{2}},{{y}_{2}} \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
$Q\left( {{x}_{2}},{{y}_{2}} \right)=\left[ \frac{2\left( -2 \right)+1\left( 4 \right)}{2+1},\frac{2\left( -3 \right)+3\left( -1 \right)}{2+1} \right]$
$=\left[ \frac{-4+4}{3},\frac{-6-1}{3} \right]$
$=\left[ 0,-\frac{7}{3} \right]$
$\therefore $The coordinates of $Q$ is $Q\left( 0,-\frac{7}{3} \right)$.
3. To conduct Sports day activities, in your rectangular shaped school ground $ABCD$, lines have been drawn with chalk powder at a distance of $1\text{ m}$ each. $100$ flower pots have been placed at a distance of $1\text{ m}$ from each other along $AD$, as shown in the following figure. Niharika runs $\frac{1}{4}\text{ th}$ the distance $AD$ on the $2\text{nd}$ line and posts a green flag. Preet runs $\frac{1}{5}\text{ th}$the distance $AD$ on the eighth line and posts a red flag. What is the distance between both the flags?If Rashmi has to post a blue flag exactly halfway between the line segments joining the two flags, where should she post her flag?

Ans:
Given that,
Niharika posted her green flag at a distance of $P$which is $\frac{1}{4}\times 100=25\text{ m}$from the starting point of the second line. The coordinate of $P$ is $P\left( 2,25 \right)$
Preet posted red flag at $\frac{1}{5}$ of a distance $Q$ which is $\frac{1}{5}\times 100=20\text{ m}$from the starting point of the eighth line. The coordinate of $Q$ is $\left( 8,20 \right)$
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
The distance between the flags $P\left( 2,25 \right),Q\left( 8,20 \right)$ is given by,
$PQ=\sqrt{{{\left( 8-2 \right)}^{2}}+{{\left( 25-20 \right)}^{2}}}$
$=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 5 \right)}^{2}}}$
$=\sqrt{36+25}$
$=\sqrt{61}\text{ m}$
Rashmi should post her blue flag in the mid-point of the line joining points $P$ and $Q$. Let this point be $M\left( x,y \right)$.
By section formula,
$M\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
$M\left( x,y \right)=\left[ \frac{1\left( 2 \right)+1\left( 8 \right)}{1+1},\frac{1\left( 25 \right)+1\left( 20 \right)}{1+1} \right]$
$=\left[ \frac{2+8}{2},\frac{25+20}{2} \right]$
$=\left[ \frac{10}{2},\frac{45}{2} \right]$
$=\left( 5,22.5 \right)$
$\therefore $Rashmi should place her blue flag at $22.5\text{ m}$ in the fifth line.
4. Find the ratio in which the line segment joining the points $\left( -3,10 \right)$ and $\left( 6,-8 \right)$ is divided by $\left( -1,6 \right)$
Ans:
Given that,
The line segment $\left( -3,10 \right)$ and $\left( 6,-8 \right)$
The point $\left( -1,6 \right)$ divides the line segment
To find,
The ratio of dividing line segment
Let the line segment be $A\left( -3,10 \right)$ and $B\left( 6,-8 \right)$ divided by point $P\left( -1,6 \right)$in the ratio of $k:1$
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
Equating the $x$term,
$-1=\frac{6k-3}{k+1}$
$-k-1=6k-3$
$7k=2$
$k=\frac{2}{7}$
$\therefore $The point $P$ divides the line segment $AB$ in the ratio of $2:7$
5. Find the ratio in which the line segment joining $A\left( 1,-5 \right)$ and $B\left( -4,5 \right)$ is divided by the $x$ axis. Also find the coordinates of the point of division.
Ans:
Given that,
The line segment joining the points $A\left( 1,-5 \right)$ and $B\left( -4,5 \right)$
To find,
The ratio
The coordinates of the point of division
Let the ratio be $k:1$
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
$P\left( x,y \right)=\left[ \frac{k\left( -4 \right)+1\left( 1 \right)}{k+1},\frac{k\left( 5 \right)+1\left( -5 \right)}{k+1} \right]$
$=\left[ \frac{-4k+1}{k+1},\frac{5k-5}{k+1} \right]$
We know that $y$ coordinate on $x$ axis is zero.
$\frac{5k-5}{k+1}=0$
$5k-5=0$
$5k=5$
$k=1$
Therefore $x$ axis divides it in the ratio of $1:1$
Division point, $P=\left( \frac{-4\left( 1 \right)+1}{1+1},\frac{5\left( 1 \right)-5}{1+1} \right)$
$=\left( \frac{-4+1}{2},\frac{5-5}{2} \right)$
$=\left( -\frac{3}{2},0 \right)$
$\therefore $The ratio at which the line segment is divided is $1:1$ and the point of division is $\left( -\frac{3}{2},0 \right)$.
6. If $\left( 1,2 \right),\left( 4,y \right),\left( x,6 \right)$ and $\left( 3,5 \right)$ are the vertices of the parallelogram taken in order, find $x$ and $y$.
Ans:
Given that,
The vertices of the parallelogram are $A\left( 1,2 \right),B\left( 4,y \right),C\left( x,6 \right),D\left( 3,5 \right)$
To find,
The value of $x$ and $y$
The diagonals of the parallelogram bisect each other at $O$.
Intersection point $O$ of diagonal $AC$ and $BD$divides these diagonals. So $O$ is the midpoint of $AC$ and $BD$.
If $O$ is the midpoint of $AC$,
$O=\left( \frac{1+x}{2},\frac{2+6}{2} \right)$
$=\left( \frac{1+x}{2},\frac{8}{2} \right)$
$=\left( \frac{1+x}{2},4 \right)$
If $O$ is the midpoint of $BD$,
$O=\left( \frac{4+3}{2},\frac{5+y}{2} \right)$
$=\left( \frac{7}{2},\frac{5+y}{2} \right)$
Equating the points of $O$,
$\frac{x+1}{2}=\frac{7}{2}$ and
$4=\frac{5+y}{2}$
Finding $x$ term,
$\frac{x+1}{2}=\frac{7}{2}$
$x+1=7$
$x=6$
Finding $y$ term,
$4=\frac{5+y}{2}$
$5+y=8$
$y=3$
The value of $x$ and $y$ are $x=6$ and $y=3$
7. Find the coordinates of point $A$, where $AB$ is the diameter of circle whose center is $\left( 2,-3 \right)$ and $B$ is $\left( 1,4 \right)$
Ans:
Given that,
Center is $C\left( 2,-3 \right)$
The coordinate of $B$ is $B\left( 1,4 \right)$
To find,
The coordinate of $A$
Let the coordinate of $A$ be $A\left( x,y \right)$
Midpoint of $AB$ is $C\left( 2,-3 \right)$and so,
$\left( 2,-3 \right)=\left( \frac{x+1}{2},\frac{y+4}{2} \right)$
Equating $x$ term,
$\frac{x+1}{2}=2$
$x+1=4$
$x=3$
Equating $y$ term,
$\frac{y+4}{2}=-3$
$y+4=-6$
$y=-10$
$\therefore $The coordinate of $A$ is $A\left( 3,-10 \right)$
8. If $A$ and $B$ are $\left( -2,-2 \right)$ and $\left( 2,-4 \right)$ respectively, find the coordinates of $P$ such that $AP=\frac{3}{7}AB$ and $P$ lies on the line segment $AB$.
Ans:
Given that,
The coordinates are $A\left( -2,-2 \right)$ and $B\left( 2,-4 \right)$
$AP=\frac{3}{7}AB$
To find,
The coordinate of $P$
$AP=\frac{3}{7}AB$
$\frac{AB}{AP}=\frac{7}{3}$
From the figure, $AB=AP+PB$
$\frac{AP+PB}{AP}=\frac{3+4}{3}$
$1+\frac{PB}{AP}=1+\frac{4}{3}$
$\frac{PB}{AP}=\frac{4}{3}$
$\therefore AP:PB=3:4$
Thus, the point $P\left( x,y \right)$ divides the line segment $AB$ in the ratio of $3:4$
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
$P\left( x,y \right)=\left[ \frac{3\left( 2 \right)+4\left( -2 \right)}{3+4},\frac{3\left( -4 \right)+4\left( -2 \right)}{3+4} \right]$
$=\left[ \frac{6-8}{7},\frac{-12-8}{7} \right]$
$=\left[ -\frac{2}{7},-\frac{20}{7} \right]$
$\therefore $The coordinates of $P$ is $P\left( -\frac{2}{7},-\frac{20}{7} \right)$.
7. Find the coordinates of the points which divide the line segment joining $A\left( -2,2 \right)$ and $B\left( 2,8 \right)$ into four equal parts.
Ans;
Given that,
The line segment $A\left( -2,2 \right)$ and $B\left( 2,8 \right)$
To find,
The coordinate that divides the line segment into four equal parts
Form the figure, ${{P}_{1}},{{P}_{2}},{{P}_{3}}$ be the points that divide the line segment $AB$ into four equal parts.
Point ${{P}_{1}}$ divides the line segment $AB$ in the ratio of $1:3$, so,
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
${{P}_{1}}\left( x,y \right)=\left[ \frac{1\left( 2 \right)+3\left( -2 \right)}{1+3},\frac{1\left( 8 \right)+3\left( 2 \right)}{1+3} \right]$
$=\left[ \frac{-4}{4},\frac{14}{4} \right]$
$=\left( -1,\frac{7}{2} \right)$
Point ${{P}_{2}}$ divides the line segment $AB$ in the ratio of $1:1$, so,
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
${{P}_{2}}\left( x,y \right)=\left[ \frac{1\left( 2 \right)+1\left( -2 \right)}{1+1},\frac{1\left( 8 \right)+1\left( 2 \right)}{1+1} \right]$
$=\left[ \frac{2+\left( -2 \right)}{2},\frac{2+8}{2} \right]$
$=\left( 0,5 \right)$
Point ${{P}_{3}}$ divides the line segment $AB$ in the ratio of $3:1$, so,
By section formula,
$P\left( x,y \right)=\left[ \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right]$
${{P}_{3}}\left( x,y \right)=\left[ \frac{3\left( 2 \right)+1\left( -2 \right)}{3+1},\frac{3\left( 8 \right)+1\left( 2 \right)}{3+1} \right]$
$=\left[ \frac{6-2}{4},\frac{24+2}{4} \right]$
$=\left( 1,\frac{13}{2} \right)$
The coordinates that divide the line segment into four equal parts are ${{P}_{1}}\left( -1,\frac{7}{2} \right),{{P}_{2}}\left( 0,5 \right)$ and ${{P}_{3}}\left( 1,\frac{13}{2} \right)$
10. Find the area of the rhombus if its vertices are $\left( 3,0 \right),\left( 4,5 \right),\left( -1,4 \right)$ and $\left( -2,-1 \right)$ taken in order. (Hint: Area of a rhombus = $\frac{1}{2}$(Product of its diagonals))
Ans:
Given that,
The vertices of the rhombus are $A\left( 3,0 \right),B\left( 4,5 \right),C\left( -1,4 \right)$ and $D\left( -2,-1 \right)$
To find,
The area of the rhombus
The distance between any two points is given by the Distance formula,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Distance between the diagonal $AC$ is given by,
$AC=\sqrt{{{\left( 3-\left( -1 \right) \right)}^{2}}+{{\left( 0-4 \right)}^{2}}}$
$=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( -4 \right)}^{2}}}$
$=\sqrt{16+16}$
$=\sqrt{32}$
$=4\sqrt{2}$
Distance between the diagonal $BD$ si given by,
$BD=\sqrt{{{\left( 4-\left( -2 \right) \right)}^{2}}+{{\left( 5-\left( -1 \right) \right)}^{2}}}$
$=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 6 \right)}^{2}}}$
$=\sqrt{36+36}$
$=\sqrt{72}$
$=6\sqrt{2}$
Area of the rhombus = $\frac{1}{2}\times $(Products of lengths of diagonals
$=\frac{1}{2}\times AC\times BD$
$=\frac{1}{2}\times 4\sqrt{2}\times 6\sqrt{2}$
$=24$ square units
What is Coordinate Geometry
Coordinate Geometry is the branch of mathematics that helps us to exactly locate a given point with the help of an ordered pair of numbers. Coordinate geometry is the combination of geometry and algebra to solve the problems. It helps you find the distance between two points whose coordinates are given. You can also find the coordinates of the point which divides the line segment joining two given points in the given ratio.
Coordinate geometry is also said to be the study of graphs. Graphs are visual representations of our data. It can be in different forms like bar graphs, histograms, line graphs, etc.
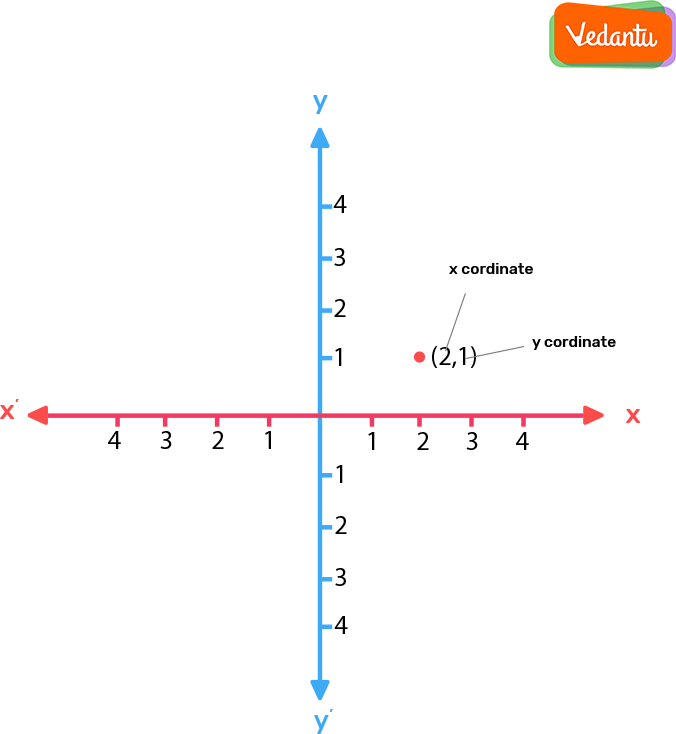
Terms Related to Coordinate Geometry
While studying coordinate geometry the students must be aware of some important terms related to coordinate geometry they are well explained in this chapter.

From this figure, let us understand some important terms used in the coordinate formula of geometry.
Axes of Coordinates
In the above figure OX and OY are called X-axis and Y-axis respectively and both together are known as axes of coordinates.
Origin
The point of intersection of the axes is called the origin; it is O.
Abscissa
The distance of any point on the plane from the Y-axis is called the abscissa.
Ordinate
The distance of any point on the plane from the X-axis is said to be ordinate.
Coordinate of the Origin
It has zero distance from both the axes. Therefore the coordinates of the origin are (0, 0).
Quadrant
The axes divide the plane into four parts. These four parts are said to be quadrants.
A quadrant is ¼ th part of a plane divided by coordinate axes. The plane is called the coordinate plane or the XY-plane and the axes are called the coordinate axes.

In the first quadrant, both the coordinates are positive.
In the second quadrant, the y-coordinate is positive and x-coordinate is negative.
In the third quadrant, both the coordinates are negative.
In the fourth quadrant, the y-coordinate is negative and the x-coordinate is positive.
Distance Formula
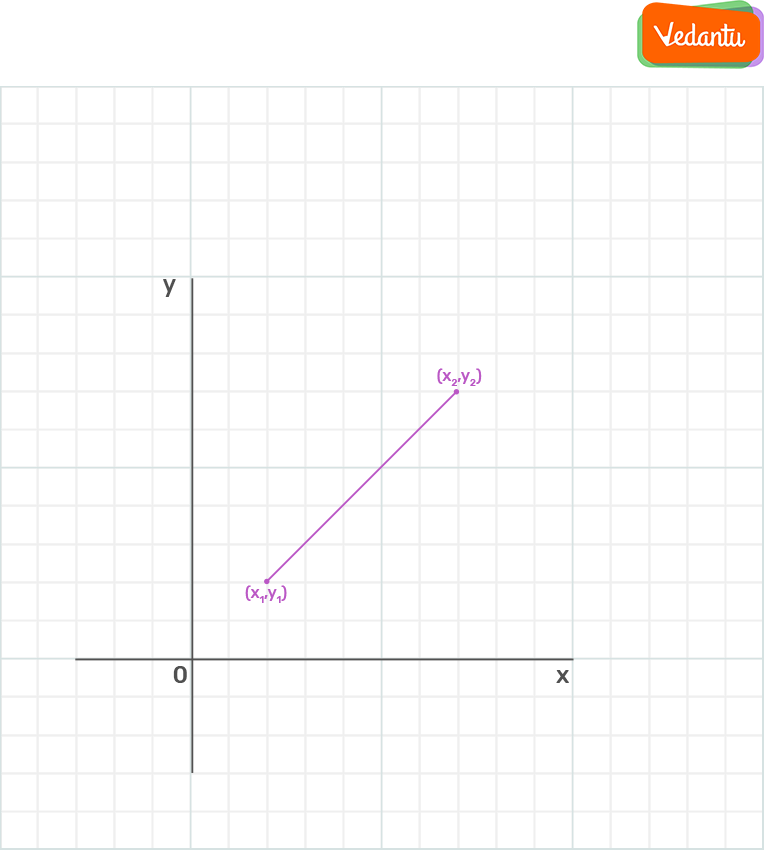
In chapter 7 Maths Class 10 we learn about distance formulas for finding distance between two points. Finding the distance between the two points by using formula when the two coordinates of the points are given.
Distance between two points O(x1,y1) and B(x2, y2) =OB = \[\sqrt{[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}]}\]
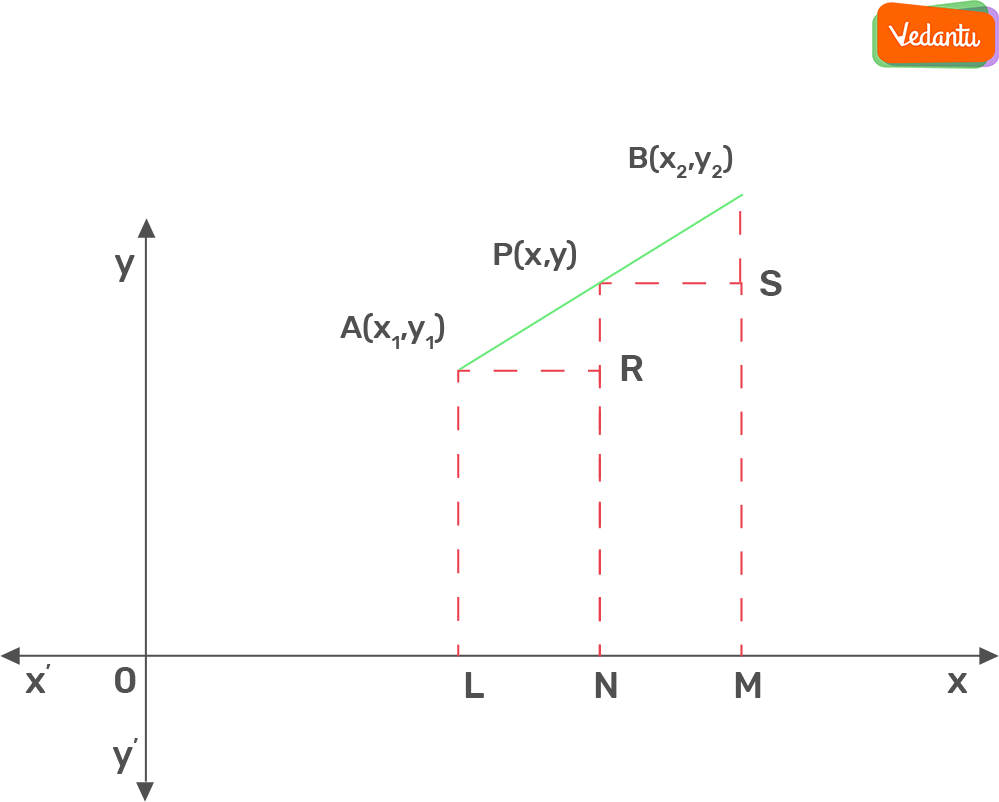
Section Formula
Section formula helps us in finding the coordinates of the point dividing the line in the ratio m:n.
If P is the point dividing the line AB in the ratio m:n where coordinates of A(x1, y1) and B(x2, y2).
The coordinates of P will be $\left( \frac{mx_2 + nx_1}{m + n}, \frac{my_2 + ny_1}{m + n} \right)$
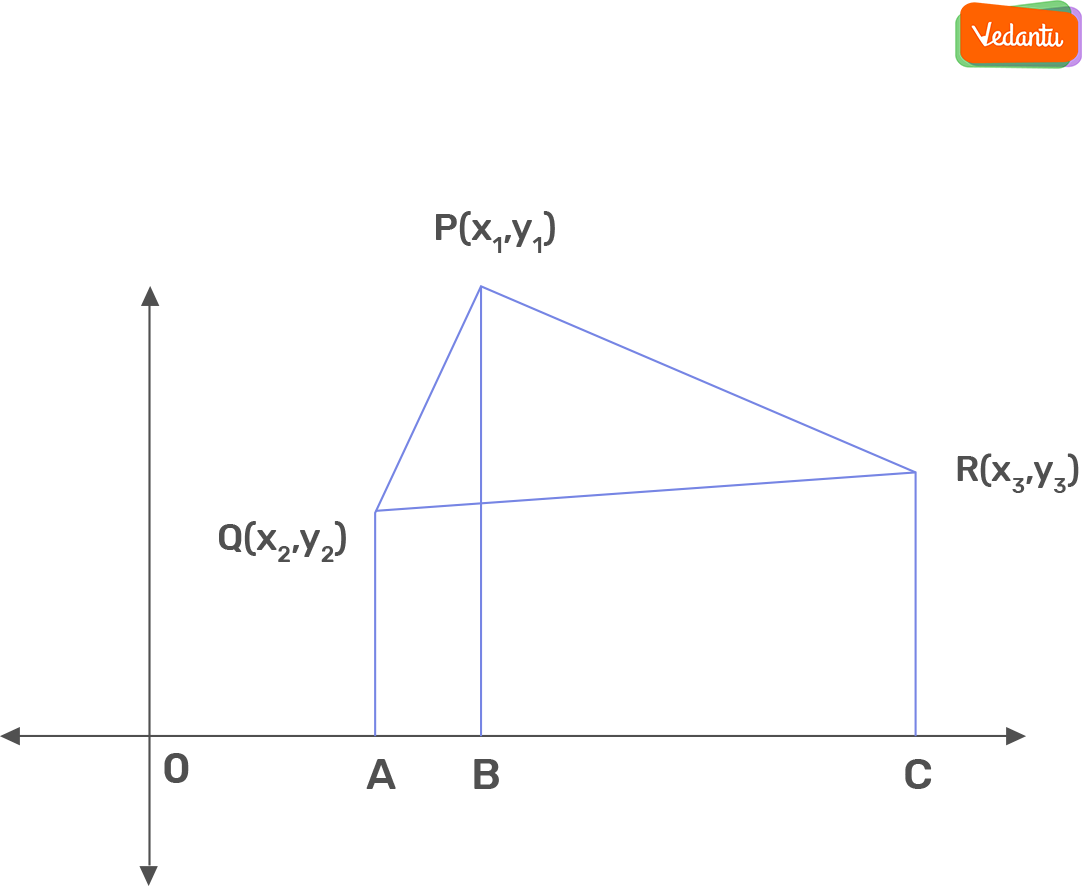
Area of Triangle
It will let us find the area of any triangle in terms of coordinates of its vertices. This formula will also be used in finding the area of quadrilaterals.
Area of a Triangle = ½ |x1(y2−y3)+x2(y3–y1)+x3(y1–y2)|
All the basic formulas of coordinate geometry will help you to solve your geometry and algebra problems.
Chapter 7 maths Class 10 provides you the list of all formulas of coordinate geometry to solve all the related problems.
Table of All Formulas of Coordinate Geometry
General Form of a Line | Ax + By + C = 0 Where A , B, C are real numbers and x and y are variables |
Slope Intercept Form of a Line | $y = m \times x + c$ Where x and y are variables, c is constant and m is the slope |
Point-Slope Form | $Y-y1= m\times(x - x1)$ x1 ,y1,x2,y2 are the X Y coordinates and m is the slope |
The slope of a Line Using Coordinates | $m = \dfrac{Δy}{Δx} = \dfrac{(y2 − y1)}{(x2 − x1)}$ |
The slope of a Line Using General Equation | $m = −(\dfrac{A}{B})$ |
Intercept-Intercept Form | $\dfrac{x}{a} +\dfrac{y}{b} = 1$ |
Distance between two points O(x1,y1) and B(x2, y2) | OB= \[\sqrt{[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}]}\] |
For Parallel Lines, | m1 = m2 |
For Perpendicular Lines, | $m1\times m2 = -1$ |
Midpoint Formula/Section Formula | M (x, y) = [½(x1 + x2), ½(y1 + y2)] |
Angle between Two Lines | $θ = tan{-1} \left[\dfrac{(m_1 - m_2)}{ 1 + m_1m_2}\right]$ |
Area of a Triangle | ½ |x1(y2−y3)+x2(y3–y1)+x3(y1–y2)| |
Perpendicular Distance from a Point to a Line | $d = [\dfrac{|ax1 + by1 + c|}{ √(a2 + b2)}]$ |
Class 10 Maths Chapter 7: Exercises Breakdown
Chapter 7 Coordinate Geometry Exercises in PDF Format | |
Exercise 7.1 | 10 Questions & Solutions |
Exercise 7.2 | 10 Questions & Solutions |
Conclusion
NCERT Solutions for Class 10 Chapter 7 Coordinate Geometry offers a thorough grasp of this crucial subject. students can develop a strong foundation in coordinate geometry by concentrating on essential ideas such as recognising slopes, finding distances, and charting points. It's important to pay attention to the step-by-step solutions provided in the NCERT Solutions, as they help clarify concepts and reinforce problem-solving techniques. Coordinate geometry is important to comprehend because it provides the foundation for understanding more advanced mathematical ideas and has real-world applications in computer graphics, engineering, and architecture. In previous year question papers, around 5-6 questions have been typically asked from this chapter.
Other Study Material for CBSE Class 10 Maths Chapter 7
S.No. | Important links for Chapter 7 Coordinate Geometry |
1. | |
2. | |
3. | |
4. | |
5. | |
6. |
Chapter-Specific NCERT Solutions for Class 10 Maths
Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
S.No. | NCERT Solutions Class 10 Chapter-wise Maths PDF |
1 | |
2 | |
3 | Chapter 3 - Pair Of Linear Equations In Two Variables Solutions |
4 | |
5 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 |
Study Resources for Class 10 Maths
For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.
FAQs on Class 10 Maths Chapter 7 Coordinate Geometry NCERT Solution
1. What are the key concepts covered in NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry?
NCERT Solutions for Class 10 Maths Chapter 7 covers fundamental concepts such as plotting points on the Cartesian plane, understanding the coordinate axes, distance formula, section formula, area of triangles using coordinates, and types of lines (parallel, perpendicular). Mastery of these concepts is essential as per the latest CBSE 2025–26 syllabus.
2. How do you use the distance formula to find the distance between two points in coordinate geometry?
The distance between two points (x1, y1) and (x2, y2) is calculated using the formula:
- d = √[(x2−x1)² + (y2−y1)²]
3. What is the section formula, and how is it applied in NCERT Solutions for Class 10 Maths Chapter 7?
The section formula finds the coordinates of a point dividing a line segment between (x1, y1) and (x2, y2) in the ratio m:n:
- P(x, y) = [(mx2 + nx1)/(m+n), (my2 + ny1)/(m+n)]
4. How do you calculate the area of a triangle using coordinates in Class 10 Coordinate Geometry?
To find the area of a triangle with vertices at (x1, y1), (x2, y2), and (x3, y3):
- Area = ½ |x1(y2−y3) + x2(y3−y1) + x3(y1−y2)|
5. How is coordinate geometry used to verify if three points are collinear?
To check if points A, B, and C are collinear in coordinate geometry (Class 10 Maths Chapter 7):
- Calculate the area of triangle ABC using the coordinate area formula.
- If the area is zero, the points are collinear.
6. What is a Cartesian plane, and why are quadrants important in coordinate geometry?
A Cartesian plane (or coordinate plane) is formed by two perpendicular axes: the x-axis (horizontal) and y-axis (vertical), intersecting at the origin (0, 0). These axes divide the plane into four quadrants, which help in identifying the signs of the coordinates and correctly plotting points in NCERT Solutions for Class 10 Maths Chapter 7.
7. What are some common mistakes students make in applying the distance and section formulas?
Common errors include:
- Incorrect substitution of coordinates (mixing up x1 and x2)
- Sign errors when dealing with negative values
- Not simplifying ratios correctly in the section formula
- Forgetting to use absolute value for area calculations
8. How can coordinate geometry concepts be applied in real life, as covered by CBSE Class 10?
Coordinate geometry has practical uses such as:
- Finding locations using GPS (digital mapping)
- Designing layouts in engineering and architecture
- Computer graphics and animation
- Navigation and movement tracking
9. What is the difference between the midpoint formula and the section formula in coordinate geometry?
The midpoint formula finds the centre point of a line segment [(x1 + x2)/2, (y1 + y2)/2], a special case of the section formula where the ratio is 1:1. The section formula handles any given ratio, making it broader for NCERT problems in Chapter 7.
10. Why is understanding slopes important in coordinate geometry for Class 10 math?
The slope measures how steep a line is and helps in:
- Identifying parallel and perpendicular lines
- Writing equations of straight lines
- Solving higher-order questions involving angles
11. How do the concepts in Class 10 Maths Chapter 7 help with later studies in mathematics?
Concepts from Coordinate Geometry are building blocks for advanced topics such as calculus, vectors, 3D geometry, and analytic geometry, making this chapter critical for students aiming for higher studies in science and engineering.
12. What are the criteria for a quadrilateral to be a square or parallelogram in coordinate geometry?
For a square:
- All four sides are equal (using distance formula)
- Both diagonals are equal
- Opposite sides are equal
- Diagonals bisect each other (use midpoint formula)
13. What is the best step-by-step approach to solving NCERT Solutions for Class 10 Maths Chapter 7 exercises?
- Read the question carefully and identify what formula/concept is required
- Write all given data and coordinates clearly
- Apply the correct formula: distance, section, or area
- Show each calculation step as per CBSE marking scheme
- Simplify your answer and include correct units where relevant
14. Where can I access NCERT Solutions for Class 10 Maths Chapter 7 according to the 2025–26 CBSE syllabus?
NCERT Solutions for Class 10 Maths Chapter 7 can be found on Vedantu's official website, updated and aligned with the latest CBSE 2025–26 syllabus. Solutions cover all exercises with stepwise explanations matching current board requirements.
15. What should I revise before exams for maximum scoring in Coordinate Geometry, Chapter 7?
Revise all formulas (distance, section, area, midpoint, slope), ensure you can plot points, understand quadrants, and practice previous year board questions. Use solved NCERT solutions to check your method and accuracy.














 Watch Video
Watch Video

















