NCERT Solutions For Class 11 Chapter 2 - Structure of Atom

1.

(i). Calculate the Number of Electrons Which Will Together Weigh One Gram.

Ans: Mass of one electron = \[9.10939\times {{10}^{-31}}kg\]

Number of electrons that weigh \[9.10939\times {{10}^{-31}}kg\]= 1

Number of electrons that will weigh 1 g = \[1\times {{10}^{-3}}kg\]

\[\frac{1}{9.10939\times {{10}^{-31}}kg}(1\times {{10}^{-3}}kg)=0.1098\times {{10}^{-3+31}}\] 

\[=1.098\times {{10}^{27}}\]

(ii).Calculate the Mass and Charge of One Mole of Electrons.

Ans: Mass of one electron = \[9.10939\times {{10}^{-31}}kg\]

Mass of one mole of electron = \[(6.022\times {{10}^{23}})\times (9.10939\times {{10}^{-31}}kg)\] = \[5.48\times {{10}^{-7}}kg\] 

Charge on one electron = \[1.6022\times {{10}^{-19}}coulomb\] 

Charge on one mole of electron = \[(1.6022\times {{10}^{-19}})(6.022\times {{10}^{23}})\] = \[9.65\times {{10}^{4}}C\]

2.

(i).Calculate the Total Number of Electrons Present in One Mole of Methane.

Ans: Number of electrons present in 1 molecule of methane (\[C{{H}_{4}}\])= \[\{1(6)+4(1)\}=10\] 

Number of electrons present in 1 mole i.e., \[6.023\times {{10}^{23}}\] molecules of methane = \[6.023\times {{10}^{23}}\times 10=6.023\times {{10}^{24}}\] 

(ii). a) Find the Total Number of Neutrons in 7mg of ${}^{14}C$ . (Assume the Mass of a Neutron = $1.675\times {{10}^{-27}}kg$ )

Ans: Number of atoms of \[{}^{14}C\]in 1 mole = \[6.023\times {{10}^{23}}\] 

Since 1 atom of \[{}^{14}C\] contains (14-6) i.e., 8 neutrons, the number of neutrons in 14g of \[{}^{14}C\] is \[(6.023\times {{10}^{23}})\times 8\] 

Number of neutrons in 7 mg 

\[=\frac{6.022\times {{10}^{23}}\times 8\times 7}{1400mg}\] 

\[=2.4092\times {{10}^{21}}\] 

(b) Find the Total Mass of Neutrons in 7mg of ${}^{14}C$ . (Assume the Mass of a Neutron = $1.675\times {{10}^{-27}}kg$ )

Ans: Mass of one neutron = \[1.67493\times {{10}^{-27}}kg\] Mass of total neutrons in 7g of \[{}^{14}C\]

\[=(2.4092\times {{10}^{21}})(1.67493\times {{10}^{-27}}kg)\] 

\[=4.0352\times {{10}^{-6}}kg\] 

(iii). (a) Find the Total Number of Protons in 34mg of $N{{H}_{3}}$ at STP. 

Ans: 1 mole of \[N{{H}_{3}}\] = {1(14) +3(1)} g of \[N{{H}_{3}}\] = 17g of \[N{{H}_{3}}\] 

\[=6.023\times {{10}^{23}}\] Molecules of \[N{{H}_{3}}\] 

Total number of protons present in 1 molecule of \[N{{H}_{3}}\]

 = [1(7) +1(3)] =10

Number of protons in \[6.023\times {{10}^{23}}\] molecules of \[N{{H}_{3}}\] 

\[=(6.023\times {{10}^{23}})(10)=6.023\times {{10}^{24}}\] 

 17g of \[N{{H}_{3}}\] contains \[(6.023\times {{10}^{24}})\] protons.

Number of protons in 34mg of \[N{{H}_{3}}\] 

\[=\frac{6.022\times {{10}^{24}}\times 34mg}{1700mg}\] 

\[=1.2046\times {{10}^{22}}\] 

(b) Find the total mass of protons in 34mg of $N{{H}_{3}}$ at STP. Will the answer change if the temperature and pressure changed?

Ans: Mass of one proton = \[1.67493\times {{10}^{-27}}kg\] 

Total mass of protons in 34mg of \[N{{H}_{3}}\] 

\[=(1.67493\times {{10}^{-27}}kg)(1.2046\times {{10}^{22}})\] 

\[=2.0176\times {{10}^{-5}}kg\] 

The number of protons, electrons, and neutrons in an atom is independent of temperature and pressure conditions. Hence, the obtained values will remain unchanged if the temperature and pressure is changed.

3. How Many Neutrons and Protons are There in the Following Nuclei? \[_{6}^{13}C,_{8}^{16}O,_{12}^{24}Mg,_{26}^{56}Fe,_{38}^{88}Sr\] 

Ans: $_{6}^{13}C$ :

Atomic mass =13

Atomic number = Number of Protons = 6

Number of neutrons = (Atomic Mass)-(Atomic Number)=13-6=7

$_{8}^{16}O$ :

Atomic mass =16

Atomic number = Number of Protons = 8

Number of neutrons = (Atomic Mass)-(Atomic Number) =16-8=8

$_{12}^{24}Mg$ :

Atomic mass =24

Atomic number = Number of Protons = 12

Number of neutrons = (Atomic Mass)-(Atomic Number)=24-12 =12

$_{26}^{56}Fe$ :

Atomic mass = 56

Atomic number = Number of Protons = 26

Number of neutrons = (Atomic Mass)-(Atomic Number) = 56-26=30

$_{38}^{88}Sr$ :

Atomic mass = 88 

Atomic number = Number of Protons = 38

Number of neutrons = (Atomic Mass)-(Atomic Number)= 88-38=50

4. Write the Complete Symbol for the Atom with the Given Atomic Number (Z) and Atomic mass (A)

a. Z = 17, A = 35

Ans: $_{17}^{35}Cl$

b. Z = 92, A = 233

Ans: $_{92}^{233}U$

c. Z = 4, A = 9

Ans: $_{4}^{9}Be$ 

5. Yellow light emitted from a sodium lamp has a wavelength ($\lambda $ ) of 580 nm. Calculate the frequency ($\upsilon $) and wave number ( $\overset{-}{\mathop{\upsilon }}\,$ ) of the yellow light. 

Ans:

From the expression,

\[\lambda =\frac{c}{\upsilon }\] 

We get,

$\upsilon =\frac{c}{\lambda }$ ----- (i)

Where, 

$\upsilon $ = frequency of yellow light

c = velocity of light in vacuum = $3\times {{10}^{8}}m/s$ 

$\lambda $ = wavelength of yellow light = 580nm = $580\times {{10}^{-9}}m$

Substituting the values in the expression (i)

\[\upsilon =\frac{3\times {{10}^{8}}}{580\times {{10}^{-9}}}=5.17\times {{10}^{14}}{{S}^{-1}}\] 

Thus, frequency of yellow light emitted from sodium lamp 

= $5.17\times {{10}^{14}}{{S}^{-1}}$ 

Wave number of yellow light, \[\overset{-}{\mathop{\upsilon }}\,=\frac{1}{\lambda }=\frac{1}{580\times {{10}^{-9}}m}=1.72\times {{10}^{6}}{{m}^{-1}}\]   

6.

(i). Find energy of each of the photons which correspond to light of frequency $3\times {{10}^{15}}Hz$ 

Ans: Energy (E) of a photon is given by the expression,

\[E=h\upsilon \] 

Where, h = Planck’s constant = $6.626\times {{10}^{-34}}Js$ 

$\upsilon $ = frequency of light = $3\times {{10}^{15}}Hz$ 

Substituting the values in the given expression of Energy, $E=(6.626\times {{10}^{-34}})(3\times {{10}^{15}})=1.988\times {{10}^{-18}}J$

(ii). Find energy of each of the photons which have wavelength of $0.50{{A}^{o}}$ 

Ans: Energy (E) of a photon having wavelength ($\lambda $) is given by the expression,

\[E=\frac{hc}{\lambda }\] 

Where, h = Planck’s constant = $6.626\times {{10}^{-34}}Js$

c = velocity of light in vacuum = $3\times {{10}^{8}}m/s$

$\lambda $ = wavelength of yellow light = $0.50{{A}^{o}}$ = $0.5\times {{10}^{-10}}m$

 \[E=\frac{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}{0.5\times {{10}^{-10}}}J\] 

\[E=3.98\times {{10}^{-15}}J\] 

7. Calculate the wavelength, frequency and wave number of a light wave whose period is $2.0\times {{10}^{-10}}s$ 

Ans: Frequency ($\upsilon $) of light = $\frac{1}{period}=\frac{1}{2\times {{10}^{-10}}s}=5\times {{10}^{9}}{{s}^{-1}}$ 

Wavelength of light, \[\lambda =\frac{c}{\upsilon }\] 

c = velocity of light in vacuum = $3\times {{10}^{8}}m/s$

Substitution the value in the given expression $\lambda $ ,

 \[\lambda =\frac{3\times {{10}^{8}}}{5\times {{10}^{9}}}=6.0\times {{10}^{-2}}m\] 

Wave number of light, $\overset{-}{\mathop{\upsilon }}\,=\frac{1}{\lambda }=\frac{1}{6.0\times {{10}^{-2}}}=16.66m$ 

8. What is the number of photons of light with a wavelength of 4000 pm that provide 1 J of energy?

Ans: Energy (E) of a photon is given by the expression,

\[E=h\upsilon \] 

Energy of ‘n’ photons, 

\[{{E}_{n}}=nh\upsilon \] 

\[\Rightarrow n=\frac{{{E}_{n}}\lambda }{hc}\] 

Where, $\lambda $ = wavelength of yellow light = $4000pm=4000\times {{10}^{-12}}m$ 

c = velocity of light in vacuum = $3\times {{10}^{8}}m/s$

h = Planck’s constant = $6.626\times {{10}^{-34}}Js$

Substituting the values in the given expression ‘n’,

\[n=\frac{(1)\times (4000\times {{10}^{-12}})}{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}=2.012\times {{10}^{16}}\] 

Hence, the number of photons with a wavelength of 4000 pm and energy of 1 J are $2.012\times {{10}^{16}}$ 

9. A photon of wavelength $4\times {{10}^{7}}m$ strikes on metal surface, the work function of the metal being 2.13eV. 

(i). Calculate the energy of photon (eV)

Ans: Energy of photon, $E=h\upsilon =\frac{hc}{\lambda }$ 

Where, c = velocity of light in vacuum = $3\times {{10}^{8}}m/s$

h = Planck’s constant = $6.626\times {{10}^{-34}}Js$

$\lambda $ = wavelength of yellow light = $4\times {{10}^{-7}}m$

Substituting the values in the given expression of E,

\[E=\frac{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}{4\times {{10}^{-7}}}=4.9695\times {{10}^{-19}}J\] 

Hence, the energy of photon is $4.9695\times {{10}^{-19}}J$

(ii). Calculate the kinetic energy of the emission.

Ans: the kinetic energy of emission is given by,

\[{{E}_{k}}=h\upsilon -h{{\upsilon }_{0}}=(E-W)eV\] 

\[=[\frac{4.9696\times {{10}^{-19}}}{1.6020\times {{10}^{-19}}}]-2.13eV=0.9720eV\] 

Hence, the kinetic energy of emission is 0.97eV

(iv). Calculate the velocity of the photoelectron ($1eV=1.6020\times {{10}^{-19}}J$ )

Ans: The velocity of a photoelectron (ν) can be calculated by the expression,

\[\frac{1}{2}m{{v}^{2}}=h\upsilon -h{{\upsilon }_{0}}\] 

\[\Rightarrow v=\sqrt{\frac{2(h\upsilon -h{{\upsilon }_{0}})}{m}}\] 

Where, $h\upsilon -h{{\upsilon }_{0}}$ is the kinetic energy of emission in Joules and ‘m’ is the mass of the photoelectron. Substituting the values in the given expression of v:

\[v=\sqrt{\frac{2(0.9720\times 1.6020\times {{10}^{-19}})}{9.10939\times {{10}^{-31}}kg}J}\] 

 \[\Rightarrow v=\sqrt{0.3418\times {{10}^{12}}{{m}^{2}}{{s}^{-2}}}=5.84\times {{10}^{5}}m{{s}^{-1}}\] 

Hence, the velocity of the photoelectron is $5.84\times {{10}^{5}}m{{s}^{-1}}$ 

10. Electromagnetic radiation of wavelength 242 nm is just sufficient to ionize the sodium atom. Calculate the ionization energy of sodium in $kJmo{{l}^{-1}}$ 

Ans: Energy of sodium, $E=\frac{{{N}_{A}}hc}{\lambda }$ 

\[E=\frac{(6.023\times {{10}^{23}}mo{{l}^{-1}})(6.626\times {{10}^{-34}}Js)(3\times {{10}^{8}}m{{s}^{-1}})}{242\times {{10}^{-9}}m}=4.947\times {{10}^{5}}Jmo{{l}^{-1}}\] 

Hence, the ionization energy of sodium is $494kJmo{{l}^{-1}}$ 

11.  A 25 watt bulb emits monochromatic yellow light of wavelength of $0.57\mu m$ . Calculate the rate of emission of quanta per second.

Ans: power of Bulb, P = 25 Watt = $25J{{s}^{-1}}$ 

Energy of one photon, $E=h\upsilon =\frac{hc}{\lambda }$

Substituting the values in the given expression of E,

 \[E=\frac{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}{0.57\times {{10}^{-6}}}=34.87\times {{10}^{-20}}J\] 

Rate of emission of quanta per second,

\[=\frac{25}{34.87\times {{10}^{-20}}}=7.169\times {{10}^{19}}{{s}^{-1}}\] 

12. Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength$6800{{A}^{0}}$. Calculate threshold frequency (${{\upsilon }_{0}}$) and the work function (${{w}_{0}}$) of the metal.

Ans: Threshold wavelength of radian (${{\lambda }_{0}}$) = $6800{{A}^{0}}=6800\times {{10}^{10}}m$ 

Threshold frequency of metal (${{\upsilon }_{0}}$) = $\frac{c}{{{\lambda }_{0}}}=\frac{3\times {{10}^{8}}m{{s}^{-1}}}{6.8\times {{10}^{-7}}m}=4.41\times {{10}^{14}}{{s}^{-1}}$ 

Thus, threshold frequency of the metal is $4.41\times {{10}^{14}}{{s}^{-1}}$ 

Hence, the work function of the metal is,

\[{{w}_{0}}=h{{v}_{0}}=(6.626\times {{10}^{-34}}Js)(4.41\times {{10}^{14}}{{s}^{-1}})=2.922\times {{10}^{-19}}J\] 

13. What is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 4 to an energy level with n =2?

Ans: The ${{n}_{i}}=4$ to ${{n}_{f}}=2$ transition will rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation,

\[E=2.18\times {{10}^{-18}}\left[ \frac{1}{{{n}_{i}}}-\frac{1}{{{n}_{f}}} \right]\] 

Substituting the values in the given expression of E,

\[E=2.18\times {{10}^{-18}}\left[ \frac{1}{{{n}_{i}}^{2}}-\frac{1}{{{n}^{2}}_{f}} \right]=2.18\times {{10}^{-18}}\left[ \frac{1}{{{4}^{2}}}-\frac{1}{{{2}^{2}}} \right]=-4.0875\times {{10}^{-19}}J\] 

The negative sign indicates the energy of emission.

Wavelength of light emitted, \[\lambda =\frac{hc}{E}\] 

Substituting the values in the given expression of \[\lambda \] :

\[\lambda =\frac{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}{4.0875\times {{10}^{-19}}}\] 

\[\lambda =4.8631\times {{10}^{-7}}m\] 

\[\lambda =486nm\] 

14. How much energy is required to ionize a H atom if the electron occupies n = 5 orbit? Compare your answer with the ionization enthalpy of the H atom (energy required to remove the electron from n =1 orbit).

Ans: The expression of energy is given by,

\[{{E}_{n}}=\frac{-(2.18\times {{10}^{-18}}){{Z}^{2}}}{{{n}^{2}}}\] 

Where, Z = atomic number of atom

n = principal quantum number

For ionization from ${{n}_{1}}=5$ to ${{n}_{2}}=\infty $ 

\[\Delta E={{E}_{\infty }}-{{E}_{5}}\] 

\[\Rightarrow \Delta E=\left[ \left( \frac{(-2.18\times {{10}^{-18}}J)({{1}^{2}})}{{{\infty }^{2}}} \right)-\left( \frac{(-2.18\times {{10}^{-18}}J)({{1}^{2}})}{{{5}^{2}}} \right) \right]=2.18\times {{10}^{-18}}J\] 

Hence, the energy required for ionization from \[{{n}_{1}}=5\] to \[{{n}_{2}}=\infty \] is \[8.72\times {{10}^{20}}J\] 

The energy required for ionization from \[{{n}_{1}}=1\] to \[{{n}_{2}}=\infty\]

\[\Delta E={{E}_{\infty }}-{{E}_{1}}\] 

\[\Rightarrow \Delta E=\left[ \left( \frac{(-2.18\times {{10}^{-18}}J)({{1}^{2}})}{{{\infty }^{2}}} \right)-\left( \frac{(-2.18\times {{10}^{-18}}J)({{1}^{2}})}{{{1}^{2}}} \right) \right]=2.18\times {{10}^{-18}}J\] 

Hence, less energy is required to ionize an electron in the ${{5}^{th}}$  orbital of a hydrogen atom as compared to that in the ground state.

15. What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?

Ans: When the excited electron of an H atom in n = 6 drops to the ground state, the following transitions are possible:

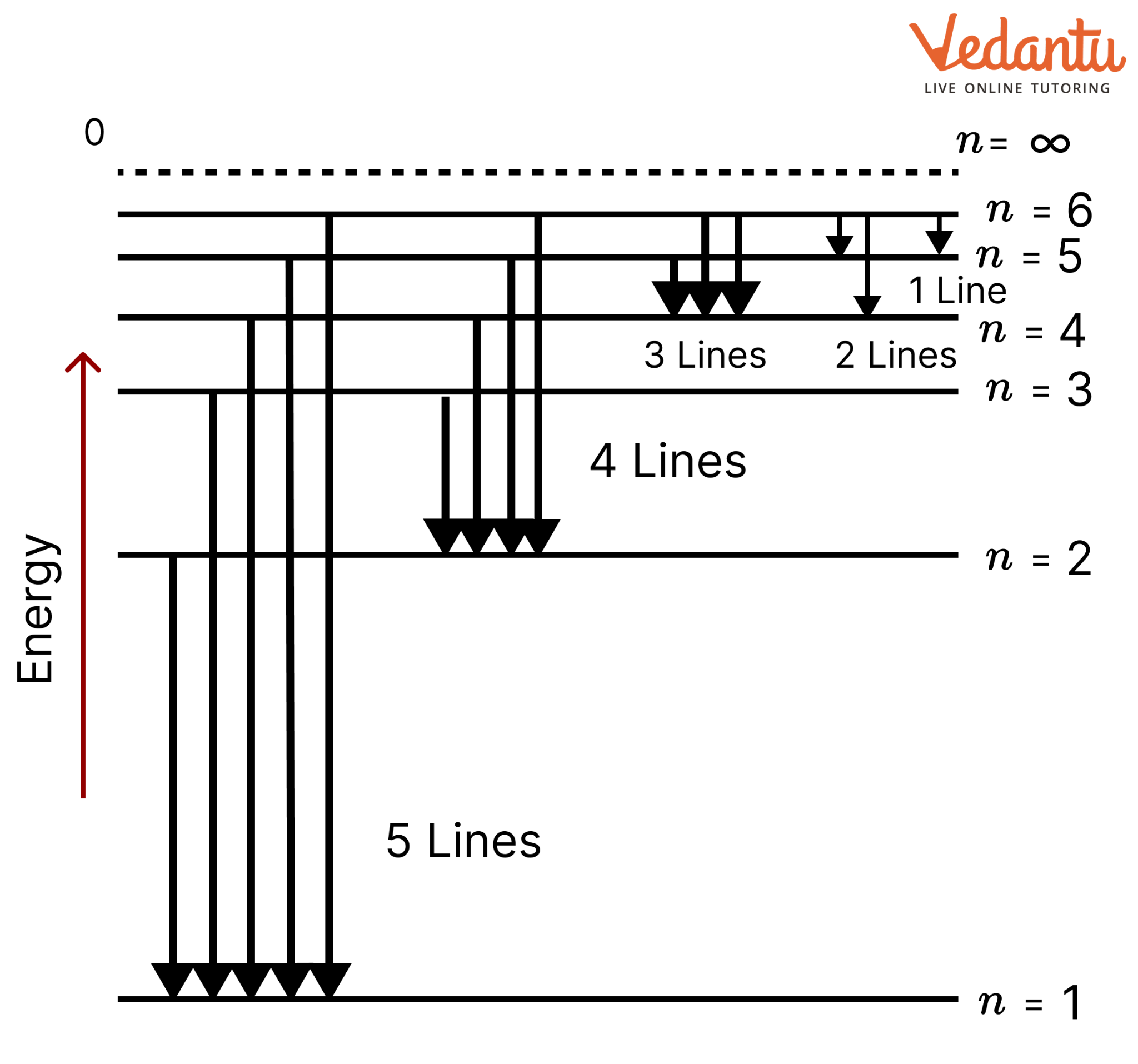
Hence, a total number of (5 + 4 + 3 + 2 + 1) 15 lines will be obtained in the emission spectrum. The number of spectral lines produced when an electron in the ${{n}^{th}}$ level drops down to the ground state is given by. $\frac{n(n-1)}{2}$ 

Number of spectral lines for n=6, $\frac{6(6-1)}{2}=15$ 

16.

(i). The energy associated with the first orbit in the hydrogen atom is $-2.18\times {{10}^{18}}J $&$ ato{{m}^{-1}}$. What is the energy associated with the fifth orbit?

Ans: Energy associated with the fifth orbit of hydrogen atom is calculated as:

\[{{E}_{5}}=\frac{-(2.18\times {{10}^{-18}})}{{{(5)}^{2}}}=\frac{-2.18\times {{10}^{-18}}}{25}\] 

\[{{E}_{5}}=-8.72\times {{10}^{-20}}J\]

(ii). Calculate the radius of Bohr’s fifth orbit for hydrogen atom.

Ans: Radius of Bohr’s ${{n}^{th}}$ orbit for hydrogen atom is given by,

 \[{{r}_{n}}=(0.0529nm){{n}^{2}}\] 

For n = 5,

\[{{r}_{5}}=(0.0529nm)\times {{5}^{2}}\] 

 \[{{r}_{5}}=1.3225nm\] 

17. Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.

Ans: For the Balmer series, ${{n}_{i}}=2$ . Thus, the expression of wave number ($\overset{-}{\mathop{\upsilon }}\,$) is given by

\[\overset{-}{\mathop{\upsilon }}\,=\left( \frac{1}{{{(2)}^{2}}}-\frac{1}{{{n}^{2}}_{f}} \right)(1.097\times {{10}^{7}}{{m}^{-1}})\] 

Wave number ($\overset{-}{\mathop{\upsilon }}\,$) is inversely proportional to wavelength of transition. Hence, for the longest wavelength transition, ($\overset{-}{\mathop{\upsilon }}\,$) has to be the smallest. 

For ($\overset{-}{\mathop{\upsilon }}\,$) to be minimum, ${{n}_{f}}$ should be minimum. For the Balmer series, a transition from ${{n}_{i}}$  = 2 to ${{n}_{f}}$= 3 is allowed. Hence, taking ${{n}_{f}}$ = 3, we get: 

\[\overset{-}{\mathop{\upsilon }}\,=\left( \frac{1}{{{(2)}^{2}}}-\frac{1}{{{(3)}^{2}}} \right)(1.097\times {{10}^{7}}{{m}^{-1}})\] 

\[\overset{-}{\mathop{\upsilon }}\,=\left( \frac{1}{4}-\frac{1}{9} \right)(1.097\times {{10}^{7}}{{m}^{-1}})\] 

 \[\overset{-}{\mathop{\upsilon }}\,=1.5236\times {{10}^{6}}{{m}^{-1}}\] 

18. What is the energy in joules required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state? The ground state electron energy is $-2.18\times {{10}^{-11}}ergs$ 

Ans: Energy (E) of the ${{n}^{th}}$ Bohr orbit of an atom is given by,

 \[{{E}_{n}}=\frac{-(2.18\times {{10}^{-18}}){{Z}^{2}}}{{{n}^{2}}}\] 

Where, Z = atomic number of the atom

Ground state energy=  $-2.18\times {{10}^{-11}}ergs=-2.18\times {{10}^{-11}}\times {{10}^{-7}}J=-2.18\times {{10}^{-18}}J$

Energy required to shift the electron from n = 1 to n = 5 is given as:

\[\Delta E={{E}_{5}}-{{E}_{1}}\] 

 \[=\frac{-(2.18\times {{10}^{-18}}){{(1)}^{2}}}{{{(5)}^{2}}}-(-2.18\times {{10}^{-18}})\] 

\[=(2.18\times {{10}^{-18}})\left( \frac{24}{25} \right)=2.0928\times {{10}^{-18}}\] 

Weight of emitted light = $\frac{hc}{E}$ 

 \[=\frac{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}{(2.0928\times {{10}^{-18}})}=9.498\times {{10}^{-8}}m\] 

19. The electron energy in hydrogen atom is given by ${{E}_{n}}=\frac{(-2.18\times {{10}^{-18}})}{{{n}^{2}}}J$ Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?

Ans: ${{E}_{n}}=\frac{(-2.18\times {{10}^{-18}})}{{{n}^{2}}}J$

Given, 

\[\Delta E={{E}_{\infty }}-{{E}_{2}}\] 

\[\Delta E=\left( \frac{(-2.18\times {{10}^{-18}})}{{{\infty }^{2}}} \right)-\left( \frac{(-2.18\times {{10}^{-18}})}{{{2}^{2}}} \right)=0.545\times {{10}^{-18}}J\] 

Energy required for ionization from n = 2 is given by, \[0.545\times {{10}^{-18}}J\]

 \[\Delta E=5.45\times {{10}^{-19}}J\] 

 \[\lambda =\frac{hc}{\Delta E}\] , here $\lambda $ is the longest wavelength causing the transition.

 \[\lambda =\frac{(6.626\times {{10}^{-34}})(3\times {{10}^{8}})}{5.45\times {{10}^{-19}}}=3.647\times {{10}^{-7}}m\] 

 \[\lambda =3647{{A}^{0}}\] 

20. Calculate the wavelength of an electron moving with a velocity of $2.05\times {{10}^{7}}m{{s}^{-1}}$ 

Ans: According to de Broglie’s equation, $\lambda =\frac{h}{mv}$ 

Where,$\lambda $ = wavelength of moving particle

m = mass of particle, v = velocity of particle, h = Planck’s constant

Substituting the values in the expression of $\lambda $:

\[\lambda =\frac{6.626\times {{10}^{-34}}Js}{(9.10939\times {{10}^{-31}}kg)(2.05\times {{10}^{7}}m{{s}^{-1}})}=3.548\times {{10}^{-11}}m\] 

Hence, the wavelength of an electron moving with a velocity of $2.05\times {{10}^{7}}m{{s}^{-1}}$ is $3.548\times {{10}^{-11}}m$ 

21. The mass of an electron is $9.1\times {{10}^{-31}}kg$ . If it is K.E. is $3.0\times {{10}^{-25}}J$ . Calculate its wavelength.

Ans: According to de Broglie’s equation, $\lambda =\frac{h}{mv}$

Given, the K.E. of electrons is$3.0\times {{10}^{-25}}J$.

Since, $K.E=\frac{1}{2}m{{v}^{2}}$ 

Velocity (v) = $\sqrt{\frac{2K.E}{m}}$ 

\[\Rightarrow v=\sqrt{\frac{2(3.0\times {{10}^{-25}}J)}{9.10939\times {{10}^{-31}}kg}=}\sqrt{6.5866\times {{10}^{4}}}\] 

V= $811.579m{{s}^{-1}}$

 Substituting the value in the expression of $\lambda $ :

\[\lambda =\frac{6.626\times {{10}^{-34}}Js}{(9.10939\times {{10}^{-31}}kg)(811.579m{{s}^{-1}})}\] 

\[\lambda =8.9625\times {{10}^{-7}}m\] 

22. Which of the following are isoelectronic species i.e., those having the same number of electrons? $N{{a}^{+}},{{K}^{+}},M{{g}^{+2}},C{{a}^{+2}},{{S}^{-2}},Ar$ 

Ans: Isoelectronic species have the same number of electrons.

Number of electrons in sodium (Na) = 11

Number of electrons in ($N{{a}^{+}}$) = 10

A positive charge denotes the loss of an electron.

Similarly, 

Number of electrons in ${{K}^{+}}$  = 18 

Number of electrons in $M{{g}^{+2}}$  = 10 

Number of electrons in $C{{a}^{+2}}$  = 18 

A negative charge denotes the gain of an electron by a species. 

Number of electrons in sulphur (S) = 16 

$\therefore $ Number of electrons in ${{S}^{-2}}$  = 18 

Number of electrons in argon (Ar) = 18 

Hence, the following are isoelectronic species: 

(1) $N{{a}^{+}}$and $M{{g}^{+2}}$ (10 electrons each) 

(2) ${{K}^{+}}$,$C{{a}^{+2}}$, ${{S}^{-2}}$and Ar (18 electrons each).

23. 

(i). Write the Electronic Configurations of the Following ions:

(a) ${{H}^{-}}$ ion

Ans: The electronic configuration of H atom is $1{{s}^{1}}$ 

A negative charge on the species indicates the gain of an electron by it.

$\therefore $ Electronic configuration of ${{H}^{-}}$ is $1{{s}^{2}}$ 

(b) $N{{a}^{+}}$ion

Ans: The electronic configuration of Na atom is $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{1}}$ 

A positive charge on the species indicates the loss of an electron by it.

$\therefore $Electronic configuration of $N{{a}^{+}}$is $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{0}}or1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}$ 

(c) ${{O}^{-2}}$ ion

Ans: The electronic configuration of O atom is $1{{s}^{2}}2{{s}^{2}}2{{p}^{4}}$ 

A negative charge on the species indicates the gain of two electrons by it.

$\therefore $Electronic configuration of ${{O}^{-2}}$is $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}$

(d) ${{F}^{-}}$ ion

Ans: The electronic configuration of F atom is $1{{s}^{2}}2{{s}^{2}}2{{p}^{5}}$ 

A negative charge on the species indicates the gain of an electron by it.

$\therefore $Electronic configuration of ${{F}^{-}}$is $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}$

(ii). What are the Atomic Numbers of Elements Whose Outermost Electrons are Represented by 

(a) $3{{s}^{1}}$ 

Ans: Completing the electron configuration of the element as $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{1}}$

$\therefore $ Number of electrons present in the atom of the element 

= 2 + 2 + 6 + 1 = 11

$\therefore $Atomic number of the element = 11

(b) $2{{p}^{3}}$ 

Ans: Completing the electron configuration of the element as $1{{s}^{2}}2{{s}^{2}}2{{p}^{3}}$

$\therefore $ Number of electrons present in the atom of the element 

= 2+2+3=7

$\therefore $Atomic number of the element = 7

(c) $3{{p}^{5}}$ 

Ans: Completing the electron configuration of the element as $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{5}}$

$\therefore $ Number of electrons present in the atom of the element 

= 2+2+6+2+5=17

$\therefore $Atomic number of the element = 17

(iii).Which Atoms are Indicated by the Following Configurations?

(a) $[He]2{{s}^{1}}$ 

Ans: The electronic configuration of the element is $[He]2{{s}^{1}}$= $1{{s}^{2}}2{{s}^{1}}$ 

$\therefore $ Atomic number of the element = 3 

Hence, the element with the electronic configuration $[He]2{{s}^{1}}$is lithium (Li).

(b) $[Ne]3{{s}^{2}}3{{p}^{3}}$

Ans:  The electronic configuration of the element is $[Ne]3{{s}^{2}}3{{p}^{3}}$= $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{3}}$ . 

$\therefore $ Atomic number of the element = 15 

Hence, the element with the electronic configuration $[Ne]3{{s}^{2}}3{{p}^{3}}$is phosphorus (P).

(c) $[Ar]4{{s}^{2}}3{{d}^{1}}$ 

Ans: The electronic configuration of the element is $[Ar]4{{s}^{2}}3{{d}^{1}}$=$1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{1}}$  . 

$\therefore $Atomic number of the element = 21 

Hence, the element with the electronic configuration $[Ar]4{{s}^{2}}3{{d}^{1}}$is scandium (Sc).

24. What is the Lowest Value of n That Allows G Orbitals To Exist?

Ans: For g-orbitals, l = 4. 

As for any value ‘n’ of principal quantum number, the Azimuthal quantum number (l) can have a value from zero to (n – 1). 

$\therefore $ For l = 4, minimum value of n = 5.

25. An Electron Is in One of the 3D Orbitals. Give the Possible Values of n, l and m, for This Electron.

Ans: For the 3d orbital: 

Principal quantum number (n) = 3 

Azimuthal quantum number (l) = 2 

Magnetic quantum number (${{m}_{l}}$) = –2, –1, 0, 1, 2

26. 

(i). An Atom of an Element Contains 29 Electrons and 35 Neutrons. Deduce the Number of Protons.

Ans: For an atom to be neutral, the number of protons is equal to the number of electrons. 

$\therefore $ Number of protons in the atom of the given element = 29

(II). An Atom of an Element Contains 29 Electrons and 35 Neutrons. Deduce the Electronic Configuration of the Given Element.

Ans: The electronic configuration of the atom is $1{{s}^{2}}2{{s}^{2}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{10}}$ 

The name of the element is Copper $_{29}^{35}Cu$ 

27. Give the Number of Electrons in the Species  ${{H}_{2}}^{+}$ , ${{H}_{2}}$ and ${{O}_{2}}^{+}$ 

Ans: ${{H}_{2}}^{+}$:

Number of electrons present in hydrogen molecule (${{H}_{2}}$) = 1 + 1 = 2

$\therefore$Number of electrons in ${{H}_{2}}^{+}$= 2 – 1 = 1

${{H}_{2}}$:

Number of electrons in${{H}_{2}}$ = 1 + 1 = 2

${{O}_{2}}^{+}$:

Number of electrons present in oxygen molecule (${{O}_{2}}$) = 8 + 8 = 16 

$\therefore$ Number of electrons in ${{O}_{2}}^{+}$= 16-1 = 15

28.

(i). An atomic orbital has n = 3. What are the possible values of l and ${{m}_{l}}$ ?

Ans: n = 3 (Given) 

For a given value of n, l can have values from 0 to (n – 1). 

$\therefore$For n = 3 

l = 0, 1, 2 

For a given value of l, ml can have (2l + 1) values. 

$\therefore$For l = 0, m = 0 

l = 1, m = –1, 0, 1 

l = 2, m = –2, –1, 0, 1, 2 

$\therefore$For n = 3 

l = 0, 1, 2 

${{m}_{0}}$ = 0 

${{m}_{1}}$  = –1, 0, 1 

${{m}_{2}}$  = –2, –1, 0, 1, 2

(ii). List the quantum numbers (${{m}_{l}}$ and l) of electrons for 3d orbital.

Ans: For 3d orbital, l = 2. 

For a given value of l, ${{m}_{l}}$ can have (2l + 1) values i.e., 5 values. 

 $\therefore$For l = 2 

${{m}_{2}}$ = –2, –1, 0, 1, 2

(iii). Which of the following orbitals are possible? 

1p, 2s, 2p and 3f

Ans: Among the given orbitals only 2s and 2p are possible. 1p and 3f cannot exist. For p-orbital, l = 1. 

For a given value of n, l can have values from zero to (n – 1). 

Therefore for l is equal to 1, the minimum value of n is 2. 

Similarly, 

For f-orbital, l = 4. 

For l = 4, the minimum value of n is 5. Hence, 1p and 3f do not exist.

29. Using s, p, d notations, describes the orbital with the following quantum numbers.

a)  n = 1, l = 0;

Ans: n = 1, l = 0 (Given) the orbital is 1s.

b)  n = 3; l =1

Ans: For n = 3 and l = 1 the orbital is 3p.

c)  n = 4; l = 2;

Ans: For n = 4 and l = 2 the orbital is 4d.

d)  n = 4; l =3.

Ans: For n = 4 and l = 3 the orbital is 4f.

30. Explain, Giving Reasons, Which of the Following Sets of Quantum Numbers are Not

Ans:

a)  The given set of quantum numbers is not possible because the value of the   principal quantum number (n) cannot be zero.

b)  The given set of quantum numbers is possible.

c)  The given set of quantum numbers is not possible. For a given value of n, ‘l’ can have values from zero to (n – 1). For n = 1, l = 0 and not 1.

d)  The given set of quantum numbers is possible.

e)  The given set of quantum numbers is not possible. For n = 3, 

l = 0 to (3 – 1) 

l = 0 to 2 i.e., 0, 1, 2

f)  The given set of quantum numbers is possible.

31. How Many Electrons in an Atom May Have the Following Quantum Numbers?

a)  n = 4, and ${{m}_{s}}=-\frac{1}{2}$ 

Ans: 

Total number of electrons in an atom for a value of n = $2{{n}^{2}}$ 

$\therefore $ For n = 4,

Total number of electrons = $2{{(4)}^{2}}=32$

The given element has a fully filled orbital as $1{{s}^{2}}2{{s}^{2}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{10}}$ 

Hence, all the electrons are paired. 

$\therefore $ Number of electrons (having n = 4 and ${{m}_{s}}=-\frac{1}{2}$ ) = 16 

b)  n = 3, l = 0

Ans: n = 3, l = 0 indicates that the electrons are present in the 3s orbital. Therefore, the number of electrons having n = 3 and l = 0 is 2.

32. Show That the Circumference of the Bohr Orbit for the Hydrogen Atom is an Integral Multiple of the De Broglie Wavelength Associated With the Electron Revolving Around the Orbit.

Ans: Since a hydrogen atom has only one electron, according to Bohr’s postulate, the angular momentum of that electron is given by:

$mvr=n\frac{h}{2\pi }$ ----------- (i)

Where, n = 1, 2, 3 …

According to de Broglie’s equation:

 $\lambda =\frac{h}{mv}$ Or $mv=\frac{h}{\lambda }$ ------- (ii)

Substituting the value of ‘mv’ from expression (ii) in expression (i):

$\frac{hr}{\lambda }=n\frac{h}{2\pi }$ ----------------- (iii)

Since $2\pi r$  represents the circumference of the Bohr orbit (r), it is proved by equation (iii) that the circumference of the Bohr orbit of the hydrogen atom is an integral multiple of de Broglie’s wavelength associated with the electron revolving around the orbit.

33. What Transition in the Hydrogen Spectrum Would have the Same Wavelength as the Balmer Transition n = 4 to n = 2 of $H{{e}^{+}}$ spectrum?

Ans: for $H{{e}^{+}}$ion, the wave number $\overset{-}{\mathop{v}}\,$ associated with the Balmer transition, n=4 to n =2 given by:

 \[\overset{-}{\mathop{v}}\,=\frac{1}{\lambda }=R{{Z}^{2}}\left( \frac{1}{{{n}_{1}}^{2}}-\frac{1}{{{n}^{2}}_{2}} \right)\] 

Where, ${{n}_{1}}=2and{{n}_{2}}=4$ , Z = atomic number of Helium

  \[\overset{-}{\mathop{v}}\,=\frac{1}{\lambda }=R{{2}^{2}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{4}^{2}}} \right)=\frac{3R}{4}\] 

 \[\Rightarrow \lambda =\frac{4}{3R}\] 

According to the question, the desired transition for hydrogen will have the same wavelength as that of $H{{e}^{+}}$.

\[R{{(1)}^{2}}\left( \frac{1}{{{n}_{1}}^{2}}-\frac{1}{{{n}_{2}}^{2}} \right)=\frac{3R}{4}\] 

 \[\left( \frac{1}{{{n}_{1}}^{2}}-\frac{1}{{{n}_{2}}^{2}} \right)=\frac{3}{4}\] -------- (1)

By hit and trial method, the equality given by equation (1) is true only when ${{n}_{1}}=1$ and ${{n}_{2}}=2$ 

The transition for ${{n}_{2}}=2$to ${{n}_{1}}=1$ in hydrogen spectrum would have the same wavelength as Balmer transition n = 4 to n = 2 of $H{{e}^{+}}$spectrum.

34. Calculate the energy required for the process $H{{e}^{+}}_{(g)}\to H{{e}_{(g)}}^{2+}+{{e}^{-}}$ 

The ionization energy for the H atom in the ground state is $2.18\times {{10}^{-18}}Jato{{m}^{-1}}$ .

Ans: Energy associated with hydrogen-like species is given by,

\[{{E}_{n}}=\frac{-(2.18\times {{10}^{-18}}){{Z}^{2}}}{{{n}^{2}}}\]

For ground state of hydrogen atom,

 \[\Delta E={{E}_{\infty }}-{{E}_{1}}\] 

\[\Rightarrow \Delta E=0-\left[ -2.18\times {{10}^{-18}}\left( \frac{{{(1)}^{2}}}{{{(1)}^{2}}} \right) \right]J\] 

\[\therefore \Delta E=2.18\times {{10}^{-28}}J\] 

For the given process, $H{{e}^{+}}_{(g)}\to H{{e}_{(g)}}^{2+}+{{e}^{-}}$

An electron is removed from n = 1 to n = ∞.

\[\Delta E={{E}_{\infty }}-{{E}_{1}}\]

\[\Rightarrow \Delta E=0-\left[ -2.18\times {{10}^{-18}}\left( \frac{{{(2)}^{2}}}{{{(1)}^{2}}} \right) \right]J\] 

 \[\therefore \Delta E=8.72\times {{10}^{-18}}J\] 

The energy required for the process $8.72\times {{10}^{-18}}J$ 

35. If the Diameter of a Carbon Atom Is 0.15 nm, Calculate the Number of Carbon Atoms Which Can Be Placed Side by Side in a Straight Line Across a Length of Scale of Length 20 cm Long.

Ans: 1 m = 100 cm

1cm = ${{10}^{-2}}m$ 

Length of the scale = 20 cm = $20\times {{10}^{-2}}m$ 

Diameter of a carbon atom = 0.15 nm = $0.15\times {{10}^{-9}}m$ 

One carbon atom occupies $0.15\times {{10}^{-9}}m$

Number of carbon atoms that can be placed in a straight line = \[\frac{20\times {{10}^{-2}}m}{0.15\times {{10}^{-9}}m}=1.33\times {{10}^{9}}\] 

36. $2\times {{10}^{8}}$ atoms of carbon are arranged side by side. Calculate the radius of the carbon atom if the length of this arrangement is 2.4 cm.

Ans: Length of the given arrangement = 2.4 cm

Number of carbon atoms present = $2\times {{10}^{8}}$

$\therefore $ Diameter of carbon atom = $=\frac{2.4\times {{10}^{-2}}}{2\times {{10}^{8}}}=1.2\times {{10}^{-16}}m$ 

Radius of carbon atom = $\frac{diameter}{2}=\frac{1.2\times {{10}^{-10}}m}{2}=6\times {{10}^{-11}}m$ 

37. The diameter of the zinc atom is $2.6{{A}^{0}}$ . 

a)  Calculate radius of zinc atom in pm

Ans: Radius of zinc atom = $\frac{diameter}{2}=\frac{2.6{{A}^{0}}}{2}=1.3\times {{10}^{-11}}m=13\times {{10}^{-12}}m=13pm$ 

b)  Calculate the number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side lengthwise.

Ans: Length of the arrangement = 1.6 cm = $1.6\times {{10}^{-2}}m$ 

Diameter of zinc atom = $2.6{{A}^{0}}$= $2.6\times {{10}^{-10}}m$ 

Number of zinc atoms present in the arrangement =

\[\frac{1.6\times {{10}^{-2}}m}{2.6\times {{10}^{-10}}m}=0.6153\times {{10}^{8}}m\] 

38. A certain particle carries $2.5\times {{10}^{-16}}C$ of static electric charge. Calculate the number of electrons present in it.

Ans: Charge on one electron = $1.6022\times {{10}^{-19}}C$

\[\Rightarrow 1.6022\times {{10}^{-19}}C\] charge is carried by 1 electron.

Number of electrons carrying a charge of $2.5\times {{10}^{-16}}C$

\[=1\left( \frac{2.5\times {{10}^{-16}}C}{1.6022\times {{10}^{-19}}} \right)=1.560\times {{10}^{3}}C=1560C\] 

39. In Milikan’s experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is $-1.282\times {{10}^{-18}}C$ , calculate the number of electrons present in it.

Ans: Charge on the oil drop = $-1.282\times {{10}^{-18}}C$

Charge on one electron = $1.6022\times {{10}^{-19}}C$

$\therefore $ Number of electrons present on the oil drop = $=\frac{1.282\times {{10}^{-18}}C}{1.6022\times {{10}^{-19}}C}=0.8001\times {{10}^{1}}=8.0$ 

40. In Rutherford’s experiment, generally the thin foil of heavy atoms, like gold, platinum etc. have been used to be bombarded by the $\alpha $-particles. If the thin foil of light atoms like aluminium etc. is used, what difference would be observed from the above results?

Ans: A thin foil of lighter atoms will not give the same results as given with the foil of heavier atoms. 

Lighter atoms would be able to carry very little positive charge. Hence, they will not cause enough deflection of $\alpha $-particles (positively charged).  

41. Symbols $_{35}^{79}Br$ and ${}^{79}Br$ can be written. Whereas symbols $_{79}^{35}Br$ and ${}^{35}Br$are not acceptable. Answer briefly.

Ans: The general convention of representing an element along with its atomic mass (A) and atomic number (Z) is $_{Z}^{A}X$ 

Hence, $_{35}^{79}Br$is acceptable, but $_{79}^{35}Br$is not acceptable.

${}^{79}Br$ can be written but ${}^{35}Br$ cannot be written because the atomic number of an element is constant, but the atomic mass of an element depends upon the relative abundance of its isotopes. Hence, it is necessary to mention the atomic mass of an element.

42. An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.

Ans: Let the number of protons in the element be x.

$\therefore $Number of neutrons in the element = $x+0.317x=1.317x$

According to the question, 

Mass number of the element = 81 

(Number of protons + number of neutrons) = 81 

 \[\Rightarrow x+1.317x=81\] 

 \[2.317x=81\] 

  \[x=\frac{81}{2.317}=35\] 

Hence, the number of protons in the element i.e., x is 35. 

Since the atomic number of an atom is defined as the number of protons present in its nucleus, the atomic number of the given element is 35.

The atomic symbol of the element is $_{35}^{81}Br$ 

43. An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than the electrons, find the symbol of the ion.

Ans: Let the number of electrons in the ion carrying a negative charge be x. 

Then, 

Number of neutrons present = $=x+0.111x=1.111x$ 

Number of electrons in the neutral atom = (x – 1) 

(When an ion carries a negative charge, it carries an extra electron) 

$\therefore $ Number of protons in the neutral atom = x – 1

Given,

Mass number of the ion = 37

\[\therefore (x-1)+1.111x=37\] 

 \[2.111x=38\] 

X = 18

Number of electrons = 18; Number of protons = 18 – 1 = 17 

Atomic number of the ion = 17; Atom correspondence to ion = $Cl$ 

$\therefore $The symbol of the ion is ${17}^{37}C{{l}^{-1}}$

44. An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign the symbol to this ion.

Ans: Let the number of electrons present in ion ${{A}^{+3}}$ be ‘x’

Number of neutrons in it = $x+0.304x=1.304x$ 

Since the ion is tripositive,

Number of electrons in neutral atom = x + 3

$\therefore $Number of protons in neutral atom = x + 3

Given, 

Mass number of the ion = 56 

(x + 3) + (1.304x) = 56 

2.304x = 53

x= 23

Number of protons = x + 3 = 23 + 3 = 26

The symbol of the ion ${26}^{56}F{{e}^{3+}}$ 

45. Arrange the Following Type of Radiations in Increasing Order of Frequency:

1. radiation from microwave oven 

2. amber light from traffic signal

3. radiation from FM radio

4. cosmic rays from outer space and

5. X-rays.

Ans: The increasing order of frequency is as follows: 

Radiation from FM radio < amber light < radiation from microwave oven < X- rays < cosmic rays 

The increasing order of wavelength is as follows: 

Cosmic rays < X-rays < radiation from microwave ovens < amber light < radiation of FM radio.

46. Nitrogen laser produces radiation at a wavelength of 337.1 nm. If the number of photons emitted is $5.6\times {{10}^{24}}$ , calculate the power of the laser.

Ans: Power of laser = Energy with which it emits photons

Power = $E=\frac{Nhc}{\lambda }$ 

Where, N = number of photons emitted

h = Planck’s constant

c = velocity of radiation

$\lambda $= wavelength of radiation

Substituting the values in the given expression of E,

\[E=\frac{(5.6\times {{10}^{24}})(6.626\times {{10}^{-34}}Js)(3\times {{10}^{8}}m{{s}^{-1}})}{(337.1\times {{10}^{-9}}m)}=3.33\times {{10}^{6}}J\] 

Hence, the power of laser is $3.33\times {{10}^{6}}J$ 

47. Neon Gas is Generally Used in Sign Boards. If it Emits Strongly at 616 nm,

a)  Calculate the frequency of emission.

Ans: Wavelength of radiation emitted = 616 nm = $616\times {{10}^{-9}}m$ (Given)

Frequency of emission, $v=\frac{c}{\lambda }$ 

Where, c = velocity of radiation

$\lambda =$ Wavelength of radiation

Substituting the values in the given expression of frequency of emission,

\[v=\frac{3.0\times {{10}^{8}}m/s}{616\times {{10}^{-9}}m}=4.87\times {{10}^{14}}{{s}^{-1}}\] 

 Hence, Frequency of emission, $v=4.87\times {{10}^{14}}{{s}^{-1}}$ 

b)  Calculate Distance Traveled by this Radiation in 30 s

Ans: velocity of radiation, c = $3\times {{10}^{8}}m/s$ 

Distance travelled by this radiation in 30 s = $(3\times {{10}^{8}}m{{s}^{-1}})(90s)=9\times {{10}^{9}}m$ 

c)  Calculate energy of quantum…

Ans: energy of Quantum, $E=hv=(6.626\times {{10}^{-34}}Js)(4.87\times {{10}^{14}}{{s}^{-1}})=32.27\times {{10}^{-20}}J$ 

Energy of Quantum (E) = $32.27\times {{10}^{-20}}J$

d)  Calculate number of quanta present if it produces 2 J of energy.

Ans: Energy of one photon (E) = $32.27\times {{10}^{-20}}J$ 

Therefore, $32.27\times {{10}^{-20}}J$ of energy is present in 1 quantum number of quanta in 2J of energy = $\frac{2J}{32.27\times {{10}^{-20}}J}=6.19\times {{10}^{18}}$ 

48.  In astronomical observations, signals observed from distant stars are generally weak. If the photon detector receives a total of $3.15\times {{10}^{-18}}$J from the radiations of 600 nm, calculate the number of photons received by the detector.

Ans: From the expression of energy of one photon, $E=\frac{hc}{\lambda }$ 

Where, $\lambda $ = wavelength of radiation

h = Planck’s constant

c= velocity of radiation

Substituting the values in the given expression of E:

 \[E=\frac{(6.626\times {{10}^{-34}}Js)(3\times {{10}^{8}}m{{s}^{-1}})}{(600\times {{10}^{-9}}m)}\] 

Energy of one photon, E = $3.313\times {{10}^{-19}}J$ 

Number of photons with received with $3.15\times {{10}^{-18}}$J energy,

\[=\frac{3.15\times {{10}^{-18}}J}{3.313\times {{10}^{-19}}J}=9.5\approx 10\] .

Hence, the number of photons received by the detector = 10

49. Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nanosecond range. If the radiation source has a duration of 2 ns and the number of photons emitted during the pulse source is $2.5\times {{10}^{15}}$ , calculate the energy of the source.  

Ans: frequency of radiation, $v=\frac{1}{2.0\times {{10}^{-9}}s}=5\times {{10}^{8}}{{s}^{-1}}$ 

Energy of source, $E=Nhv$ 

Where, N = number of photons emitted

h = Planck’s constant

v = frequency of radiation

Substituting the values in the given expression of E,

$E=(2.5\times {{10}^{15}})(6.626\times {{10}^{-34}}Js)(5.0\times{{10}^{8}}{{s}^{-1}})=8.282\times {{10}^{-10}}J$

Hence, the energy of source, $E=8.282\times {{10}^{-10}}J$

50. The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.

Ans: Given, 

Wavelength associated with first transition, ${{\lambda }_{1}}=589nm=589\times {{10}^{-9}}m$ 

Wavelength associated with second transition, ${{\lambda }_{2}}=589.6nm=589.6\times {{10}^{-9}}m$ 

Frequency of first wavelength is, ${{v}_{1}}=\frac{c}{{{\lambda }_{1}}}=\frac{3\times {{10}^{8}}m{{s}^{-1}}}{589\times {{10}^{-9}}m}=5.093\times {{10}^{14}}{{s}^{-1}}$ 

And, frequency of second wavelength is, ${{v}_{2}}=\frac{c}{{{\lambda }_{2}}}=\frac{3\times {{10}^{8}}m{{s}^{-1}}}{589.6\times {{10}^{-9}}m}=5.088\times {{10}^{14}}{{s}^{-1}}$ 

Energy difference between two excited states is given as,

 \[\Delta E=h{{v}_{1}}-h{{v}_{2}}=h({{v}_{1}}-{{v}_{2}})\] 

\[\Rightarrow \Delta E=(6.626\times {{10}^{-34}}Js)(5.093\times {{10}^{14}}{{s}^{-1}}-5.088\times {{10}^{14}}{{s}^{-1}})=3.31\times {{10}^{-22}}J\] 

51. The Work Function for Cesium Atoms is 1.9 eV.

a)  Calculate the threshold wavelength

Ans: It is given that the work function (${{W}_{0}}$) for caesium atom is 1.9 eV. 

From the expression, ${{W}_{o}}=\frac{hc}{{{\lambda }_{0}}}$ 

We get, ${{\lambda }_{o}}=\frac{hc}{{{W}_{0}}}$ 

Where, ${{\lambda }_{0}}$ = threshold wavelength 

h = Planck’s constant 

c = velocity of radiation

Substituting the values in the given expression of${{\lambda }_{0}}$:

${{\lambda }_{0}}=\frac{(6.626\times {{10}^{-1}}Js)(3.0\times {{10}^{8}}m{{s}^{-1}})}{1.9\times 1.602\times {{10}^{-19}}J}=6.53\times {{10}^{-7}}m$ 

Hence, threshold wavelength ${{\lambda }_{0}}$is 653 nm

b)  Calculate the threshold frequency of the radiation. 

Ans: From the expression, ${{W}_{0}}=h{{v}_{0}}$ 

we get, ${{v}_{0}}=\frac{h}{{{W}_{0}}}$ 

Where, ${{v}_{0}}$ = threshold frequency

h = Planck’s constant

Substituting the values in the given expression of${{v}_{0}}$,

${{v}_{0}}=\frac{1.9\times 1.602\times {{10}^{-19}}J}{6.626\times {{10}^{-34}}Js}=4.593\times {{10}^{14}}{{s}^{-1}}$ 

Hence, the threshold frequency of the radiation, ${{v}_{0}}=4.593\times {{10}^{14}}{{s}^{-1}}$ 

c)  If the cesium element is irradiated with a wavelength 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.

Ans: According to the question: 

Wavelength used in irradiation, $\lambda $ = 500nm

Kinetic energy = $h(v-{{v}_{0}})=hc\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)$ 

\[\Rightarrow K.E=(6.626\times {{10}^{-34}}Js)(3.0\times {{10}^{8}}m{{s}^{-1}})\left( \frac{1}{500\times {{10}^{-9}}m}-\frac{1}{653\times {{10}^{-9}}m} \right)\] 

\[=\frac{(1.9878\times {{10}^{-26}})(153\times {{10}^{9}})}{653\times 500}=9.3149\times {{10}^{-20}}J\] 

Kinetic energy of the ejected photoelectron = $9.3149\times {{10}^{-20}}J$ 

Since, kinetic energy = $\frac{1}{2}m{{v}^{2}}=9.3149\times {{10}^{-20}}J$ 

\[v=\sqrt{\frac{2(9.3149\times {{10}^{-20}}J)}{9.10939\times {{10}^{11}}{{m}^{2}}{{s}^{-2}}}}=4.52\times {{10}^{5}}m{{s}^{-1}}\] 

Hence, the velocity of the ejected photoelectron (v) is $4.52\times {{10}^{5}}m{{s}^{-1}}$

52. Following Results are Observed When Sodium Metal is Irradiated With Different Wavelengths.

a)  Calculate threshold wavelength 

Ans: Assuming the threshold wavelength to be ${{\lambda }_{0}}nm$ , the kinetic energy of the radiation is given as:

\[h(v-{{v}_{0}})=\frac{1}{2}m{{v}^{2}}\] 

Three different equalities can be formed by the given value as:

\[hc\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)=\frac{1}{2}m{{v}^{2}}\] 

\[hc\left( \frac{1}{500\times {{10}^{9}}}-\frac{1}{{{\lambda }_{0}}\times {{10}^{-9}}m} \right)=\frac{1}{2}m{{(2.55\times {{10}^{5}}\times {{10}^{-2}}m{{s}^{-1}})}^{2}}\] 

 $\frac{hc}{{{10}^{-9}}m}\left( \frac{1}{500}-\frac{1}{{{\lambda }_{0}}} \right)=\frac{1}{2}m{{(2.55\times {{10}^{3}}m{{s}^{-1}})}^{2}}$ ---------- (1)

Similarly,

$\frac{hc}{{{10}^{-9}}m}\left( \frac{1}{450}-\frac{1}{{{\lambda }_{0}}} \right)=\frac{1}{2}m{{(3.45\times {{10}^{3}}m{{s}^{-1}})}^{2}}$ -------------- (2)

 $\frac{hc}{{{10}^{-9}}m}\left( \frac{1}{400}-\frac{1}{{{\lambda }_{0}}} \right)=\frac{1}{2}m{{(5.35\times {{10}^{3}}m{{s}^{-1}})}^{2}}$ --------------- (3)

Dividing equation (3) by equation (1):

 \[\frac{\left[ \frac{{{\lambda }_{0}}-400}{400{{\lambda }_{0}}} \right]}{\left[ \frac{{{\lambda }_{0}}-500}{500{{\lambda }_{0}}} \right]}=\frac{{{(5.35\times {{10}^{3}}m{{s}^{-1}})}^{2}}}{{{(2.55\times {{10}^{3}}m{{s}^{-1}})}^{2}}}\] 

  \[\frac{5{{\lambda }_{0}}-2000}{4{{\lambda }_{0}}-2000}={{\left( \frac{5.35}{2.55} \right)}^{2}}=\frac{28.6225}{6.5025}\] 

\[\frac{5{{\lambda }_{0}}-2000}{4{{\lambda }_{0}}-2000}=4.40177\] 

 \[17.6070{{\lambda }_{0}}-5{{\lambda }_{0}}=8803.537-2000\] 

  \[{{\lambda }_{0}}=\frac{6805.537}{12.607}=539.8nm=540nm\] 

Threshold wavelength = 540 nm

b)  Calculate Planck’s constant

Ans: the question is not done due to the incorrect values of velocity given in the question.

53. The Ejection of the Photoelectron From the Silver Metal in the Photoelectric Effect Experiment Can Be Stopped by Applying the Voltage of 0.35 v When the Radiation 256.7 nm Is Used. Calculate the Work Function for Silver Metal.

Ans: From the principle of conservation of energy, the energy of an incident photon (E) is equal to the sum of the work function (${{W}_{0}}$) of radiation and its kinetic energy (K.E.) i.e., $E={{W}_{0}}+K.E$ 

we get, ${{W}_{0}}=E-K.E$ 

Energy of incident photon, $E=\frac{hc}{\lambda }$ 

Where, $\lambda $ = wavelength of radiation

C = velocity of radiation

h = Planck’s constant

Substituting the values in the given expression of E:

\[E=\frac{(6.626\times {{10}^{-34}}Js)(3.0\times {{10}^{8}}m{{s}^{-1}})}{256.7\times {{10}^{-9}}m}=7.744\times {{10}^{-19}}J\] 

 \[E=\frac{7.744\times {{10}^{-19}}}{1.602\times {{10}^{-19}}C}=4.83eV\] 

The potential applied to silver metal changes to kinetic energy (K.E) of the photoelectron. Hence, K.E = 0.35 eV

Work function, ${{W}_{0}}=E-K.E$

\[{{W}_{0}}=4.83eV-0.35eV=4.48eV\] 

54. If the Photon of the Wavelength 150 PM Strikes an Atom and One of Its Inner Bound Electrons Is Ejected Out With a Velocity of $1.5\times {{10}^{7}}m{{s}^{-1}}$ , Calculate the energy with which it is bound to the nucleus

Ans: Energy of incident photon (E) is given by, $E=\frac{hc}{\lambda }$ 

\[E=\frac{(6.626\times {{10}^{-34}}Js)(3.0\times {{10}^{8}}m{{s}^{-1}})}{(150\times {{10}^{-12}}m)}=13.252\times {{10}^{-16}}J\] 

Energy of the electron ejected (K.E) = $\frac{1}{2}{{m}_{e}}{{v}^{2}}$ 

\[=\frac{1}{2}(9.10939\times {{10}^{-31}}kg)(1.5\times {{10}^{7}}m{{s}^{-1}})=1.025\times {{10}^{-16}}J\] 

Hence, the energy with which the electron is bound to the nucleus can be obtained as: = E – K.E

=$13.252\times {{10}^{-16}}J-1.02\times {{10}^{-16}}J=12.227\times {{10}^{-16}}J$ 

  \[=\frac{12.227\times {{10}^{-16}}}{1.602\times {{10}^{-19}}C}=7.6\times {{10}^{3}}eV\] 

The energy with which it is bound to the nucleus is $7.6\times {{10}^{3}}eV$ 

55. Emission Transitions in the Paschen Series end at orbit n = 3 and start from orbit n and can be represented as $v=3.29\times {{10}^{5}}(Hz)\left[ \frac{1}{{{3}^{2}}}-\frac{1}{{{n}^{2}}} \right]$ Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.

Ans: Wavelength of transition = 1285 nm = $1285\times {{10}^{-9}}m$$v=3.29\times {{10}^{5}}(Hz)\left[ \frac{1}{{{3}^{2}}}-\frac{1}{{{n}^{2}}} \right]$

Since, $v=\frac{c}{\lambda }=\frac{3.0\times {{10}^{8}}m{{s}^{-1}}}{1285\times {{10}^{-9}}m}=2.33\times {{10}^{14}}{{s}^{-1}}$ 

Substituting the value of v in the given expression,

$2.33\times {{10}^{14}}=3.29\times {{10}^{5}}(Hz)\left[ \frac{1}{{{3}^{2}}}-\frac{1}{{{n}^{2}}} \right]$ 

\[\Rightarrow \left( \frac{1}{9}-\frac{1}{{{n}^{2}}} \right)=\frac{2.33\times {{10}^{14}}}{3.29\times {{10}^{15}}}\] 

 \[\Rightarrow \frac{1}{{{n}^{2}}}=1.1\times {{10}^{-1}}-0.7082\times {{10}^{-1}}\] 

\[\Rightarrow \frac{1}{{{n}^{2}}}=4.029\times {{10}^{-2}}\] 

\[n=\sqrt{\frac{1}{4.029\times {{10}^{-2}}}}=4.98\approx 5\] 

Hence, for the transition to be observed at 1285 nm, n = 5. The spectrum lies in the infra-red region.

56. Calculate the Wavelength for the emission transition if it starts from the orbit having radius 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.

Ans: The radius of the ${{n}^{th}}$ orbit of hydrogen-like particles is given by,

 \[r=\frac{0.529{{n}^{2}}}{Z}{{A}^{0}}\] 

  \[r=\frac{52.9{{n}^{2}}}{Z}pm\] 

For radius, ${{r}_{1}}=1.3225nm=1.3225\times {{10}^{-9}}m=1322.5pm$ 

 \[{{n}_{1}}^{2}=\frac{{{r}_{1}}Z}{52.9}=\frac{1322.5Z}{52.9}\] Similarly, 

\[{{n}_{2}}^{2}=\frac{211.6Z}{52.9}\] 

             \[\frac{{{n}_{1}}^{2}}{{{n}_{2}}^{2}}=\frac{1322.5}{211.6}=6.25\] \[\frac{{{n}_{1}}}{{{n}_{2}}}=2.5=\frac{25}{10}=\frac{5}{2}\] 

 \[\Rightarrow {{n}_{1}}=5\And {{n}_{2}}=2\] 

Thus, the transition is from the ${{5}^{th}}$  orbit to the ${{2}^{nd}}$  orbit. It belongs to the Balmer series. Wave number ($\overset{-}{\mathop{v}}\,$) for the transition is given by,

 \[=1.097\times {{10}^{7}}\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{5}^{2}}} \right)\] 

   \[=1.097\times {{10}^{7}}\left( \frac{21}{100} \right)=2.303\times {{10}^{6}}{{m}^{-1}}\] 

Wavelength associated with the emission transition is given by,

 \[\lambda =\frac{1}{\overset{-}{\mathop{v}}\,}=\frac{1}{2.303\times {{10}^{6}}{{m}^{-1}}}=0.434\times {{10}^{6}}m=434nm\] 

57. Dual Behavior of Matter Proposed by De Broglie Led to the Discovery of Electron Microscopes Often Used for the Highly Magnified Images of Biological Molecules and Other Types of Material. If the velocity of the electron in this microscope is $1.6\times {{10}^{6}}m{{s}^{-1}}$ , calculate the de Broglie wavelength associated with this electron.

Ans: From de Broglie’s equation, 

\[\lambda =\frac{h}{mv}=\frac{6.626\times {{10}^{-34}}Js}{(9.10939\times {{10}^{-31}}kg)(1.6\times {{10}^{6}}m{{s}^{-1}})}=4.55\times {{10}^{-10}}m=455pm\] 

de Broglie’s wavelength associated with the electron is 455 pm.

58. Similar to Electron Diffraction, Neutron Diffraction Microscope is Also Used for the Determination of the Structure of Molecules. If the Wavelength Used Here is 800 PM, Calculate the Characteristic Velocity Associated With the Neutron

Ans: From de Broglie’s equation,

\[\lambda =\frac{h}{mv}\] 

Then, $v=\frac{h}{m\lambda }$ 

Where, 

v = velocity of particle (neutron) 

h = Planck’s constant 

m = mass of particle (neutron) 

$\lambda $ = wavelength

Substituting the values in the expression of velocity (v),

\[v=\frac{(6.626\times {{10}^{-34}})Kg{{m}^{2}}{{s}^{-1}}}{(1.675\times {{10}^{-27}})(8\times {{10}^{-10}}m)}=\frac{6.626\times {{10}^{3}}}{1.675\times 8}=4.94\times {{10}^{2}}m{{s}^{-1}}=494m{{s}^{-1}}\] 

Velocity associated with the neutron = $494m{{s}^{-1}}$ 

59. If the velocity of the electron in Bohr’s first orbit is $2.19\times {{10}^{6}}m{{s}^{-1}}$ calculate the de Broglie wavelength associated with it.

Ans: From de Broglie’s equation,

\[\lambda =\frac{h}{mv}\]

Where, 

v = velocity of particle (neutron) 

h = Planck’s constant 

m = mass of particle (neutron) 

$\lambda $ = wavelength

Substituting the values in the expression of λ:

\[\lambda =\frac{(6.626\times {{10}^{-34}}Js)}{(9.10939\times {{10}^{-31}}kg)(2.19\times {{10}^{6}}m{{s}^{-1}})}=3.32\times {{10}^{-10}}m=332\times {{10}^{-12}}m=332pm\] 

Wavelength associated with the electron = 332 pm

60. The velocity associated with a proton moving in a potential difference of 1000 V is $4.37\times {{10}^{5}}m{{s}^{-1}}$ . If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.

Ans: From de Broglie’s equation,

\[\lambda =\frac{h}{mv}\]

Substituting the values in the expression,

\[\lambda =\frac{(6.626\times {{10}^{-34}}Js)}{(0.1kg)(4.37\times {{10}^{5}}m{{s}^{-1}})}=1.516\times {{10}^{-38}}m\] 

61. If the position of the electron is measured within an accuracy of +0.002 nm, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is $\frac{h}{4\pi m\times 0.05nm}$ . Is there any problem in defining this value?

Ans: From Heisenberg’s uncertainty principle,

\[\Delta x\times \Delta p=\frac{h}{4\pi }\Rightarrow \Delta p=\frac{1}{\Delta x}\frac{h}{4\pi }\] 

Where, $\Delta x$ = uncertainty in position of the electron

$\Delta p$ = uncertainty in momentum of the electron

Substituting the values in the expression of$\Delta p$,

$\Delta p=\frac{1}{0.002nm}\frac{6.626\times {{10}^{-34}}Js}{4\times 3.14}$ 

$\Rightarrow \Delta p=2.637\times {{10}^{-23}}kgm{{s}^{-1}}$ 

Actual momentum = $\frac{h}{4\pi m\times 0.05nm}$= $\frac{6.626\times {{10}^{-34}}Js}{4\times 3.14\times 5.0\times {{10}^{-11}}m}=1.055\times {{10}^{-24}}kgm{{s}^{-1}}$ 

Since the magnitude of the actual momentum is smaller than the uncertainty, the value cannot be defined.

62. The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. If any of these combination(s) has/have the same energy lists:

1. n = 4, l = 2, ${{m}_{l}}=-2,{{m}_{s}}=-\frac{1}{2}$ 

2. n = 3, l = 2, ${{m}_{l}}=1,{{m}_{s}}=+\frac{1}{2}$ 

3. n = 4, l = 1, ${{m}_{l}}=0,{{m}_{s}}=+\frac{1}{2}$ 

4. n = 3, l = 2, ${{m}_{l}}=-2,{{m}_{s}}=-\frac{1}{2}$ 

5. n = 3, l = 1, ${{m}_{l}}=-1,{{m}_{s}}=+\frac{1}{2}$ 

6. n = 4, l = 1, ${{m}_{l}}=0,{{m}_{s}}=+\frac{1}{2}$ 

Ans: For n = 4 and l = 2, the orbital occupied is 4d. 

For n = 3 and l = 2, the orbital occupied is 3d. 

For n = 4 and l = 1, the orbital occupied is 4p. 

Hence, the six electrons i.e., 1, 2, 3, 4, 5, and 6 are present in the 4d, 3d, 4p, 3d, 3p, and 4p orbitals respectively. 

Therefore, the increasing order of energies is 5(3p) < 2(3d) = 4(3d) < 3(4p) = 6(4p) < 1 (4d).

63.  The bromine atom possesses 35 electrons. It contains 6 electrons in 2p orbital, 6 electrons in 3p orbital and 5 electrons in 4p orbital. Which of these electrons experiences the lowest effective nuclear charge?

Ans: Nuclear charge experienced by an electron (present in a multi-electron atom) is dependent upon the distance between the nucleus and the orbital, in which the electron is present. As the distance increases, the effective nuclear charge also decreases. 

Among p-orbitals, 4p orbitals are farthest from the nucleus of bromine atoms with (+35) charge. Hence, the electrons in the 4p orbital will experience the lowest effective nuclear charge. These electrons are shielded by electrons present in the 2p and 3p orbitals along with the s-orbitals. Therefore, they will experience the lowest nuclear charge.

64. Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge? 

(i)  2s and 3s

Ans: Nuclear charge is defined as the net positive charge experienced by an electron in the orbital of a multi-electron atom. The closer the orbital, the greater is the nuclear charge experienced by the electron(s) in it.

The electron(s) present in the 2s orbital will experience greater nuclear charge (being closer to the nucleus) than the electron(s) in the 3s orbital.

(ii)  4d and 4f

Ans: 4d will experience greater nuclear charge than 4f since 4d is closer to the nucleus.

(iii)  3d and 3p

Ans: 3p will experience greater nuclear charge since it is closer to the nucleus than 3f.

65. The unpaired electrons in Al and Si are present in 3p orbital. Which electrons will experience more effective nuclear charge from the nucleus?

Ans: Nuclear charge is defined as the net positive charge experienced by an electron in a multi-electron atom. 

The higher the atomic number, the higher is the nuclear charge. 

Silicon has 14 protons while aluminium has 13 protons. 

Hence, silicon has a larger nuclear charge of (+14) than aluminium, which has a nuclear charge of (+13). 

Thus, the electrons in the 3p orbital of silicon will experience a more effective nuclear charge than aluminium.

66.  Indicate the number of unpaired electrons

a)  Phosphorous (P) 

Ans: Atomic number = 15

The electronic configuration of P is: $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{3}}$ 

The orbital picture of P can be represented as:

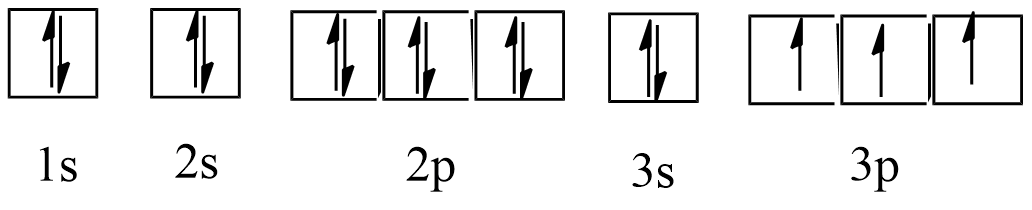
From the orbital picture, phosphorus has three unpaired electrons.

b)  Silicon (Si)

Ans: Atomic number = 14

The electronic configuration of Si is: $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{2}}$

The orbital picture of Si can be represented as:

From the orbital picture, phosphorus has two unpaired electrons.

c)  Chromium (Cr)

Ans: Atomic number = 24

The electronic configuration of Cr is: $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}4{{s}^{1}}3{{d}^{5}}$ 

The orbital picture of chromium is:

From the orbital picture, chromium has six unpaired electrons.

d)  Iron (Fe)

Ans: Atomic number = 26

The electronic configuration is: $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{6}}$ 

The orbital picture of iron is:

From the orbital picture, iron has four unpaired electrons.

e)  Krypton (Kr)

Ans: Atomic number = 36

The electronic configuration is:$1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{10}}4{{p}^{6}}$ 

The orbital picture of krypton is:

Since all orbitals are fully occupied, there are no unpaired electrons in krypton.

67. Answer the following.

a)  How many subshells are associated with n = 4?

Ans: n = 4 (Given) 

For a given value of ‘n’, ‘l’ can have values from zero to (n – 1).

Hence, l = 0, 1, 2, 3

Thus, four subshells are associated with n = 4, which are s, p, d and f.

b)  How many electrons will be present in the sub-shells having ${{m}_{s}}$  value of $-\frac{1}{2}$ for n = 4?

Ans: Number of orbitals in the ${{n}^{th}}$ shell =${{n}^{2}}$ 

for n = 4

Number of orbitals = 16

If each orbital is taken fully, then it will have 1 electron with  ${{m}_{s}}$  value of $-\frac{1}{2}$

$\therefore $ Number of electrons with ${{m}_{s}}$  value of $-\frac{1}{2}$ = 16

Class 11 Chemistry Chapter 2 Quick Overview of Topics

Chemistry class 11 chapter 2 NCERT Solutions -Quick Overview of Detailed Structure of Topics and Subtopics Covered.

Class 11 NCERT solutions Chapter 2 Important Formulas and Concepts 

Class 11 NCERT solutions help the students to go through the formulas and concepts easily. Here find the Important formulas of  Chapter 2 - Structure of Atom to crack your exams.

1. De Broglie's Wavelength Equation:

• $\lambda=\frac{h}{mv}$

2. Heisenberg UNCERTainty Principle:

• $\Delta x \times \Delta p \geq \frac{h}{4\pi}$

• States that it is impossible to simultaneously determine the exact position and momentum of a particle.

3. Quantum Numbers:

• Principal Quantum Number (n): Describes the energy level of an electron in an atom.

• Azimuthal Quantum Number (l): Describes the shape of the orbital.

• Magnetic Quantum Number (m): Describes the orientation of the orbital in space. 

• Spin Quantum Number (ms): Describes the spin of the electron.

4. Aufbau Principle, Pauli's Exclusion Principle, and Hund's Rule:

• Aufbau Principle: Electrons occupy the lowest energy orbitals available.

• Pauli's Exclusion Principle: No two electrons in an atom can have the same set of four quantum numbers.

• Hund's Rule: Electrons occupy orbitals singly before pairing up, and all electrons in singly occupied orbitals have the same spin.

Types of Questions Asked in NCERT solutions class 11 chemistry chapter 2 Structure of Atom

The following are examples of the types of questions asked in the NCERT exercise section for this chapter:

• Fundamental calculations for subatomic particles such as protons, electrons, and neutrons

• Numericals based on the calculating the energy associated with electromagnetic radiation

• Numericals based on the relations between frequency and wavelength

• Problems related to the transition of electrons to different shells

• Questions related to writing the electron configurations

• Problems related to quantum numbers and their combinations for electrons

Benefits of Referring to Vedantu’s NCERT Solutions for class 11 Chemistry Chapter 2 - Structure of Atom

The Vedantu’s class 11 NCERT Solutions of Chemistry Chapter 2 provided here in PDFs offer various benefits, including:

• Comprehensive Coverage: Detailed explanations and step-by-step solutions for all chapter topics.

• Chapter Contents: Galvanic cells, electrolytic cells, Nernst equation, Gibbs free energy, and more.

• Expert Guidance: Solutions curated by experienced educators, ensuring accurate and insightful answers.

• Clarity and Precision: Clear, concise, and easy-to-understand explanations using precise scientific terminology.

• Exam Preparation: Aligned with the latest CBSE syllabus, with practice questions and sample papers.

• Conceptual Understanding: In-depth analysis of key electrochemical concepts and real-life applications.

• Accessibility: Free PDF download for offline access and easy topic navigation.

• Enhanced Problem-Solving Skills: Solutions to a variety of problems to strengthen analytical skills.

Related Study Material Links for Chemistry Class 11 chapter 2 NCERT Solutions 

Students can access extra study materials on Structure of Atom, These resources are available for download, offering additional support for your studies.

Conclusion

You may receive aid comprehending all major ideas from Vedantu specialists, and you can quickly obtain its free PDF online guide on all topics to achieve amazing outcomes in exams. Getting a second view on many issues is really beneficial since sometimes a theory appears simple but is extremely tough to understand. Trusting Vedantu's NCERT solutions class 11 chemistry chapter 2 as a reference is the best option in such instances.

Students may benefit from the availability of class 11 chemistry chapter 2 exercise solutions PDF. These answers include extensive explanations, step-by-step solutions, and key insights into the chapter's themes. Students may improve their comprehension, boost their problem-solving abilities, and thrive in their chemistry studies by using these answers. The ease of use of free PDF downloads allows students to have access to and use these resources for excellent test preparation and general academic achievement.

NCERT Solutions Class 11 Chemistry | Chapter-wise Links 

Access Vedantu’s chapter-wise NCERT Chemistry Class 11 Solutions PDFs below for all other chapters.

Important Links for CBSE Class 11 Chemistry