NCERT Solutions for Class 11 Maths In Hindi Chapter 1 Sets

प्रश्नावली 1.1

1. निम्ननिखित में कौन से समुच्चय हैं? अपिे उत्तर का ओचित्य बताइए।

(i) j अक्षर से होने वाले वर्ष के सभी महीनों का संग्रह। 

उत्तर: j से शुरू होने वाले महीने का नाम है: जनवरी, जून, जुलाई। अतः यह संग्रह एक सेट है। 

(ii) भारत के दस सबसे अधिक प्रतिभाशाली लेखकों का संग्रह।

उत्तर: प्रतिभाशाली एक लेखक को परिभाषित नहीं किया जा सकता। अतः यह संग्रह नहीं है।

(iii) विश्व सर्वक्षरेसठ ग्यारह बल्लेबाजों का संग्रह।

उत्तर: सर्वक्षरेसठ बल्लेबाज को परिभाषित नहीं कर सकते। अतः यह संग्रह नहीं है।

(iv) आपकी कक्षा के सभी बालकों का संग्रह। 

उत्तर: कक्षा के सभी विधीयर्थी के संख्यों निश्चियत होते है। अतः यह संग्रह है।

(v) सों से कम सभी प्राकर्त संख्याओ का संग्रह। 

उत्तर: सों से कम प्रकरत संख्या है। अतः यह संग्रह है।

(vi) लेखक प्रेमचंद द्वारा लिखित उपन्यासों का संग्रह। 

उत्तर: लेखक प्रेमचंद द्वारा लिखित उपन्यासों का संग्रह गबन, गोडाउन आदि द्वारा परिभाषित है। अतः यह संग्रह है।

(vii) सभी संपूर्णको का संग्रह। 

उत्तर: संपूर्णको है। अतः यह एक संग्रह है।

(viii) इस अध्याय मे आने वाले प्रश्नों का संग्रह। 

उत्तर: इस अध्याय के प्रशन प्रभाषित है। अतः यह एक संग्रह है।

(ix) विश्व के सबसे अधिक खतरनाक जानवरों का संग्रह। 

उत्तर: संसार के सबसे अधिक खतरनाक पशुओ के संग्रह को परिभाषित नहीं किया जा सकता। अतः यह एक संग्रह है।

2. मान लीजिए A = \[\{ 1,2,3,4,5,6\} \] रिक्त स्थानों मे उपउक्त प्रतीक \[ \in \;,\; \notin \] भरिए। 

(i) \[5\] ______A

उत्तर: \[5\] \[ \in \] A

(ii) \[8\] ______A

उत्तर: \[8\] \[ \notin \] A

(iii) \[0\] ______A

उत्तर: \[0\] \[ \notin \] A

(iv) \[4\] ______A

उत्तर: \[4\] \[ \in \] A

(v) \[2\] ______A

उत्तर: \[2\] \[ \in \] A

(vi) \[10\] ______A

उत्तर: \[10\] \[ \notin \] A

3. निमानलिखित समुच्चयों को रास्टर रूप मे लिखिए:

(i) A = { \[{\text{x}}\] : \[{\text{x}}\] एक पूर्णक है और \[{\text{ - 3  <  x  <  7}}\] }

उत्तर: A = \[\{  - 2, - 1,0,1,2,3,4,5,6\} \]

(ii) B = { \[{\text{x}}\] : \[{\text{x}}\] संखयश \[{\text{6}}\] से काम एक प्राकरत संख्या है }

उत्तर: B = \[\{ 1,2,3,4,5\} \]

(iii) C = { \[{\text{x}}\] : \[{\text{x}}\] दो अंकों की ऐसी प्राकरत है जिसके अंकों का योगफल आठ है }

उत्तर: C = \[\{ 17,26,35,44,53,62,71,80\} \]

(iv) D = { \[{\text{x}}\] : \[{\text{x}}\] एक अभाग्य संखयश है जो \[{\text{60}}\] की भाजक है }

उत्तर: D = \[\{ 2,3,5\} \]

(v) E = TRIGNOMETRY शब्द के सभी के सभी अक्षरों का समुच्चय। 

उत्तर: E = {T,R,I,G,O,N,M,E,Y}

(vi) F = BETTER शब्द के सभी अक्षरों का समुच्चय। 

उत्तर: F = {B,E,T,E}

4. निमानलिखित समुच्चयों को समुच्चय निर्माण रूप मे वयकेत कीजिए:

(i) \[{\text{\{ 3,6,9,12\} }}\] 

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\;{\text{ = }}\;{\text{3}}\;{\text{n}}\;,\;1\; \leqslant \;{\text{n}}\; \leqslant \;4\} \]

(ii) \[{\text{\{ 2,4,8,16,32\} }}\] 

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\;{\text{ = }}\;{2^{n}},\;1\; \leqslant \;{\text{n}}\; \leqslant \;5\} \]

(iii) \[{\text{\{ 5,25,125,625\} }}\] 

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\;{\text{ = }}\;{5^{n}},,\;1\; \leqslant \;{\text{n}}\; \leqslant \;4\} \]

(iv) \[{\text{\{ 2,4,6,}}...{\text{\} }}\] 

उत्तर: { \[{\text{x}}\;{\text{:}}\;{\text{x}}\] एक सम प्रकरत संख्या है }

(v) \[{\text{\{ 1,4,9,}}...{\text{,100\} }}\] 

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\;{\text{ = }}\;{n^{2}},,\;1\; \leqslant \;{\text{n}}\; \leqslant \;10\} \]

5. निमानलिखित समुच्चय के सभी आवाजय ओकासा को सूचीबद्ध कीजिए:

(i) A = { \[{\text{x}}\] : \[{\text{x}}\] एक विषम लिए प्राकर्त संखयश है}

उत्तर: A = \[{\text{\{ 1,3,5,7\} }}\]

(ii) B = { \[{\text{x}}\] : \[{\text{x}}\] एक पुणक है \[{\text{ - 1/2  <  x  <  9/2}}\] }

उत्तर: B = \[{\text{\{ 0,1,2,3,4\} }}\]

(iii) C = { \[{\text{x}}\] : \[{\text{x}}\] एक पुणक है \[{{\text{x}}^{\text{2}}}\; \leqslant \;4\] }

उत्तर: C = \[{\text{\{  - 2, - 1,0,1,2\} }}\]

(iv) D = { \[{\text{x}}\] : \[{\text{x}}\] लॉइअल शब्द का एक अक्षर है }

उत्तर: D = {L,O,Y,A}

(v) E = { \[{\text{x}}\] : \[{\text{x}}\] वर्ष का एक ऐसा महिना है, जिसमे \[31\] दिन नहीं होते है}  

उत्तर: E = { फरवरी, अप्रैल, जून, सितंबर, नवंबर}

(vi) F = { \[{\text{x}}\] : \[{\text{x}}\] अंग्रेजी वर्णमाला का एक व्यंजन है, जो के: से पहले आता है}

उत्तर: F = {b,c,d,f,g,h,j}

6. बाई और रास्टर रूप मे लिखित और दाई और समुच्चय निर्माण रूप वदत समुच्चयों का सही मिलन कीजिए:

(i) \[\{ 1,2,3,6\} \]            (a) { \[{\text{x}}\]  : \[{\text{x}}\]  एक अभाजय संख्या है और छ: की भाजक है}

(ii) \[\{ 2,3\} \]            (b) { \[{\text{x}}\]  : \[{\text{x}}\]  संख्या \[10\] से कम एक विषम प्राकरत संखयश है}

(iii) {M,A,T,H,E,I,C,S}    (c) { \[{\text{x}}\]  : \[{\text{x}}\]  एक प्राकरत संख्या है और छ: की भाजक है}

(iv) \[\{ 2,3\} \]                (d) { \[{\text{x}}\]  : \[{\text{x}}\]  MATHEMATICS शब्द का एक अक्षर है}

उत्तर : (i) – (c) , (ii) – (a) , (iii) – (d) , (iv) – (b)

प्रश्नावली 1.2 

1. निमानलिखित मे से कौन से रिक्त समुच्चय के उदारण है?

(i) दो से भाज्य विषम प्रकरत संख्याओ का समुच्चयए 

उत्तर: दो से भाज्य कोई भी विषम प्राकर्त संखयाए नहीं है। अतः यह एक रिक्त समुच्चय है।

(ii) सम आभाजी संख्याओ का समुच्चय

उत्तर: सम अभाजय संख्याओ का समुच्चय \[{\text{\{ 2\} }}\] है। अतः यह एक रिक्त समुच्चय नहीं है।

(iii) { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है, \[{\text{x}}\;{\text{ < }}\;{\text{5}}\] और साथ ही साथ \[{\text{x}}\;{\text{ < }}\;7\] }

उत्तर: \[{\text{x}}\;{\text{ < }}\;{\text{5}}\] और साथ ही साथ \[{\text{x}}\;{\text{ < }}\;7\] कोई प्रकरत संख्या नहीं है। अतः यह एक रिक्त समुच्चय है।

(iv) { \[{\text{y}}\] : \[{\text{y}}\] किन्ही भी दो समांतर रेखाओ का उबयनिष्ट बिन्दु है}

उत्तर: समांतर रेखाए कही भी नहीं मिलती है। अतः यह एक रिक्त समुच्चय है।

2. निमानलिखित समुच्चयों मे से कौन परिमित और कौन अपरिमित है 

(i) वर्ष महीनों का समुच्चय 

उत्तर: बर्ष मे बारह महीने होते है। अतः यह एक परिमिति समुच्चय है।

(ii) \[{\text{\{ 1,2,3,}}...{\text{\} }}\]

उत्तर: समुच्चय \[{\text{\{ 1,2,3,}}...{\text{\} }}\] मे अनंत अवयव है। अतः यह एक अपरिमिति समुच्चय है।

(iii) \[{\text{\{ 1,2,3,}}...{\text{,100\} }}\]

उत्तर: समुच्चय\[{\text{\{ 1,2,3,}}...{\text{,100\} }}\] मे कुल सों अवयव हा। अतः यह एक परिमिति समुच्चय है।

(iv) सों से बड़ी धन पूर्णको का समुच्चय 

उत्तर: सों से बड़ा पूर्णको का समुच्चय \[{\text{\{ 101,102,103,}}...{\text{\} }}\] है, जिसमे अनंत अवयव है। अतः यह एक अपरिमिति समुच्चय है।

(v) \[{\text{99}}\] से छोटे अभाजय पूर्णको का समुच्चय 

उत्तर: \[{\text{99}}\] से छोटे अभाज्य पूर्णको समुच्चय \[{\text{\{ 2,3,5,7,}}...{\text{,97\} }}\] है, जिसमे अवयव की संख्या निश्चित है। अतः यह एक अप्रीमिति समुच्चय है।

3. निमानलिखित समुच्चयों मे से प्रत्येक के लिए बताइए कि कौन परिमिति है और कौन अपरिमिति है 

(i) x- अक्ष के समांतर रेखाओ का समुच्चय 

उत्तर: x- अक्ष के समांतर अनंत रेखाओ खींची जा सकती है। अतः यह एक अपरिमिति समुच्चय है।

(ii) अंग्रेजी वर्णमाला के अक्षरों का समुच्चय 

उत्तर: अंग्रेजी वर्णमाला मे कुल \[{\text{26}}\] अक्षर होते है। इन अक्षरों से बनने वाला समुच्चय परिमिति होगा।

(iii) उन संख्याओ का समुच्चय जो पाँच के गुणज है 

उत्तर: पाँच से विभाजित होने वाली संख्याओ का समुच्चय \[{\text{\{ 5,10,15,20,}}...{\text{\} }}\] है, जिसमे अनंत अवयव है। अतः यह एक अपरिमिति समुच्चय है। 

(iv) पृथ्वी पर रहने वाले जानवरों का समुच्चय 

उत्तर: पृथ्वी पर रहने वाले जानवरों का समुच्चय परिमिति होगा। 

(v) मूल बिन्दु \[{\text{(0,0)}}\] से होकर जाने वाले वृतों का समुच्चय 

उत्तर: मूल बिन्दु को केंद्र मानकर अनंत वृत से जा सकता है। अतः यह एक अपरिमिति होगा।

4. निमानलिखित मे बतलाइए कि A = B है अथवा नहीं है 

(i) A = {a,b,c,d} B= {a,c,b,d}

उत्तर: A और b दोनों समुच्चयों के अवयव a,b,c,d है। अतः A = B

(ii) A = \[{\text{\{ 4,8,12,16\} }}\] , B = \[{\text{\{ 8,4,16,18\} }}\]

उत्तर: A मे अवयव बारह है परंतु B मे बही है। अतः A, B के बराबर नहीं है। 

(iii) A = \[{\text{\{ 2,4,6,8,10\} }}\] , B = { \[{\text{x}}\]: \[{\text{x}}\] सम धन पूर्णक है और \[{\text{x}}\;{\text{ < }}\;{\text{10}}\]}

उत्तर: A और B दोनों समुच्चयों के अवयव \[{\text{2,4,6,8,10}}\] है। अतः A = B

(iv) A = { \[{\text{x}}\]: \[{\text{x}}\] संख्याओ दस का गुरणज है }, B = \[{\text{\{ 10,15,20,25,30,}}...{\text{\} }}\]

उत्तर: A = \[{\text{\{ 10,20,30,40,}}...{\text{\} }}\] , B = \[{\text{\{ 10,15,25,30,}}...{\text{\} }}\] , दस के गुरणजों मे \[{\text{5,15,25}}\] नहीं आता है। अतः A, B के बराबर नहीं है।

5. क्या लेखित समुच्चय युगम समान है? कारण सहित बताइए। 

(i) A = \[{\text{\{ 2,3\} }}\] , B = { \[{\text{x}}\] : \[{\text{x}}\] समीकरण \[{{\text{x}}^{\text{2}}}{\text{ + 5x + 6}}\;{\text{ = }}\;{\text{0}}\] का एक हल है }

उत्तर: A = \[{\text{\{ 2,3\} }}\] , B = { \[{\text{x}}\] : \[{\text{x}}\] समीकरण \[{{\text{x}}^{\text{2}}}{\text{ + 5x + 6}}\;{\text{ = }}\;{\text{0}}\] } = \[{\text{\{  - 2, - 3\} }}\] , अतः A और B के अवयव भिन्न है। अतः A, B के बराबर नहीं है।

(ii) A = {\[{\text{k}}\]: \[{\text{x}}\] शब्द FOLLOW का एक अक्षर है } , B = { \[{\text{y}}\]: \[{\text{y}}\] शब्द WOLF का एक अक्षर है }

उत्तर: A = {F,O,L,W}, B = {W,O,L,F}, A और B के अवयव समान है। अतः A = B

6. नीचे दिए हुए समुच्चय मे से समान समुच्चयों का चयन कीजिए:

A = \[{\text{\{ 2,4,8,12\} }}\]

B = \[{\text{\{ 1,2,3,4\} }}\]

C = \[{\text{\{ 4,8,12,14\} }}\]

D = \[{\text{\{ 3,1,4,2\} }}\]

E = \[{\text{\{  - 1,1\} }}\]

F = \[{\text{\{ 0,a\} }}\]

G = \[{\text{\{ 1, - 1\} }}\]

H = \[{\text{\{ 0,1\} }}\]

उत्तर: यह समुच्चय B और D के अवयव \[{\text{1,2,3,4}}\] है B = D, तथा समुच्चय E और G मे अवयव \[{\text{ - 1,1}}\] समान है। अतः E = G

प्रश्नावली 1.3

1. रिक्त स्थानों मे प्रतक \[ \subset \] या \[ \not\subset \] को भर कर सही कथं बनाइये:

(i) \[\{ 2,3,4\} \]______ \[\{ 1,2,3,4,5\} \]

उत्तर: \[\{ 2,3,4\} \]___\[ \subset \] ___ \[\{ 1,2,3,4,5\} \]

(ii) \[{\text{\{ a,b,c\} }}\]______ \[{\text{\{ b,c,d\} }}\]

उत्तर: \[{\text{\{ a,b,c\} }}\]___\[ \not\subset \]___ \[{\text{\{ b,c,d\} }}\]

(iii) {\[{\text{x}}\] : \[{\text{x}}\] आपके विद्यालय का एक विद्यार्थी है}

उत्तर: {\[{\text{x}}\] : \[{\text{x}}\] आपके विद्यालय का एक विद्यार्थी है}____\[ \subset \] 

(iv) {\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक वृत है}____{\[{\text{x}}\] : \[{\text{x}}\] एक समान समतल मे वृत है जिसका त्रिज्या एक इकाई है}

उत्तर: {\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक वृत है}__\[ \not\subset \] __{\[{\text{x}}\] : \[{\text{x}}\] एक समान समतल मे वृत है जिसका त्रिज्या एक इकाई है}

(v) {\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक त्रिभुज है}____{\[{\text{x}}\] : \[{\text{x}}\] किसी संतक मे स्थित एक आयात है}

उत्तर: {\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक त्रिभुज है}__\[ \not\subset \] __{\[{\text{x}}\] : \[{\text{x}}\] किसी संतक मे स्थित एक आयात है}

(vi) {\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक समबाहु त्रिभुज है}____{\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक त्रिभुज है}

उत्तर: {\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक समबाहु त्रिभुज है}__\[ \subset \] __{\[{\text{x}}\] : \[{\text{x}}\] किसी समतल मे स्थित एक त्रिभुज है}

(vii) {\[{\text{x}}\]  : \[{\text{x}}\]  एक सम प्राकरत संख्या है}____{\[{\text{x}}\]  : \[{\text{x}}\]  एक पूर्णक है}

उत्तर: {\[{\text{x}}\]  : \[{\text{x}}\]  एक सम प्राकरत संख्या है}__\[ \subset \] __{\[{\text{x}}\]  : \[{\text{x}}\]  एक पूर्णक है}

2. जाँचिए कि निमानलिखित कथन सत्य है अथवा असत्य है 

(i) \[{\text{\{ a,b\} }}\; \not\subset \;{\text{\{ b,c,a\} }}\]

उत्तर: A = \[{\text{\{ a,b\} }}\] , B = \[{\text{\{ b,c,a\} }}\]

यहा, सेट A का प्रत्येक तत्व सेट B का एक तत्व है 

A \[ \subset \] B

इसलिए, बयान गलत है।

(ii) \[{\text{\{ a,e\} }}\] \[ \subset \] {\[{\text{x}}\] : \[{\text{x}}\] अंग्रेजी वर्णमाला का एक स्वर है}

उत्तर: A = \[{\text{\{ a,e\} }}\] और B = { \[{\text{x}}\] : \[{\text{x}}\] अंग्रेजी वर्णमाला मे एक स्वर है} = \[{\text{\{ a,e,i,o,u\} }}\] 

यहा, सेट A का प्रत्येक तत्व सेट सेट B का एक तत्व है। 

A \[ \subset \] B

इसलिए, कथन सत्य है।

(iii) \[\{ 1,2,3\} \; \subset \;\{ 1,3,5\} \]

उत्तर: A = \[{\text{\{ 1,2,3\} }}\] और B = \[{\text{\{ 1,3,5\} }}\]

यहा, \[{\text{2}}\; \in \]A लेकिन \[{\text{2}}\; \notin \]B

A \[ \not\subset \] B

इसलिए, बयान गलत है।

(iv) \[{\text{\{ a\} }}\; \subset \;{\text{\{ a,b,c\} }}\]

उत्तर: A = \[{\text{\{ a,b\} }}\] और B = \[{\text{\{ a,b,c\} }}\]

यहा, सेट A का प्रत्येक तत्व B का एक तत्व है। 

A \[ \subset \] B

इसलिए, कथन सत्य है।

(v) \[{\text{\{ a,b\} }}\; \in \;{\text{\{ a,b,c\} }}\]

उत्तर:  A = \[{\text{\{ a,b\} }}\]  और B = \[{\text{\{ a,b,c\} }}\]

यहा, \[{\text{\{ a\} }}\; \notin \] B

इसलिए, बयान गलत है। 

(vi) {\[{\text{x}}\] : \[{\text{x}}\] संख्या \[6\] से कम एक सम प्रकरत संख्या है} \[ \subset \] {\[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है, जो संख्या \[36\] को विभाजित करती है}

उत्तर: A = {\[{\text{x}}\] : \[{\text{x}}\] एक समान प्रकरतिक संख्या है जो \[6\]} = \[\{ 2,4\} \] से कम है। 

B = { \[{\text{x}}\] : \[{\text{x}}\] एक प्राकर्तिक संख्या है जो \[36\] } = \[\{ 1,2,3,4,6,12,18,36\} \] को विभाजित करती है। 

यहा, सेट A का प्रत्येक तत्व सेट  B का एक तत्व है। 

A \[ \subset \] B

इसलिए, कथन सत्य है।

3. मान लीजिए कि A = \[\{ 1,2,\{ 3,4\} ,5\} \] निमानलिखित मे से कौन स कथं सही नहीं है और क्यों 

(i) \[\{ 3,4\} \] \[ \subset \] A

उत्तर: \[\{ 3,4\} \] सेट  A का सदस्य है। 

\[\{ 3,4\} \] \[ \in \] A 

इसलिए, \[\{ 3,4\} \] \[ \subset \] A  सही नहीं है।

(ii) \[\{ 3,4\} \] \[ \in \] A

उत्तर: \[\{ 3,4\} \] सेट A के एक सदस्य इसलिए, \[\{ 3,4\}  \in \] A गलत है।

(iii) \[\{ \{ 3,4\} \} \] \[ \subset \] A

उत्तर: \[\{ 3,4\} \] सेट A के एक सदस्य है। 

\[\{ \{ 3,4\} \} \] एक सेट है। 

इसलीये, \[\{ \{ 3,4\} \} \] \[ \subset \] A सही नहीं है।

(iv) \[1\] \[ \in \] A

उत्तर: एक सेट A के एक सदस्य इसलिए  \[1\] \[ \in \] A सही है।

(v) \[1\] \[ \subset \] A

उत्तर: एक सेट, यह इसलिए सेट A के एक सदस्य है नहीं है,  \[1\] \[ \subset \] A सही नहीं है।

(vi) \[\{ 1,2,5\} \] \[ \subset \] A

उत्तर: \[\{ 1,2,5\} \]  सेट A के सदस्य है। 

\[\{ 1,2,5\} \]  सेट A का एक सब्सेट है।  

इसलिए, \[\{ 1,2,5\} \] \[ \subset \] A सही है।

(vii) \[\{ 1,2,5\} \] \[ \in \] A 

उत्तर: \[\{ 1,2,5\} \] सेट A  के सदस्य है। 

\[\{ 1,2,5\} \]  सेट A का सब्सेट है। 

इसलिए, \[\{ 1,2,5\} \]\[ \in \]  A गलत है।

(viii) \[\{ 1,2,3\} \] \[ \subset \] A

उत्तर: \[3\] सेट A  का सदस्य नहीं है। 

\[\{ 1,2,3\} \]  सेट A का सब्सेट नहीं है। 

इसलिए, \[\{ 1,2,3\} \]\[ \subset \]  A सही नहीं है।

(ix) \[\emptyset \] \[ \in \] A

उत्तर: \[\emptyset \]  सेट A के एक सदस्य इसलिए \[\emptyset \] \[ \in \] A सही है नहीं है।

(x) \[\emptyset \] \[ \subset \] A 

उत्तर: \[\emptyset \] सेट A का सदस्य नहीं है इसलिए \[\emptyset \] \[ \subset \] A गलत है।

4. निमानलिखित समुच्चयों के सभी उपसमुच्चय लिखिए: 

(i) \[{\text{\{ a\} }}\]

उत्तर: दिए गए सेट मे तत्वों की संख्या = \[1\]

दिए गए सेट के सब्सेट की संख्या = \[{2^1}\; = \;2\]

इसलिए दिए गए सेट के सब्स्क्रिप्शन है = \[\emptyset \;,\;{\text{\{ a\} }}\]

(ii) \[{\text{\{ a,b\} }}\]

उत्तर: दिए गए सेट मे तत्वों की संख्या = \[2\]

दिए गए सेट के सब्सेट की संख्या = \[{2^2}\; = \;4\]

इसलिए दिए गए सेट के सब्स्क्रिप्शन है = \[\emptyset ,\;{\text{\{ a\} ,}}\;{\text{\{ b\} ,}}\;{\text{\{ a,b\} }}\]

(iii) \[{\text{\{ 1,2,3\} }}\]

उत्तर: दिए गए सेट मे तत्वों की संख्या = \[3\]

दिए गए सेट के सब्सेट की संख्या = \[{2^3}\; = \;8\]

इसलिए दिए गए सेट के सब्स्क्रिप्शन है = \[\emptyset ,\;\{ 1\} ,\;\{ 2\} ,\;\{ 1,2,3\} ,\;\{ 2\} ,\;\{ 3\} ,\;\{ 3,2\} ,\;\{ 3,1\} \]

(iv) \[\emptyset \] 

उत्तर: दिए गए सेट मे तत्वों की संख्या = \[0\]

दिए गए सेट के सब्सेट की संख्या = \[{2^0}\; = \;1\]

इसलिए दिए गए सेट के सब्स्क्रिप्शन है = \[\emptyset \]

5. P(A) के कितने अवयव है, यदि A = \[{\text{0}}\]

उत्तर: सेट A = \[0\] मे तत्वों की संख्या 

दिए गए सेट के सब्सेट की संख्या = \[{2^0}\; = \;1\]

इसलिए, P(A) के तत्वों की संख्या एक है।

6. निमानलिखित को अंतराल रूप मे लिखिए: 

(i) \[{\text{\{ x:x}} \in {\text{R, - 4 < x}} \leqslant {\text{6\} }}\]

उत्तर: A = \[{\text{\{ x:x}} \in {\text{R, - 4 < x}} \leqslant {\text{6\} }}\]

इसे अंतराल के रूप मे लिखा जा सकता है \[( - 4,6]\]

(ii) \[{\text{\{ x:x}} \in {\text{R, - 12 < x}} \leqslant  - 10{\text{\} }}\]

उत्तर: A = \[{\text{\{ x:x}} \in {\text{R, - 12 < x}} \leqslant  - 10{\text{\} }}\]

इसे अंतराल के रूप मे लिखा जा सकता है \[( - 12, - 10)\]

(iii) \[{\text{\{ x:x}} \in {\text{R,0 < x}} \leqslant 7{\text{\} }}\]

उत्तर: A = \[{\text{\{ x:x}} \in {\text{R,0 < x}} \leqslant 7{\text{\} }}\]

इसे अंतराल के रूप मे लिखा जा सकता है \[[0,7)\]

(iv) \[{\text{\{ x:x}} \in {\text{R,3 < x}} \leqslant 4{\text{\} }}\]

उत्तर: A = \[{\text{\{ x:x}} \in {\text{R,3 < x}} \leqslant 4{\text{\} }}\]

इसे अंतराल के रूप मे लिखा जा सकता है \[[3,4]\]

7. निमानलिखित अंतरालों को समुच्चय निर्माण रूप मे लिखिए

(i) \[( - 3,0)\]

उत्तर: \[{\text{\{ x:x}} \in {\text{R, - 3 < x < 0\} }}\]

(ii) \[[6,12]\]

उत्तर: \[{\text{\{ x:x}} \in {\text{R,6}} \leqslant {\text{x}} \leqslant 12{\text{\} }}\]

(iii) \[(6,12]\]

उत्तर: \[{\text{\{ x:x}} \in {\text{R,6 < x}} \leqslant 12{\text{\} }}\]

(iv) \[[ - 23,5)\]

उत्तर: \[{\text{\{ x:x}} \in {\text{R,12}} \leqslant {\text{x}} < 5{\text{\} }}\]

8. निमानलिखित मे से प्रत्येक के लिए आप कौन- सा सार्वत्रिक समुच्चय प्रस्तावित करेंगे 

(i) समकोण त्रिभुजों का समुच्चय 

उत्तर: समकोण त्रिभुज एक प्रकार का त्रिभुज है। इसलिए, त्रिकोण के सेट मे सभी प्रकार के त्रिकोण होते है। 

U = {\[{\text{x}}\] : \[{\text{x}}\] विमान मे एक त्रिकोण है}

(ii) संदिवबहु त्रिभुजों का समुच्चय 

उत्तर: संदिवबहु त्रिभुज का एक प्रकार है। इसलिए त्रिकोण के सेट मे सभी प्रकार के त्रिकोण होते है। 

U = {\[{\text{x}}\] : \[{\text{x}}\] विमान मे एक त्रिकोण है}

9. समुच्चय A = \[\{ 1,3,5\} \] , B = \[\{ 2,4,6\} \] , C = \[\{ 0,2,4,6,8\} \] प्रदत है। इन तीनों समुच्चय A,B,C के लिए निमानलिखित मे से कौन से सार्वत्रिक समुच्चय लिए जा सकते है 

(i) \[\{ 0,1,2,3,4,5,6\} \]

उत्तर: \[\{ 0,1,2,3,4,5,6\} \] है नहीं करने के लिए ए, बी, सी, क्योंकि \[8\; \notin \] C लेकिन \[\{ 0,1,2,3,4,5,6\} \] का सदस्य नहीं है एक सारवबहोमिक सेट।

(ii) \[\emptyset \]

उत्तर: \[\emptyset \] एक ऐसा समुच्चय है जिसमे कोई तत्व नहीं होता है। इसलिए, यह A,B,C के लिए एक सारवबहोमिक सेट नहीं है।

(iii) \[\{ 0,1,2,3,4,5,6,7,8,9,10\} \]

उत्तर: \[\{ 0,1,2,3,4,5,6,7,8,9,10\} \] A,B,C के लिए एक सारवबहोमिक सेट है क्योंकि A,B,C के सभी सदस्य {\[0\] मे मोजूद है, \[1,2,3,4,5,6,7,8,9,10\] }

(iv) \[\{ 1,2,3,4,5,6,7,8\} \]

उत्तर: \[\{ 1,2,3,4,5,6,7,8\} \] A,B,C के लिए एक सारवबहोमिक सेट नहीं है क्योंकि \[0\] C, \[0\] { \[1,2,3,4,4\] का सदस्य नहीं है \[5,6,7,8\] }

प्रश्नावली 1.4 

1. निमानलिखित मे से प्रत्येक समुच्चय युग्म का सम्मिलन ज्ञात कीजिए 

(i) X = \[\{ 1,3,5\} \] , Y = \[\{ 1,2,3\} \]

उत्तर: X \[ \cup \] Y = \[{\text{\{ 1,2,3,5\} }}\]

(ii) A = \[{\text{\{ a,e,i,o,u\} }}\] , B = \[{\text{\{ a,b,c\} }}\]

उत्तर: X \[ \cup \] Y = \[{\text{\{ a,e,i,o,u,b,c\} }}\]

(iii) A = {\[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है और \[{\text{3}}\] का गुणज है}, B = {\[{\text{x}}\] : \[{\text{x}}\] संख्या \[{\text{6}}\] से कम एक प्रकरत संख्या है}

उत्तर: X \[ \cup \] Y = \[{\text{\{ 1,2,3,4,5,6,9,12,15,}}...{\text{\} }}\]

(iv) A = {\[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है और \[{\text{1 < x}} \leqslant {\text{6}}\] }, B = {\[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है और \[6 < {\text{x}} < 10\] }

उत्तर: X \[ \cup \] Y = \[{\text{\{ 2,3,4,5,6,7,8,9\} }}\]

(v) A = \[\{ 1,2,3\} \] , B = \[\emptyset \]

उत्तर: X \[ \cup \] Y = \[{\text{\{ 1,2,3\} }}\]

2. मान लीजिए कि A = \[{\text{\{ a,b\} }}\] , B = \[{\text{\{ a,b,c\} }}\] , क्या A \[ \subset \] B? A \[ \cup \] B ज्ञात कीजिए। 

उत्तर: दिया गया: A = \[{\text{\{ a,b\} }}\] और B = \[{\text{\{ a,b,c\} }}\]

यह सेट A के सभी तत्व सेट B मे मोजूद है। 

A, B और A \[ \cup \] B = \[{\text{\{ a,b,c\} }}\] = B

3. यदि A और B दो ऐसे समुच्चय है कि A \[ \subset \] B तो A \[ \cup \] B क्या है? 

उत्तर: दिया गया: A और B दो सेट है जैसे A \[ \subset \] B 

A = \[\{ 1,2\} \] , B = \[\{ 1,2,3\} \] 

फिर A \[ \cup \] B = \[\{ 1,2,3\} \] = B

4. यदि A = \[\{ 1,2,3,4\} \] , B = \[\{ 3,4,5,6\} \] , C = \[\{ 5,6,7,8\} \] और D = \[\{ 15,17\} \] तो निमानलिखित ज्ञात कीजिए:

(i) A \[ \cup \] B

उत्तर: \[\{ 1,2,3,4,5,6\} \]

(ii) A \[ \cup \] C

उत्तर: \[\{ 1,2,3,4,5,6,7,8\} \]

(iii) B \[ \cup \] C

उत्तर: \[\{ 3,4,5,6,7,8\} \]

(iv) B \[ \cup \] D

उत्तर: \[\{ 3,4,5,6,7,8,9,10\} \]

(v) A \[ \cup \] B \[ \cup \] C

उत्तर: \[\{ 1,2,3,4\} \; \cup \;\{ 3,4,5,6\} \; \cup \;\{ 5,6,7,8\} \]

= \[\{ 1,2,3,4,5,6,7,8\} \]

(vi) A \[ \cup \] B \[ \cup \] D 

उत्तर: \[\{ 1,2,3,4\} \; \cup \;\{ 5,6,7,8\} \; \cup \;\{ 7,8,9,10\} \]

= \[\{ 1,2,3,4,5,6,7,8,9,10\} \]

(vii) B \[ \cup \] C \[ \cup \] D 

उत्तर: \[\{ 3,4,5,6\} \; \cup \;\{ 5,6,7,8\} \; \cup \;\{ 7,8,9,10\} \]

= \[\{ 3,4,5,6,7,8,9,10\} \]

5. प्रशन एक मे दिए गए प्रत्येक समुच्चय युग्म का सर्वनिष्ट समुच्चय ज्ञात कीजिए। 

उत्तर: (i) X \[ \cap \] Y = \[\{ 1,3\} \]

(ii) A \[ \cap \] B = \[{\text{\{ a\} }}\]

(iii) A \[ \cap \] B = \[{\text{\{ 3,6,9,12,}}...{\text{\} }}\]

(iv) A \[ \cap \] B = \[\emptyset \]

(v) A \[ \cap \] B = \[\emptyset \]

6. यदि A = \[\{ 3,5,7,9,11\} \], B = \[\{ 7,9,11,13\} \], C = \[\{ 11,13,15\} \], D = \[\{ 15,17\} \] तो निमानलिखित ज्ञात कीजिए:

(i) A \[ \cap \] B

उत्तर: \[\{ 7,9,11\} \]

(ii) B \[ \cap \] C

उत्तर: \[\{ 11,13\} \]

(iii) A \[ \cap \] C \[ \cap \] D

उत्तर: \[\{ 15\} \]

(iv) A \[ \cap \] C 

उत्तर: \[\{ 11\} \]

(v) B \[ \cap \] D

उत्तर: \[\emptyset \]

(vi) A \[ \cap \] (B \[ \cup \] C)

उत्तर: \[\{ 7,9,11\} \]

(vii) A \[ \cap \] C

उत्तर: \[\emptyset \]

(viii) A \[ \cap \] (B \[ \cup \] D)

उत्तर: \[\{ 7,9,11\} \]

(ix) (A \[ \cap \] B) \[ \cap \] (B \[ \cup \] C) 

उत्तर: \[\{ 7,9,11\} \]

(x) (A \[ \cup \] D) (B \[ \cup \] C)

उत्तर: \[\{ 7,9,11,15\} \]

7. यदि A = { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है}, B = {  \[{\text{x}}\] : \[{\text{x}}\] एक सम प्रकरत संख्या है}, C = {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम प्रकरत संख्या है}, D = {  \[{\text{x}}\] : \[{\text{x}}\] एक अभाज्य संख्या है}, तो निमानलिखित ज्ञात कीजिए:

(i) A \[ \cap \] B

उत्तर: A \[ \cap \]  B = { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है} \[ \cap \]  {  \[{\text{x}}\] : \[{\text{x}}\] एक सम प्रकरत संख्या है} = B

(ii) A \[ \cap \] C

उत्तर: A \[ \cap \] C = { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है} \[ \cap \]  {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम प्रकरत संख्या है} = C

(iii) A \[ \cap \] D

उत्तर: A \[ \cap \] D = { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है}  \[ \cap \]  {  \[{\text{x}}\] : \[{\text{x}}\] एक अभाज्य संख्या है} = D

(iv) B \[ \cap \] C 

उत्तर: B \[ \cap \] C = {  \[{\text{x}}\] : \[{\text{x}}\] एक सम प्रकरत संख्या है} \[ \cap \]   {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम प्रकरत संख्या है} = \[\emptyset \]

(v) B \[ \cap \] D

उत्तर: B \[ \cap \] D = {  \[{\text{x}}\] : \[{\text{x}}\] एक सम प्रकरत संख्या है}  \[ \cap \]  {  \[{\text{x}}\] : \[{\text{x}}\] एक अभाज्य संख्या है}  = \[\{ 2\} \]

(vi) C \[ \cap \] D

उत्तर: C \[ \cap \] D = {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम प्रकरत संख्या है} \[ \cap \]   {  \[{\text{x}}\] : \[{\text{x}}\] एक अभाज्य संख्या है}      = {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम अभाज्य संख्या है}

8. निमानलिखित समुच्चय युग्मों मे से कौन से युग्म असंयुक्त है?

(i) \[\{ 1,2,3,4\} \] तथा { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है और \[4 \leqslant {\text{x}} \leqslant 6\] }

उत्तर: A = \[\{ 1,2,3,4\} \]  , B = { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत संख्या है और}  = \[\{ 4,5,6\} \]

A \[ \cap \] B = \[\{ 4\} \]

इसलिए A और B असन्तुष्ट है।

(ii) \[{\text{\{ a,e,i,o,u\} }}\] तथा \[{\text{\{ c,d,e,f\} }}\] 

उत्तर: A = \[{\text{\{ a,e,i,o,u\} }}\] , B = \[{\text{\{ c,d,e,f\} }}\]

A \[ \cap \] B = \[\emptyset \]

इसलिए A और B असन्तुष्ट है।

(iii) {  \[{\text{x}}\] : \[{\text{x}}\] एक सम पूर्णक है} और {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम पूर्णक है} 

उत्तर: A = {  \[{\text{x}}\] : \[{\text{x}}\] एक सम पूर्णक है} और B = {  \[{\text{x}}\] : \[{\text{x}}\] एक विषम पूर्णक है}

A \[ \cap \] B = \[\emptyset \]

इसलिए A और B असन्तुष्ट है।

9. यदि A = \[{\text{\{ 3,6,9,12,15,18,21\} }}\] , B = \[{\text{\{ 4,8,12,16,20\} }}\] , C = \[{\text{\{ 2,4,6,8,10,12,14,16\} }}\] , D = \[{\text{\{ 5,10,15,20\} }}\] , तो निमानलिखित को ज्ञात कीजिए:

(i) A-B

उत्तर: \[\{ 3,6,9,15,18,21\} \]

(ii) A-C

उत्तर: \[\{ 3,9,15,18,21\} \]

(iii) A-D

उत्तर: \[\{ 3,6,9,15,18,21\} \]

(iv) B-A

उत्तर: \[\{ 4,8,16,20\} \]

(v) C-A

उत्तर: \[\{ 2,4,8,14,16\} \]

(vi) D-A

उत्तर: \[\{ 5,10,20\} \]

(vii) B-C

उत्तर: \[\{ 20\} \]

(viii) B-D

उत्तर: \[\{ 4,8,12,16\} \]

(ix) C-B

उत्तर: \[\{ 2,6,10,14\} \]

(x) D-B

उत्तर: \[\{ 5,10,15\} \]

(xi) C-D

उत्तर: \[\{ 2,4,6,8,12,14,16\} \]

(xii) D-C

उत्तर: \[\{ 5,15,20\} \]

10. यदि X = \[{\text{\{ a,b,c,d\} }}\] और Y = \[{\text{\{ f,b,d,g\} }}\] , तो निमानलिखित को ज्ञात कीजिए: 

(i) X-Y

उत्तर: \[{\text{\{ a,c\} }}\]

(ii) Y-X

उत्तर: \[{\text{\{ f,g\} }}\]

(iii) X \[ \cap \] Y

उत्तर: \[{\text{\{ b,d\} }}\]

11. यदि R वास्तविक संख्याओ और क परिमय संख्याओ के समुच्चय है, तो R-Q क्या होगा?

उत्तर: हम जानते है कि वास्तविक संख्याओ के सेट मे तर्कसंगत और अपरिमय संखयाए होती है। 

इसलिए, = R-Q अपरिमय संख्याओ का सेट।

12. बताइए कि निमानलिखित कथनों मे से प्रत्येक सत्य है या असत्य? अपने उत्तर का ओचित्य भी बताइए: 

(i) \[\{ 2,3,4,5\} \] तथा \[\{ 3,6\} \] संयुक्त समुच्चय है 

उत्तर: A = \[\{ 2,3,4,5\} \] , B = \[\{ 3,6\} \]

A \[ \cap \] B = \[{\text{\{ 3\} }}\]

A और B असन्तुष्ट नहीं है इसलिए बयान गलत है।

(ii) \[{\text{\{ a,e,i,o,u\} }}\] तथा \[{\text{\{ a,b,c,d\} }}\] असंयुक्त समुच्चय है 

उत्तर: A = \[{\text{\{ a,e,i,o,u\} }}\] , B = \[{\text{\{ a,b,c,d\} }}\]

A \[ \cap \] B = \[{\text{\{ a\} }}\]

A और B असन्तुष्ट नहीं है इसलिए बयान गलत है।

(iii) \[{\text{\{ 2,6,10,14\} }}\] तथा \[{\text{\{ 3,7,11,15\} }}\] असंयुक्त समुच्चय है 

उत्तर: A = \[{\text{\{ 2,6,10,14\} }}\] , B = \[{\text{\{ 3,7,11,15\} }}\]

A \[ \cap \] B = \[\emptyset \]

A और B असन्तुष्ट है इसलिए बयान सत्य है।

(iv) \[{\text{\{ 2,6,10\} }}\] तथा \[{\text{\{ 3,7,11\} }}\] असंयुक्त समुच्चय है 

उत्तर: A = \[{\text{\{ 2,6,10\} }}\] , B = \[{\text{\{ 3,7,11\} }}\]

A \[ \cap \] B = \[\emptyset \]

A और B असन्तुष्ट है इसलिए बयान सत्य है।

प्रश्नावली 1.5  

1. मान लीजिए की U = \[\{ 1,2,3,4,5,6,7,8,9\} \] , A = \[\{ 1,2,3,4\} \] , B = \[\{ 2,4,6,8\} \] , C = \[\{ 3,4,5,6\} \] तो निमानलिखित ज्ञात कीजिए:

(i) A’

उत्तर: A’ = U – A = \[\{ 1,2,3,4,5,6,7,8,9\} \] - \[\{ 1,2,3,4\} \] = \[\{ 5,6,7,8,9\} \]

(ii) B’

उत्तर: B’ = U – B = \[\{ 1,2,3,4,5,6,7,8,9\} \] - \[\{ 2,4,6,8\} \] = \[\{ 5,6,7,8,9\} \]

(iii) (A \[ \cup \] C)’

उत्तर: U – (A \[ \cup \] C) = \[\{ 1,2,3,4,5,6,7,8,9\} \] - \[\{ 1,2,3,4,5,6\} \] = \[\{ 7,8,9\} \]

(iv) (A \[ \cup \] B)’

उत्तर: U – (A \[ \cup \] B) = \[\{ 1,2,3,4,5,6,7,8,9\} \] - \[\{ 1,2,3,4,5,6,8\} \] = \[\{ 5,7,9\} \]

(v) (A’)’

उत्तर: U-A = \[\{ 1,2,3,4,5,6,7,8,9\}  - \{ 1,2,3,4\} \]( A’) = \[\{ 5,6,7,8,9\} \] ( A’)

U – A’ = \[\{ 1,2,3,4\} \]

(vi) (B-C)’

उत्तर: U - (B-C) = \[\{ 1,2,3,4,5,6,7,8,9,\}  - \{ 2,8\}  = \{ 1,3,4,5,6,7,9\} \]

2. अगर U = \[{\text{\{ a,b,c,d,e,f,g,h\} }}\] तो निमनलिखित समुच्चयों के पूरक ज्ञात कीजिए 

(i) A = \[{\text{\{ a,b,c\} }}\]

उत्तर: A’ = U – A = \[{\text{\{ a,b,c,d,e,f,g,h\}  - \{ a,b,c\} }}\] = \[{\text{\{ d,e,f,g,h\} }}\]

(ii) B = \[{\text{\{ d,e,f,g\} }}\]

उत्तर: B’ = U – B = \[{\text{\{ a,b,c,d,e,f,g,h\}  - \{ d,e,f,g\} }}\] = \[{\text{\{ a,b,c,h\} }}\]

(iii) C = \[{\text{\{ a,c,e,g\} }}\]

उत्तर: C’ = U – C = \[{\text{\{ a,b,c,d,e,f,g,h\}  - \{ a,c,e,g\} }}\] = \[{\text{\{ b,d,g,h\} }}\]

(iv) D = \[{\text{\{ f,g,h,a\} }}\]

उत्तर: D’ = U – D = \[{\text{\{ a,b,c,d,e,f,g,h\}  - \{ f,g,h,a\} }}\] = \[{\text{\{ b,c,d,e\} }}\]

3. प्रकरत संख्याओ के समुच्चय को सारवित्रीक समुच्चय मानते हुए निमनलिखित समुच्चयों के पूरक लिखिए:

(i) { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत सम संख्या है}

उत्तर: { \[{\text{x}}\] : \[{\text{x}}\] एक विषम प्रकरत संख्या है}

(ii) { \[{\text{x}}\] : \[{\text{x}}\] एक प्रकरत विषम संख्या है}

उत्तर: { \[{\text{x}}\] : \[{\text{x}}\] एक सम संख्या है}

(iii) { \[{\text{x}}\] : \[{\text{x}}\] संख्या तीन का एक धन गुणज है}

उत्तर: { \[{\text{x}}\] : \[{\text{x }} \in \;\mathbb{N}\] संख्या तीन का एक धन गुणज नहीं है}

(iv) { \[{\text{x}}\] : \[{\text{x}}\] एक अभाजय संख्या है}

उत्तर: { \[{\text{x}}\] : \[{\text{x}}\] एक धन भाजय संख्या है}

(v) { \[{\text{x}}\] : \[{\text{x}}\] संख्या तीन और पाँच से विभाजित होने वाली संख्या है}

उत्तर: { \[{\text{x}}\] : \[{\text{x}}\] संख्या तीन और पाँच से विभाजित नहीं होने वाली संख्या है}

(vi) { \[{\text{x}}\] : \[{\text{x}}\] एक पूर्ण वर्ग संख्या है}

उत्तर: { \[{\text{x}}\] : \[{\text{x }} \in \;\mathbb{N}\] तथा \[{\text{x}}\] एक पूर्ण वर्ग धन संख्या नहीं है}

(vii) { \[{\text{x}}\] : \[{\text{x}}\] एक पूर्ण धन संख्या है}

उत्तर: { \[{\text{x}}\] : \[{\text{x }} \in \;\mathbb{N}\] तथा \[{\text{x}}\] एक पूर्ण वर्ग धन संख्या नहीं है}

(viii) \[{\text{\{ x : x + 5  =  8\} }}\]

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\; \in \;\mathbb{N},{\text{x}}\; \ne \;3\} \]

(ix) \[{\text{\{ x : 2x + 5  =  9\} }}\]

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\; \in \;\mathbb{N},{\text{x}}\; \ne \;2\} \]

(x) \[{\text{\{ x : x }} \geqslant {\text{ 7\} }}\]

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\; \in \;\mathbb{N},{\text{x}}\; < \;7\} \]

(xi) \[{\text{\{ x : x}} \in \mathbb{N}{\text{, 2x + 7  >  10\} }}\]

उत्तर: \[\{ {\text{x}}\;{\text{:}}\;{\text{x}}\; \in \;\mathbb{N},{\text{x}}\; < \;\dfrac{9}{2}\} \]

4. यदि U = \[\{ 1,2,3,4,5,6,7,8,9\} \] , A = \[\{ 2,4,6,8\} \] , B = \[\{ 2,3,5,7\} \] तो सत्यापित कीजिए कि

(i) (A \[ \cup \] B)’ = A’ \[ \cap \] B’

उत्तर: A \[ \cup \] B = \[\{ 2,4,6,8\}  - \{ 2,3,5,7\}  = \{ 2,3,4,5,6,7,8\} \]

LHS = (A \[ \cup \] B)’ = U - A \[ \cup \] B = \[\{ 1,2,3,4,5,6,7,8,9\}  - \{ 2,3,4,5,6,7,8\}  = \{ 1,9\} \]

A’ = U – A = \[\{ 1,2,3,4,5,6,7,8,9\}  - \{ 2,4,6,8\}  = \{ 1,3,5,7,9\} \]

B’ = U – B = \[\{ 1,2,3,4,5,6,7,8,9\}  - \{ 2,3,5,7\}  = \{ 1,4,6,8,9\} \]

RHS = A’ \[ \cap \] B’ = \[\{ 1,3,5,7,9\}  \cap \{ 1,4,6,8,9\}  = \{ 1,9\} \]

LHS = RHS

(ii) (A \[ \cap \] B)’ = A’ \[ \cup \] B’

उत्तर: LHS = (A \[ \cap \] B)’ = \[\{ 1,2,3,4,5,6,7,8,9\}  - \{ 2\}  = \{ 1,3,4,5,6,7,8,9\} \]

RHS = A’ \[ \cup \] B’ = \[\{ 1,3,5,7,9\}  \cup \{ 1,4,6,8,9\}  = \{ 1,3,4,5,6,7,8,9\} \]

LHS = RHS

5. निमनलिखित मे प्रत्येक उपयुक्त वेन आरेख खिचिए 

(i) (A \[ \cup \] B)’

उत्तर: 

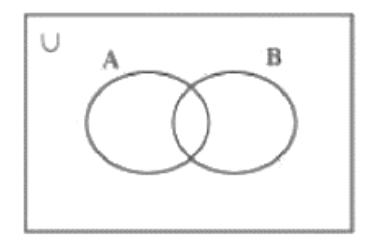
(ii) A’ \[ \cap \] B’ 

उत्तर:

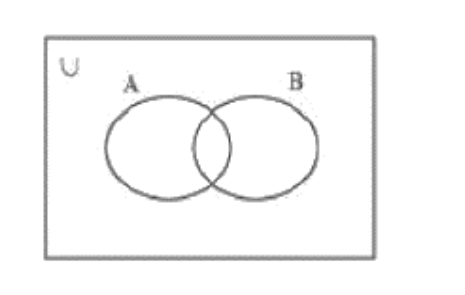
(iii) (A \[ \cap \] B)’ 

उत्तर:

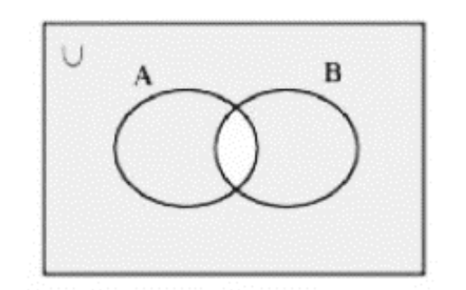
(iv) A’ \[ \cup \] B’ 

उत्तर:

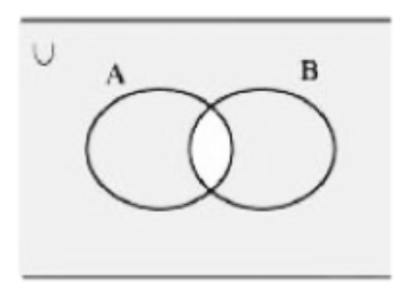
6. मान लीजिए की किसी समतल मे स्थित सभी त्रिभुजों का समुचकी सार्वत्रिक समुच्चय U है। यदि A उन सभी त्रिभुजों का समुच्चय है जिनमे कम से कम एक कोण \[60^\circ \] से भिन्न है तो A’ क्या है। 

उत्तर: U = { \[{\text{x}}\] : समतल मे एक त्रिभुज है}

A = { \[{\text{x}}\] : \[{\text{x}}\] एक त्रिभुजों जिसका कम से कम एक कोण \[60^\circ \] का नहीं हो}

A’ = { सभी समबाहु त्रिभुजों का समुच्चय है}

7. निमनलिखित कथनों को सत्य बनाने के लिए रिक्त स्थानों को भरिए:

(i) (A \[ \cup \] A)’ =.........

उत्तर: U

(ii) \[\emptyset \; \cap \;\] A

उत्तर: U \[ \cup \] A = A

(iii) A \[ \cap \] A’

उत्तर: \[\emptyset \]

(iv) U’ \[ \cap \] A

उत्तर: \[\emptyset \; \cap \;\]A = \[\emptyset \]

प्रश्नावली 1.6

1. यदि X और Y दो ऐसे सानुच्चय हु कि n(X) = \[17\] , n(Y) = \[23\] तथा n(X \[ \cup \] Y) = \[38\] तो 

n(X \[ \cap \] Y) ज्ञात कीजिए। 

उत्तर: दिया गया है,

n(X) = \[17\] , n(Y) = \[23\] तथा n(X \[ \cup \] Y) = \[38\]

n(X \[ \cup \] Y) = n(X) + n(Y) - n(X \[ \cap \] Y)

\[38\] = \[17\] + \[23\] - n(X \[ \cap \] Y) = \[40\] - n(X \[ \cap \] Y)

n(X \[ \cap \] Y) = \[40\] - \[38\] = \[2\]

2. यदि X और Y दो ऐसे समुच्चय है कि X \[ \cup \] Y मे \[18\] , X मे \[8\] और Y मे \[15\] अवयव है तो X \[ \cap \] Y मे कितने अवयव होंगे। 

उत्तर: दिया गया है,

n(X) = \[8\] , n(Y) = \[15\] तथा n(X \[ \cup \] Y) = \[18\]

n(X \[ \cup \] Y) = n(X) + n(Y) - n(X \[ \cap \] Y)

\[18\] = \[8\] + \[15\] - n(X \[ \cap \] Y) = \[23\] - n(X \[ \cap \] Y)

n(X \[ \cap \] Y) = \[23\] - \[18\] = \[5\]

3. \[400\] व्यक्तियों के समूह मे \[250\] हिन्दी तथा \[200\] अंग्रेजी बोल सकते है। कितने व्यक्ति हिन्दी तथा अंग्रेजी दोनों बोल सकते है? 

उत्तर: मान लीजिए की H और E क्रमश: हिन्दी व् अंग्रेजी बोलने वाले लोगों की समुच्चय हो तब 

n(H) = \[250\] , n(E) = \[200\] तथा n(H \[ \cup \] E) = \[400\]

n(H \[ \cup \] E) = n(H) + n(E) - n(H \[ \cap \] E)

\[400\] = \[250\] + \[200\] - n(H \[ \cap \] E) = \[450\] - n(H \[ \cap \] E)

n(H \[ \cap \] E) = \[450\] - \[400\] = \[50\]

4. यदि S और T दो ऐसे समुच्चय है कि S मे \[21\] , T मे \[32\] और  S \[ \cap \] T मे \[11\] अवयव है तो S \[ \cup \] T मे कितने अवयव होंगे।

उत्तर: दिया गया है,

n(S) = \[21\] , n(T) = \[32\] तथा n(S \[ \cap \] T) = \[11\]

n(S \[ \cup \] T) = n(S) + n(T) - n(S \[ \cap \] T)

= \[21\] + \[32\] - \[11\] = \[42\]

5. यदि X और Y दो ऐसे समुच्चय है कि X \[ \cup \] Y मे \[60\] , X मे \[40\] और X \[ \cap \] Y मे \[10\] अवयव है तो Y मे कितने अवयव होंगे। 

उत्तर: दिया गया है,

n(X) = \[40\] , n(X \[ \cap \] Y) = \[10\] तथा n(X \[ \cup \] Y) = \[60\]

n(X \[ \cup \] Y) = n(X) + n(Y) - n(X \[ \cap \] Y)

\[60\] = \[40\] + n(Y) - \[10\] = \[30\] + n(Y)

n(Y) = \[30\]

6. \[70\] व्यक्तियों के समूह मे \[37\] कॉफी, \[52\] चाय पसंद करते है और प्रत्येक व्यक्ति दोनों मे से कम से कम एक पेय पसंद करता है तो कितने व्यक्ति कॉफी और चाय दोनों को पसंद करते है। 

उत्तर: मान लीजिए की C और T क्रमश: कॉफी व् चाय पीने वाले लोगों की समुच्चय हो तब 

n(C) = \[37\] , n(T) = \[52\] तथा n(C \[ \cup \] T) = \[70\]

n(C \[ \cup \] T) = n(C) + n(T) - n(C \[ \cap \] T)

\[70\] = \[37\] + \[52\] - n(C \[ \cap \] T) = \[89\] - n(C \[ \cap \] T)

n(C \[ \cap \] T) = \[89\] - \[70\] = \[19\]

7. \[65\] व्यक्तियों के समूह मे \[40\] व्यक्ति क्रिकेट और \[10\] व्यक्ति क्रिकेट तथा टेनिस दोनों को पसंद करते है तो कितने व्यक्ति केवल टेनिस को पसंद करते होंगे किन्तु क्रिकेट को नहीं? कितने व्यक्ति टेनिस को पसंद करते है। 

उत्तर: मान लीजिए की C और T क्रमश: क्रिकेट व् टेनिस पीने वाले लोगों की समुच्चय हो तब 

n(C) = \[40\] , n(C \[ \cap \] T) = \[10\] तथा n(C \[ \cup \] T) = \[65\]

n(C \[ \cup \] T) = n(C) + n(T) - n(C \[ \cap \] T)

\[65\] = \[40\] + n(T) - \[10\] = \[30\] + n(T)

n(C \[ \cap \] T) = \[65\] - \[30\] = \[35\]

केवल टेनिस को पसंद करने वाले = n(T) - n(C \[ \cap \] T) = \[35\] - \[10\] = \[25\]

8. एक कमेटी मे \[50\] व्यक्ति फ्रेंच, \[20\] व्यक्ति स्पैनिश और \[10\] व्यक्ति स्पैनिश और फ्रेंच दोनों भाषाओ को बोल सकते है। कितने व्यक्ति इन दोनों ही भाषाओ मे से कम से कम एक भाषा बोल सकते है। 

उत्तर: मान लीजिए की F और S क्रमश: फ्रेंच व् स्पैनिश बोलने वाले लोगों की समुच्चय हो तब 

n(F) = \[50\] , n(S) = \[20\] तथा n(F \[ \cap \] S) = \[10\]

n(F \[ \cup \] S) = n(F) + n(S) - n(F \[ \cap \] S)

= \[50\] + \[20\] - \[10\] = \[70\] - \[10\] = \[60\] = कम से कम एक भाषा बोलने वाले

प्रश्नावली A1 

1. निमनलिखित समुच्चयों मे से कौन किसका उपसमुच्चय हैमिस्क निर्णय कीजिए:

A = { \[{\text{x}}\;{\text{:}}\;{\text{x}} \in \mathbb{R},\;{{\text{x}}^{\text{2}}}{\text{ - 8x + 12}}\; = \;0\] को संतुष्ट करने वाली वास्तविक संखयाए \[{\text{x}}\] }, B = \[{\text{\{ 2,4,6\} }}\] , C = \[{\text{\{ 2,4,6,8,}}..{\text{\} }}\] , D = \[{\text{\{ 6\} }}\]

उत्तर: A = { \[{\text{x}}\;{\text{:}}\;{\text{x}} \in \mathbb{R},\;{{\text{x}}^{\text{2}}}{\text{ - 8x + 12}}\; = \;0\] को संतुष्ट करने वाली वास्तविक संखयाए \[{\text{x}}\] } = \[\{ 2,6\} \]

B = \[{\text{\{ 2,4,6\} }}\]

C = \[{\text{\{ 2,4,6,8,}}..{\text{\} }}\]

D = \[{\text{\{ 6\} }}\]

समुच्चय A के अवयव B और C मे भी है। अतः A, B का और C का उपसमुच्चय है,              A \[ \subset \] B, A \[ \subset \] C

समुच्चय B के अवयव C मे है। अतः B, C का उपसमुच्चय है, B \[ \subset \] C

समुच्चय D के अवयव A, B, C मे है। अतः D, A, B, C का उपसमुच्चय है, D \[ \subset \] A, D \[ \subset \] B,                         D \[ \subset \] C

2. ज्ञात कीजिए कि निमनलिखित मे से प्रत्येक कथन सत्य है या असत्य है। यदि सत्य है तो उसे सिद्ध कीजिए। यदि असत्य है तो एक उदाहरण दीजिए। 

(i) यदि \[{\text{x }} \in \;{\text{A}}\] तथा \[{\text{A }} \in \;{\text{B}}\] तो \[{\text{x }} \in \;{\text{B}}\]

उत्तर: मान लेते है कि A = \[\{ 2,4\} \] और B = \[\{ 2,\{ 2,4\} ,8\} \]

परंतु \[4 \notin \{ 2,\{ 2,4\} ,8\} \]

अतः दिया हुआ कथन असत्य है।

(ii) यदि \[{\text{A }} \subset {\text{B}}\] तथा \[{\text{B}} \in {\text{C}}\] तो \[{\text{A}} \in {\text{C}}\]

उत्तर: मान लेते है कि A = \[\{ 2\} \] , B = \[\{ 2,4\} \] और C = \[\{ \{ 2,4\} ,8\} \]

अस्पष्टता \[2 \in \{ 2,4\} {\text{ , }}\{ 2,4\}  \in \{ \{ 2,4\} ,8\} \]

\[{\text{A }} \subset {\text{B}}\] तथा \[{\text{B}} \in {\text{C}}\] 

परंतु \[2 \notin \{ \{ 2,4\} ,8\} \]

A \[ \notin \] C

अतः दिया हुआ कथन असत्य है।

(iii) यदि \[{\text{A }} \subset {\text{B}}\] तथा \[{\text{B}} \subset {\text{C}}\] तो \[{\text{A}} \in {\text{C}}\]

उत्तर: मान लेते है \[{\text{A }} \subset {\text{B}}\] तथा \[{\text{B}} \subset {\text{C}}\]

यदि \[{\text{x}} \in {\text{A}} \Rightarrow {\text{x}} \in {\text{B}}\]

$\Rightarrow {\text{x}} \in {\text{C}} $

$  \therefore {\text{A}} \subset {\text{C}} $

अतः दिया हुआ कथन सत्य है।

(iv) यदि \[{\text{A}} \not\subset {\text{B}}\] तथा \[{\text{B}} \not\subset {\text{C}}\] तो \[{\text{A}} \not\subset {\text{C}}\]

उत्तर: मान लेते है कि \[{\text{A}} = \{ 1,2,3\} ,{\text{B}} = \{ 2,3,4\} ,{\text{C}} \in \{ 1,2,3,8\} \]

स्पष्टता \[{\text{A}} \not\subset {\text{B}}\] तथा \[{\text{B}} \not\subset {\text{C}}\] परंतु \[{\text{A}} \subset {\text{C}}\]

अतः दिया हुआ कथन असत्य है।

(v) यदि \[{\text{x }} \in \;{\text{A}}\] तथा \[{\text{A}} \not\subset {\text{B}}\] तो \[{\text{x }} \in \;{\text{B}}\]

उत्तर: मान लेते है कि \[{\text{A}} = \{ 1,2\} ,\;{\text{B}} = \{ 2,3,4\} \]

स्पष्टता \[{\text{2}} \in {\text{A}}\] और \[{\text{A}} \not\subset {\text{B}}\] और \[{\text{2}} \in {\text{B}}\]

अतः दिया हुआ कथन सत्य है।

(vi) यदि \[{\text{A }} \subset {\text{B}}\] तथा \[{\text{x }} \notin {\text{B}}\] तो \[{\text{x }} \notin {\text{A}}\]

उत्तर: दिया गया है \[{\text{A }} \subset {\text{B}}\] 

यदि \[{\text{x }} \in \;{\text{A}}\] तो \[{\text{x }} \in \;{\text{B}}\]

अतः यदि \[{\text{x }} \notin {\text{A}}\] तो \[{\text{x }} \notin {\text{B}}\] 

अतः दिया हुआ कथन सत्य है।

3. मान लीजिए कि A,B,C ऐसे समुच्चय है कि A \[ \cup \] B = A \[ \cup \] C तथा A \[ \cap \] B = A \[ \cap \] C तो दर्शाइए कि B = C

उत्तर: (A \[ \cup \] B) \[ \cap \] C = (A \[ \cup \] C) \[ \cap \] C = C       [(A \[ \cup \] C) C = C]

(A \[ \cap \] C) \[ \cup \] ( B \[ \cap \] C) = C………………(i)

A \[ \cap \] B = A \[ \cap \] C

(A \[ \cap \] B)  \[ \cap \]  (B \[ \cap \] C) = C

A \[ \cup \] B = A \[ \cup \] C

(A \[ \cup \] B)  \[ \cap \] B = (A \[ \cup \] C) \[ \cap \] B

B = (A \[ \cup \] C) \[ \cap \] B

(A \[ \cap \] B) \[ \cup \] (B \[ \cap \] C) = B……………..(ii)

अतः समीकरण (i) और (ii) से हम यह कह सकते है की B = C

4. दिखाइए कि निमनलिखित चार प्रबंध तुल्य है:

(i) A \[ \subset \] B

उत्तर: A \[ \subset \] B अर्थात के सभी अवयव मे है 

अतः यदि \[{\text{x }} \in \;{\text{A}}\] तो \[{\text{x }} \in \;{\text{B}}\]

A – B = \[\emptyset \]

A \[ \subset \] B, A – B = \[\emptyset \]

(ii) A – B = \[\emptyset \]

उत्तर: अतः \[{\text{x }} \in \;{\text{A}}\] और \[{\text{x }} \in \;{\text{B}}\]

A \[ \subset \] B

(iii) A \[ \cup \] B = B

उत्तर: अगर \[{\text{x }} \in \;{\text{A}}\] तो \[{\text{x }} \in \;{\text{B}}\]

अगर \[{\text{x }} \in \;{\text{B}}\] तो \[{\text{x }} \in \;{\text{A}}\]

A \[ \cup \] B = B

(iv) A \[ \cap \] B = A

उत्तर: अगर \[{\text{x }} \in \;{\text{A}}\] तो \[{\text{x }} \in \;{\text{B}}\]

अगर \[{\text{x }} \in \;{\text{B}}\] तो \[{\text{x }} \in \;{\text{A}}\]

A \[ \cap \] B = A

5. दिखाइए कि यदि A \[ \subset \] B तो C – B \[ \subset \] C – A

उत्तर: मान लेते है कि \[{\text{x}} \in {\text{C}} - {\text{B}} \Rightarrow {\text{x}} \in {\text{C}},{\text{x}} \notin {\text{B}}\]

कि यदि \[{\text{A}} \subset {\text{B}} \Rightarrow {\text{x}} \in {\text{C}},{\text{x}} \notin {\text{A}}\]

\[{\text{x}} \in {\text{C - A}}\] 

स्पष्टता C – B \[ \subset \] C – A

6. मान लीजिए कि P(A) = P(B), सिद्ध कीजिए कि A = B

उत्तर: मान लेते है की \[{\text{x}}\] समुच्चय A का कोई अवयव है 

\[{\text{x}} \in \] A

A \[ \in \] P(A), A \[ \in \] P(B)

यदि C \[ \in \] P(B), \[{\text{x}} \in \] C

C \[ \subset \] B, \[{\text{x}} \in \] B

A \[ \subset \] B, C \[ \subset \] A

A = B

7. किन्ही दो समुच्चय A तथा B के लिए क्या यह सत्य है कि P(A) \[ \cup \] P(B) = P(A \[ \cup \] B), अपने उत्तर का ओचित्य बताइए। 

उत्तर: मान लेते है कि A = \[\{ 1\} \] , B = \[\{ 2\} \] , A \[ \cup \] B = \[\{ 1,2\} \].... (i)

P(A) = \[\{ \emptyset ,\{ 1\} \} \] , P(B) = \[\{ \emptyset ,\{ 2\} \} \]

P(A) \[ \cup \] P(B) = \[\{ \emptyset ,\{ 1\} ,\{ 2\} \} \]

P(A \[ \cup \] B) = \[\{ \emptyset ,\{ 1\} ,\{ 2\} ,\{ 1,2\} \} \]…. (ii) 

अतः समीकरण (i) और (ii) से P(A) \[ \cup \] P(B) \[ \ne \] P(A \[ \cup \] B)

8. किन्ही दो समुच्चय A तथा B के लिए सिद्ध कीजिए कि 

(i) A = (A \[ \cap \] B) \[ \cup \] (A – B)

उत्तर:  (A \[ \cap \] B) \[ \cup \] (A – B) = (A \[ \cap \] B) \[ \cup \] (A \[ \cap \] B’)

= (A \[ \cap \] (B \[ \cup \] B’))  = A

A = (A \[ \cap \] B) \[ \cup \] (A – B)

(ii) A \[ \cup \] (B – A) = A \[ \cup \] B

उत्तर: A \[ \cup \] (B – A) = A \[ \cup \] (B \[ \cap \] A’)

                            = (A \[ \cup \] B)  \[ \cap \] (A \[ \cup \] A’)

                            = (A \[ \cup \] B)  \[ \cap \] U 

                            = A \[ \cup \] B

A \[ \cup \] (B – A) = A \[ \cup \] B

9. समुच्चयों के गुणधर्मों का प्रयोग करके सिद्ध कीजिए कि 

(i) A \[ \cup \] (A \[ \cap \] B) = A

उत्तर: A \[ \cup \] (A \[ \cap \] B) = (A \[ \cup \] A)  \[ \cap \] (A \[ \cup \] B) = A \[ \cap \] (A \[ \cup \] B)

समुच्चय A के सभी अवयव A \[ \cup \] B  मे होंगे अतः A \[ \subset \] (A \[ \cup \] B)

A \[ \cup \] (A \[ \cap \] B) = A

(ii) A \[ \cap \] (A \[ \cup \] B) = A

उत्तर: A \[ \cap \] (A \[ \cup \] B) =  (A \[ \cap \]  A)  \[ \cup \] (A \[ \cap \]  B) = A \[ \cup \]  (A \[ \cap \]  B) 

समुच्चय A के सभी अवयव A \[ \cup \] B  मे होंगे अतः A \[ \subset \] (A \[ \cap \] B)

A \[ \cap \] (A \[ \cup \] B) = A

10. दिखलाइए कि A \[ \cap \] B = A \[ \cap \] C का तात्पर्य B = C आवश्यक रूप से नहीं होता है। 

उत्तर: मान लेते है कि A = \[{\text{\{ a,b\} }}\] , B = \[{\text{\{ a,c\} }}\] , C = \[{\text{\{ a,d\} }}\]

A \[ \cap \] B = \[{\text{\{ a\} }}\] , A \[ \cap \] C = \[{\text{\{ a\} }}\]

तो A \[ \cap \] B = A \[ \cap \] C पर B \[ \ne \] C

11. मान लीजिए कि A और B समुच्चय है। यदि किसी समुच्चय X के लिए A \[ \cap \] X = B \[ \cap \] X = \[\emptyset \] तथा A \[ \cup \] X = B \[ \cup \] X तो सिद्ध कीजिए कि A – B

उत्तर: दिया गया है कि A और B दो समुच्चय है, समुच्चय X के लिए 

A \[ \cap \] X = B \[ \cap \] X = \[\emptyset \] तथा A \[ \cup \] X = B \[ \cup \] X 

हमे ज्ञात है कि A = A \[ \cap \] (A \[ \cup \] X)

A = (A \[ \cap \] A) \[ \cup \] (A \[ \cap \] X)

    = A \[ \cup \] (A \[ \cap \] X) = A \[ \cup \] (B \[ \cap \] X)

    = (A \[ \cup \] B) \[ \cap \] (A \[ \cup \] X) = (A \[ \cup \] B)

B = B \[ \cap \] (B \[ \cup \] X)

   = B \[ \cup \] (B \[ \cap \] X) = B \[ \cup \] (A \[ \cap \] X)

   = (B \[ \cup \] A) \[ \cap \] (B \[ \cup \] X)

   = (B \[ \cup \] A) = (A \[ \cup \] B)

A = B

12. A, B, C ज्ञात कीजिए ताकि A \[ \cap \] B, B \[ \cap \] C, तथा A \[ \cap \] C अरिक्त समुच्चय हो और 

A \[ \cap \] B \[ \cap \] C = \[\emptyset \]

उत्तर: मान लीजिए A = \[{\text{\{ a,b\} }}\] , B = \[{\text{\{ b,c\} }}\] , C = \[{\text{\{ a,c\} }}\]

स्पष्टता A \[ \cap \] B = \[{\text{\{ b\} }}\] , B \[ \cap \] C = \[{\text{\{ c\} }}\] , A \[ \cap \] C = \[{\text{\{ a\} }}\]

परंतु A \[ \cap \] B \[ \cap \] C = (A \[ \cap \] B) \[ \cap \] C = \[{\text{\{ b\} }}\] \[ \cap \] \[{\text{\{ a,c\} }}\] = \[\emptyset \]

13. किसी विद्यालय मे \[600\] विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि \[150\] विद्यार्थी चाय, \[225\] विद्यार्थी कॉफी तथा \[100\] विद्यार्थी चाय और कॉफी दोनों पीते है। ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय और न ही कॉफी पीते है। 

उत्तर: मान लेते है T चाय पीने वाले और C कॉफी पीने वाले विद्यार्थी है

अतः n(T) = \[150\] , n(C) = \[225\] तथा n(T \[ \cap \] C) = \[100\]

n(T \[ \cup \] C) = n(T) + n(C) - n(T \[ \cap \] C)

= \[150\] + \[225\] - \[100\] = \[275\]

जीतने विद्यार्थी न तो चाय और न ही कॉफी पीते है उन विद्यार्थियों की संख्या = \[600 - 275\; = \;325\]

14. विद्यार्थियों के एक समूह मे \[100\] विद्यार्थी हिन्दी, \[50\] विद्यार्थी अंग्रेजी तथा \[25\] विद्यार्थी दोनों भाषाओ को जानते है। विद्यार्थियों मे से प्रत्येक या तो हिन्दी या तो अंग्रेजी जनता है। समूह मे कुल कितने विद्यार्थी है?

उत्तर: मान लेते है H = हिन्दी जानने वाले विद्यार्थियों का समूह , E = अंग्रेजी जानने वाले विद्यार्थियों का समूह 

n(H) = \[100\] , n(E) = \[50\] तथा n(H \[ \cap \] E) = \[25\]

n(H \[ \cup \] E) = n(H) + n(E) - n(H \[ \cap \] E)

= \[100\] + \[50\] - \[25\] = \[125\]

हिन्दी या अंग्रेजी जानने वाले विद्यार्थी की संख्या = \[125\]

15. \[60\] लोगों के सर्वेक्षण मे पाया गया कि \[25\] लोह समाचार पत्र H, \[26\] लोह समाचार पत्र T, \[26\] लोग समाचार पत्र I, \[9\] लोग H तथा I दोनों, \[11\] लोग H तथा T दोनों, \[8\] लोग T  तथा I दोनों और \[3\] लोग तीनों ही समाचार पत्र पड़ते है, तो निमनलिखित ज्ञात कीजिए: 

(i) कम से कम एक समाचार पत्र पड़ने वालों की संख्या 

उत्तर: H समाचार पत्र पड़ने वालों की संख्या, n(H) = \[25\]

T समाचार पत्र पड़ने वालों की संख्या, n(T) = \[26\]

I समाचार पत्र पड़ने वालों की संख्या, n(I) = \[26\]

n(U) = \[60\]

n(H \[ \cap \] I) = \[9\] , n(H \[ \cap \] T) = \[11\] , n(T \[ \cap \] I) = \[8\] , n(H \[ \cap \] T \[ \cap \] I) = \[3\]

n( H T I) = n(H) + n(T) + n(I) - n(H \[ \cap \] I) - n(H \[ \cap \] T) - n(T \[ \cap \] I) + n(H \[ \cap \] T \[ \cap \] I)

= \[25 + 26 + 29 - 9 - 11 - 8 + 3\; = \;52\]

(ii) ठीक- ठीक केवल एक समाचार पत्र पड़ने वालों की संख्या 

उत्तर: केवल H और T पड़ने वालों की संख्या = n(H \[ \cap \] T) - n(H \[ \cap \] T \[ \cap \] I) = \[11 - 3\; = \;8\]

केवल H और I पड़ने वालों की संख्या = n(H \[ \cap \] I) - n(H \[ \cap \] T \[ \cap \] I) = \[9 - 3\; = \;6\]

केवल T और I पड़ने वालों की संख्या = n(T \[ \cap \] I) - n(H \[ \cap \] T \[ \cap \] I) = \[8 - 3\; = \;5\]

केवल एक समाचार पत्र पड़ने वालों की संख्या = \[52 - (8 + 6 + 5 + 3)\; = \;52 - 22\; = \;30\]

16. एक सर्ववेक्षण मे पाया गया कि \[21\] लोग उत्पाद A, \[26\] लोग उत्पाद B, \[29\] लोग उत्पाद C पसंद करते है। यदि \[14\] लोग उत्पाद A तथा B, \[12\] लोग उत्पाद C तथा A, \[14\]  लोग उत्पाद C  तथा B और \[8\] लोग तीनों उत्पादों को पसंद करते है। ज्ञात कीजिए कि कितने केवल उत्पाद C को पसंद करते है। 

उत्तर: उत्पाद A पसंद करने वालों लोगों की संख्या, n(A) = \[21\]

उत्पाद B पसंद करने वालों लोगों की संख्या, n(B) = \[26\]

उत्पाद C पसंद करने वालों लोगों की संख्या, n(C) = \[29\]

N(A \[ \cap \] B) = \[14\] , n(B \[ \cap \] C) = \[14\] , n(A \[ \cap \] C) = \[12\] , n(A \[ \cap \] B \[ \cap \] C) = \[8\]

केवल A और C पसंद करने वालों की संख्या = \[12 - 8\; = \;4\]

केवल B और C पसंद करने वालों की संख्या = \[14 - 8\; = \;6\]

केवल उत्पाद C पसंद करने वालों की संख्या = \[29 - (4 + 6 + 8)\; = \;29 - 18\; = \;11\]

NCERT Solutions for Class 11 Maths Chapter 1 Sets in Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 11 Maths Chapter 1 solution Hindi mediums are created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 11 Maths Chapter 1 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 11 Maths Chapter 1 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 11 Maths Sets solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that.

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 11 Maths Sets in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 11 can download these solutions at any time as per their convenience for self-study purpose.

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/ solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 11 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.