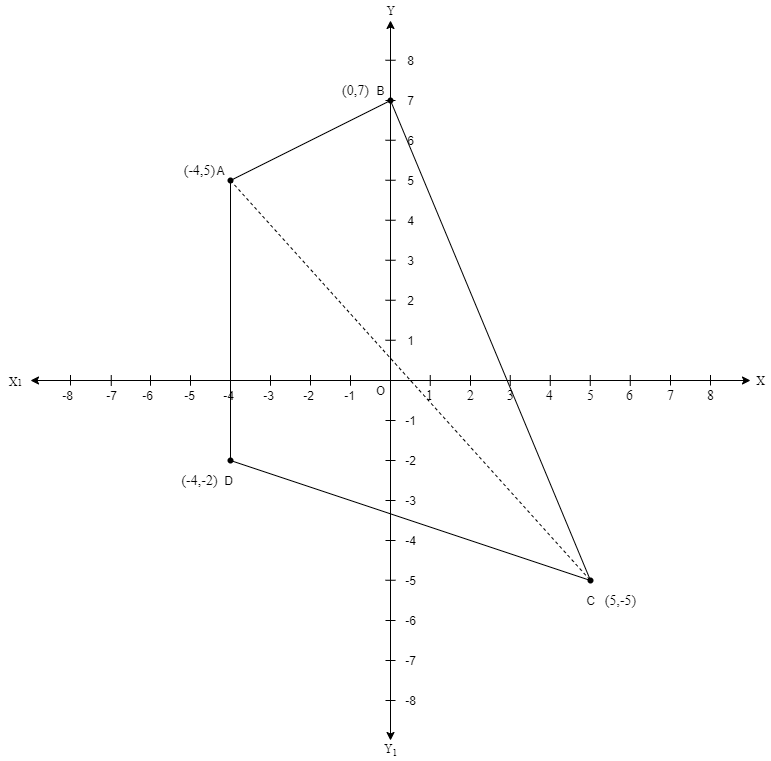
NCERT Solutions for Class 11 Maths Chapter 9: Sequences and Series - Exercise 9.1

Exercise 9.1

1. Write the first five terms of the sequences whose ${{\text{n}}^{\text{th}}}$ term is \[{{\text{a}}_{n}}\text{= n(n+2)}\]. 

Ans:

First we will use the given sequence to find the required terms by putting $\text{n = 1,2,3,4,5}\text{.}$ 

Here we have 

For $\text{n = 1}$

     \[{{\text{a}}_{1}}\text{= 1(1+2)}\] 

\[\Rightarrow {{\text{a}}_{\text{1}}}\text{= 3}\]

For $\text{n = 2}$

     \[{{\text{a}}_{\text{2}}}\text{= 2(2+2)}\]

\[\Rightarrow {{\text{a}}_{\text{2}}}\text{= 8}\]

For $\text{n = 3}$

     \[{{\text{a}}_{\text{3}}}\text{= 3(3+2)}\]

\[\Rightarrow {{\text{a}}_{\text{3}}}\text{= 15}\]

For  $\text{n = 4}$

     \[{{\text{a}}_{\text{4}}}\text{= 4(4+2)}\]

\[\Rightarrow {{\text{a}}_{\text{4}}}\text{= 24}\]

For $\text{n = 5}$

     \[{{\text{a}}_{\text{5}}}\text{= 5(5+2)}\]

\[\Rightarrow {{\text{a}}_{\text{5}}}\text{= 35}\]

Hence the required first five terms of given sequence are $\text{2,8,15,24,35}$ .

2. Write the first five terms of the sequences whose ${{\text{n}}^{\text{th}}}$ term is \[{{\text{a}}_{\text{n}}}\text{=}\frac{\text{n}}{\text{n+1}}\]. 

Ans:

First we will use the given sequence to find the required terms by putting $\text{n = 1,2,3,4,5}\text{.}$ 

Here we have 

For $\text{n = 1}$

\[{{\text{a}}_{\text{1}}}\text{= }\frac{\text{1}}{\text{1+1}}\] 

\[{{\text{a}}_{\text{1}}}\text{= 1}\]

For $\text{n = 2}$

\[{{\text{a}}_{\text{2}}}\text{= }\frac{\text{2}}{\text{2+1}}\]

\[{{\text{a}}_{\text{2}}}\text{= }\frac{\text{2}}{\text{3}}\]

For $\text{n = 3}$

\[{{\text{a}}_{\text{3}}}\text{= }\frac{\text{3}}{\text{3+1}}\]

\[{{\text{a}}_{\text{3}}}\text{= }\frac{\text{3}}{\text{4}}\]

For $\text{n = 4}$

\[{{\text{a}}_{\text{4}}}\text{= }\frac{\text{4}}{\text{4+1}}\]

\[{{\text{a}}_{\text{4}}}\text{= }\frac{\text{4}}{\text{5}}\]

For $\text{n = 5}$

\[{{\text{a}}_{\text{5}}}\text{= }\frac{\text{5}}{\text{5+1}}\]

\[{{\text{a}}_{\text{5}}}\text{= }\frac{\text{5}}{\text{6}}\]

Hence the required first five terms of given sequence are  \[\frac{\text{1}}{\text{2}}\text{,}\frac{\text{2}}{\text{3}}\text{,}\frac{\text{3}}{\text{4}}\text{,}\frac{\text{4}}{\text{5}}\text{,}\frac{\text{5}}{\text{6}}\text{.}\]

3. Write the first five terms of the sequences whose ${{\text{n}}^{\text{th}}}$ term is \[{{\text{a}}_{n}}\text{= }{{\text{2}}^{\text{n}}}\]. 

Ans:

First we will use the given sequence to find the required terms by putting $\text{n = 1,2,3,4,5}\text{.}$ 

Here we have 

For $\text{n = 1}$

\[{{\text{a}}_{\text{1}}}\text{= }{{\text{2}}^{\text{1}}}\] 

\[{{\text{a}}_{\text{1}}}\text{= 2}\]

For $\text{n = 2}$

\[{{\text{a}}_{\text{2}}}\text{= }{{\text{2}}^{\text{2}}}\]

\[{{\text{a}}_{\text{2}}}\text{= 4}\]

For $\text{n = 3}$

\[{{\text{a}}_{\text{3}}}\text{= }{{\text{2}}^{\text{3}}}\]

\[{{\text{a}}_{\text{3}}}\text{= 8}\]

For $\text{n = 4}$

\[{{\text{a}}_{\text{4}}}\text{= }{{\text{2}}^{\text{4}}}\]

\[{{\text{a}}_{\text{4}}}\text{= 16}\]

For  $\text{n = 5}$

\[{{\text{a}}_{\text{5}}}\text{= }{{\text{2}}^{\text{5}}}\]

\[{{\text{a}}_{\text{5}}}\text{= 32}\]

Hence the required first five terms of given sequence are $\text{2,4,8,16,32}\text{.}$ 

4. Write the first five terms of the sequences whose ${{\text{n}}^{\text{th}}}$  term is \[{{\text{a}}_{\text{n}}}\text{= }\frac{\text{2n-3}}{\text{6}}\]. 

Ans: First we will use the given sequence to find the required terms by putting $\text{n = 1,2,3,4,5}\text{.}$ 

Here we have 

For $\text{n = 1}$

\[{{\text{a}}_{\text{1}}}\text{= }\frac{\text{2(1) - 3}}{\text{6}}\] 

\[{{\text{a}}_{\text{1}}}\text{= }\frac{\text{-1}}{\text{6}}\]

For $\text{n = 2}$

\[{{\text{a}}_{\text{2}}}\text{= }\frac{\text{2(2) - 3}}{\text{6}}\]

\[{{\text{a}}_{\text{2}}}\text{= }\frac{\text{1}}{\text{6}}\]

For $\text{n = 3}$

     \[{{\text{a}}_{\text{3}}}\text{= }\frac{\text{2(3) - 3}}{\text{6}}\]

     \[{{\text{a}}_{\text{3}}}\text{= }\frac{\text{3}}{\text{6}}\]

\[\Rightarrow {{\text{a}}_{\text{3}}}\text{= }\frac{\text{1}}{\text{2}}\]

For $\text{n = 4}$

\[{{\text{a}}_{\text{4}}}\text{= }\frac{\text{2(4) - 3}}{\text{6}}\]

\[{{\text{a}}_{\text{4}}}\text{= }\frac{\text{5}}{\text{6}}\]

For $\text{n = 5}$

\[{{\text{a}}_{\text{5}}}\text{= }\frac{\text{2(5) - 3}}{\text{6}}\]

\[{{\text{a}}_{\text{5}}}\text{= }\frac{\text{7}}{\text{6}}\]

Hence the required first five terms of given sequence are  \[\text{-}\frac{\text{1}}{\text{6}}\text{,}\frac{\text{1}}{\text{6}}\text{,}\frac{\text{1}}{\text{2}}\text{,}\frac{\text{5}}{\text{6}}\text{,}\frac{\text{7}}{\text{6}}\text{.}\]

5. Write the first five terms of the sequences whose term is \[{{\text{a}}_{\text{n}}}\text{= (-1}{{\text{)}}^{\text{n-1}}}{{\text{5}}^{\text{n+1}}}\]. 

Ans:

First we will use the given sequence to find the required terms by putting $\text{n = 1,2,3,4,5}\text{.}$ 

Here we have 

For  $\text{n = 1}$

     \[{{\text{a}}_{\text{1}}}\text{=  (-1}{{\text{)}}^{\text{(1-1)}}}{{\text{5}}^{\text{(1+1)}}}\] 

        \[\text{= (-1}{{\text{)}}^{\text{0}}}{{\text{(5)}}^{\text{2}}}\]

\[\Rightarrow {{\text{a}}_{\text{1}}}\text{=  25}\]

For  $\text{n = 2}$

     \[{{\text{a}}_{\text{2}}}\text{= (-1}{{\text{)}}^{\text{(2-1)}}}{{\text{5}}^{\text{(2+1)}}}\]

          \[\text{= (-1}{{\text{)}}^{\text{1}}}{{\text{(5)}}^{\text{3}}}\]

\[\Rightarrow {{\text{a}}_{\text{2}}}\text{= -125}\]

For $\text{n = 3}$

     \[{{\text{a}}_{\text{3}}}\text{= (-1}{{\text{)}}^{\text{(3-1)}}}{{\text{5}}^{\text{(3+1)}}}\]

         \[\text{= (-1}{{\text{)}}^{\text{2}}}{{\text{(5)}}^{\text{4}}}\]

\[\Rightarrow {{\text{a}}_{\text{3}}}\text{= 625}\]

For $\text{n = 4}$

      \[{{\text{a}}_{\text{4}}}\text{=  (-1}{{\text{)}}^{\text{(4-1)}}}{{\text{5}}^{\text{(4+1)}}}\]

         \[\text{= (-1}{{\text{)}}^{\text{3}}}{{\text{(5)}}^{\text{5}}}\]

\[\Rightarrow {{\text{a}}_{\text{4}}}\text{= -3125}\]

For $\text{n = 5}$

     \[{{\text{a}}_{\text{5}}}\text{= (-1}{{\text{)}}^{\text{(5-1)}}}{{\text{5}}^{\text{(5+1)}}}\]

         \[\text{= (-1}{{\text{)}}^{\text{4}}}{{\text{(5)}}^{\text{6}}}\]

\[\Rightarrow {{\text{a}}_{\text{5}}}\text{= 15625}\]

Hence the required first five terms of given sequence are  $\text{25,-125,625,-3125,15625}\text{.}$

6. Write the first five terms of the sequences whose ${{\text{n}}^{\text{th}}}$ term is \[{{\text{a}}_{\text{n}}}\text{= n}\frac{{{\text{n}}^{\text{2}}}\text{+5}}{\text{4}}\]. 

Ans:

First we will use the given sequence to find the required terms by putting $\text{n = 1,2,3,4,5}\text{.}$ 

Here we have 

For $\text{n = 1}$

     \[{{\text{a}}_{\text{1}}}\text{= 1 }\!\!\times\!\!\text{ }\frac{{{\text{1}}^{\text{2}}}\text{+5}}{\text{4}}\] 

        \[\text{= }\frac{\text{6}}{\text{4}}\]

\[\Rightarrow {{\text{a}}_{\text{1}}}\text{= }\frac{\text{3}}{\text{2}}\]

For  $\text{n = 2}$

     \[{{\text{a}}_{\text{2}}}\text{= 2 }\!\!\times\!\!\text{ }\frac{{{\text{2}}^{\text{2}}}\text{+5}}{\text{4}}\]

          \[\text{= 2 }\!\!\times\!\!\text{ }\frac{\text{9}}{\text{4}}\]

\[\Rightarrow {{\text{a}}_{\text{2}}}\text{= }\frac{\text{9}}{\text{2}}\]

For $\text{n = 3}$

     \[{{\text{a}}_{\text{3}}}\text{= 3 }\!\!\times\!\!\text{ }\frac{{{\text{3}}^{\text{2}}}\text{+5}}{\text{4}}\]

         \[\text{= 3 }\!\!\times\!\!\text{ }\frac{14}{\text{4}}\]

\[\Rightarrow {{\text{a}}_{\text{3}}}\text{= }\frac{\text{21}}{\text{2}}\]

For  $\text{n = 4}$

      \[{{\text{a}}_{\text{4}}}\text{=  4 }\!\!\times\!\!\text{ }\frac{{{\text{4}}^{\text{2}}}\text{+5}}{\text{4}}\]

\[\Rightarrow {{\text{a}}_{\text{4}}}\text{= 21}\]

For $\text{n = 5}$

      \[{{\text{a}}_{\text{5}}}\text{= 5 }\!\!\times\!\!\text{ }\frac{{{\text{5}}^{\text{2}}}\text{+5}}{\text{4}}\]

         \[\text{= 5 }\!\!\times\!\!\text{ }\frac{\text{30}}{\text{4}}\]

\[\Rightarrow {{\text{a}}_{\text{5}}}\text{= }\frac{\text{75}}{\text{2}}\]

Hence the required first five terms of given sequence are  $\frac{\text{3}}{\text{2}}\text{,}\frac{\text{9}}{\text{2}}\text{,}\frac{\text{21}}{\text{2}}\text{,21,}\frac{\text{75}}{\text{2}}\text{.}$

7. Find the $\text{1}{{\text{7}}^{\text{th}}}$ and $\text{1}{{\text{8}}^{\text{th}}}$ term in the following sequence whose ${{\text{n}}^{\text{th}}}$ term is ${{\text{a}}_{\text{n}}}\text{=4n-3}$

Ans:

To find $\text{1}{{\text{7}}^{\text{th}}}$  term we will substitute $\text{n}$ by $\text{n =17}$

Here we have 

      ${{\text{a}}_{\text{17}}}\text{= 4(17)-3}$

      ${{\text{a}}_{\text{17}}}\text{=65-3}$

$\Rightarrow {{\text{a}}_{\text{17}}}\text{= 65}$

To find ${{18}^{th}}$  term we will substitute $\text{n}$ by $\text{n =18}$

Here we have 

      ${{\text{a}}_{\text{24}}}\text{= 4(24)-3}$

      ${{\text{a}}_{\text{24}}}\text{= 96-3}$

$\Rightarrow {{\text{a}}_{\text{24}}}\text{= 93}$

Therefore the required $\text{1}{{\text{7}}^{\text{th}}}$ and ${{18}^{th}}$ terms are $\text{65}$  and $\text{93}$ respectively.

8. Find the ${{\text{7}}^{\text{th}}}$ term in the following sequence whose ${{\text{n}}^{\text{th}}}$ term is ${{\text{a}}_{\text{n}}}\text{=}\frac{{{\text{n}}^{\text{2}}}}{{{\text{2}}^{\text{n}}}}$

Ans:

To find ${{\text{7}}^{\text{th}}}$  term we will substitute $\text{n}$ by $\text{n = 7}$

Here we have 

       ${{\text{a}}_{\text{7}}}\text{=}\frac{{{\text{7}}^{\text{2}}}}{{{\text{2}}^{\text{7}}}}$

      ${{\text{a}}_{\text{7}}}\text{=}\frac{\text{49}}{\text{128}}$

$\Rightarrow {{\text{a}}_{\text{7}}}\text{=}\frac{\text{49}}{\text{128}}$

Therefore the required \[{{\text{7}}^{\text{th}}}\] term ${{\text{a}}_{\text{7}}}\text{=}\frac{\text{49}}{\text{128}}$

9. Find the ${{\text{9}}^{\text{th}}}$ term in the following sequence whose ${{\text{n}}^{\text{th}}}$ term is ${{\text{a}}_{\text{n}}}\text{=(-1}{{\text{)}}^{\text{n-1}}}{{\text{n}}^{\text{3}}}$

Ans:

To find ${{\text{9}}^{\text{th}}}$  term we will substitute $\text{n}$ by $\text{n = 9}$

Here we have 

       \[{{\text{a}}_{\text{9}}}\text{= (-1}{{\text{)}}^{\text{9-1}}}{{\text{(9)}}^{\text{3}}}\]

      ${{\text{a}}_{\text{9}}}\text{=(-1}{{\text{)}}^{\text{8}}}\text{ }\!\!\times\!\!\text{ 729}$

$\Rightarrow {{\text{a}}_{\text{9}}}\text{=729}$

Therefore the required ${{\text{9}}^{\text{th}}}$ term ${{\text{a}}_{\text{9}}}\text{=729}$

10. Find the $\text{2}{{\text{0}}^{\text{th}}}$ term in the following sequence whose ${{\text{n}}^{\text{th}}}$ term is ${{\text{a}}_{\text{n}}}\text{= }\frac{\text{n(n-2)}}{\text{n+3}}$

Ans:

To find $\text{2}{{\text{0}}^{\text{th}}}$  term we will substitute $\text{n}$ by $\text{n = 20}$

Here we have 

       \[{{\text{a}}_{\text{20}}}\text{ = }\frac{\text{20(20-2)}}{\text{20+3}}\]

      ${{\text{a}}_{\text{20}}}\text{ = }\frac{\text{20 }\!\!\times\!\!\text{ 18}}{\text{23}}$

$\Rightarrow {{\text{a}}_{\text{20}}}\text{ = }\frac{\text{360}}{\text{23}}$

Therefore the required $\text{2}{{\text{0}}^{\text{th}}}$ term ${{\text{a}}_{\text{20}}}\text{ = }\frac{\text{360}}{\text{23}}$

11. Find Write the first five terms of the following sequence and obtain the corresponding series: ${{\text{a}}_{\text{1}}}\text{= 3,}$ ${{\text{a}}_{\text{n}}}\text{=3}{{\text{a}}_{\text{n-1}}}\text{+2}$  for all $\text{n  1}$ 

Ans:

To find first five terms of given sequence we will use given values

Here we have 

${{\text{a}}_{\text{1}}}\text{= 3}$ 

Now substituting $\text{n = 2}$ in given sequence we have

     ${{\text{a}}_{2}}\text{=3}{{\text{a}}_{\text{2-1}}}\text{+2}$

$\Rightarrow {{\text{a}}_{\text{2}}}\text{= 3}{{\text{a}}_{\text{1}}}\text{+2}$

$\Rightarrow {{\text{a}}_{\text{2}}}\text{= 3(3)+2}$

$\Rightarrow {{\text{a}}_{\text{2}}}\text{= 11}$

Now substituting $\text{n = 3}$ in given sequence we have

     ${{\text{a}}_{\text{3}}}\text{=3}{{\text{a}}_{\text{3-1}}}\text{+2}$

$\Rightarrow {{\text{a}}_{\text{3}}}\text{= 3}{{\text{a}}_{\text{2}}}\text{+2}$

$\Rightarrow {{\text{a}}_{\text{3}}}\text{= 3(11)+2}$

$\Rightarrow {{\text{a}}_{\text{3}}}\text{= 35}$

Similarly 

     ${{\text{a}}_{4}}\text{= 3}{{\text{a}}_{3}}\text{+2}$

$\Rightarrow {{\text{a}}_{\text{4}}}\text{= 3(35)+2}$

$\Rightarrow {{\text{a}}_{\text{4}}}\text{= 107}$

And 

     ${{\text{a}}_{\text{5}}}\text{= 3}{{\text{a}}_{\text{4}}}\text{+2}$

$\Rightarrow {{\text{a}}_{\text{5}}}\text{= 3(107)+2}$

$\Rightarrow {{\text{a}}_{\text{5}}}\text{= 323}$

Therefore the first five terms of the sequence are $\text{3,11,35,107,323}\text{.}$ 

And the corresponding series is $\text{3+11+35+107+323+}......$

12. Find Write the first five terms of the following sequence and obtain the corresponding series: ${{\text{a}}_{\text{1}}}\text{= -1,}$ ${{\text{a}}_{\text{n}}}\text{=}\frac{{{\text{a}}_{\text{n-1}}}}{\text{n}}$  for all $\text{n}\ge \text{2}$ 

Ans:

To find first five terms of given sequence we will use given values

Here we have 

${{\text{a}}_{\text{1}}}\text{= -1}$ 

Now substituting $\text{n = 2}$ in given sequence we have

     ${{\text{a}}_{\text{2}}}\text{=}\frac{{{\text{a}}_{\text{2-1}}}}{\text{2}}$

$\Rightarrow {{\text{a}}_{\text{2}}}\text{=}\frac{{{\text{a}}_{\text{1}}}}{\text{2}}$

$\Rightarrow {{\text{a}}_{\text{2}}}\text{= -}\frac{\text{1}}{\text{2}}$

Now substituting $\text{n = 3}$ in given sequence we have

     ${{\text{a}}_{\text{3}}}\text{=}\frac{{{\text{a}}_{\text{3-1}}}}{\text{3}}$

\[\Rightarrow {{\text{a}}_{\text{3}}}\text{=}\frac{{{\text{a}}_{\text{2}}}}{\text{3}}\]

$\Rightarrow {{\text{a}}_{\text{3}}}\text{=}\frac{\left( \text{-}\tfrac{\text{1}}{\text{2}} \right)}{\text{3}}$

$\Rightarrow {{\text{a}}_{\text{3}}}\text{= -}\frac{\text{1}}{\text{6}}$

Similarly 

     ${{\text{a}}_{\text{4}}}\text{=}\frac{{{\text{a}}_{\text{4-1}}}}{\text{4}}$

\[\Rightarrow {{\text{a}}_{\text{4}}}\text{=}\frac{{{\text{a}}_{\text{3}}}}{\text{4}}\]

$\Rightarrow {{\text{a}}_{\text{4}}}\text{=}\frac{\left( \text{-}\tfrac{\text{1}}{\text{6}} \right)}{\text{4}}$

$\Rightarrow {{\text{a}}_{\text{4}}}\text{= -}\frac{\text{1}}{\text{24}}$

And 

     ${{\text{a}}_{\text{5}}}\text{=}\frac{{{\text{a}}_{\text{5-1}}}}{\text{5}}$

\[\Rightarrow {{\text{a}}_{\text{5}}}\text{=}\frac{{{\text{a}}_{\text{4}}}}{\text{5}}\]

$\Rightarrow {{\text{a}}_{\text{5}}}\text{=}\frac{\left( \text{-}\tfrac{\text{1}}{\text{24}} \right)}{\text{5}}$

$\Rightarrow {{\text{a}}_{\text{5}}}\text{= -}\frac{\text{1}}{\text{120}}$

Therefore the first five terms of the sequence are $\text{-1,-}\frac{\text{1}}{\text{2}}\text{,-}\frac{\text{1}}{\text{6}}\text{,-}\frac{\text{1}}{\text{24}}\text{,-}\frac{\text{1}}{\text{120}}\text{.}$ 

And the corresponding series is $\left( \text{-1} \right)\text{+}\left( \text{-}\frac{\text{1}}{\text{2}} \right)\text{+}\left( \text{-}\frac{\text{1}}{\text{6}} \right)\text{+}\left( \text{-}\frac{\text{1}}{\text{24}} \right)\text{+}\left( \text{-}\frac{\text{1}}{\text{120}} \right)\text{+}......$

13. Find Write the first five terms of the following sequence and obtain the corresponding series: ${{\text{a}}_{\text{1}}}\text{= }{{\text{a}}_{\text{2}}}\text{= 2,}$ ${{\text{a}}_{\text{n}}}\text{= }{{\text{a}}_{\text{n-1}}}\text{-1}$  for all $\text{n  2}$ 

Ans:

To find first five terms of given sequence we will use given values

Here we have 

${{\text{a}}_{\text{1}}}\text{= 2}$ 

${{\text{a}}_{\text{2}}}\text{= 2}$

Now substituting $\text{n = 3}$ in given sequence we have

     ${{\text{a}}_{\text{3}}}\text{=}{{\text{a}}_{\text{3-1}}}\text{-1}$

$\Rightarrow {{\text{a}}_{\text{3}}}\text{= }{{\text{a}}_{\text{2}}}\text{-1}$

\[\Rightarrow {{\text{a}}_{\text{3}}}\text{= 2-1}\]

$\Rightarrow {{\text{a}}_{\text{3}}}\text{= 1}$

Similarly 

     ${{\text{a}}_{\text{4}}}\text{= }{{\text{a}}_{\text{3}}}\text{-1}$

$\Rightarrow {{\text{a}}_{\text{4}}}\text{= 1-1}$

$\Rightarrow {{\text{a}}_{\text{4}}}\text{= 0}$

And 

     ${{\text{a}}_{\text{5}}}\text{= }{{\text{a}}_{\text{4}}}\text{-1}$

$\Rightarrow {{\text{a}}_{\text{5}}}\text{= 0-1}$

$\Rightarrow {{\text{a}}_{\text{5}}}\text{= -1}$

Therefore the first five terms of the sequence are $\text{2,2,1,0,-1}\text{.}$ 

And the corresponding series is $\text{2 + 2 + 1 + 0 + (-1) + }\text{. }\text{. }\text{.}$

14. The Fibonacci sequence is defined by ${{\text{a}}_{\text{1}}}\text{= }{{\text{a}}_{\text{2}}}\text{= 1}$ and c $\text{n  2}$  

Find $\frac{{{\text{a}}_{\text{n+1}}}}{{{\text{a}}_{\text{n}}}}\text{,}$ for $\text{n=1,2,3,4,5}\text{.}$ 

Ans:

To find the required sequence first we will find the first six terms of given sequence 

Here we have 

${{\text{a}}_{\text{1}}}\text{= 2}$ 

${{\text{a}}_{\text{2}}}\text{= 2}$

Now     ${{\text{a}}_{\text{3}}}\text{=}{{\text{a}}_{\text{2}}}\text{+}{{\text{a}}_{\text{1}}}$ 

$\Rightarrow {{\text{a}}_{\text{3}}}\text{=1+1}$ 

$\Rightarrow {{\text{a}}_{\text{3}}}\text{=2}$

Similarly 

$\Rightarrow {{\text{a}}_{\text{4}}}\text{=2+1}$

$\Rightarrow {{\text{a}}_{\text{4}}}\text{=3}$

And 

$\Rightarrow {{\text{a}}_{\text{5}}}\text{= 3+2}$

$\Rightarrow {{\text{a}}_{\text{5}}}\text{=5}$

And 

$\Rightarrow {{\text{a}}_{\text{6}}}\text{= 5+3}$

\[\Rightarrow {{\text{a}}_{\text{6}}}\text{= 8}\]

Now $\frac{{{\text{a}}_{\text{n+1}}}}{{{\text{a}}_{\text{n}}}}\text{,}$

For $\text{n=1}$ 

$\frac{{{\text{a}}_{\text{2}}}}{{{\text{a}}_{\text{1}}}}\text{=}\frac{\text{1}}{\text{1}}$

$\Rightarrow \frac{{{\text{a}}_{\text{2}}}}{{{\text{a}}_{\text{1}}}}\text{=1}$

For $\text{n=2}$

$\frac{{{\text{a}}_{\text{3}}}}{{{\text{a}}_{\text{2}}}}\text{=}\frac{\text{2}}{\text{1}}$

$\Rightarrow \frac{{{\text{a}}_{\text{3}}}}{{{\text{a}}_{\text{2}}}}\text{=2}$

For $\text{n=3}$

$\frac{{{\text{a}}_{\text{4}}}}{{{\text{a}}_{\text{3}}}}\text{=}\frac{\text{3}}{\text{2}}$

For $\text{n=4}$

$\frac{{{\text{a}}_{\text{5}}}}{{{\text{a}}_{\text{4}}}}\text{=}\frac{\text{5}}{\text{3}}$

For $\text{n=5}$

$\frac{{{\text{a}}_{\text{6}}}}{{{\text{a}}_{\text{5}}}}\text{=}\frac{\text{8}}{\text{5}}$

Hence required $\frac{{{\text{a}}_{\text{n+1}}}}{{{\text{a}}_{\text{n}}}}\text{,}$for \[\text{n=1,2,3,4,5}\text{.}\]are $\text{1,2,}\frac{\text{3}}{\text{2}}\text{,}\frac{\text{5}}{\text{3}}\text{,}\frac{\text{8}}{\text{5}}\text{.}$

NCERT Solutions For Class 11 Maths Chapter 9 Sequences And Series Exercise 9.1

Opting for the NCERT solutions for Ex 9.1 Class 11 Maths is considered as the best option for the CBSE students when it comes to exam preparation. This chapter consists of many exercises. Out of which we have provided the Exercise 9.1 Class 11 Maths NCERT solutions on this page in PDF format. You can download this solution as per your convenience or you can study it directly from our website/ app online.

Vedantu in-house subject matter experts have solved the problems/ questions from the exercise with the utmost care and by following all the guidelines by CBSE. Class 11 students who are thorough with all the concepts from the Maths textbook and quite well-versed with all the problems from the exercises given in it, then any student can easily score the highest possible marks in the final exam. With the help of this Class 11 Maths Chapter 9 Exercise 9.1 solutions, students can easily understand the pattern of questions that can be asked in the exam from this chapter and also learn the marks weightage of the chapter. So that they can prepare themselves accordingly for the final exam.

Besides these NCERT solutions for Class 11 Maths Chapter 9 Exercise 9.1, there are plenty of exercises in this chapter which contain innumerable questions as well. All these questions are solved/answered by our in-house subject experts as mentioned earlier. Hence all of these are bound to be of superior quality and anyone can refer to these during the time of exam preparation. In order to score the best possible marks in the class, it is really important to understand all the concepts of the textbooks and solve the problems from the exercises given next to it. 

Do not delay any more. Download the NCERT solutions for Class 11 Maths Chapter 9 Exercise 9.1 from Vedantu website now for better exam preparation. If you have the Vedantu app in your phone, you can download the same through the app as well. The best part of these solutions is these can be accessed both online and offline as well.