NCERT Solutions for Class 12 Physics Chapter 1

NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields

Vedantu.com - No.1 online tutoring company in India provides you Free PDF download of NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 1 - Electric Charges and Fields Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks. Register for online coaching for IIT JEE (Mains & Advanced), NEET, Engineering and Medical entrance exams.

NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields

NCERT Grade 12 Physics, Chapter 1, Electric Charges and Fields from Unit 1, Electrostatics deals with electricity, charge, discharge and generation of static electricity.What is electrostatics and its wider components are discussed in this chapter. 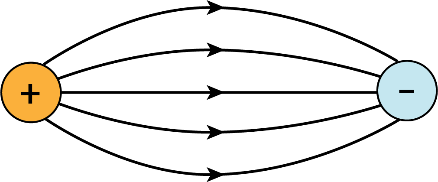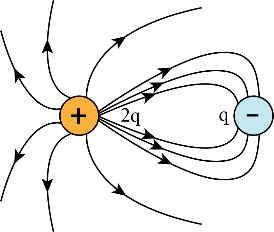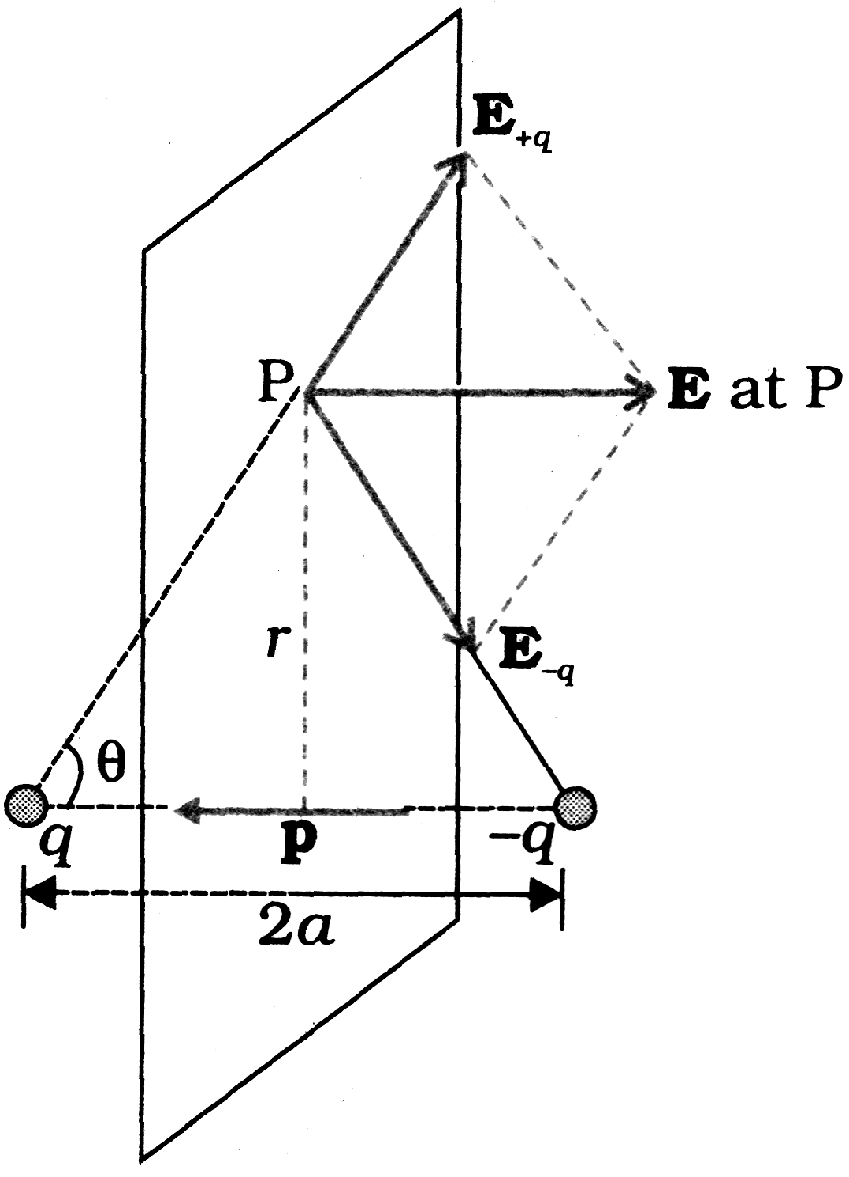Electric Charge, Conductors and Insulators, Charging by Induction, Basic Properties of Electric Charge, Additivity of charges, Charge is conserved, Quantisation of charge, Coulomb’s Law, Forces Between Multiple Charges, Electric Field, Electric field due to a system of charges, Physical significance of electric field, Electric Field Lines, Electric Flux, Electric Dipole, The field of an electric dipole, Physical significance of dipoles, Dipole in a Uniform External Field, Continuous Charge Distribution, Gauss’s Law, Applications of Gauss’s Law, Field due to an infinitely long straight uniformly charged wire, Field due to a uniformly charged infinite plane sheet and Field due to a uniformly charged thin spherical shell are the topics discussed in this chapter.

Diagrams, graphs, illustrations and examples associated to daily life make this chapter very interesting and easy to learn. Solved numeral problems and unsolved for practice make the students understand the concept better and develop a strong grip on the subject.NCERT Grade 12 Physics, Chapter 1, Electric Charges and Fields from Unit 1, Electrostatics. Unit 1 holds a total weightage of 8 marks in the final examination according to the latest pattern.

Get 100 percent accurate NCERT Solutions for Class 12 Physics Chapter 1 (Electric Charges and Fields) solved by expert Physics teachers. We provide solutions for questions given in Class 12 Physics text-book as per CBSE Board guidelines from the latest NCERT book for Class 12 Physics. The topics and sub-topics in Chapter 1 Electric Charges and Fields are given below.

Ex 1.1 - INTRODUCTION

Ex 1.2 - ELECTRIC CHARGE

Ex 1.3 - CONDUCTORS AND INSULATORS

Ex 1.4 - CHARGING BY INDUCTION

Ex 1.5 - BASIC PROPERTIES OF ELECTRIC CHARGE

Ex 1.5.1 - Additivity of charges

Ex 1.5.2 - Charge is conserved

Ex 1.5.3 - Quantisation of charge

Ex 1.6 - COULOMB’S LAW

Ex 1.7 - FORCES BETWEEN MULTIPLE CHARGES

Ex 1.8 - ELECTRIC FIELD

Ex 1.8.1 - Electric field due to a system of charges

Ex 1.8.2 - Physical significance of electric field

Ex 1.9 - ELECTRIC FIELD LINES

Ex 1.10 - ELECTRIC FLUX

Ex 1.11 - ELECTRIC DIPOLE

Ex 1.11.1 - The field of an electric dipole

Ex 1.11.2 - Physical significance of dipoles

Ex 1.12 - DIPOLE IN A UNIFORM EXTERNAL FIELD

Ex 1.13 - CONTINUOUS CHARGE DISTRIBUTION

Ex 1.14 - GAUSS’S LAW

Ex 1.15 - APPLICATIONS OF GAUSS’S LAW

Ex 1.15.1 - Field due to an infinitely long straight uniformly charged wire

Ex 1.15.2 - Field due to a uniformly charged infinite plane sheet

Ex 1.15.3 - Field due to a uniformly charged thin spherical shell.

We cover all exercises in the chapter given below:-

Chapter 1 Exercises - 34 Questions with Solutions.

Other than given exercises, you should also practice all the solved examples given in the book to clear your concepts on Electric Charges and Fields. Download the free PDF of Chapter 1 Electric Charges and Fields and take the print out to keep it handy for your exam preparation.