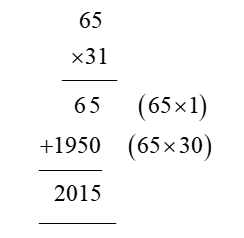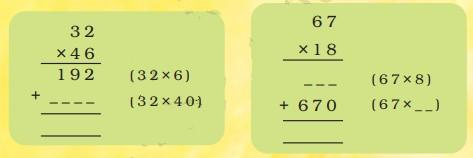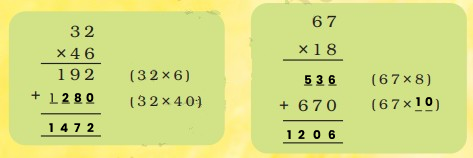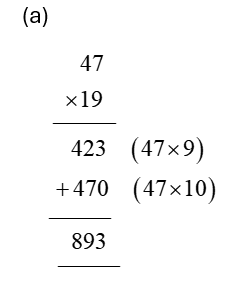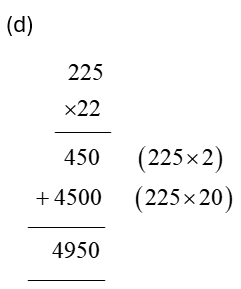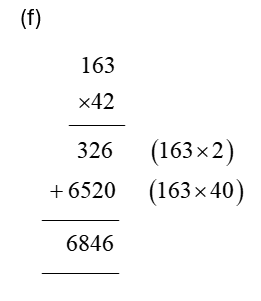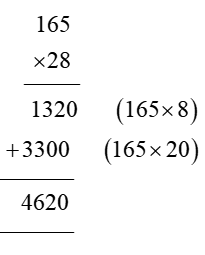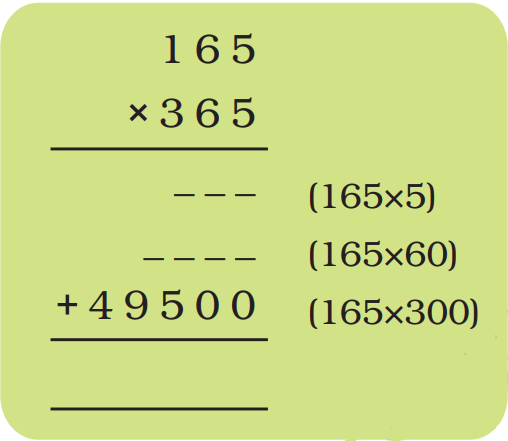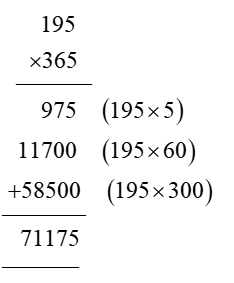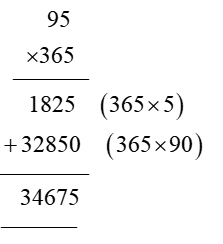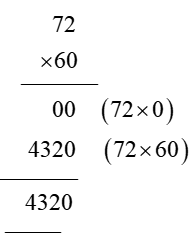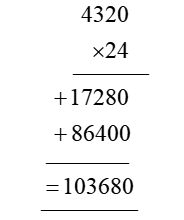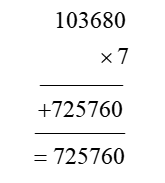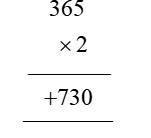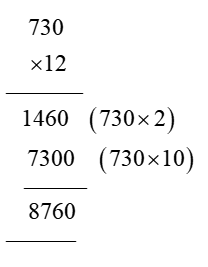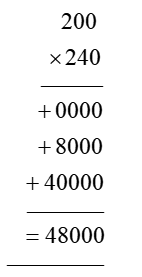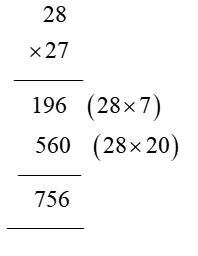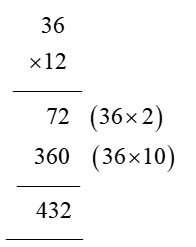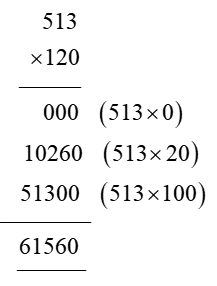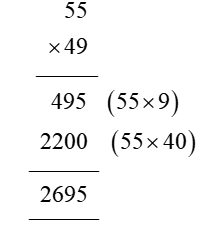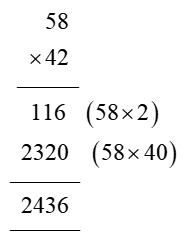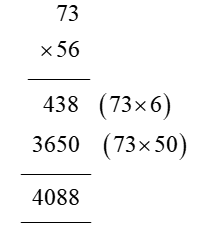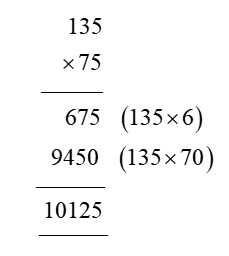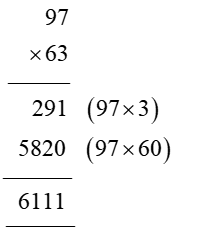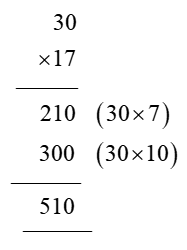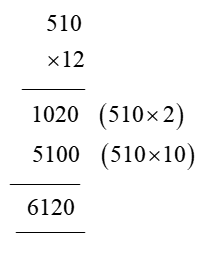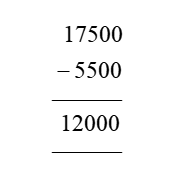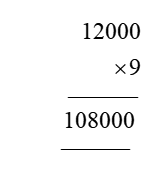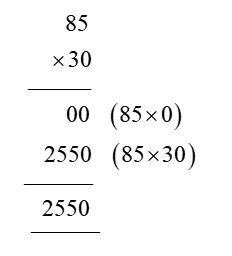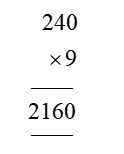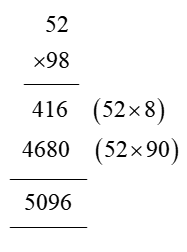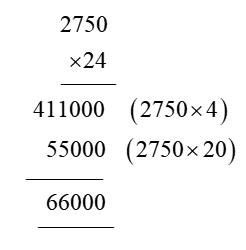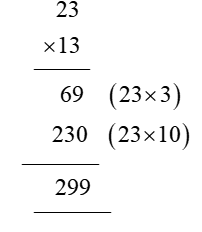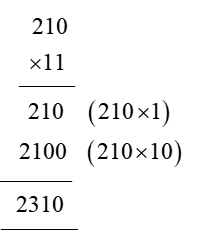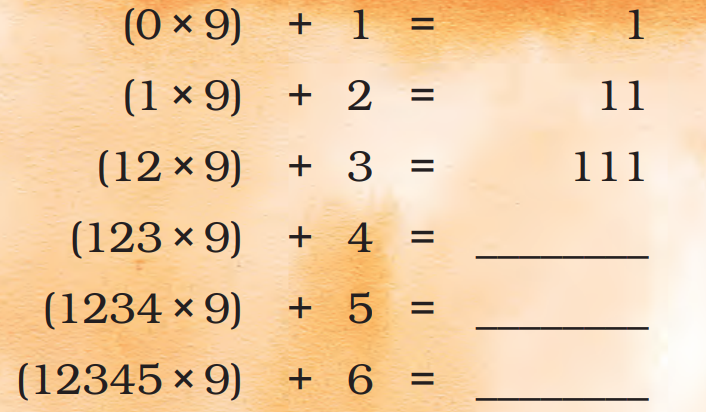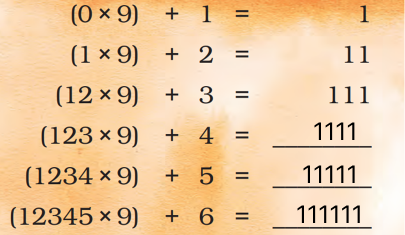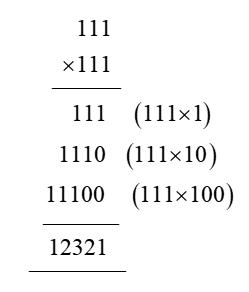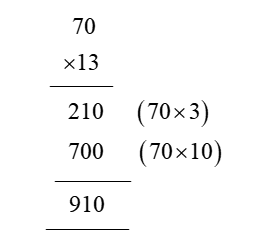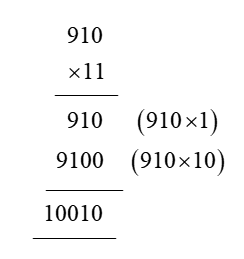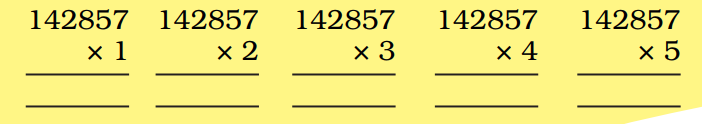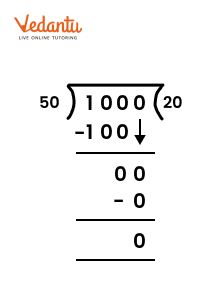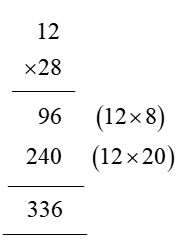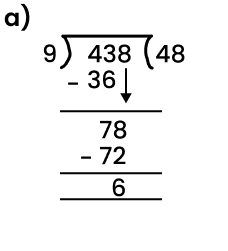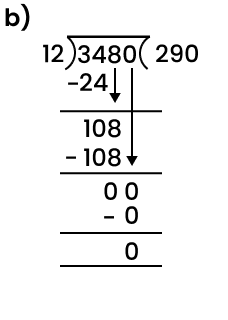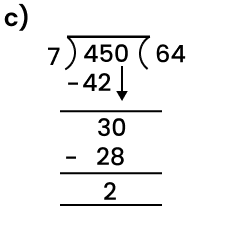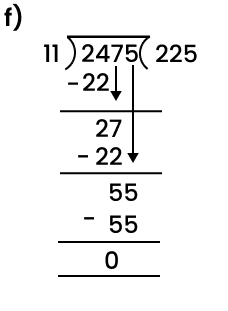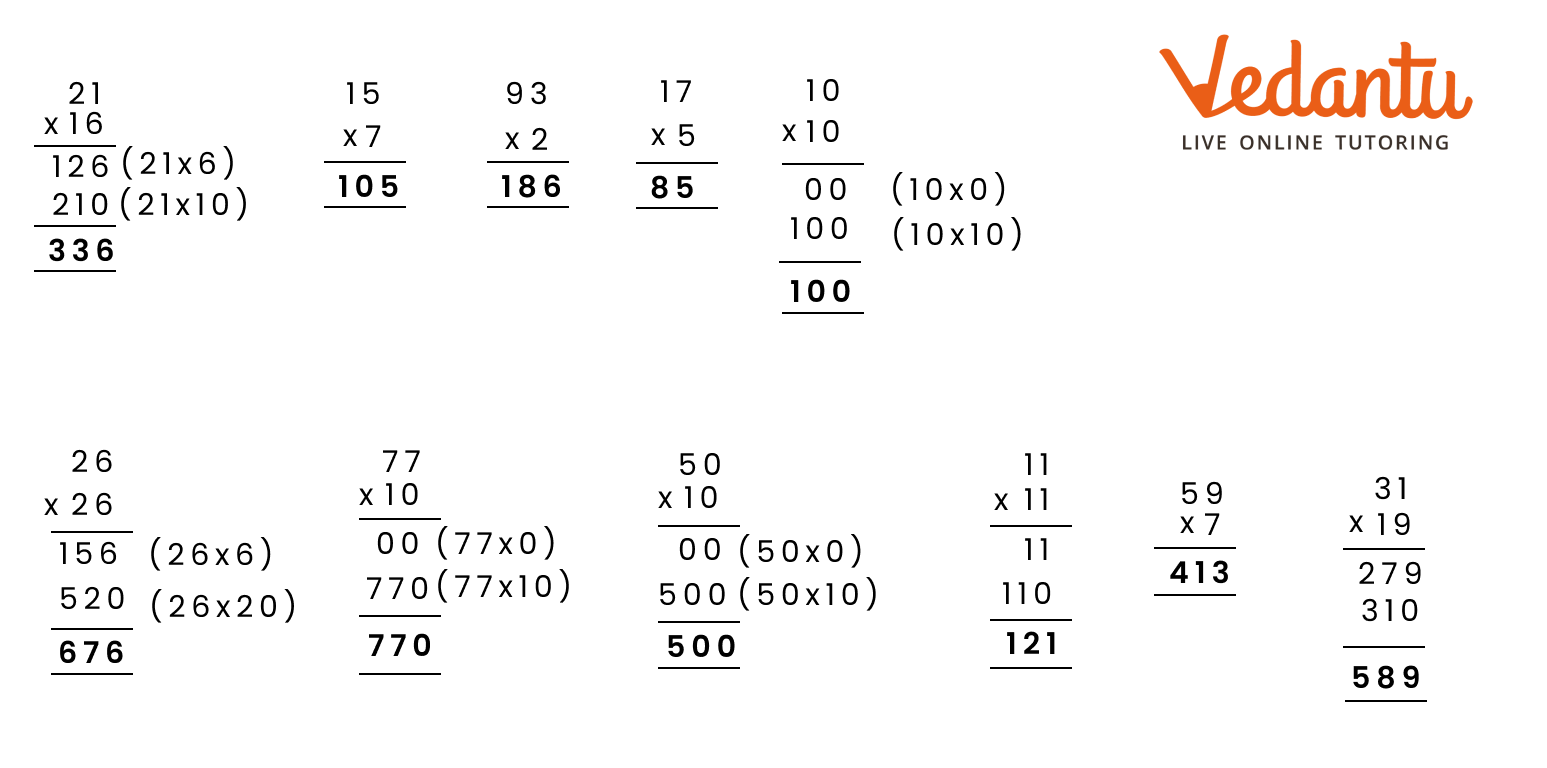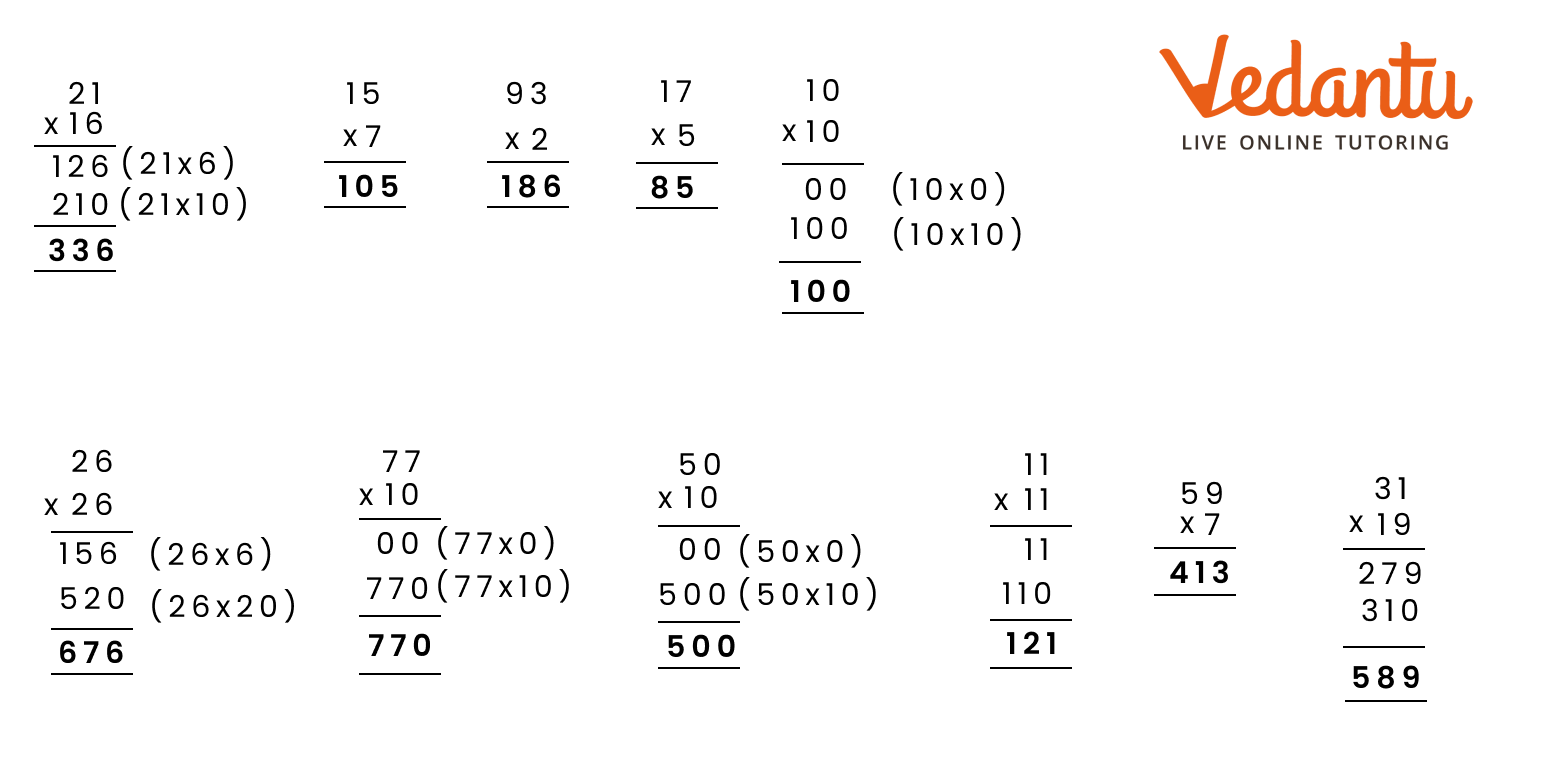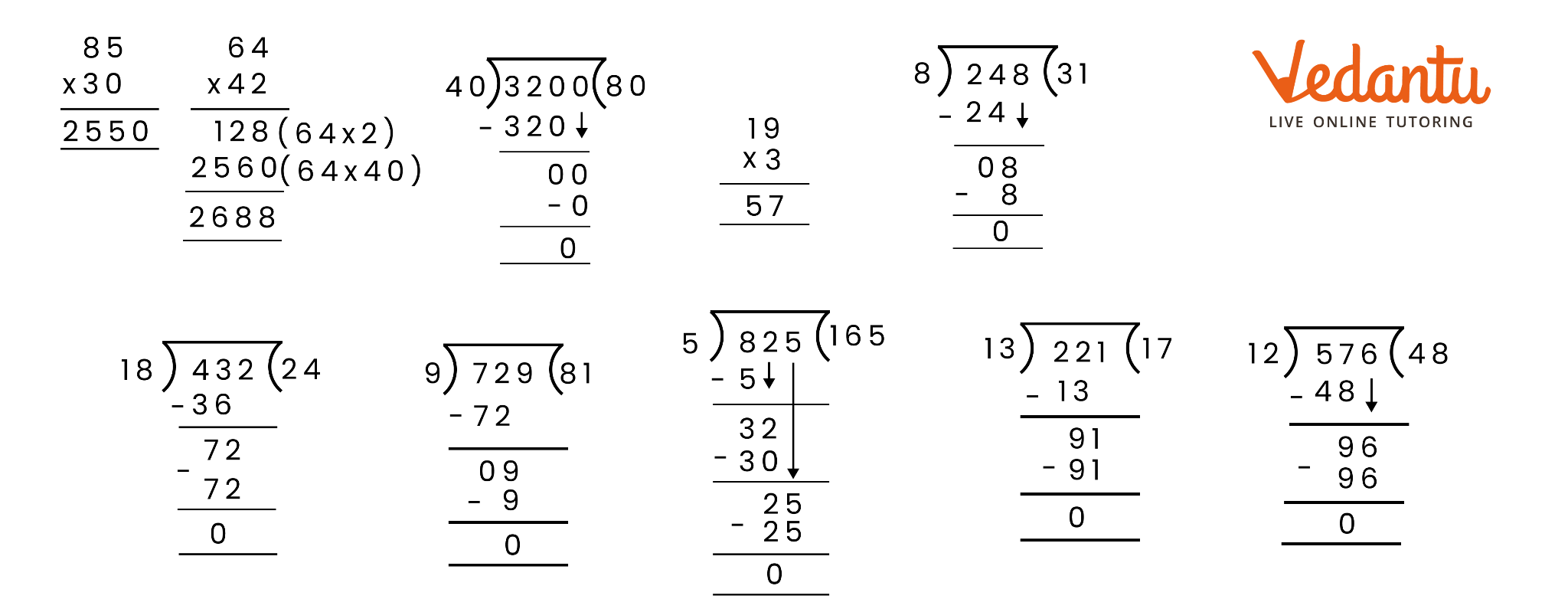NCERT Solutions for Class 5 Maths Ways to Multiply and Divide Chapter 13 - FREE PDF Download
FAQs on NCERT Solutions for Class 5 Maths Chapter 13 Ways To Multiply and Divide
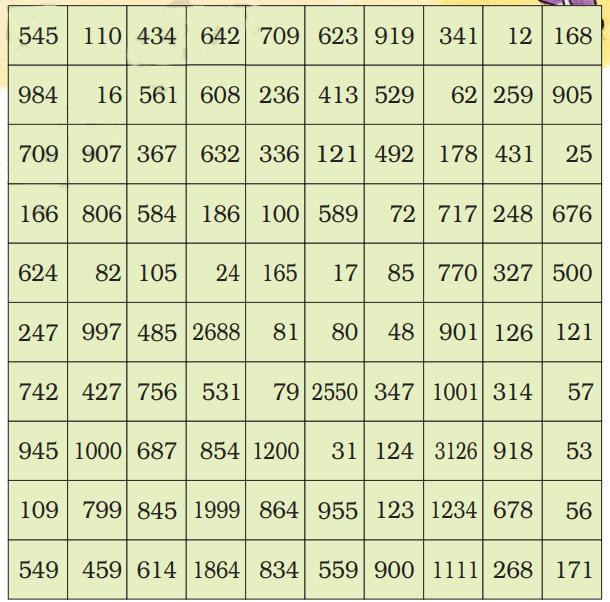
1. How to do column multiplication?
In order for students to use column multiplication to solve an equation, they are required to have a clear concept on multiplication. They will need to first develop an understanding of multiplying single digits with one another and then slowly proceed to multiply two digits with single digits. After practising these simple concepts, only then can students proceed with column multiplication.
For column multiplications in case of three digits or two digits numbers with two digits numerical, first, start with the 2nd or last digit of the number the student is multiplying to. Multiply this digit with the number on top of the column. Record the answer below, and under that put a cross in the unit section and record the answer derived from multiplying the tenth digit of the numerical to the number on top. Add the two answers to arrive at a solution.
2. How to solve equations using story format?
In NCERT, to intrigue, the logical thinking of a student, a story format or problem-solving equations may be included within this lesson plan. In such cases, students will need to understand the equation well before they proceed to derive a solution. In order for students to be apt at problem-solving equations, they require a clear concept on the subject.
With solutions from Vedantu, students are able to develop a proper conceptual understanding of the subject. They are able to solve their lesson plan much faster as the equations and examples provided here, tend to appear in examinations as well.
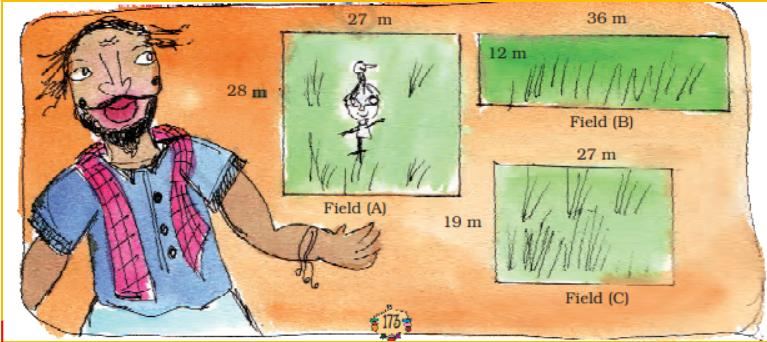
3. How to find an area square meter using multiplication?
Within this solution, students are required to solve an equation involving finding the area of a field using multiplication. In order to derive a solution, students are required to attain the length and breadth of the fields first. After deriving the length and breadth, they must multiply them to find the area of the field.
The process of deriving a solution for these kinds of problems is pretty easy as long as students have a clear conceptual idea in this chapter.
4. What is Chapter 13 of the Class 5th Maths textbook about?
The title of the chapter is Ways to Multiply and Divide. Multiplication and division are two of the most important elements of Mathematics, other than addition and subtraction, that we use almost daily in one way or the other. Multiplication and division make our calculation faster and easier. The chapter describes how in a variety of scenarios, multiplication, and division come in handy. The chapter provides a strong foundation for higher classes.
5. How difficult is the chapter ‘Ways to Multiply and Divide’?
The chapter is as difficult as any other new concept appears to be. Anything that one is not aware of or familiar with, scares us. The same goes for Mathematics. The chapter helps you develop a basic understanding of how to multiply and divide. The chapter provides you with a number of examples of several types. The sole purpose of the chapter is to get you familiar with multiplication and division easily. The chapter is easy given you have a basic understanding and practice.
6. What is a remainder?
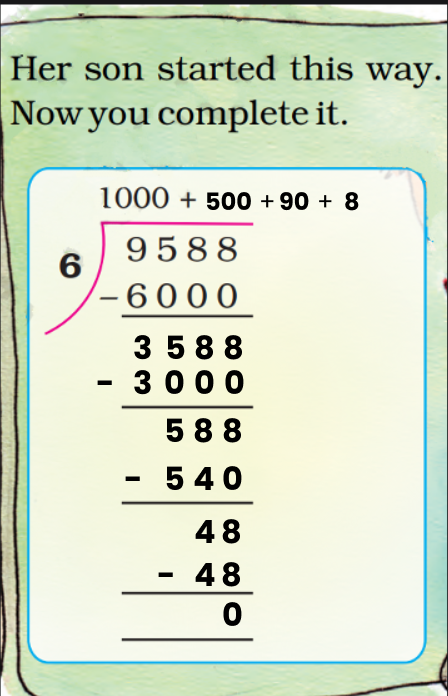
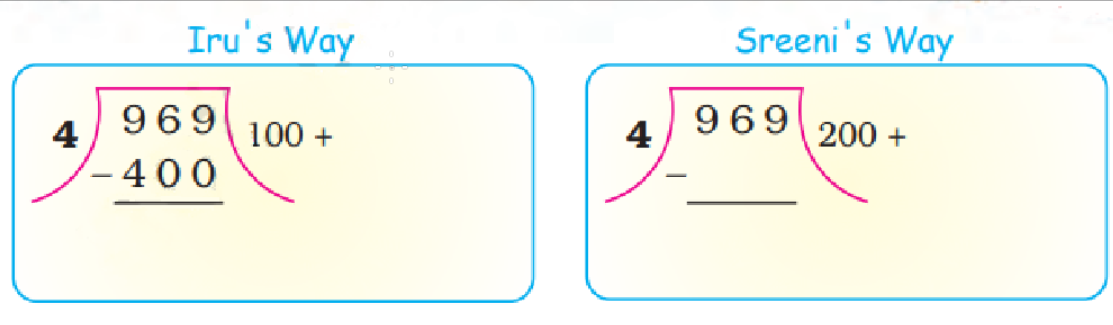
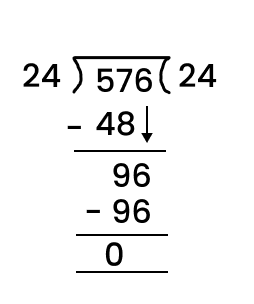
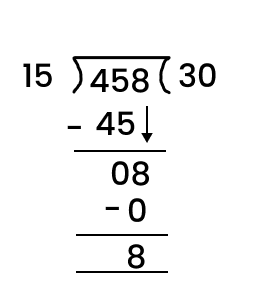
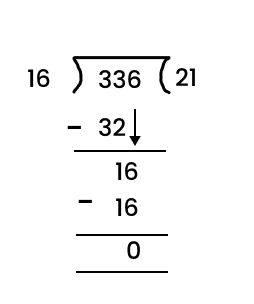
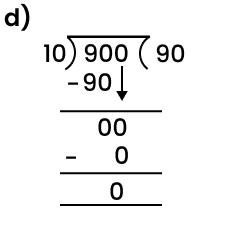
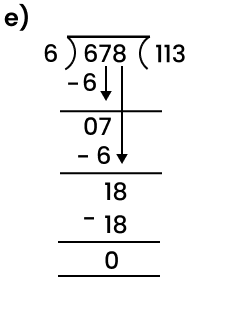
When you divide a number, say N, by a divisor A, the number N may not be entirely divisible by A. The remainder is the number we get after performing division that cannot be further divided by the divisor. If the remainder is zero the number is completely divisible by the divisor (the number we are trying to divide by). For example, let us try to divide 8 by 3. We know that 3*2 will give us 6 and 3*4 will give us 12. Since 3*2 will give us a number that is smaller and closest to 8 we will use it for division purposes. Now, we will get 2 (8-6=2). The number 2 is smaller than 3 implies that it cannot be further divided by 3, 2 is our remainder.
7. Can I do the chapter ‘Ways to Multiply and Divide’ on my own?
The chapter will help you develop a strong understanding of the two of the most important functions that we perform in arithmetic. The chapter contains several examples of different types that you can do on your own if your basics of mathematics and division are strong. The chapter is application-based. Keep a notebook and a pen when you are studying. For all the examples that you come across, attempt them yourself. You can take the help of Vedantu’s NCERT Solutions to understand a question or concept better.
8. Is Vedantu a good website for the chapter ‘Ways to Multiply and Divide’?
There are numerous websites that do provide good content and explanation for boosting your preparation. Vedantu is one of the few websites that will give your preparation and understanding of the concepts and edge over the others. The faculty at Vedantu put their heart and soul into preparing the content that can be easily accessed and understood. The explanation and the NCERT Solutions provided at Vedantu are prepared by the faculty after thorough research and are as per the revised curriculum.
9. What is the importance of learning multiplication and division for Class 5 maths chapter 13 PDF?
Multiplication and division are fundamental arithmetic operations essential for solving complex mathematical problems. They help in understanding advanced concepts, improving problem-solving skills, and are applicable in real-life situations such as budgeting and measuring.
10. How can parents help their children practice multiplication and division at home for ncert class 5 maths chapter 13 solutions?
Parents can help by creating engaging activities such as multiplication games, flashcards, and daily practice worksheets. They can also incorporate practical examples like cooking measurements or shopping calculations to make learning fun and relevant.
11. What strategies can students use to master multiplication and division in class 5 math chapter 13?
Students can use strategies like repeated addition for multiplication, skip counting, and breaking down larger numbers into smaller, manageable parts. For division, understanding remainders and using division facts (similar to multiplication tables) can be very effective.
12. What topics are covered in NCERT Solutions for Class 5 Maths Chapter 13?
The chapter covers various methods of multiplication and division, including different techniques and strategies to make these operations easier for students.
13. Are these NCERT solutions helpful for exam preparation?
Yes, the solutions are designed to help students understand the concepts thoroughly, practice problem-solving, and prepare effectively for their exams.
14. Can I download the NCERT Solutions for Class 5 Maths Chapter 13 in PDF format?
Yes, Vedantu offers the option to download the solutions in PDF format for offline study.
15. Do the solutions of class 5 chapter 13 include step-by-step explanations?
Yes, the solutions provide detailed, step-by-step explanations for each problem, helping students grasp the concepts better.