NCERT Solutions for Class 6 Maths Exercise 1.2 Chapter 1 Patterns in Mathematics - FREE PDF Download
NCERT Solutions for Class 6 Maths Chapter 1, Exercise 1.2, "Patterns in Numbers," are designed to help students understand and practice number patterns effectively. These solutions align with the CBSE Class 6 Maths Syllabus, offering clear explanations and step-by-step guidance to help students grasp the basics of identifying and working with number patterns.
You can download these NCERT Solutions for Maths Class 6 as a FREE PDF, making it easy for students to enhance their problem-solving skills and prepare for exams. The solutions include helpful tips and shortcuts to make learning engaging and effective. With these resources, students can practise number patterns and improve a strong foundation for tackling more advanced mathematical topics.
Glance on NCERT Solutions Maths Chapter 1 Exercise 1.2 Class 6 | Vedantu
This exercise focuses on understanding and identifying patterns in numbers.
This exercise introduces students to various types of number patterns, such as sequences and series, and teaches them how to recognize and extend these patterns.
By working through the problems, students learn to find regularities and predict the next numbers in a sequence.
These solutions provide clear explanations and step-by-step guidance to help students grasp these concepts and apply them effectively.
Table 1: Examples of number sequences
1. Can you recognise the pattern in each of the sequences in Table 1?
Ans: (a) 1, 1, 1, 1, 1, 1, 1, ……
The number ‘1’ is repeated indefinitely.
(b) 1, 2, 3, 4, 5, 6, 7, ……
Counting numbers starting from ‘1’. Each number increases by 1.
(c) 1, 3, 5, 7, 9, 11, 13, ……
Odd numbers. Start from 1 and keep adding 2.
(d) 2, 4, 6, 8, 10, 12, 14, ……
Even numbers. Start from 2 and keep adding 2.
(e) 1, 3, 6, 10, 15, 21, 28, ……
Triangular numbers. Each term is the sum of the natural numbers up to that term.
(f) 1, 4, 9, 16, 25, 36, 49, ……
Square numbers. Each term is the square of its position ($1^{2}$, $2^{2}$, $3^{2}$, ...).
(g) 1, 8, 27, 64, 125, 216, ……
Cube numbers. Each term is the cube of its position (($1^{2}$, $2^{2}$, $3^{2}$, ...).
(h) 1, 2, 3, 5, 8, 13, 21, ……
Virahānka numbers (Fibonacci sequence). Each number is the sum of the two preceding numbers.
(i) 1, 2, 4, 8, 16, 32, 64, ……
Powers of 2. Each term is raised to the power of its position ($2^{0}$, $2^{1}$, $2^{2}$, ...).
(j) 1, 3, 9, 27, 81, 243, 729, ……
Powers of 3. Each term is 3 raised to the power of its position ($3^{0}$, $3^{1}$, $3^{2}$, ...).
2. Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.
Ans:
(a) 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
The sequence consists of repeating the number 1. The next three numbers are also 1.
(b) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
This is a sequence of consecutive counting numbers. The next three numbers are 8, 9, and 10.
(c) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, …
These are consecutive odd numbers, increasing by 2. The next three numbers are 15, 17, and 19.
(d) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …
The sequence contains even numbers, increasing by 2. The next three numbers are 16, 18, and 20.
(e) 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …
A sequence of triangular numbers where each number is the sum of the natural numbers up to a certain point.
28 + 8 = 36
36 + 9 = 45
45 + 10 = 55
(f) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …
Square numbers are formed by multiplying a number by itself. The next three are 64, 81, and 100.
$8^{2}$ = 64
$9^{2}$ = 81
$10^{2}$ = 100
(g) 1, 8, 27, 64, 125, 216, 343, 512, 729, …
A sequence of cube numbers where each number is the cube of a natural number. The next three numbers are 343, 512, and 729.
$7^{3}$ = 343
$8^{3}$ = 512
$9^{3}$ = 729
(h) 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
This is the Fibonacci (Virahanka) sequence, where each number is the sum of the previous two. The next three numbers are 34, 55, and 89.
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
(i) 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, …
This shows powers of 2, where each number is multiplied by 2. The next three numbers are 128, 256, and 512.
64 × 2 = 128
128 × 2 = 256
256 × 2 = 512
(j) 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, …
This shows powers of 3, where each number is multiplied by 3. The next three numbers are 2187, 6561, and 19683.
729 × 3 = 2187
2187 × 3 = 6561
6561 × 3 = 19683
Benefits of NCERT Solutions for Class 6 Maths Chapter 1 Exercise 1.2 Patterns in Mathematics
This exercise helps students understand different numerical patterns better.
It improves their ability to identify and solve problems based on patterns.
By providing a basic understanding of algebraic relationships, it sets the stage for future algebra lessons.
The interesting nature of patterns makes learning more enjoyable and sparks curiosity.
It helps develop logical and clear thinking skills.
Learning about patterns prepares students for more advanced topics in later grades.
Recognising patterns connects students to real-world examples and practical uses.
Class 6 Maths Chapter 1: Exercises Breakdown
Important Study Material Links for Class 6 Maths Chapter 1 - Patterns in Mathematics
Conclusion
NCERT Solutions for Class 6 Maths Chapter 1 Exercise 1.2, "Patterns in Numbers," helps students understand various numerical patterns with clear explanations. Practising these exercises improves their ability to recognize and use patterns, supporting their overall learning and problem-solving skills. These solutions make practice and learning easier, helping students feel more confident in their abilities. Available as a FREE PDF download, they provide a convenient way for students to study and review whenever they need.
Chapter-Specific NCERT Solutions for Class 6 Maths
The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Related Important Links for Maths Class 6
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.
FAQs on NCERT Solutions for Class 6 Maths Chapter 1 - Patterns in Mathematics Exercise 1.2
1. What is Exercise 1.2 in Chapter 1 about?
Exercise 1.2 focuses on "Patterns in Numbers," where students learn to identify and work with different numerical patterns. It includes tasks to help recognize sequences and understand how numbers change.
2. How can I use the NCERT Solutions for Exercise 1.2 effectively?
Use NCERT Solutions to practise spotting patterns and solving related problems. Follow the simple steps provided to understand each type of pattern and apply similar methods to new problems.
3. What types of patterns are covered in Exercise 1.2?
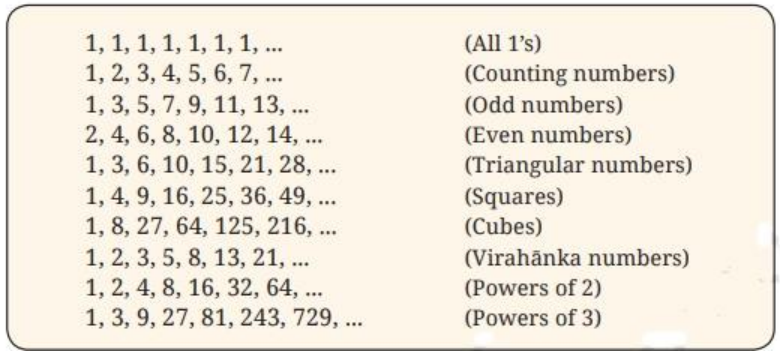
Exercise 1.2 covers different numerical patterns, including repeating patterns, counting numbers, odd and even numbers, and sequences like triangular and square numbers.
4. Why are patterns important in mathematics?
Patterns help in seeing regularities and relationships between numbers. Understanding patterns is essential for learning more advanced maths concepts and solving problems more easily.
5. Can NCERT Solutions help if I struggle with patterns?
Yes, the NCERT Solutions offer clear explanations and step-by-step answers that can help you understand patterns better. Practicing these solutions can make it easier to recognize and use patterns.
6. How do I approach solving problems in Exercise 1.2?
Start by figuring out the type of pattern in each problem. Use the examples in the solutions to guide you, and apply the same approach to solve similar problems in the exercise.
7. Are the NCERT Solutions for Exercise 1.2 available for FREE?
Yes, the NCERT Solutions for Exercise 1.2 are available as a FREE PDF download from Vedantu. You can access them anytime to practise and review.
8. How can patterns in numbers help in future maths topics?
Understanding patterns provides a foundation for more advanced topics. It helps with learning sequences, series, and algebraic concepts, making future maths topics easier to understand.
9. What should I do if I can't solve a problem from Exercise 1.2?
Review the NCERT Solutions to see the step-by-step approach used. If you're still stuck, try practising similar problems or ask for help from a teacher or classmate.
10. How often should I practise Exercise 1.2 problems?
Regular practice is important. Try to solve a few problems from Exercise 1.2 each day to get comfortable with different patterns and improve your skills.
11. Can I use the NCERT Solutions for Exercise 1.2 for revision?
Yes, the NCERT Solutions are great for revision. You can review the solutions to refresh your understanding of patterns and prepare for tests or exams.
12. Are there any tips for learning patterns effectively?
Focus on understanding how each pattern works. Practise regularly and use NCERT Solutions to see how different patterns are solved. This will help you recognise and apply patterns more easily.
13. How do patterns in numbers relate to real-life situations?
Patterns can be found in everyday life, such as in schedules, designs, and sequences. Learning about patterns in numbers helps in understanding these real-life patterns and solving practical problems.
