NCERT Solutions for Class 6 Maths Chapter 1 Patterns In Mathematics Ex 1.4

Exercise 1.4

1. Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, gives square numbers?

Ans: 

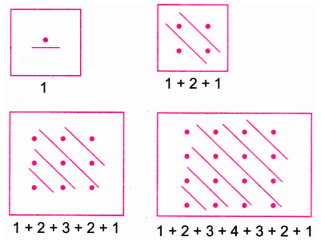
1. The first term is 1 (which is $1^{2}$).

2. The second term is 1 + 2 + 1 = 4 (which is $2^{2}$).

3. The third term is 1 + 2 + 3 + 2 + 1 = 9 (which is $3^{2}$).

Let's find the next three terms:

4. The fourth term is 1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 (which is $4^{2}$).

5. The fifth term is 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25 (which is $5^{2}$).

6. The sixth term is 1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36 (which is $6^{2}$).

2. By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be the value of 1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1? 

Ans: 

1. Understand the Pattern: The sequence starts with increasing numbers from 1 up to 100 and then decreases back to 1. It forms a symmetrical pattern around the number 100.

2. The sum of Increasing Sequence:
   $\text{Sum}_{1 \text{ to } 100} = \frac{100 \times (100 + 1)}{2} = \frac{100 \times 101}{2} = 5050$

3. The sum of Decreasing Sequence:
   $\text{Sum}_{1 \text{ to } 99} = \frac{99 \times (99 + 1)}{2} = \frac{99 \times 100}{2} = 4950$

4. Add the Two Sums:
   $\text{Total Sum} = 5050 + 100 + 4950 = 10000$

So, the value of 1 + 2 + 3 + ... + 99 + 100 + 99 + … + 3 + 2 + 1 is 10,000.

3. Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?

Ans: When adding up a sequence of 1’s, such as 1 + 1 + 1 + 1, the result is 4. 

Similarly, when adding down a sequence of 1’s, such as 1 + 1 + 1 + 1 the sum remains 4. This shows that whether you add the 1’s up or down, the total sum is the same in both cases.

4. Which sequence do you get when you start to add the counting numbers up? Can you give a smaller pictorial explanation?

Ans: 

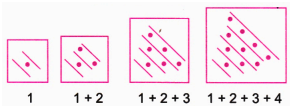
When you add up the counting numbers sequentially, you get the following sequence:

1. Start with 1.

2. Next, add 1 + 2 to get 3.

3. Then, add 1 + 2 + 3 to get 6.

4. Finally, add 1 + 2 + 3 + 4 to get 10.

5. What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, …? Which sequence do you get? Why? Can you explain it with a picture?

Ans: Identify the Triangular Numbers: Triangular numbers are: 1,3,6,10,15,…

Add the First Pair:
1 + 3 = 4
This is the first pentagonal number.

Add the Second Pair:
3 + 6 = 9
This is the second pentagonal number.

Add the Third Pair:
6 + 10 = 16
This is the third pentagonal number.

Add the Fourth Pair:
10 + 15 = 25
This is the fourth pentagonal number.

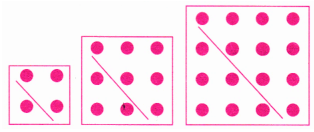
Each sum of consecutive triangular numbers forms a pentagonal number because the total number of dots creates a pentagon shape. This pattern reflects the arrangement of dots in a pentagonal figure.

6. What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, …? Now add 1 to each of these numbers—what numbers do you get? Why does this happen?

Ans: When you start adding up powers of 2, you get a sequence of numbers that are one less than the next power of 2. Here's a detailed explanation:

Adding Powers of 2:

1. Start with 1: 1

2. Add the next power of 2 (2): 1 + 2 = 3

3. Add the next power of 2 (4):1 + 2 + 4 = 7

4. Add the next power of 2 (8): 1 + 2 + 4 + 8 = 15

5. Add the next power of 2 (16): 1 + 2 + 4 + 8 + 16 = 31

Adding 1 to Each Number:

1. Add 1 to 1: 1 + 1 = 2

2. Add 1 to 3: 3 + 1 = 4

3. Add 1 to 7: 7 + 1 = 8

4. Add 1 to 15: 15 + 1 = 16

5. Add 1 to 31: 31 + 1 = 32

Explanation:

When you add up powers of 2, the sum is always one less than the next power of 2. This happens because:

• The sum of the first n powers of 2 is $2^{0}$ + $2^{1}$ + $2^{2}$ + ... + $2^{n-1}$.

• This sum can be simplified using the formula for a geometric series: $S_{n} = 2^{n} - 1$.

• Therefore, when you add 1 to this sum, you get $2^{n}$, which is the next power of 2.

So, the sequence you get after adding 1 to each of these sums is 2, 4, 8, 16, 32,…

This is the sequence of powers of 2.

7. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture? 

Ans: 

Triangular numbers follow the sequence: 1, 3, 6, 10, 15, 21, etc. When you multiply each triangular number by 6 and add 1, you get a new sequence:

• $1 \times 6 + 1 = 7$

• $3 \times 6 + 1 = 19$ (increase of 12)

• $6 \times 6 + 1 = 37$ (increase of 18)

• $10 \times 6 + 1 = 61$ (increase of 24)

• $15 \times 6 + 1 = 91$ (increase of 30)

Thus, the sequence becomes 7, 19, 37, 61, 91, and so on. This pattern shows that each term increases by 6 more than the previous increase.

8. What happens when you start to add up hexagonal numbers, i.e., take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, … ? Which sequence do you get? Can you explain it using a picture of a cube?

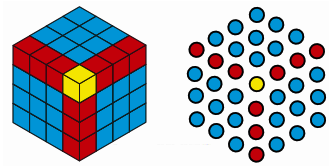
Ans: Hexagonal numbers follow the sequence: 1, 7, 19, 37, and so on. When you sum these numbers sequentially, you observe the following results:

• The sum of the first hexagonal number is 1, which equals $1^{3}$ (the cube of 1).

• Adding the second hexagonal number 7 gives 1 + 7 = 8, which is $2^{3}$ (the cube of 2).

• Adding the third hexagonal number 19 results in 1 + 7 + 19 = 27, which is 333^333 (the cube of 3).

• Adding the fourth hexagonal number 37 yields 1 + 7 + 19 + 37 = 64, which is $4^{3}$ (the cube of 4).

• Adding the fifth hexagonal number 616161 gives 1 + 7 + 19 + 37 + 61 = 125, which is $5^{3}$ (the cube of 5).

This pattern illustrates that the cumulative sum of the first n hexagonal numbers equals $n^{3}$, demonstrating an interesting relationship between hexagonal numbers and perfect cubes.

9. Find your own patterns or relations in and among the sequences in Table 1. Can you explain why they happen with a picture or otherwise?

Ans: Here are two simple patterns:

1. Multiples of 3: The sequence 3,6,9,12,15,18,… includes numbers that are multiples of 3. Each number is 3 more than the previous one.

2. Starting at 10 and Increasing by 5: The sequence 10,15,20,25,… starts at 10, with each number increasing by 5.

In the first sequence, each term is 3 times a whole number. In the second sequence, each term starts at 10 and adds 5 each time. Both sequences show how regular patterns can be created with simple rules.

Benefits of NCERT Solutions for Class 6 Maths Chapter 1 Exercise 1.4 Patterns in Mathematics

• The exercise helps students see and understand different patterns in numbers, which is key for learning more advanced math topics later.

• By working on problems with number sequences, students get better at solving math problems and using logical thinking.

• Learning about basic patterns and sequences helps with more complicated math topics that come up later.

• Solving number sequences helps students think more clearly and spot relationships between numbers.

• Successfully working through exercises helps students feel more confident in their maths skills and ready for tougher problems.

Class 6 Maths Chapter 1: Exercises Breakdown

Important Study Material Links for Class 6 Maths Chapter 1 - Patterns in Mathematics

Conclusion

NCERT Solutions for Class 6 Maths Chapter 1 Exercise 1.4, "Relations among Number Sequences," helps students learn how different number sequences are related. The clear explanations provided in the solutions make it easier for students to understand and work with these relationships. Practising these exercises improves their ability to see connections between sequences and strengthens their problem-solving skills. With the solutions available as a FREE PDF download, students can study and review at their own pace, making learning more convenient and effective.

Chapter-wise NCERT Solutions Class 6 Maths

The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Related Important Links for Class 6  Maths 

Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.