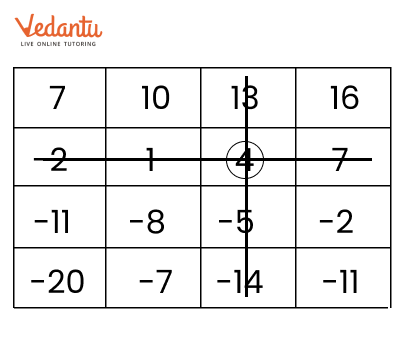
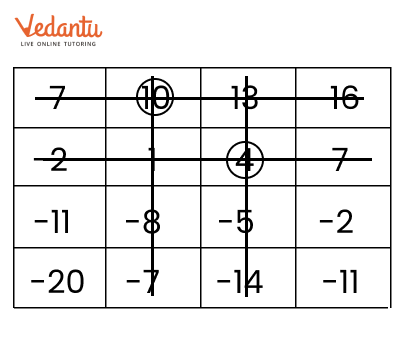
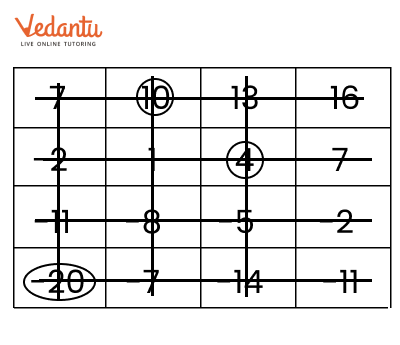
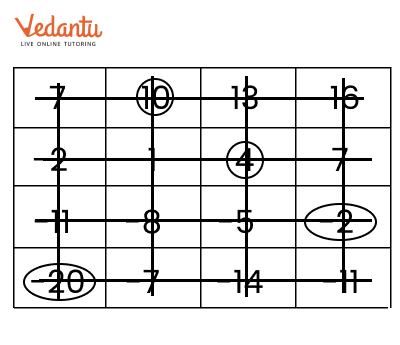
NCERT Solutions for Chapter 10 The Other Side of Zero Class 6 Maths Exercise 10.4 - FREE PDF Download
FAQs on NCERT Solutions for Class 6 Maths Chapter 10 - The Other Side of Zero Exercise 10.4
1. What is Chapter 10 about in NCERT Class 6 Maths?
Chapter 10 explores the concept of integers, focusing on both positive and negative numbers and their operations.
2. How can Vedantu NCERT Solutions help me with Exercise 10.4?
Vedantu NCERT Solutions provides step-by-step explanations that make it easy to understand and solve problems related to integers.
3. What topics are covered in Exercise 10.4 of NCERT Class 6 Maths?
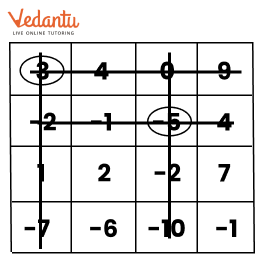
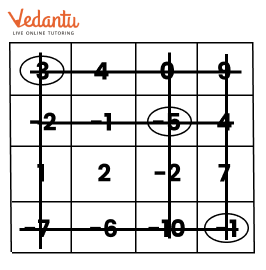
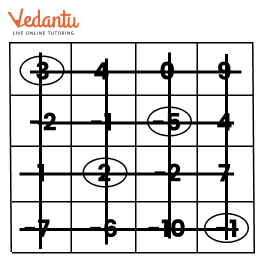
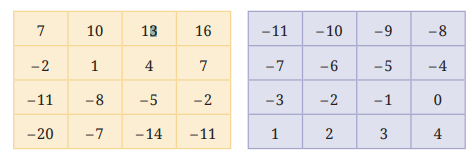
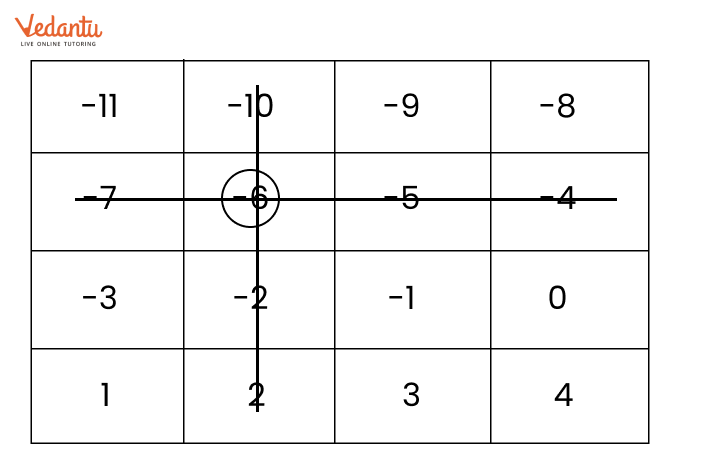
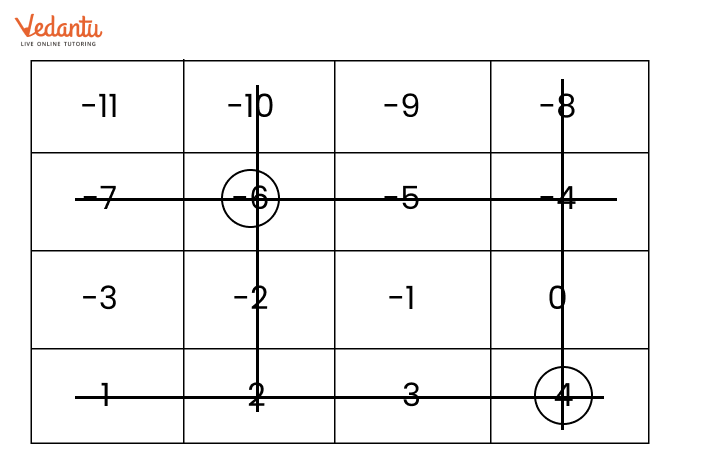
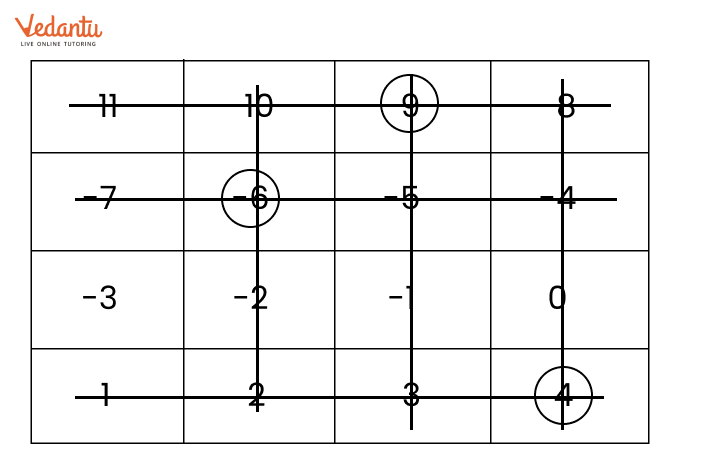
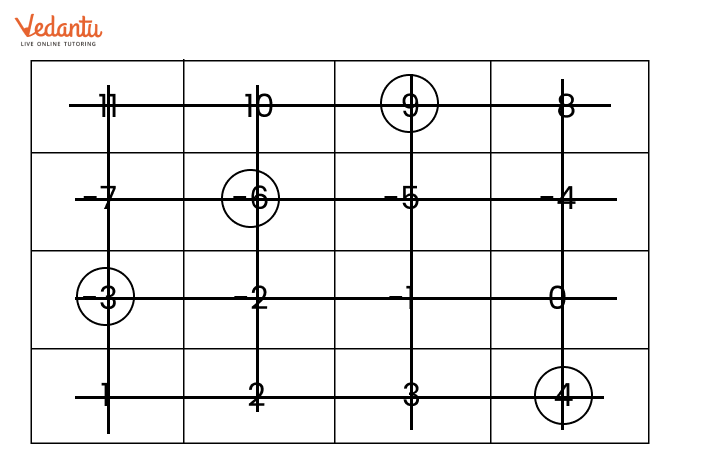
Exercise 10.4 covers addition and subtraction of integers using number lines, along with practical examples.
4. Is it important to learn about integers in Class 6?
Yes, understanding integers is crucial as they are foundational for more advanced math concepts in later classes.
5. How do the NCERT Solutions simplify integer problems in Class 6?
The solutions break down complex problems into simple steps, helping students follow along easily.
6. What tools do I need to solve Exercise 10.4 in Class 6 Maths?
A number line is helpful for visualising integer operations, along with a notebook and pencil for practice.
7. Can I find real-life examples in the NCERT Solutions for Exercise 10.4?
Yes, the solutions include real-life scenarios to help students understand how integers are used in everyday situations.
8. How does understanding zero help in learning integers in NCERT Class 6 Maths?
Knowing how zero acts as a neutral integer helps students see the balance between positive and negative numbers.
9. Are there practice problems in the Vedantu NCERT Solutions for Chapter 10?
Yes, the solutions provide additional practice problems to reinforce understanding of integer operations.
10. How can I access Vedantu NCERT Solutions for Class 6 Maths Chapter 10?
You can find the solutions on the Vedantu website or app, which offers comprehensive study materials.
11. What is the benefit of using NCERT Solutions for Class 6 Maths?
NCERT Solutions ensures that students are aligned with the curriculum and provides clear explanations for better learning.
12. How can I improve my skills in integers with Vedantu?
Regular practice with Vedantu’s solutions and following the step-by-step methods will enhance your understanding and problem-solving skills in integers.