NCERT Solutions for Class 6 Maths Chapter 14 - In Hindi

ावली 14.1 

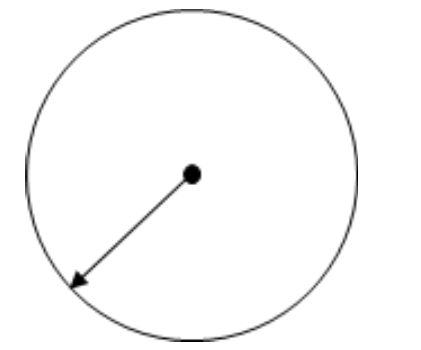
1. \[\text{3}.\text{2}\] से.मी. त्रिज्या वाला एक वृत्त खींचिए। 

उत्तर: 

1. परकार लेकर उससे \[\text{3}.\text{2}\] से.मी. माप बनाइए

2. पेंसिल की नोक से एक बिन्दु बनाइए, जिसे ‘O’ नाम दीजिए। 

3. परकार के सुई वाले भाग को O पर रखिए। 

4. अब पेंसिल वाले भाग को धीरे धीरे घूमते हुए वृत्त बनाइए। 

2. एक ही केंद्र ‘O’ को लेकर \[\text{4}\] से.मी. और \[\text{2}.\text{5}\] से.मी. त्रिज्या वाले दो वृत्त खींचिए। 

उत्तर: 

1. परकार लेकर \[\text{4}\] से.मी. माप लीजिए। 

2. एक बिन्दु को नाम O दीजिए

3. O बिन्दु वृत्त का केंद्र होगा, परकार की सुई वाला भाग केंद्र पर रखकर पेंसिल वाले भाग से घुमाते हुए वृत्त बनाइए। 

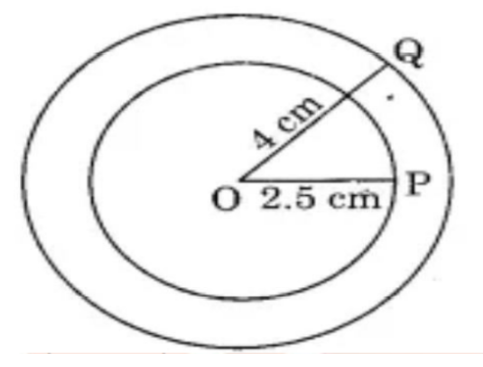
4. अब \[\text{2}.\text{5}\] से.मी. त्रिज्या लेकर इस प्रकार वृत्त बनाइए। 

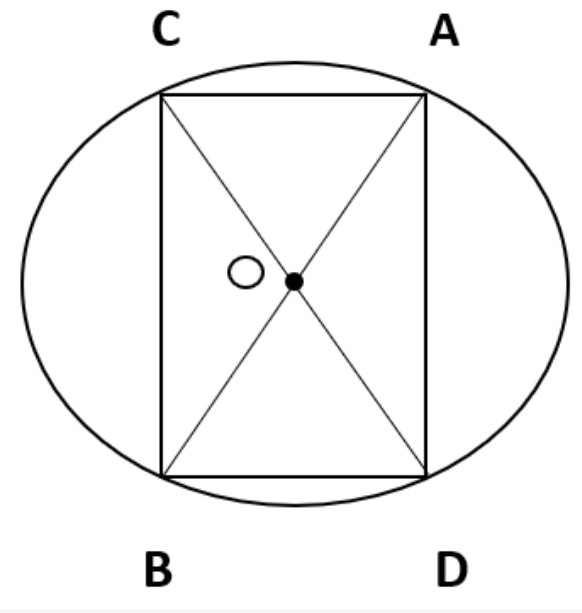
3: एक वृत्त और उसके कोई दो व्यास खींचिए. यदि आप इन व्यासों के सिरों को जोड़ देतो कौनसी आकृति प्राप्त होगी? आप इन उत्तर की जांच किस परकार करेंगे?

उत्तर: 

विवरण - O केंद्र से एक वृत्त खींचकर उसमें दो व्यास बनाए जिन्हें नाम दिया AB तथा CD। यदि इन व्यासों के सिरों को मिला दिया जाए, तो एक आकृति बनेगी जो एकआयात होगी, इस बात को हम निम्नलिखित रूप में सिद्ध करेंगे। 

O केंद्र है तथा व्यास AB तथा CD को प्रतिछेदित बिन्दु भी है। 

इसलिए 

OC = OD तथा OA = OB

(एक ही वृत्त की सामान त्रिज्याए) 

CB= AD तथा AC = DB

केंद्र के सम दुरी पर स्थित जिवाएं सामान होती है। 

∠A =∠ B = ∠ C=∠ D= \[\text{9}0\] °

(∆ACB तथा ∆ADB है) 

(∆CBD तथा ∆CAD सर्वांगसम है। ) 

 इसलिए ∠A, ∠ B, ∠ C, ∠ D सर्वांगसम है। 

चतुर्भुज के चारो कोण सामान हो तो एक कोण का माप \[\text{9}0\] ° होता है। 

इसलिए यह एक आयत है (सम्मुख भुजाएं सामान होती है तथा प्रत्येक कोण \[\text{9}0\] ° का है) 

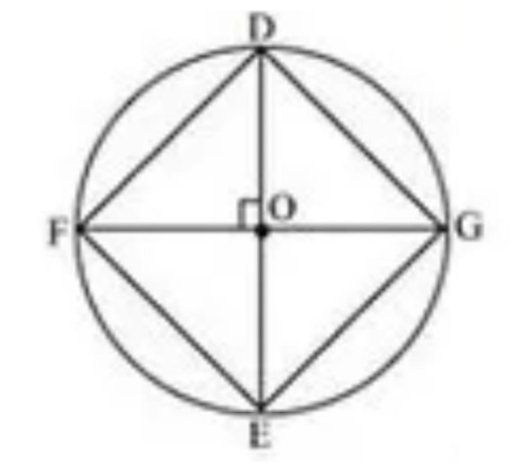
यदि व्यास परस्पर लंब हो तो सिरों को मिलने से प्राप्त आकृति एक वर्ग होगी। जांच के लिए हम विवरण इस प्रकार देंगे। 

DE तथा FG व्यास परस्पर लंब है, तो 

∠FOD, ∠GOD, ∠FOE, ∠GOE = \[\text{9}0\] °

व्यास के सिरों को मिलने से को त्रिभुज बनेंगे वे समबाहु त्रिभुज होंगे इसलिए उनसे बना चतुर्भुज होगा अर्थात एक वर्ग होगा। 

4. एक वृत्त खींचिए और बिन्दुA,B,और C इस परकार अंकित कीजिए कि: 

A) A वृत्त पर स्थित हो। 

B) B वृत्त के अभ्यन्तर में स्थित हो। 

C) C वृत्त के बहीर्भाग में स्थित हो। 

उत्तर: 

1. एक नोकीली पेंसिल से वह बिन्दु अंकित कीजिये जिसे वृत्त का केंद्र बनाना चाहते है। इससे बिन्दु से मनांकित कीजिये। 

2. परकार को वन्शित त्रिज्या के लिए खेलिए 

3. परकार के नोकीले को घुमाइए और एक चक्कर पूरा कीजिये 

4. वृत्त खींचने को घुमाइए और एक चक्कर पूरा कीजिये

1. वृत्त पर एक बिन्दु अंकित कीजिये A लिखिए। 

2. वृत्त के अंदर एक बिन्दु लीजिए और इससे B लिखिए। 

3. वृत्त के बाहर एक बिन्दु लिखिए और इससे C लिखिए। 

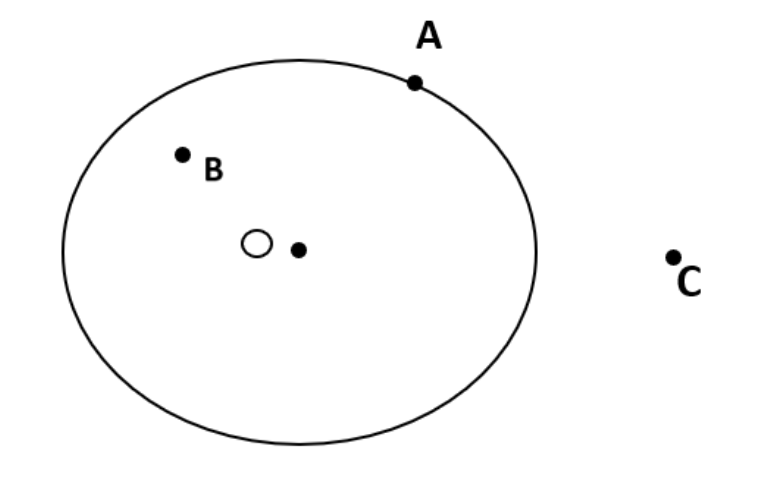
5. मान लीजिएA और B सामान त्रिज्याओ वाले दो वृतो के केंद्र है। इन्हें इस परकार खींचिए ताकि एक वृत्त दूसरे के केंद्र से होकर जाए। इन्हें C तथा D पर प्रतिछेदित करने दीजिए जांच कीजिये की AB और CD परस्पर समकोण पर है। 

उत्तर5: हम परकार से एक त्रिज्या कि माप लेकर पहले एक वृत्त बनाएँगे, इसके केंद्र को A नाम देंगे अब इतनी ही त्रिज्या से दूसरा वृत्तखींचेंगे की B की परीधि A से गुजर कर जाती हो। 

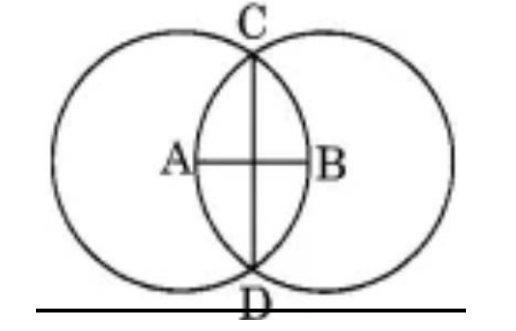
वृत्तA तथा वृत्तB जहाँ मिलते है उसे C तथा D नाम दीजिए अब AB तथा CD को मिलाइए। दोनो जहां मिलते है उस बिन्दु को O नाम दीजिए। 

∠AOC, ∠BOC, ∠AOD, ∠BOD = \[\text{9}0\] °

इस से सिद्ध होता है की AB तथा CD परस्पर समकोण पर है। 

ावली 14.2

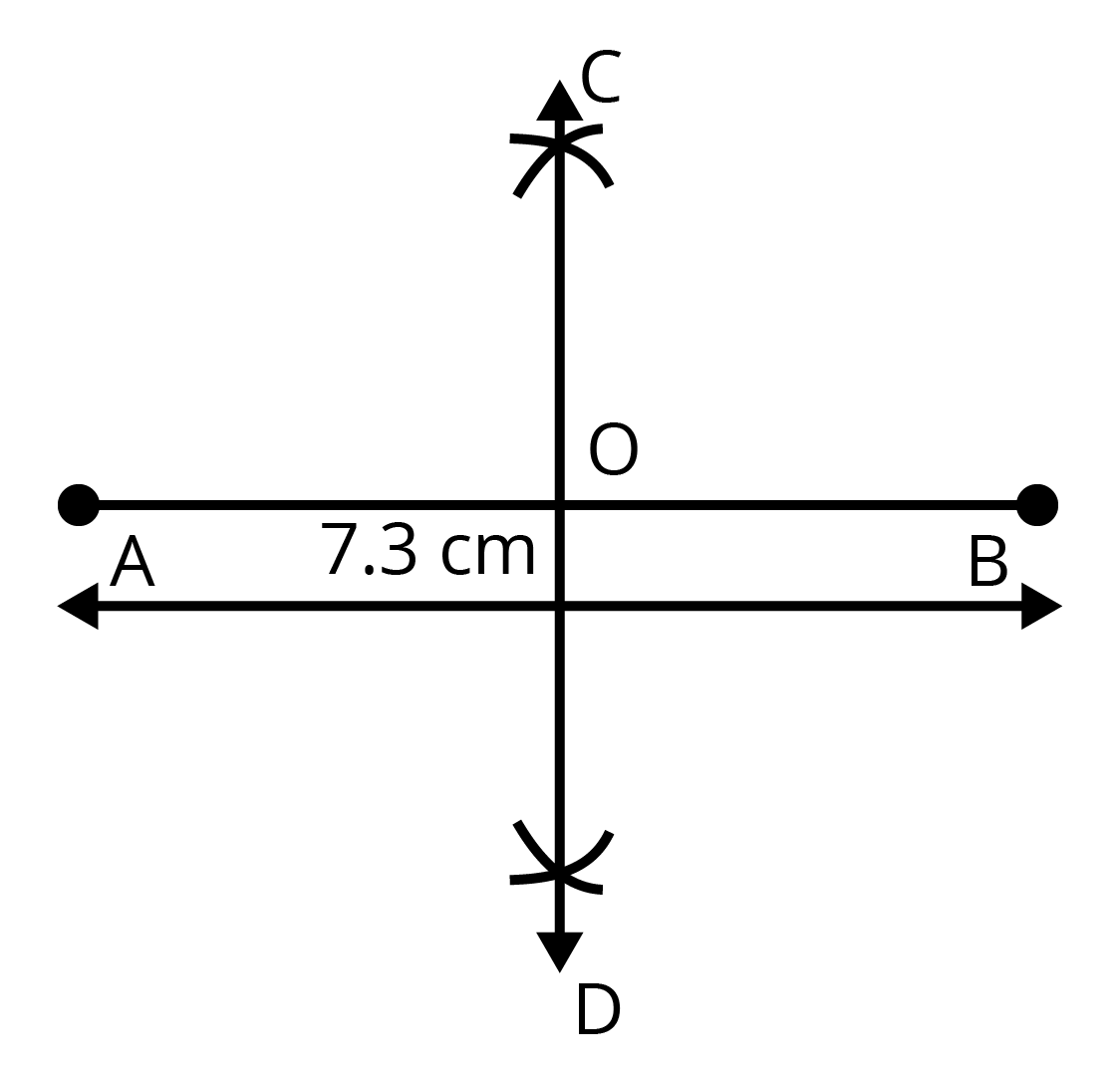
1. रुलर का प्रयोग करके \[\text{7}.\text{3}\] से.मी.लंबाई का एक रेखाखंड खींचिए। 

उत्तर: एक रुलर लीजिए तथा पेंसिल की सहायता से रुलर पर जहा शून्य लिखा है, वहां बिन्दु A बनाइए। अब बिन्दु A से \[\text{7}.\text{3}\] की दूरी पर दूसरा बिन्दु B बनाइए। दोनो बिन्दुओं को गिलने पर रेखा खड AB बन जायगा। 

2. रुलर और परकार का प्रयोग करते हुए 5.6 से.मी. लंबाई का एक रेखाखंड खींचिए। 

उत्तर: एक रेखा खींचिए, उस पर एक बिन्दु A अंकित कीजिये, बिन्दु A पर परकार की सुई की नोक रखकर \[\text{5}.\text{6}\] से.मी. की दूरी पर एक चाप खीच दीजिए , इसे बिन्दु B नाम दीजिए। इस परकार AB रेखाखंड बन गया। 

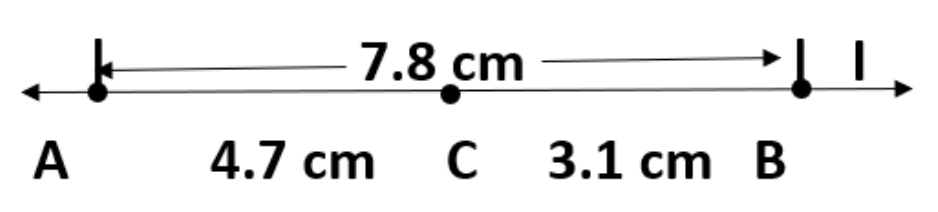
3. \[\text{7}.\text{8}\] से.मी. का रेखाखंडAB खींचिए , इसमें से AC काटिए जिसकी लंबाई \[\text{4}.\text{7}\] से.मी.हो BC को मापिये। 

उत्तर: यदि \[\text{7}.\text{8}\] रेखाखंड में से \[\text{4}.\text{7}\] का रेखाखंड AC कटा जाए तो रेखाखंड BC रह जाता है जिसकी लंबाई होगी \[\text{3}.\text{1}\] से.मी.। 

4. \[\text{3}.\text{9}\] से.मी. लंबाई का एक रेखाखंड अब दिया गयाहै। एक रेखाखंडपा खींचिए जो रेखाखंडAB का दोगुनाहै। 

उत्तर: 

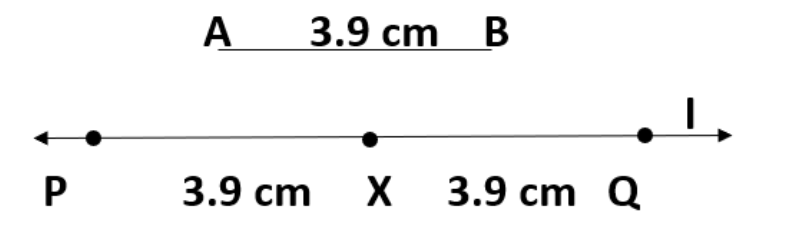
1. एक रेखा खींचे \[\overline{AB}\] 

2.  \[\overline{PX}\] का निर्माण ऐसे करें की \[\overline{PX}\] की लंबाई = \[\overline{AB}\] की लंबाई के बराबर हो

3. फिर \[\overline{XQ}\] की कटोती ऐसी है की \[\overline{PX}\] की लंबाई \[\overline{AB}\] के बराबर है

4. \[\overline{PX}\] की लंबाई और \[\overline{XQ}\] की लंबाई एक साथ जोड़ी गई लंबाई की दोगुनी है.

सत्यापन : 

माप से हम पाते हैं की PQ = \[\text{7}.\text{8}\] से.मी. 

= \[\text{3}.\text{9}\] से.मी. + \[\text{3}.\text{9}\] से.मी. = \[\overrightarrow{AB}\] + \[\overrightarrow{AB}\] = \[2\] × \[\overrightarrow{AB}\] 

5. \[\text{7}.\text{3}\] से.मी. . लंबाई का रेखाखंडAB और \[\text{3}.\text{4}\] से.मी. लंबाई का रेखाखंडCD दिया गयाहै। एक रेखाखंड XY खिचिये ताकि XY की लंबाईAB और CD के अंतरके बराबर हो। 

उत्तर5: 

(Image will be uploaded soon)

1. एक रेखा खिचे उस पर एक बिन्दु X लें

2. XZ का निर्माण ऐसे करें की लंबाई XZ = AB क लंबाई = \[\text{7}.\text{3}\] से.मी. हो

3. फिर ZY = CD की लंबाई = \[\text{3}.\text{4}\] से.मी.काट लें

4. इस परकार XY की लंबाई = AB की लंबाई - CD की लंबाई 

सत्यापन : 

माप से हम XY = \[\text{3}.\text{9}\] से.मी. की लंबाई पाते हैं

= \[\text{7}.\text{3}\] से.मी. - \[3.4\] से.मी. = AB - CD

ावली 14.3

1. कोई रेखाखंड PQ खींचिए। बिना मापहुए PQ के बराबर एक रेखाखंड की रचनाकीजिए। 

उत्तर: PQ एक रेखाखंड दिया गया है जिसकी माप नहीं दी गयी है, उसी माप का एक और रेखाखंड बनाने के लिए हम एक परकार लेकर उसका नुकीला हिस्सा बिन्दु P पर रखेंगे तथा दूसरा पेंसल वाला भाग बिन्दु Q पर रखेंगे। 

अब जितना फैलाव इस परकार का है उितनी दिए गए रेखाखंड की लंबाई है। अब हमें इसी माप का दूसरा रेखाखंड बनाना है। एक रेखा बानाएंगे उस पर एक बिन्दु A अंकित करेंगे परकार को बीना हिलाए उसका नुकीला भाग बिन्दु A पर रखेगे तथा पेंसल वाले से रेखा पर चाप लगाएँगे इसे बिन्दु B नाम देंगे। माप कर देखने पर PQ तथा AB की लंबाई समान होगी। 

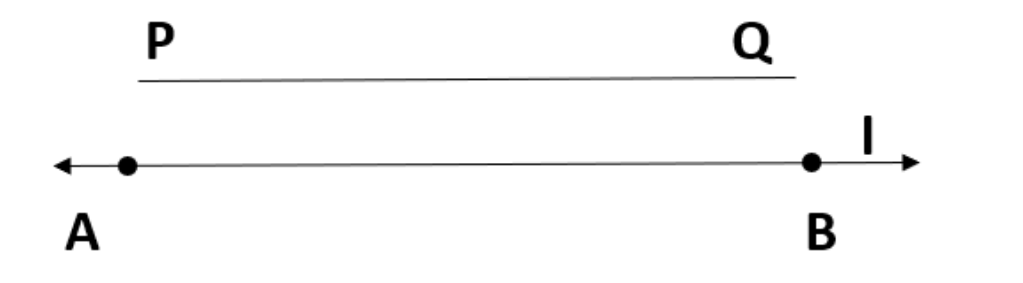
2. एक रेखाखंड AB दियाहुआ है, जिसकी लंबाई ज्ञात नही है। एक रेखाखंड पा की रचनाकीजिए, जिसकी लंबाईAB की लंबाईकी दोगुनीहो। 

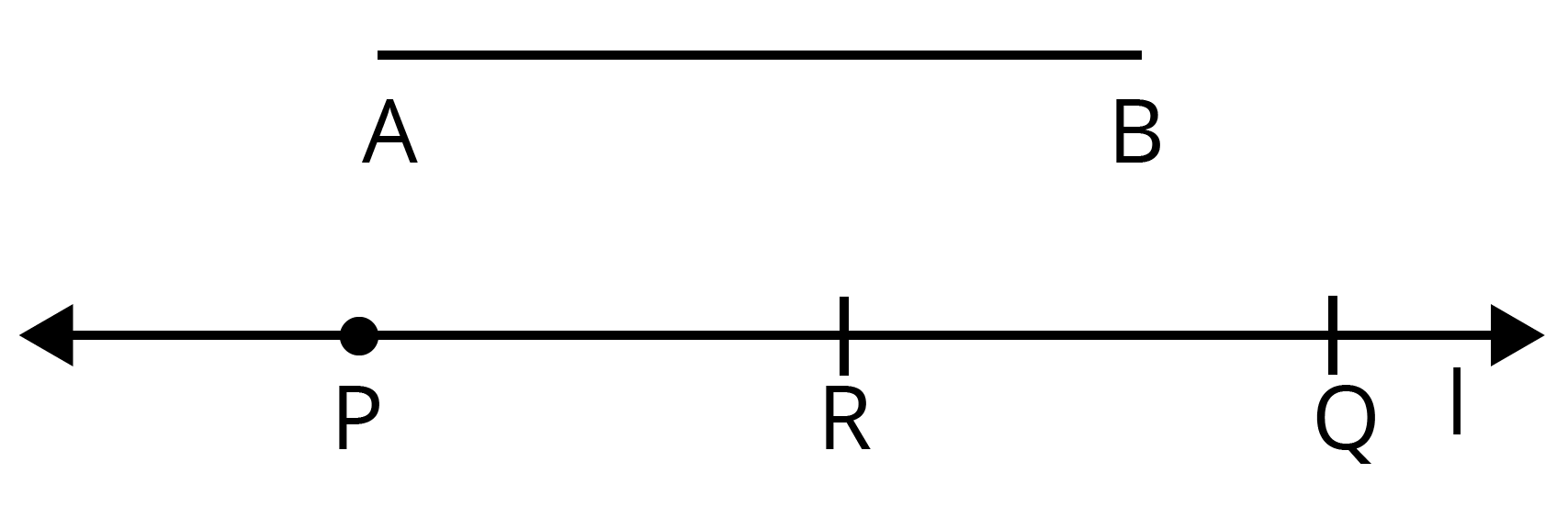
उत्तर: AB दिया गया रेखाखंड है जिसकी लंबाई नही दी गई है। हमें एक रेखाखंड PQ बनाना है जसकी लंबाई AB की लंबाईकी दोगुनी हो। सर्वप्रथम परकार का नुकीला भाग बिन्दु A पर रखेगे पेंसल वाला तथा बिन्दुB पर रखेंगे। इस परकार का जितना फैलाव होगा उितनीAB की लंबाईहै। 

1. एक दूसरी रेखा खिचेंगे तथा उस पर एक बिन्दु अंकित करेंगे जिसे P नामदेंगे। 

2. अबP बिन्दुपर परकार का नुकीला भाग रखकर पेंसल वाले भागसे रेखा पर एक चाप बनाएँगे , इस प्रक्रिया में परकार को बिना हिलाए चाप खींचना है। 

3. जहा पर चाप खिंची वहा बिन्दुR अंकित करना है। 

4. अब बिन्दु R पर परकार का नुकीला भाग रखकर जहा पेंसल वाला भाग रेखा को छूता है, वहा चाप खिचेंगे उस बिन्दुको Q नाम देंगे

5. यदि अब की लंबाई नापेंगे तथा PQ की लंबाई नापेंगे हम देखेंगे की PQ लंबाई, AB की लंबाई से दुगुनी है। 

ावली 14.4

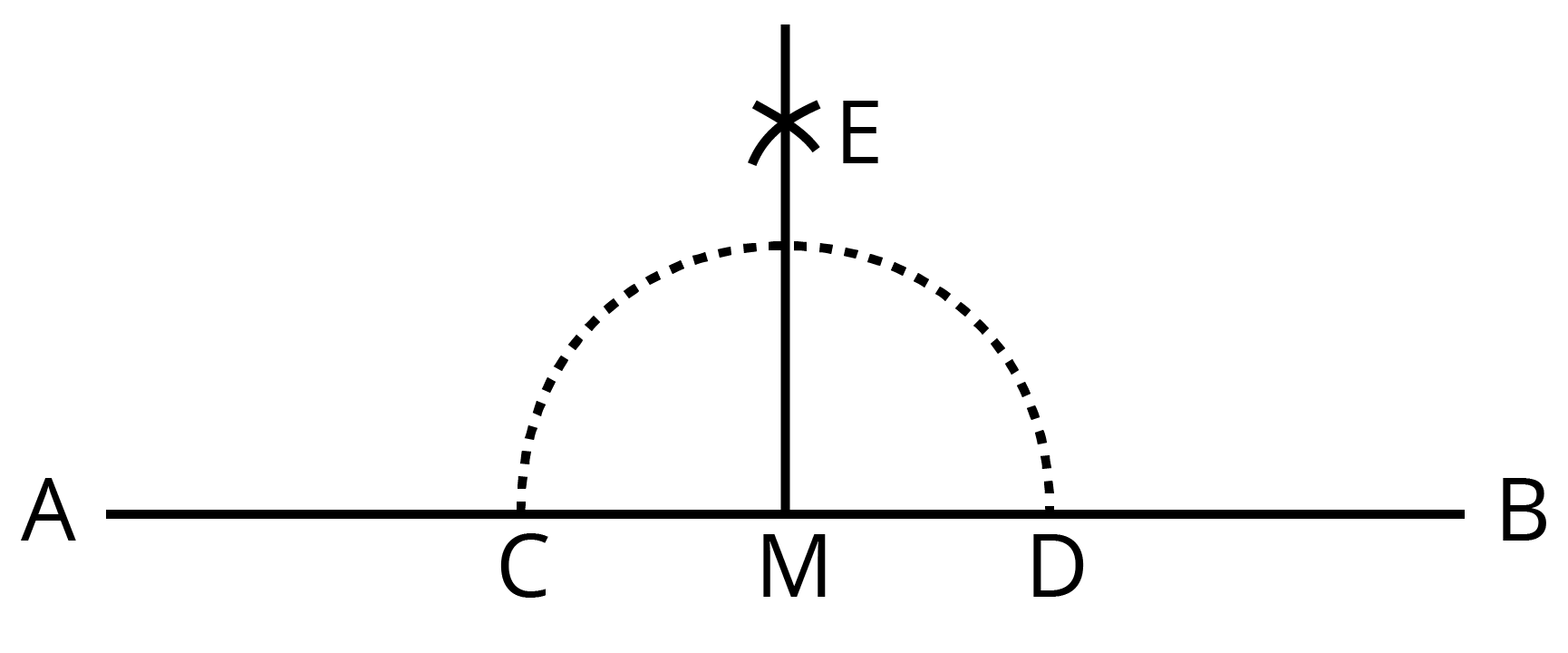
1. एक रेखाखंड AB खींचिए। इस पर कोई बिन्दु m अंकित कीजिये। M से होकर AB पर एक लंब, रुलर और परकार द्वारा खींचिए। 

उत्तर: 

1.  एक रेखाखंड AB खींचिए, उसपर कोई बिन्दु M लीजिए। 

2. अब बिन्दु M को केंद्र लेकर त्तथा उचित त्रिज्या लेकर रेखाखंड AB पर दो चाप खींचिए जिन्हें C तथा D नाम दीजिए। 

3. अब बिन्दु C तथा D को केंद्र लेकर तथा त्रिज्या CM से अधिक हो, दो चाप खींचिए। इसे E नाम दीजिए। 

4. अब E बिन्दु से M बिन्दु को मिला लीजिए। EM रेखाखंड AB पर लंब है। 

2. एक रेखाखंड PQ खींचिए। कोई बिन्दुR लीजिएजो PQ पर न हो। R से होकर PQ पर लंब खींचिए। 

(रुलर और सेटस्केयर द्वारा)

उत्तर: 

1.  एक रेखाखंड PQ खींचिए, कोई बिन्दु R लीजिए जो PQ पर न हो। 

2. सेटस्क्वेयर को PQ पर इस परकार रखिए की \[\text{9}0\] ° बनाने वाली एक भुजा PQ पर रहे। 

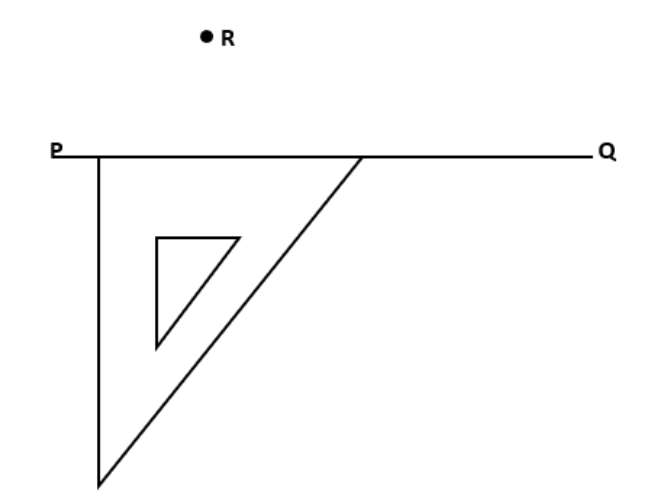
3. अब सेटस्क्वेयर की तिरछी भुजा पर रुलर रखिए। 

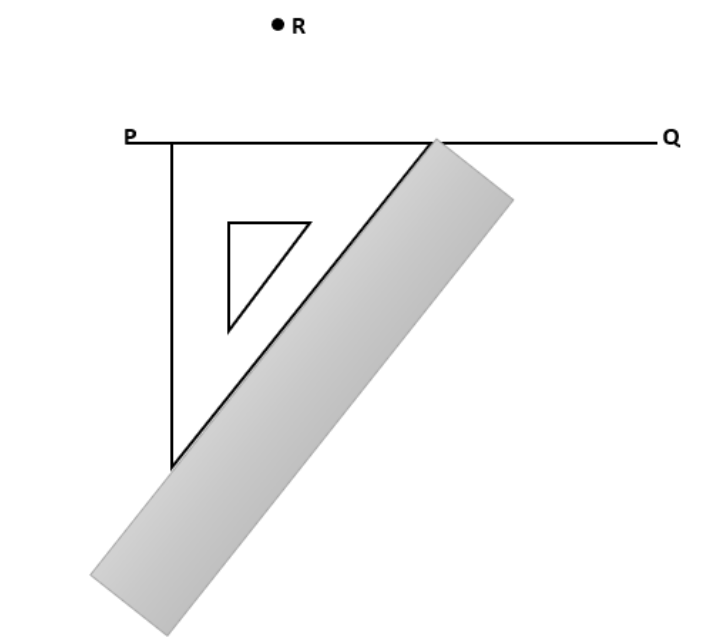
4. रुलर को पक्का पकड़कर सेटस्क्वेयर को धीरे धीरे ऊपर लेते जाए। 

5. सटस्क्वेयर पर R बिन्दु से PQ पर लंब खींचिए। 

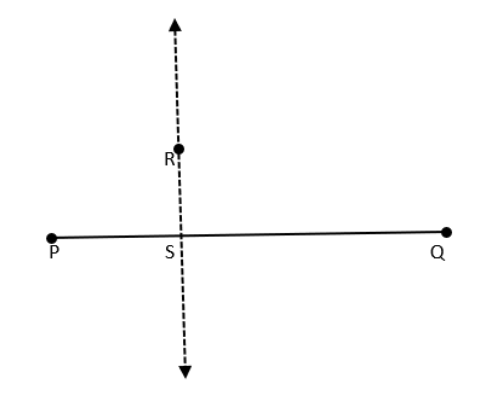
3. एक रेखा I खींचिए , और उस पर स्तिथएक बिन्दुX से होकर , रेखा I  पर एक लंब रेखाखंड XY खींचिए। 

अब Y से होकर रेखाखंडXY पर लंब, रुलर और परकार द्वारा खींचिए। 

उत्तर: 

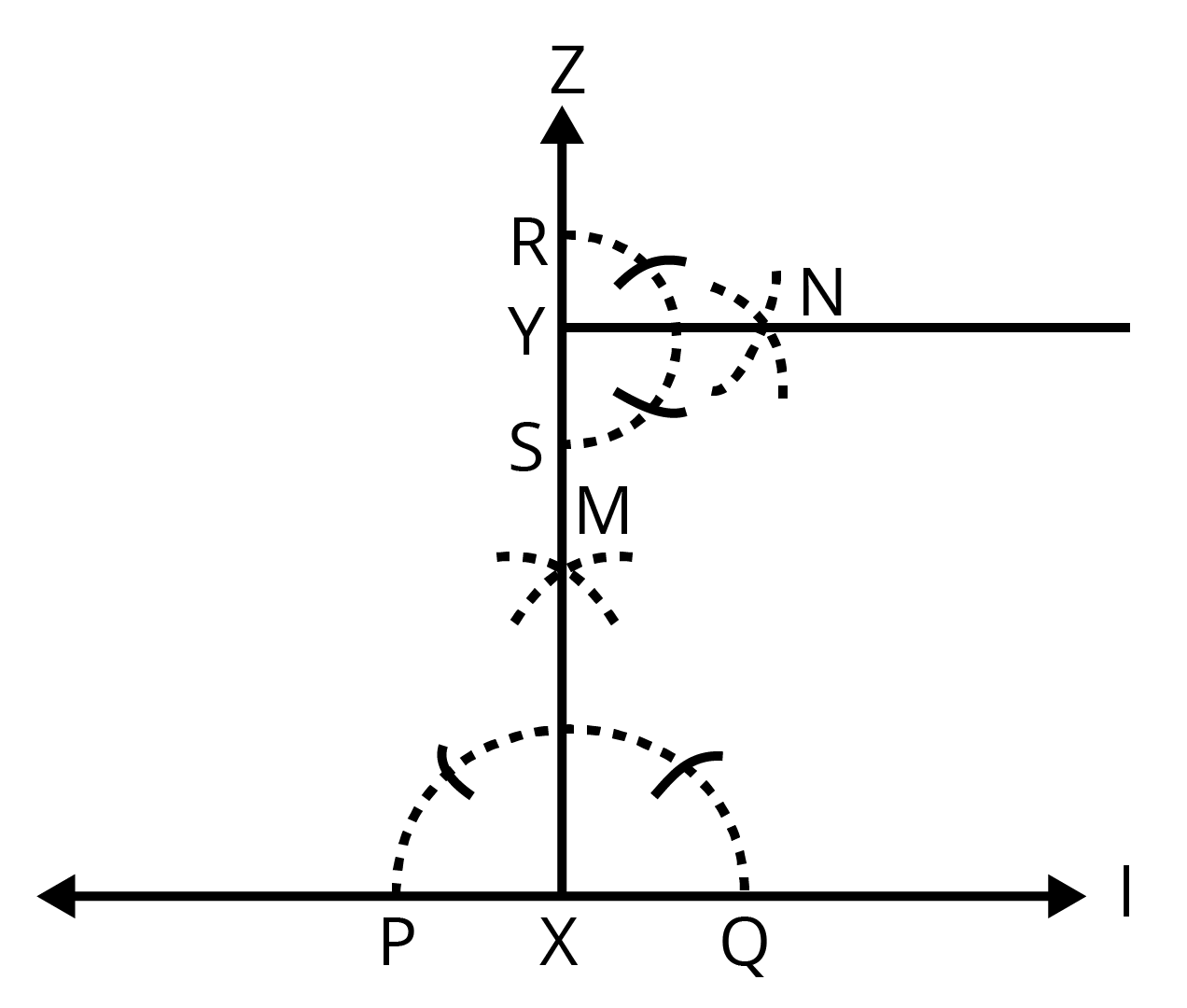
1. एक रेखा I खींचिए, उस पर एक बिन्दु X लेकर रेखाखंड XM बनाइए। 

2. X को केंद्र लेकर रेखाखंड XM पर उचितत्रिज्या लेकर दो चाप खींचिए, जिन्हें बिन्दु A तथा बिन्दु B नामदीजिए। 

3. अब A तथाB को केंद्र लेकर तथाAX से बड़ी त्रिज्या लेकर दो चाप बनाए। चाप जहा मिलतेहै, उसे Y नाम दे। Y को X से मिला दे। 

 XY रेखाखंड XM पर लंब है। 

ावल 14.5 

1. \[\text{7}.\text{3}\] से.मी.लंबाई का एक रेखाखंड AB खींचिए और उसकी सममित अक्ष ज्ञात कीजिये। 

उत्तर. AB का सममित अक्ष, AB का लंब समद्विभाजक होगा। अतः, हम AB का लंब समद्विभाजक बनाते हैं। 

रचना के पद: 

(Image will be uploaded soon)

1. एक रेखाखंड AB - \[\text{7}.\text{3}\] से.मी. खींचा। 

2. बिन्दुओं A और B को केंद्र मानकर तथा AO से अधिक त्रिज्या लेकर दो चाप लगाए जो एक दूसरे को परस्पर बिन्दु C और D पर काटते हैं। 

3. बिन्दुओं C और D को मिलाया। 

4. रेखा CD ही रेखाखंड AB की सममित अक्ष है। 

उत्तर: रचना के पद: 

(Image will be uploaded soon)

1. एक रेखाखंड AB= \[\text{9}.\text{5}\] से.मी. खींचा। 

2. बिन्दुओं A और B को केंद्र मानकर तथा AO से अधिक त्रिज्या लेकर दो चाप लगाए जो एक दूसरे को परस्पर बिन्दु C और D पर काटतेहैं। 

3. बिन्दुओं C और D को मिलाया। 

4. रेखाखंड CD ही रेखाखंड AB का लंब समद्विभाजक है। 

2. \[\text{9}.\text{5}\] से.मी.लंबा एक रेखाखंड खींचिए और उसका लंबसमद्विभाजकखींचिए। 

उत्तर. रचना के पद: 

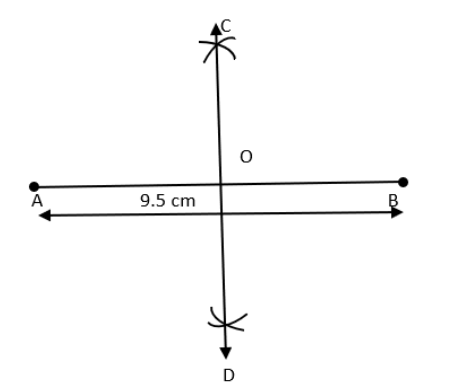
1. एक रेखाखंड XY= \[0.\text{3}\] से.मी. खींचा। 

2. बिन्दुओं X और Y को केंद्र रखकर तथा XP से अधिक त्रिज्या लेकर दो चाप लगाए जो एक दूसरे को परस्पर बिन्दु C और D पर काटते हैं। 

3. बिन्दुओं C और D को मिलाया। 

4. रेखाखंड CD ही रेखाखंड XY का लंब समद्विभाजक है। 

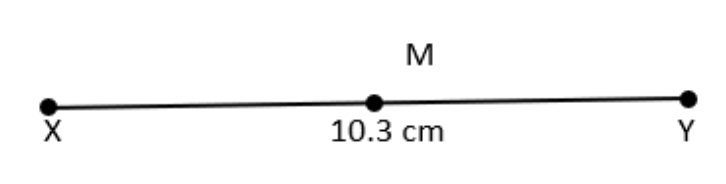
अब: 

1. बिन्दु \[\text{7}\] लंब समद्विभाजक पर स्तिथ है। मापन द्वारा, PX=PY है। 

2. यदि M रेखाखंड XY, का मध्यबिन्दु है तो MX= \[\frac{1}{2}\] XY होगा। 

रचना के पद: 

1. एक रेखाखंड AB= \[\text{12}.\text{8}\] से.मी. खींचा। 

2. रेखाखंड AB का लंब समद्विभाजक खींचा जो बिन्दु C पर मिलता है। अतः, बिन्दु C रेखाखंड AB का मध्य बिन्दु है। 

3. अब, रेखाखंड AC का लंब समद्विभाजक खिंचा जो बिन्दु D परमिलता है। अतः, बिन्दु D रेखाखंड AC का मध्य बिन्दु है। 

4. पुनः, रेखाखंड CB का लंब समद्विभाजक खिंचा जो बिन्दु E पर मिलता है। अतः, बिन्दु E रेखाखंड CB का मध्य बिन्दु है। 

5. इस परकार C, D और E रेखाखंड AB को चार बराबर भागो में विभाजित करते हैं। 

6. मापन द्वरा हमे AD=DC=CE=EB= \[\text{3}.\text{2}\] से.मी. प्राप्त होता है। 

3. एक रेखाखंड XY का लंबसमद्विभाजक खींचिए जिसक लबाई \[\text{1}0.\text{3}\] से.मी. है। 

(a) इस लंबसमद्विभाजक पर कोई बिन्दुP लीजिए। जांचकीजिए कीPX=PY है। 

(b) यदीM रेखाखंड XY का मध्य बींदु है, तो MX और XY केविषय में आप क्या कह सकते हैं?

उत्तर: रचना के पद: 

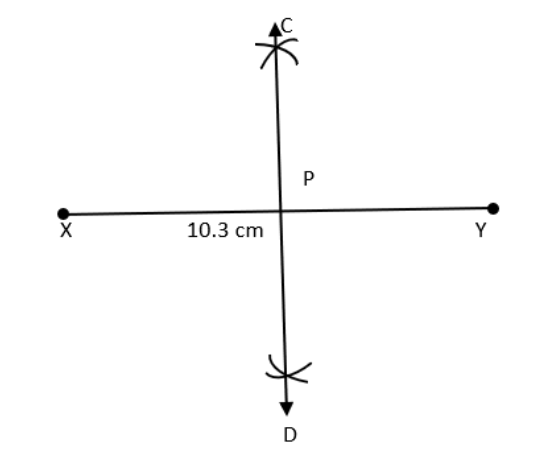
1. एक रेखाखंड PQ= \[\text{6}.\text{1}\] से.मी. खींचा। 

2. रेखाखंड PQ का लंब समद्विभाजक खिंचा जो इसे बिन्दु O पर मिलता है। इस परकार, बिन्दु O रेखाखंड PQ का मध्य बिन्दु है। 

3. बिन्दु O और OP अथवा OQ को त्रिज्या मानकर एक वृत्त बनाया जिसका व्यास PQ है। 

4. लंबाई \[\text{12}.\text{8}\] से.मी. वाला एक रेखाखंड खींचिए। रूलर और परकार कीसहायता से इस के चार बराबर भाग कीजिये। मापन द्वारा अपनी रचना की जांच कीजिये। 

उत्तर: रचना के पद: 

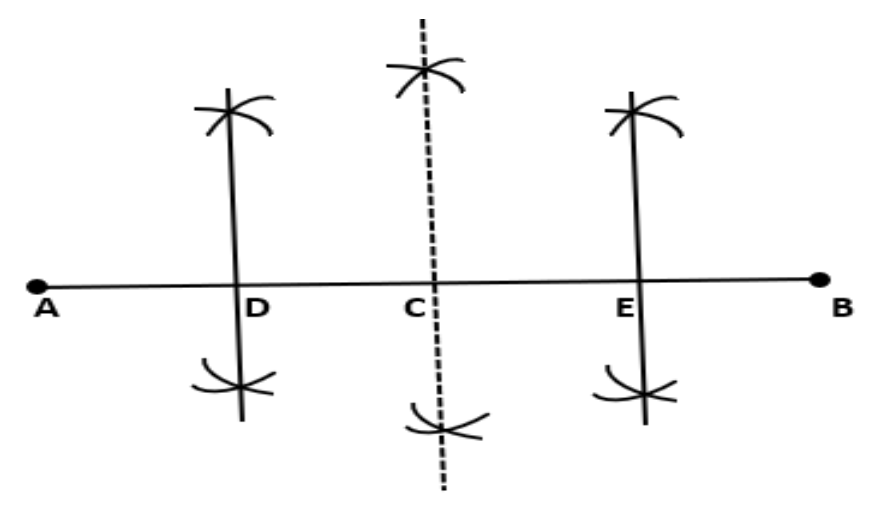
1. बिन्दु C को केंद्र मानकर तथा \[\text{3}.\text{4}\] से.मी. त्रिज्या लेकर एक वृत्त बनाया।

2. जीवा AB खींचा। 

3. बिन्दुओं A और B को केंद्र मानकर तथा AB के आधे से अधिक त्रिज्या लेकर दो चाप लगाएजो एक दूसरे को परस्पर बिन्दु P और Q पर काटते हैं। 

4. बिन्दुओं P और Q को मिलाया। 

5. रेखाखंड PQ ही रेखाखंड AB का लंब समद्विभाजक है। 

6. रेखाखंड AB का लंब समद्विभाजक केंद्र C से होकर जाता है। 

5. \[\text{6}.\text{1}\] से.मी.लंबाई का एक रेखाखंड PQ खींचिए और फिर PQ को व्यास

मानकरएक वृत्त खींचिए। 

उत्तर: रचना के पद: 

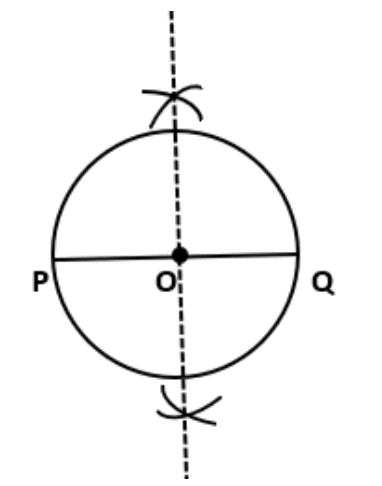
1. बिन्दु C को केंद्र रखकर और त्रिज्या \[\text{3}.\text{4}\] से.मी. का एक वृत्त खींचा। 

2. व्यास AB बनाया। 

3. बिन्दुओं A और B को केंद्र मानकर तथा AB के आधे से अधिक त्रिज्या लेकर दो चाप लगाए जो एक दूसरे को परस्पर बिन्दु P और Q परकाटते हैं। 

4. बिन्दुओं P और Q को मिलाया। 

5. रेखाखंड PQ ही रेखाखंड AB का लंब समद्विभाजक है। 

6. इस स्थिति, रेखाखंड AB का लंब समद्विभाजक केंद्र C सेहोकर जाता है। 

6. केंद्र ब् और त्रिज्या \[\text{3}.\text{4}\] से.मी. लेकर एक वृत्त खींचिए। इसकीकोई जीवाAB खींचिए। इस जिवा AB का लंबसमद्विभाजक खींचिए। जांच कीजियेकीक्या यह वृत्त के केंद्र C से होकर जाता है। 

उत्तर: रचना के पद: 

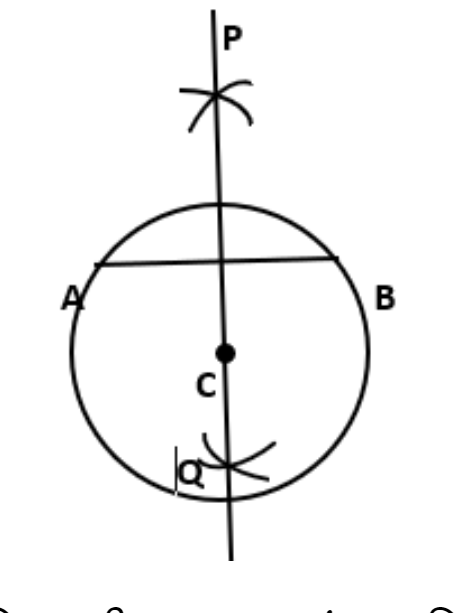
1. बिन्दु O को केंद्र मानकर और त्रिज्या \[\text{4}\] से.मी. लेकर एक वृत्त बनाया। 

2. दो जिवाएं AB और CD खींची। 

3. बिन्दुओं A और B को केंद्र मानकर तथा AB के आधे से अधिक त्रिज्या लेकर दो चाप लगाए जो एक दूसरे को परस्पर बिन्दु E और F पर काटतेहैं। 

4. बिन्दुओं E और F को मिलाया। 

5. रेखाखंड EF रेखाखंड AB का लंब समद्विभाजक है। इस परकार, रेखाखंड GH रेखाखंड CD का लंब समद्विभाजक है। 

6. ये दोनों लंब समद्विभाजक बिन्दु O पर मिलते हैं जो की वृत्त का केंद्र है। 

7.\[\text{6}\] को उस स्थितिवेफ के लिएदोबारा कीजियेजब AB एक व्यास है। 

उत्तर 7: रचना के पद: 

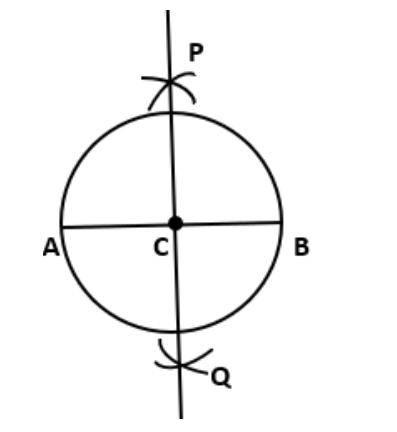
1. एक कोण बनाया जिसका एक शीर्ष O है। 

2. उसकी एक भुजा पर एक बिन्दु A और दूसरी भुजा पर बिन्दु B इस प्रकार बनाया ताकि OA=OB हो। 

3. रेखाखंड OA और OB के लंब समद्विभाजक खींचे। 

4. ये लंब समद्विभाजक बिन्दु P पर मिलते हैं। 

5. PA और PB को मिलाया। 

6. मापन द्वारा ज्ञात होता है कि PA=PB

8. 4 से.मी. त्रिज्या का एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन दोनों जिवाओ का लंबसमद्विभाजक खींचिए। ये कहाँ मिलते हैं? 

उत्तर: 

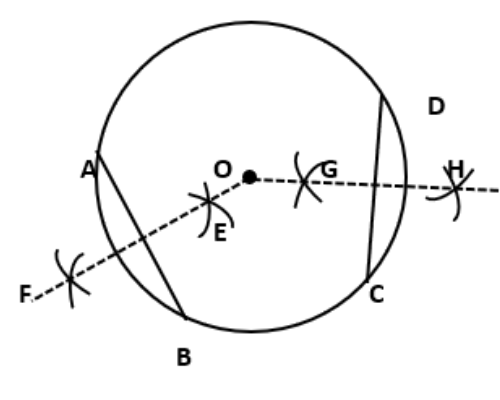
9. शीर्षO वाला कोई कोण खींचिए। इसकी एक भुजा पर एक बिन्दु A और दूसरी भुजा पर एक अन्य बिन्दु B इस परकार लीजिए की OA=OB है। OA और OB के लंबसमद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिछेदित करते हैं क्या PA=PB है?

उत्तर: 

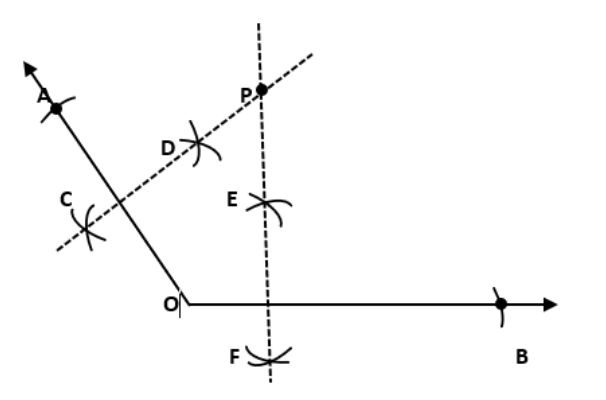
ावली 14.6

1. \[\text{75}\] ° माप वाले कोण ∠POA क रचना कीजिये और इसकी सममितअक्ष खींचिए। 

उत्तर: 

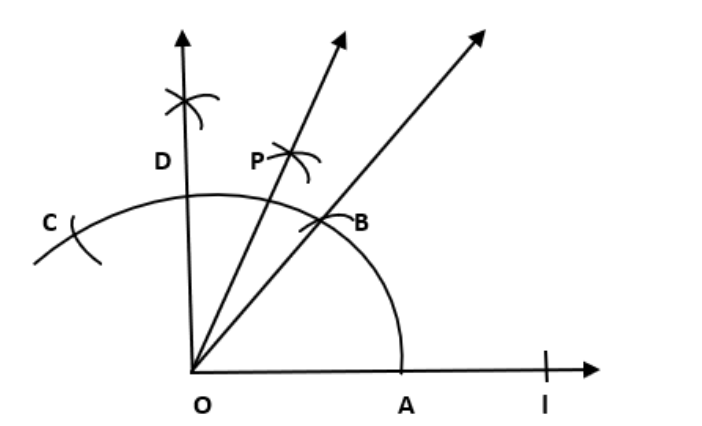
चरण 1 एक रेखा खींचिए, उस पर एक बिन्दु O अंकित कीजिये। 

चरण 2 परकार का नुकीला सिरा O पर रखकर और एक सुविधाजनक त्रिज्या लेकर एक चाप लगाइए जो रेखा को A पर प्रतिच्छेद करे। 

चरण 3 परकार को फैलाव मैं बिना परिवर्तन किये और नुकीले सीरे को A को केंद्र मान कर एक चाप लगाइए जो पिछ्ले चाप को B पर कटता है। 

चरण 4 अब OB को मिलाइए,∠BOA = \[60\] ° 

चरण 5 परकार को फैलाव मैं बिना परिवर्तन किये और नुकीले सिरे को B को केंद्र मानकर एक चाप लगाइए जो पिछ्ले चाप को C पर कटता है। 

चरण 6 कोण ∠BOC का समद्विभाजक खींचिए जो पहले चाप को बिन्दु D पर कटता है अतः, ∠DOA = \[90\] °। 

चरण 7 कोण ∠DOB का समद्विभाजक 𝑂𝑃 खींचिए। अतः, ∠POA = \[75\] °

2. \[\text{147}\] ° माप वाले एक कोण की रचना कीजिये और उसका समद्विभाजक खींचिए। 

उत्तर 2: 

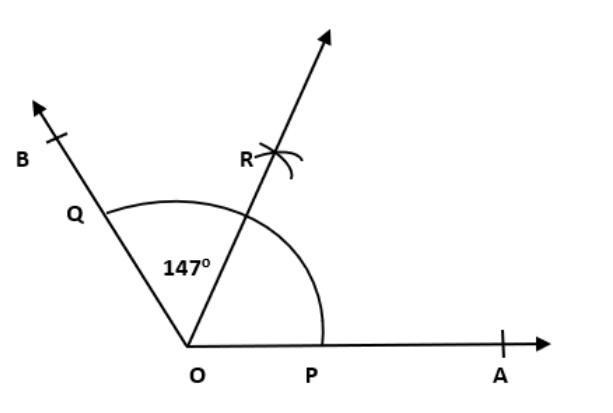
चरण 1 एक रेखा OA खींचे। 

चरण 2 कोण ∠AOB चांदे के सहायता से बनाइए। 

चरण 3 बिन्दु O को केंद्र मानकर और सुविधाजनक त्रिज्या लेकर एक चाप लगाइए। जो रेखा OA और OB को क्रमशः बिन्दु P और Q पर काटे। 

चरण 4 बिन्दु P को केंद्र मानकर और PQ के आधे से अधिक त्रिज्या लेकर एक चाप लगाये। 

चरण 5 बिन्दु Q को केंद्र मानकर त्रिज्या लेकर पहले की चाप पर और एक चाप लगाईये। अब ये दोनो चाप मिलकर R पर काटती है। 

चरण 6 अब OR को मिलाने के लिए एक लकीर खींचिए। 

अतः OR, कोण ∠AOB का समद्विभाजक है। 

3. एक समकोण खींचिए और उसके समद्विभाजककी रचना कीजिये। 

उत्तर: 

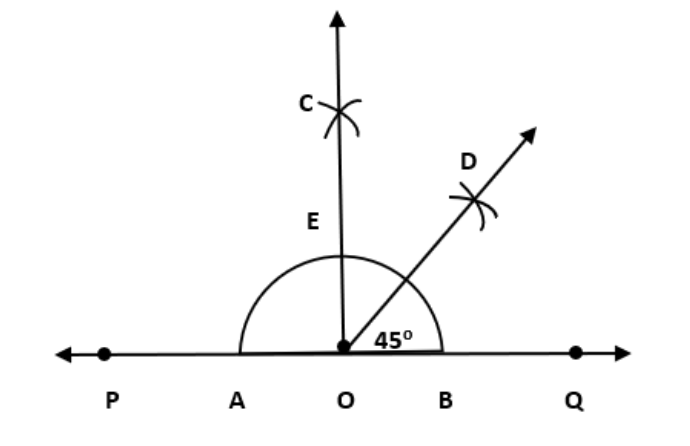
चरण 1 रेखा PQ खींचिए और उस पर बिन्दु O बनाइए। 

चरण 2 बिन्दु O को केंद्र मानकर, त्रिज्या की सहायता से चाप बनाइए जो PQ पर A और B पर काटे। 

चरण 3 बिन्दु A और B को केंद्र मानकर, AB से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर C पर मिलता है। 

चरण 4 OC को मिलाये इस तरह से ∠COQ वांछित समकोण बनी। 

चरण 5 बिन्दु E और B को केंद्र मानकर तथा BE से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर D पर मिले। 

चरण 6 OD को मिलाये, OD कोण ∠COQ का समद्विभाजक है। 

4.\[\text{153}\] ° का एक कोण खींचिए और इसके बराबर भाग कीजिये। 

उत्तर: 

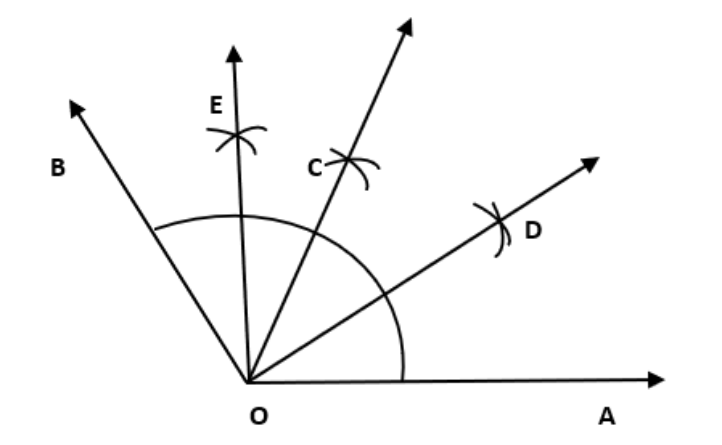
• किरण \[\overrightarrow{OA}\] बनाइए। 

• चांदे के सहायता से ∠AOB = \[\text{153}\] ° बनाईये। 

• कोण ∠AOB का समद्विभाजक \[\overline{OC}\] को खींचिए। 

• कोण ∠AOC का समद्विभाजक \[\overline{OD}\] को खींचिए। 

• कोण ∠BOC का समद्विभाजक \[\overline{OE}\] को खींचिए। 

• अतः \[\overline{OC}\] , \[\overline{OD}\] , \[\overline{OE}\] कोण ∠AOB को चार बरावर भाग मैं विभाजित किया जाता है। 

5. रूलर और परकार की सहायता से निम्न मापों के कोणों की रचनाकीजिये। 

(a) \[\text{6}0\] ° (b) \[\text{3}0\] ° (c) \[\text{9}0\] ° (d) \[\text{12}0\] ° (e) \[\text{45}\] ° (f) \[\text{135}\] ° 

उत्तर: 

(a)

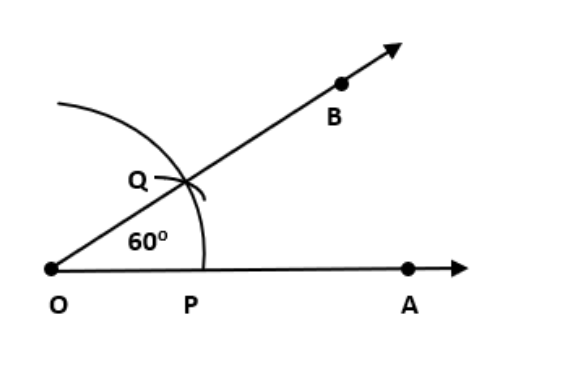
• किरण \[\overrightarrow{OA}\] खींचिए। 

• को केंद्र बिन्दु मानकर \[\overrightarrow{OA}\] पर चाप बनाइए जो P पर परस्पर मिल जाता है। 

• P को अब केंद्र बिन्दु मानकर बिना परकार मैं कोई बदलाव के बिना Q पर एक चाप लगाइए और \[\overrightarrow{OB}\] को खींचिए। अतः ∠AOB = \[\text{6}0\] ° प्राप्त होता है। 

(b)

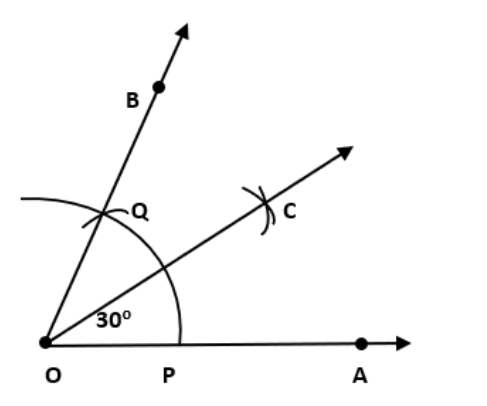
• किरण \[\overrightarrow{OA}\] खींचिए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो \[\overrightarrow{OA}\] के P पर कटती है। 

• बिन्दु P को केंद्र मानकर परकार मैं कोई बदलाव के बिना पहले P के ऊपर एक चाप बनाइए जो Q पर कटती है। 

• OQ को मिलाइए। 

• अब Q और P को केंद्र बिन्दु मानकर और PQ से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर C पर कटती है। 

• अब OC को जुडीये, ∠AOC = \[\text{3}0\] °। 

(c)

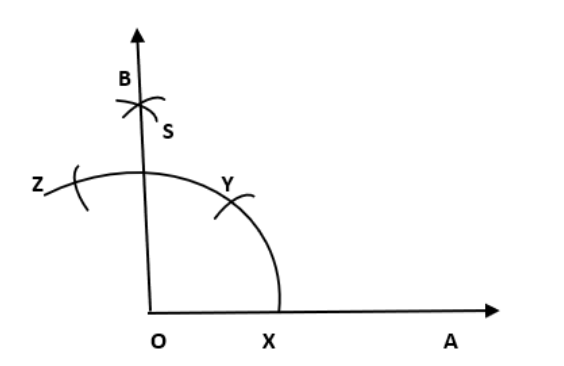
• किरण \[\overrightarrow{OA}\] खींचिए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो \[\overrightarrow{OA}\] के x पर कटती है। 

• बिन्दु x को केंद्र मानकर परकार मैं कोई बदलाव के बिना पहले y के ऊपर एक चाप बनाइए। 

• बिन्दु y को केंद्र मानकर परकार मैं कोई बदलाव के बिना पहले z के ऊपर एक चाप बनाइए। 

• अब y और z को केंद्र बिन्दु मानकर और yz से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर S पर कटती है। 

• अब OS को जोड़िये। 

• अतः ∠AOB = \[\text{9}0\] °

(d)

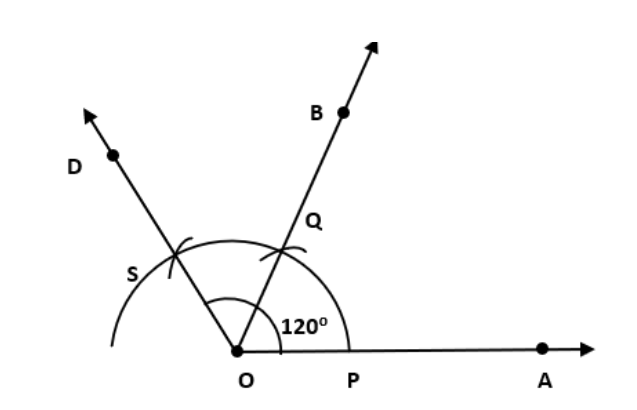
• किरण \[\overrightarrow{OA}\] खींचिए। 

• O को केंद्र मानकर त्रिज्या की सहायता से एक चाप लगाइए जो \[\overrightarrow{OA}\] के ऊपर P पर कटती है। 

• बिन्दु P को केंद्र मानकर परकार मैं कोई बदलाव के बिना पहले Q के ऊपर एक चाप बनाइए। 

• बिन्दु Q को केंद्र मानकर परकार मैं कोई बदलाव केबिना पहले S के ऊपर एक चाप बनाइए। 

• OS को मिलाइए। 

• अतः ∠AOD = \[\text{12}0\] °

(e)

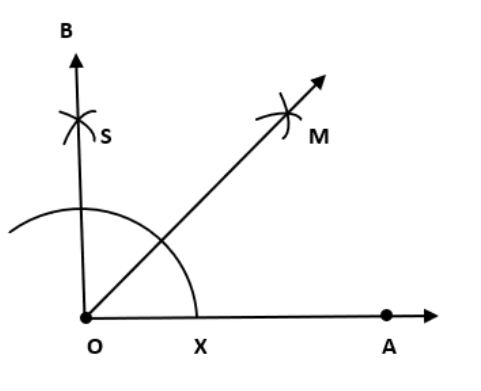
• किरण \[\overrightarrow{OA}\] खींचिए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो \[\overrightarrow{OA}\] के x पर कटती है। 

• बिन्दु x को केंद्र मानकर परकार में कोई बदलाव के बिना पहले y के ऊपर एक चाप बनाइए। 

• बिन्दु y को केंद्र मानकर परकार में कोई बदलाव के बिना पहले z के ऊपर एक चाप बनाइए। 

• अब y और z को केंद्र बिन्दु मानकर और yz से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर S पर कटती है। 

• अब OS को जुड़िये। 

• कोण ∠AOB का समद्विभाजक बनाइए। अतः ∠AOM = \[\text{45}\] °

(f)

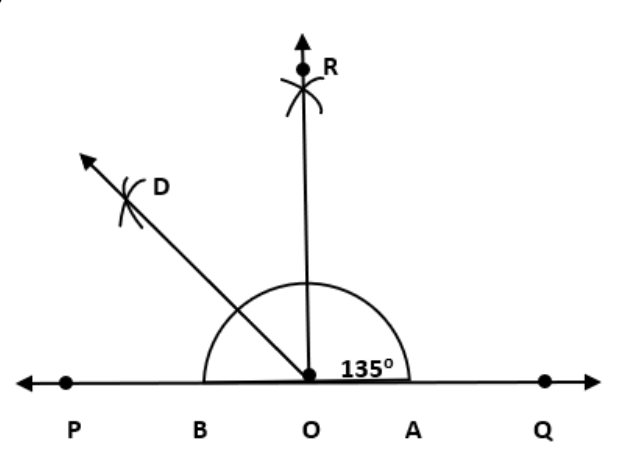
• किरण \[\overleftrightarrow{PQ}\] खींचिए। बिन्दु O को केंद्र बनाइए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो \[\overrightarrow{PQ}\] के A और B पर कटती है। 

• अब A और B को केंद्र बिन्दु मानकर और AB से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर R पर कटती है। 

• OR को जुड़िये। अब ∠QOR = ∠POQ = \[\text{9}0\] °

• कोण ∠POR का समद्विभाजक OD को बनाइए। 

• ∠QOD = \[\text{135}\] °

6. \[\text{45}\] ° का एक कोण खींचिए और उसके सम्द्विभाजितकीजिये। 

उत्तर: 

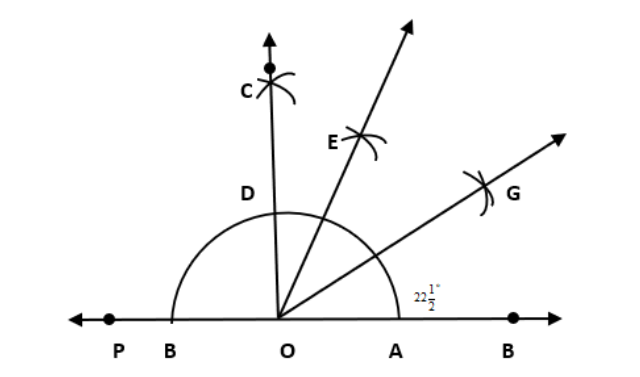
• रेखा PQ बनाइए, उस पर एक बिन्दु O लिए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो \[\overrightarrow{PQ}\] के A और B पर कटती है। 

• अब A और B को केंद्र बिन्दु मानकर और AB से अधिक त्रिज्या लेकर चाप लगाइए जो परस्पर C पर कटती है। 

• OC को जुड़िये। अब ∠COQ = \[\text{9}0\] °

• कोण ∠COE का समद्विभाजक OE को बनाइए। अब ∠QOE = \[\text{45}\] °

• पुनः, कोण ∠QOE का समद्विभाजक OG को बनाइए। अब ∠QOG = ∠EOG = \[22\frac{1}{2}\] °

7.\[\text{135}\] ° का एक कोण खींचिए और उसके सम्द्विभाजितकीजिये। 

उत्तर 7: 

• रेखा PQ बनाइए, उस पर एक बिन्दु O लिए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो \[\overrightarrow{PQ}\] के A और B पर कटती है। 

• अब A और B को केंद्र बिन्दु मानकर और AB से अधिक त्रिज्यालेकर चाप लगाइए जो परस्पर R पर कटती है। 

• OR को जुड़िये। अब ∠QOR = ∠POQ = \[\text{9}0\] °। 

• कोण ∠POR का समद्विभाजक OD को बनाइए। अब ∠QOD = \[\text{135}\] °। 

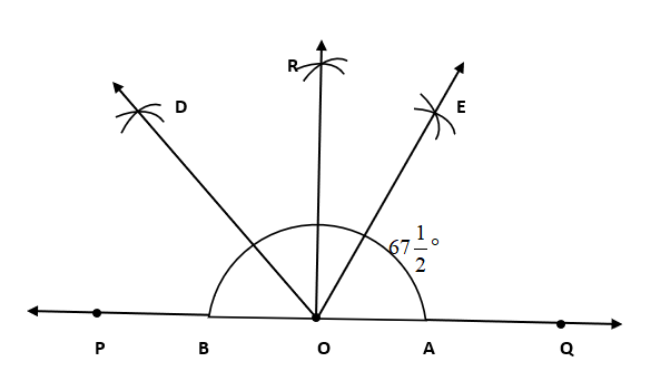
• पुनः, कोण ∠QOD का समद्विभाजक OE को बनाइए। अब ∠QOE = ∠DOE = \[67\frac{1}{2}\] °। 

8. \[\text{70}\] ° का एक कोण खींचिएइस कोण बराबर रूलर और परकार की सहायता से एक कोण बानाइए। 

उत्तर 8: 

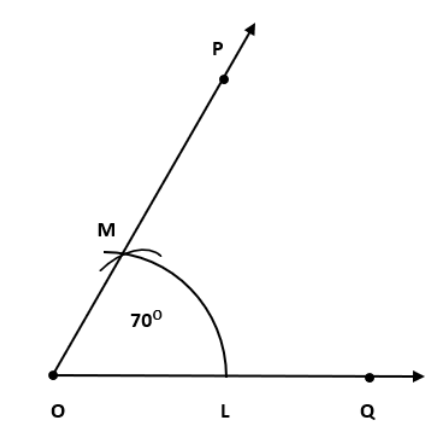
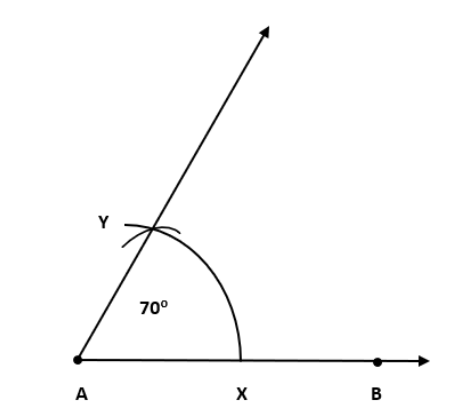
• परकार की सहायता से \[\text{70}\] ° का कोण बनाइए, ∠POQ = \[\text{70}\] °। 

• किरण \[\overrightarrow{AB}\] खींचिए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो ∠POQ के भुजाओ को L और M पर कटती है। 

• बिन्दु A को केंद्र मानकर परकार में कोई बदलाव के बिना पहले AB के ऊपर एक चाप बनाइए जो बिन्दु X पर कटती है। 

• अब, परकार में LM के बराबर त्रिज्या लीजिए। 

• बिन्दु X को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो पहलेचाप को बिन्दु Y पर मिलती है। 

• AY को जुड़िये। अब ∠YAX = \[\text{70}\] °। 

9. \[40\] ° का एक कोण खींचिएइसके संपूरक के बराबर एक कोण बानाइए। 

उत्तर: 

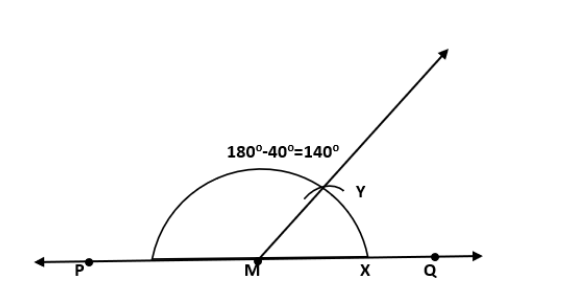
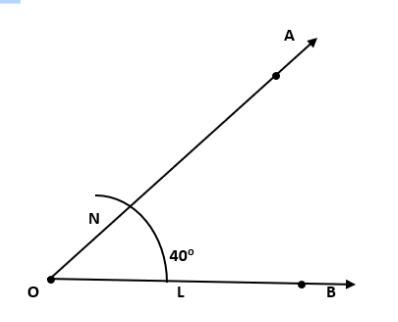
• परकार की सहायता से \[40\] °का कोण बनाइए, ∠AOB = \[40\] °। 

• एक रेखा PQ बनाइए। PQ पर कोई बिन्दु M बनाइए। 

• बिन्दु O को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो ∠AOBके भुजाओ को L और N पर कटती है। 

• बिन्दु M को केंद्र मानकर परकार में कोई बदलाव के बिना पहले MQ के ऊपर एक चाप बनाइए जो बिन्दु X पर कटती है। 

• अब,परकार में LN के बराबर त्रिज्या लीजिए। 

• बिन्दु X को केंद्र मानकर त्रिज्या लेकर चाप लगाइए जो पहलेचाप को बिन्दु Y पर मिलती है। 

• MY को मिलिए। ∠QMY = \[40\] ° और ∠PMY संपूरक कोण है। 

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 6 Maths Chapter 14 solution Hindi mediums are created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 6 Maths Chapter 14 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 6 Maths Chapter 14 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 6 Maths Practical Geometry solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 6 Maths Practical Geometry in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 6 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/ solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 6 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.