Maths Class 6 Chapter 8 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 6 Maths Chapter 8 Playing With Constructions Exercise 8.4 (2025-26)
1. What is covered in Class 6 Chapter 8 Exercise 8.4?
Exercise 8.4 focuses on basic geometric constructions, including the construction of angles and lines.
2. How can I access the Class 6 Chapter 8 Exercise 8.4 NCERT Solutions?
The solutions are available for free download in PDF format, easily accessible online on Vedantu’s website.
3. What are the benefits of using NCERT Solutions for Exercise 8.4?
These solutions provide clear, step-by-step guidance, helping students understand geometric constructions effectively.
4. Are diagrams included in the NCERT Solutions for Exercise 8.4?
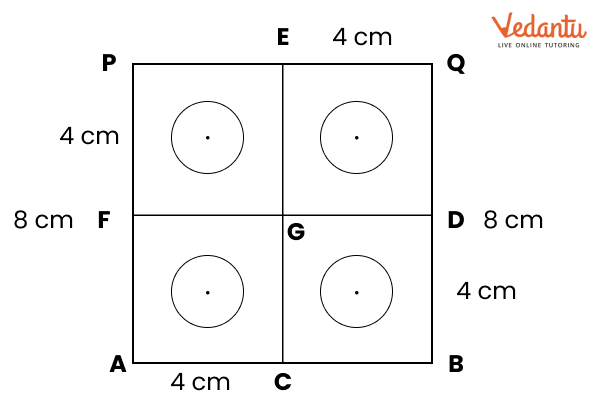
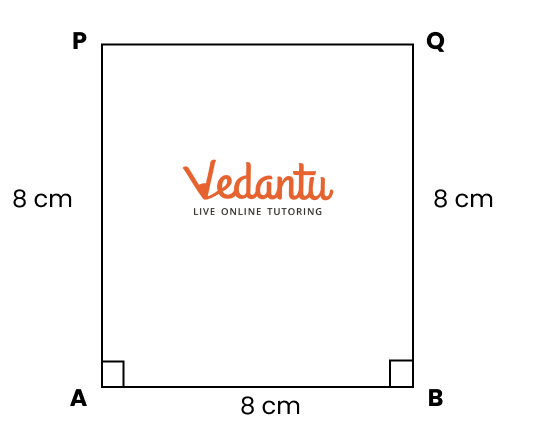
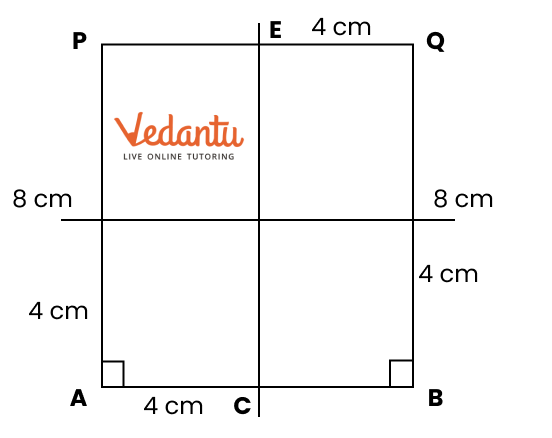
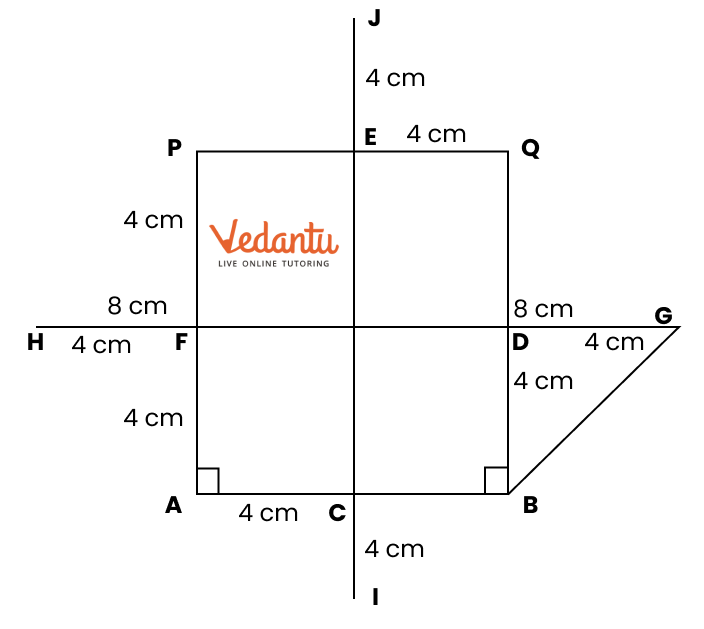
Yes, the solutions feature diagrams to assist students in visualizing the construction processes.
5. How do NCERT Solutions help with exam preparation for Exercise 8.4?
The solutions align with the NCERT syllabus, ensuring that students study relevant material and practice key concepts.
6. What tools are needed for the constructions in Exercise 8.4?
Students will need a compass, a straightedge (ruler), and a pencil to perform the constructions accurately.
7. Can I use the NCERT Solutions for independent study?
Yes, the solutions are designed to support independent learning, allowing students to practice and understand the concepts on their own.
8. How often should I practice with the NCERT Solutions for Exercise 8.4?
Regular practice is recommended to reinforce understanding and improve skills in geometric constructions.
9. What skills will I develop by working through Exercise 8.4?
Students will enhance their skills in drawing, measuring, and applying geometric concepts through practice.
10. Is there a specific format for the NCERT Solutions PDF?
The PDF format is user-friendly, containing organised solutions, diagrams, and clear explanations for each problem in Exercise 8.4.