Class 6 Maths Chapter 8 Questions and Answers - Free PDF Download
In NCERT Solutions Class 6 Maths Chapter 8 Exercise 8 6, you’ll get to play with lines, angles, and shapes through fun construction activities. This exercise makes tricky concepts like perpendicular bisectors and equal distances much easier by guiding you step by step. If you want a head start on what’s coming up this year, you can also check the CBSE Class 6 Maths syllabus for a quick summary.
Table of Content
Many students feel confused about how to use a compass or ruler, or how to draw accurate figures in geometry. The Vedantu NCERT Solutions offer clear methods and visuals to help you avoid mistakes and build your confidence. Practicing these solutions will not only help you understand each step but also prepare you for similar questions in exams. If you need help across the book, you can check all the NCERT Solutions for Class 6 Maths.
These solutions are also available as a free PDF download, so you can review, practice, and revise anytime you like. Use these resources to get comfortable with constructions and ace your geometry questions!
Exercise 8.6
1. Construct a bigger house in which all the sides are of length 7 cm.
Ans:
Step 1: Using a ruler, draw a line segment DE measuring 7 cm.
Step 2: Utilise a protractor to create perpendicular lines at points D and E on line DE. Mark point B on the perpendicular line at D such that BD is 7 cm long. Similarly, mark point C on the perpendicular at E, ensuring that CE is also 7 cm.
Step 3: Calculate 7 cm – 1 cm = 6 cm, and then divide by 2 to get 3 cm. Use a ruler to mark points P and Q on line DE such that DP is 3 cm and QE is 3 cm. From points P and Q, draw perpendicular lines to DE, each measuring 2 cm in length.
Step 4: Connect points R and S. With a compass set at points B and C, draw arcs with a radius of 7 cm to find their intersection point, labelled A. Then, connect points A to B and A to C. Using the compass centred at A, draw an arc from B to C. Finally, erase any unnecessary lines.
Step 5: The result is a completed drawing of the house, with all lines forming the outline measuring 7 cm.
2. Try to recreate ‘A Person’, ‘Wavy Wave’, and ‘Eyes’ from the section ‘Artworkʼ, using ideas involved in the ‘House’ construction.
Ans: A Person
Wavy Wave
Eyes
3. Is there a 4-sided figure in which all the sides are equal in length but is not a square? If such a figure exists, can you construct it?
Ans: Yes, a four-sided figure in which all sides are equal in length but is not a square does exist. This figure is called a rhombus.
Step 1: Draw a straight line and mark points A and B on it, ensuring that the distance AB measures 5 cm.
Step 2: Using a protractor, create points C and D such that the angles to the right of A and B each measure 60°.
Step 3: With a ruler, identify point P on line AC so that AC is 5 cm long, and point Q on line BD so that BD is also 5 cm. Connect points P and Q.
Step 4: Measure the distance PQ with a ruler; it should equal 5 cm. Therefore, in the figure ABQP, all sides are equal to 5 cm. Additionally, ∠A measures 60°, which is not 90°.
Hence, ABQP is not a square.
Step 5: This demonstrates that there exist four-sided figures with all sides equal in length that are not squares.
Benefits of NCERT Solutions for Class 6 Chapter 8 Playing with Constructions Exercise 8.6
This exercise Provides clear, step-by-step guidance for geometric constructions, making it easier for students to follow along.
Enhances understanding of key concepts related to angles and shapes through practical examples.
Improves confidence in using tools like compass and straightedge for precise constructions.
Encourages critical thinking and problem-solving skills as students work through construction tasks.
The solutions follow the CBSE Class 6 Maths Syllabus, which helps make sure that students are ready for their exams and understand what they need to learn.
Class 6 Maths Chapter 8: Exercises Breakdown
Important Study Material Links for Class 6 Maths Chapter 8 - Playing with Constructions
Conclusion
NCERT Solutions for Class 6 Maths Chapter 8, "Playing with Constructions," helps students understand points that are the same distance from two given points. The clear explanations make it easier to draw perpendicular bisectors and see how points are equidistant. Practising these exercises improves students' skills in geometric constructions, which are important for learning more advanced topics in geometry. With the solutions available as a FREE PDF download, students can study and review at their own pace, making learning convenient and effective.
Chapter-Specific NCERT Solutions for Class 6 Maths
The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Related Important Links for Maths Class 6
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.
FAQs on NCERT Solutions For Class 6 Maths Chapter 8 Playing With Constructions Exercise 8.6 - 2025-26
1. What is NCERT Solutions for Chapter 8 Exercise 8.6 about?
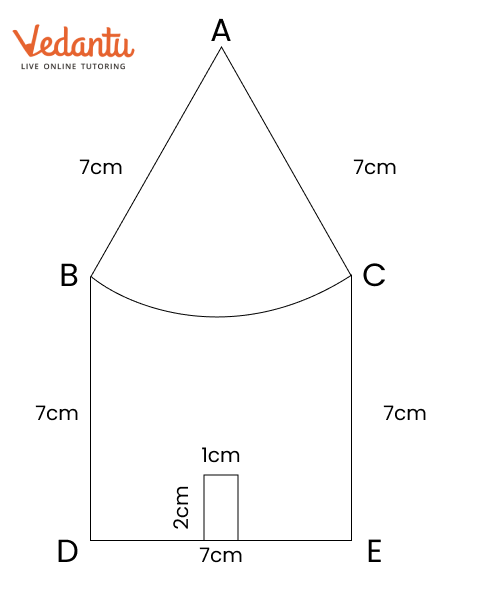
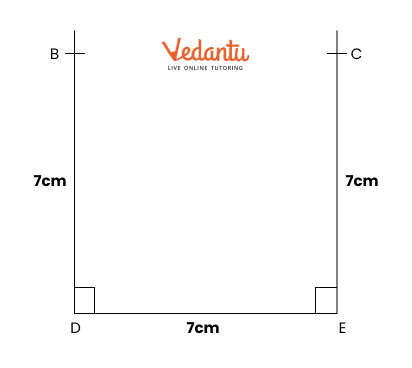
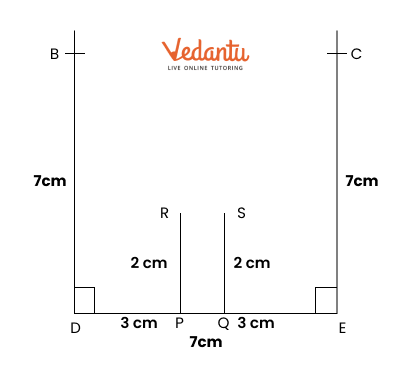
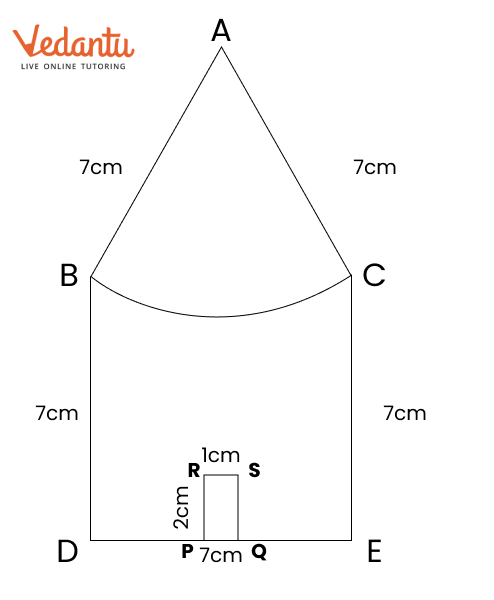
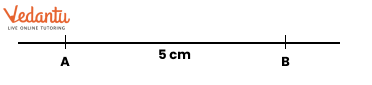
Exercise 8.6 in NCERT Solutions for Class 6 Maths focuses on finding points that are equidistant from two given points. It teaches how to construct the perpendicular bisector of a line segment. This concept helps students see how points can be the same distance from two locations.
2. Why is it important to learn about points equidistant form Chapter 8 from two given points?
Understanding equidistant points helps students learn key geometric ideas. It is useful in real-life situations, like design and measurement. This knowledge prepares students for more advanced topics in geometry.
3. What tools do I need for this NCERT Solutions for Chapter 8 exercise?
For Exercise 8.6, you need a compass, a ruler, and a pencil. The compass is used to draw arcs, while the ruler helps measure and draw straight lines. These tools are essential for making accurate geometric figures.
4. How do I construct the perpendicular bisector in NCERT Solutions for Chapter 8 Exercise 8.6?
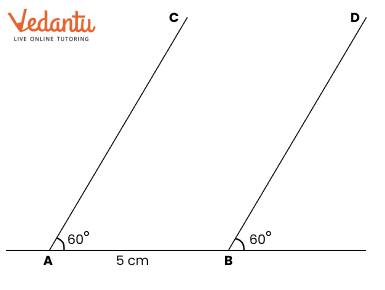
To construct the perpendicular bisector, first draw a line segment between the two points. Then, use a compass to draw arcs from each endpoint to find where they intersect. Finally, connect these points with a ruler to complete the bisector.
5. Can I see real-life examples of NCERT Solutions of equidistant points?
Yes, equidistant points can be found in everyday situations, such as in design and architecture. For example, planners often need to find points that are equally far from important locations. This helps create balanced and well-organised designs.
6. What common mistakes should I avoid when solving NCERT Solutions for Maths Class 6 Playing with Constructions?
Common mistakes include not measuring accurately or making arcs that are too small. Forgetting to mark where the arcs intersect can also lead to problems. Checking your work carefully will help ensure accuracy in your constructions.
7. How can I practise this NCERT Solutions Chapter 8 exercise 8.6 effectively?
To practise effectively, start by reviewing the steps for constructing the perpendicular bisector. Work through the problems slowly, and use NCERT Solutions to check your answers. Regular practice will help you feel more confident in your skills.
8. Are there any tips for using the compass and ruler?
Make sure the compass is tight so it doesn’t slip while drawing arcs. Keep the point steady to create accurate curves. Line up the ruler correctly with the points before drawing straight lines for better results.
9. What should I do if I don’t understand a step?
If you don’t understand a step, review the explanations in the NCERT Solutions. You can also refer to revision notes and important questions for help. Practising the step a few more times can make things clearer.
10. How can this Chapte r8 Exercise 8.6 help in future studies?
This exercise teaches important skills in geometry that are needed for later topics. Understanding equidistance helps students with more advanced concepts. It also improves problem-solving skills that are useful in other subjects.
11. Can I use this NX=CERT Solutions exercise in my projects?
Yes, the ideas from Exercise 8.6 can be useful in various projects, especially in design and architecture. Knowing how to find equidistant points can help you create balanced designs. This knowledge can enhance the quality of your project work.
12. How do I download the NCERT Solutions PDF?
To download the NCERT Solutions for Class 6 Maths PDF, visit the official NCERT website. Look for the section on Class 6 Maths and find Chapter 8. You should see an option to download the solutions as a PDF file.
13. What are the key takeaways from this NCERT Solutions Chapter 8 Exercise 8.6?
Key takeaways include understanding equidistance and how to construct perpendicular bisectors. Students learn to use geometric tools correctly and develop important problem-solving skills. This exercise connects geometry to real-life situations, making it more interesting.
