NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals

Exercise 2.1: Multiplication of Fractions

• Multiplying Fractions by Whole Numbers: Understanding how to multiply fractions by whole numbers.

• Multiplying Two Fractions: Learning the method to multiply two fractions.

• Multiplying Mixed Numbers: Converting mixed numbers to improper fractions and then multiplying them.

Exercise 2.2: Division of Fractions

• Reciprocal of a Fraction: Introduction to the concept of reciprocals.

• Dividing Fractions by Whole Numbers: Method to divide fractions by whole numbers using reciprocals.

• Dividing a Fraction by Another Fraction: Understanding the steps to divide one fraction by another fraction.

• Word Problems: Applying division of fractions to solve real-life problems.

Exercise 2.3: Multiplication of Decimal Numbers

This section in Maths Class 7 Chapter 2 covers the rules and methods for multiplying decimal numbers. It includes step-by-step instructions for aligning the decimal points and performing multiplication, followed by placing the decimal point in the product correctly. Practical examples and problems help reinforce the concept and provide practice in multiplying decimals in various contexts.

Exercise 2.4: Division of Decimal Numbers

This section focuses on dividing decimal numbers, explaining how to handle the decimal point in both the dividend and the divisor. It includes methods for converting the divisor into a whole number by multiplying both the dividend and the divisor by a power of ten. The section in Class 7 Fractions and Decimals provides numerous examples and exercises to practice the division of decimals, ensuring a clear understanding of the process.

Access NCERT Solutions for Class 7 Maths Chapter 2 – Fractions and Decimals

Exercise - 2.1

1. Which of the drawings $(a)\,to\,(d)$ show:

(i). $\text{2 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{5}}$

(a) 

Ans: corresponds to $\text{(d)}$  

Because,  $2\times \frac{1}{5}=\frac{1}{5}+\frac{1}{5}$                                                                

(ii). $\text{2 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{2}}$

(b)

Ans: corresponds to $\text{(b)}$

Because, $2\times \frac{1}{2}=\frac{1}{2}+\frac{1}{2}$

(iii). $\text{3 }\!\!\times\!\!\text{ }\frac{\text{2}}{\text{3}}$

(c)

Ans:  corresponds to $\text{(a)}$   

Because, $3\times \frac{2}{3}=\frac{2}{3}+\frac{2}{3}+\frac{2}{3}$ 

(iv). $\text{3 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{4}}$

(d)

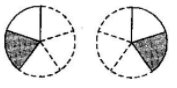
Ans: Corresponds to $\text{(c)}$

Because, $3\times \frac{1}{4}=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$ 

2. Some pictures $\left( \text{a} \right)\,\text{to}\,\left( \text{c} \right)$ are given below. Tell which of them show: 

(i). $\text{3 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{5}}\text{=}\frac{\text{3}}{\text{5}}$

(a)

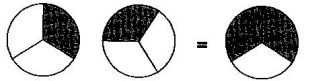
Ans: Corresponds to $\text{(c)}$                    

Because, $3\times \frac{1}{5}=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}$  

(ii). $\text{2 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{3}}\text{=}\frac{\text{2}}{\text{3}}$ 

(b)

Ans: Corresponds to $\text{(a)}$                   

Because, $2\times \frac{1}{3}=\frac{1}{3}+\frac{1}{3}$ 

(iii). $\text{3 }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{4}}\text{=2}\frac{\text{1}}{\text{4}}$

(c)

Ans: Corresponds to $\text{(b)}$                  

Because, $3\times \frac{3}{4}=\frac{3}{4}+\frac{3}{4}+\frac{3}{4}$      

3. Multiply and reduce to lowest form and convert into a mixed fraction:

(i). $\text{7 }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{5}}$        

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,   

$7\times \frac{3}{5}=\frac{7\times 3}{5}=\frac{21}{5}=4\frac{1}{5}$

(ii). $\text{4 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{3}}$ 

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$4\times \frac{1}{3}=\frac{4\times 1}{3}=\frac{4}{3}=1\frac{1}{3}$ 

(iii). $\text{2 }\!\!\times\!\!\text{ }\frac{\text{6}}{\text{7}}$    

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$2\times \frac{6}{7}=\frac{2\times 6}{7}=\frac{12}{7}=1\frac{5}{7}$       

(iv). $\text{5 }\!\!\times\!\!\text{ }\frac{\text{2}}{\text{9}}$ 

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$5\times \frac{2}{9}=\frac{5\times 2}{9}=\frac{10}{9}=1\frac{1}{9}$

(v). $\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 4}$     

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$\frac{2}{3}\times 4=\frac{2\times 4}{3}=\frac{8}{3}=2\frac{2}{3}$   

(vi)  $\frac{\text{5}}{\text{2}}\text{ }\!\!\times\!\!\text{ 6}$    

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$\frac{5}{2}\times 6=5\times 3=15$

(vii)   $\text{11 }\!\!\times\!\!\text{ }\frac{\text{4}}{\text{7}}$    

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$11\times \frac{4}{7}=\frac{11\times 4}{7}=\frac{44}{7}=6\frac{2}{7}$ 

(viii)  $\text{20 }\!\!\times\!\!\text{ }\frac{\text{4}}{\text{5}}$ 

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,

$20\times \frac{4}{5}=4\times 4=16$

(ix)  $\text{13 }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{3}}$      

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,    

$13\times \frac{1}{3}=\frac{13\times 1}{3}=\frac{13}{3}=4\frac{1}{3}$ 

(x)  $\text{15 }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{5}}$ 

Ans: Multiplying and reducing to lowest form and converting into a mixed fraction,   

$15\times \frac{3}{5}=3\times 3=9$                

4. Shade: 

(i). $\frac{\text{1}}{\text{2}}$ of the circles in box

(ii).

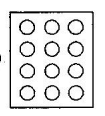
Ans: Half of the circles in the box are,

$\frac{\text{1}}{\text{2}}\,\text{of}\,\text{12}\,\text{circles=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ 12=6}\,\text{circles}$

(iii). $\frac{\text{2}}{\text{3}}$ of the triangles in box 

(b)

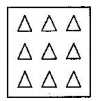
Ans: Two-third of the triangles in the box are,$\frac{\text{2}}{\text{3}}\,\text{of}\,\text{9}\,\text{triangles=}\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 9=2 }\!\!\times\!\!\text{ 3=6}\,\text{triangles}$

(iv). $\frac{\text{3}}{\text{5}}$ of the squares inbox

(v). (c)

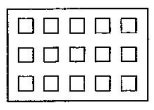
Ans: Three-fifth of the squares in the box are,

$\frac{\text{3}}{\text{5}}\,\text{of}\,\text{15}\,\text{squares=}\frac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ 15=3 }\!\!\times\!\!\text{ 3=9}\,\text{squares}$

5. Find

(a).$\frac{\text{1}}{\text{2}}\,\text{of}\,\text{(i)}\,\text{24}\,\text{(ii)}\,\text{46}$

Ans:

(i) Calculating the value,

$\frac{\text{1}}{\text{2}}\,\text{of}\,\text{24=12}$

(ii) Calculating the value,

$\frac{\text{1}}{\text{2}}\,\text{of}\,\text{46=23}$ 

(b). $\frac{\text{2}}{\text{3}}\,\text{of}\,\text{(i)}\,\text{18}\,\text{(ii)}\,\text{27}$ 

Ans:

(i) Calculating the value, $\frac{\text{2}}{\text{3}}\,\text{of}\,\text{18=}\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 18=2 }\!\!\times\!\!\text{ 6=12}$

(ii) Calculating the value, $\frac{\text{2}}{\text{3}}\,\text{of}\,\text{27=}\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 27=2 }\!\!\times\!\!\text{ 9=18}$ 

(c)  $\frac{\text{3}}{\text{4}}\,\text{of}\,\text{(i)}\,\text{16}\,\text{(ii)}\,\text{36}$          

Ans:

(i) Calculating the value,

$\frac{\text{3}}{\text{4}}\,\text{of}\,\text{16=}\frac{\text{3}}{\text{4}}\text{ }\!\!\times\!\!\text{ 16=3 }\!\!\times\!\!\text{ 4=12}$

(ii) Calculating the value,

$\frac{\text{3}}{\text{4}}\,\text{of}\,36\text{=}\frac{\text{3}}{\text{4}}\text{ }\!\!\times\!\!\text{ 36=3 }\!\!\times\!\!\text{ 9=27}$  

(d)  $\frac{\text{4}}{\text{5}}\,\text{of}\,\text{(i)}\,\text{20}\,\text{(ii)}\,\text{35}$ 

Ans:

(i) Calculating the value,

$\frac{\text{4}}{\text{5}}\,\text{of}\,20\text{=}\frac{\text{4}}{\text{5}}\text{ }\!\!\times\!\!\text{ 20=4 }\!\!\times\!\!\text{ 4=16}$

(ii) Calculating the value,

$\frac{\text{4}}{\text{5}}\,\text{of}\,35\text{=}\frac{\text{4}}{\text{5}}\text{ }\!\!\times\!\!\text{ 35=4 }\!\!\times\!\!\text{ 7=28}$ 

6.   Multiply and express as a mixed fraction:

(a)  $\text{3 }\!\!\times\!\!\text{ 5}\frac{\text{1}}{\text{5}}$       

Ans: Multiplying and expressing the term as mixed fraction,

$3\times 5\frac{1}{5}=3\times \frac{26}{5}=\frac{3\times 26}{5}=\frac{78}{5}=15\frac{3}{5}$

(b) $\text{5 }\!\!\times\!\!\text{ 6}\frac{\text{3}}{\text{4}}$          

Ans: Multiplying and expressing the term as mixed fraction,

$5\times 6\frac{3}{4}=5\times \frac{27}{4}=\frac{5\times 27}{4}=\frac{135}{4}=33\frac{3}{4}$ 

(c) $\text{7 }\!\!\times\!\!\text{ 2}\frac{\text{1}}{\text{4}}$

Ans: Multiplying and expressing the term as mixed fraction,

$7\times 2\frac{1}{4}=7\times \frac{9}{4}=\frac{7\times 9}{4}=\frac{63}{4}=15\frac{3}{4}$        

(d)  $\text{4 }\!\!\times\!\!\text{ 6}\frac{\text{1}}{\text{3}}$ 

Ans: Multiplying and expressing the term as mixed fraction,

$4\times 6\frac{1}{3}=4\times \frac{19}{3}=\frac{4\times 19}{3}=\frac{76}{3}=25\frac{1}{3}$ 

(e)  $\text{3}\frac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ 6}$ 

Ans: Multiplying and expressing the term as mixed fraction,

$3\frac{1}{4}\times 6=\frac{13}{4}\times 6=\frac{13\times 3}{2}=\frac{39}{2}=19\frac{1}{2}$  

(f)  $\text{3}\frac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ 8}$ 

Ans: Multiplying and expressing the term as mixed fraction,

$3\frac{2}{5}\times 8=\frac{17}{5}\times 8=\frac{17\times 8}{5}=\frac{136}{5}=27\frac{1}{5}$

7. Find:

(a)  $\frac{\text{1}}{\text{2}}\,\text{of}\,\text{(i)}\,\text{2}\frac{\text{3}}{\text{4}}\,\text{(ii)}\,\text{4}\frac{\text{2}}{\text{9}}$             

Ans:

(i) Calculating the value, \[\frac{\text{1}}{\text{2}}\,\text{of}\,\text{2}\frac{\text{3}}{\text{4}}\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ 2}\frac{\text{3}}{\text{4}}\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\frac{\text{11}}{\text{4}}\text{=}\frac{\text{11}}{\text{8}}\text{=1}\frac{\text{3}}{\text{8}}\] 

(ii) Calculating the value, \[\frac{\text{1}}{\text{2}}\,\text{of}\,\text{4}\frac{\text{2}}{\text{9}}\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ 4}\frac{\text{2}}{\text{9}}\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\frac{\text{38}}{\text{9}}\text{=}\frac{\text{19}}{\text{9}}\text{=2}\frac{\text{1}}{\text{9}}\] 

(b)  $\frac{\text{5}}{\text{8}}\,\text{of}\,\text{(i)}\,\text{3}\frac{\text{5}}{\text{6}}\,\text{(ii)}\,\text{9}\frac{\text{2}}{\text{3}}$ 

Ans:

(i) Calculating the value, \[\frac{\text{5}}{\text{8}}\,\text{of}\,\text{3}\frac{\text{5}}{\text{6}}\text{=}\frac{\text{5}}{\text{8}}\text{ }\!\!\times\!\!\text{ 3}\frac{\text{5}}{\text{6}}\text{=}\frac{\text{5}}{\text{8}}\text{ }\!\!\times\!\!\text{ }\frac{\text{23}}{\text{6}}\text{=}\frac{\text{115}}{\text{48}}\text{=2}\frac{\text{19}}{\text{48}}\] 

(ii) Calculating the value, \[\frac{\text{5}}{\text{8}}\,\text{of}\,\text{9}\frac{\text{2}}{\text{3}}\text{=}\frac{\text{5}}{\text{8}}\text{ }\!\!\times\!\!\text{ 9}\frac{\text{2}}{\text{3}}\text{=}\frac{\text{5}}{\text{8}}\text{ }\!\!\times\!\!\text{ }\frac{\text{29}}{\text{3}}\text{=}\frac{\text{145}}{\text{24}}\text{=6}\frac{\text{1}}{\text{24}}\] 

8.  Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained $\text{5}$ liters of water. Vidya consumed $\frac{\text{2}}{\text{5}}$ of the water. Pratap consumed the remaining water.

(i). How much water did Vidya drink?

Ans:   Water consumed by Vidya is,$\text{=}\frac{\text{2}}{\text{5}}\,\text{of}\,\text{5}\,\text{litres=}\frac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ 5=2}\,\text{litres}$ 

Hence, Vidya drank $2$ litres of water from the bottle.

(ii). What fraction of the total quantity of water did Pratap drink?

Ans: Water consumed by Pratap \[\text{= }\left( \text{1-}\frac{\text{2}}{\text{5}} \right)\text{  }\]part of bottle

Pratap consumed $\frac{\text{3}}{\text{5}}\,\text{of}\,\text{5}\,\text{litres}\,\text{water=}\frac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ 5=3}\,\text{lites}$ 

Hence, Pratap drank $\frac{3}{5}$ part of the total quantity of water present in the bottle.

Exercise - 2.2

1. Find:

(i) $\frac{\text{1}}{\text{4}}\,\text{of}$ (a) $\frac{\text{1}}{\text{4}}$ (b) $\frac{\text{3}}{\text{5}}$ (c) $\frac{\text{4}}{\text{3}}$ 

Ans:

(a) Calculating the value,

$\frac{\text{1}}{\text{4}}\,\text{of}\,\frac{\text{1}}{\text{4}}\text{=}\frac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ }\frac{\text{1}}{\text{4}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ 1}}{\text{4 }\!\!\times\!\!\text{ 4}}\text{=}\frac{\text{1}}{\text{16}}$ 

(b) Calculating the value,

$\frac{\text{1}}{\text{4}}\,\text{of}\,\frac{\text{3}}{\text{5}}\text{=}\frac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{4}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ 3}}{\text{4 }\!\!\times\!\!\text{ 4}}\text{=}\frac{\text{3}}{\text{16}}$ 

(c) Calculating the value,

$\frac{\text{1}}{\text{4}}\,\text{of}\,\frac{\text{4}}{\text{3}}\text{=}\frac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ }\frac{\text{4}}{\text{3}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ 4}}{\text{4 }\!\!\times\!\!\text{ 3}}\text{=}\frac{\text{1}}{\text{3}}$ 

(ii) \[\frac{\text{1}}{\text{7}}\,\text{of}\] (a) \[\frac{\text{2}}{\text{9}}\] (b) \[\frac{\text{6}}{\text{5}}\] (c) $\frac{\text{3}}{\text{10}}$ 

Ans:

(a) Calculating the value,

$\frac{\text{1}}{\text{7}}\,\text{of}\,\frac{\text{2}}{\text{9}}\text{=}\frac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\frac{\text{2}}{\text{9}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ 2}}{\text{7 }\!\!\times\!\!\text{ 9}}\text{=}\frac{\text{2}}{\text{63}}$ 

(b) Calculating the value,

$\frac{\text{1}}{\text{7}}\,\text{of}\,\frac{\text{2}}{\text{9}}\text{=}\frac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\frac{\text{6}}{\text{5}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ 6}}{\text{7 }\!\!\times\!\!\text{ 5}}\text{=}\frac{\text{6}}{\text{35}}$ 

(c) Calculating the value,

$\frac{\text{1}}{\text{7}}\,\text{of}\,\frac{\text{2}}{\text{9}}\text{=}\frac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{10}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ 3}}{\text{7 }\!\!\times\!\!\text{ 10}}\text{=}\frac{3}{70}$ 

2. Multiply and reduce to lowest form (if possible):

(i) $\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 2}\frac{\text{2}}{\text{3}}$ 

Ans: Multiplying and reducing to lowest form,  

$\frac{2}{3}\times 2\frac{2}{3}=\frac{2}{3}\times \frac{8}{3}=\frac{2\times 8}{3\times 3}=\frac{16}{9}=1\frac{7}{9}$ 

(ii) $\frac{\text{2}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\frac{\text{7}}{\text{9}}$

Ans: Multiplying and reducing to lowest form,  

$\frac{2}{7}\times \frac{7}{9}=\frac{2\times 7}{7\times 9}=\frac{2}{9}$

(iii) $\frac{\text{3}}{\text{8}}\text{ }\!\!\times\!\!\text{ }\frac{\text{6}}{\text{4}}$ 

Ans: Multiplying and reducing to lowest form, 

$\frac{3}{8}\times \frac{6}{4}=\frac{3\times 6}{8\times 4}=\frac{3\times 3}{8\times 2}=\frac{9}{16}$

(iv) $\frac{\text{9}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{5}}$ 

Ans: Multiplying and reducing to lowest form, 

$\frac{9}{5}\times \frac{3}{5}=\frac{9\times 3}{5\times 5}=\frac{27}{25}=1\frac{2}{25}$

(v) $\frac{\text{1}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\frac{\text{15}}{\text{8}}$ 

Ans: Multiplying and reducing to lowest form,

$\frac{1}{3}\times \frac{15}{8}=\frac{1\times 15}{3\times 8}=\frac{1\times 5}{1\times 8}=\frac{5}{8}$

(vi) $\frac{\text{11}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{10}}$ 

Ans: Multiplying and reducing to lowest form,  

$\frac{11}{2}\times \frac{3}{10}=\frac{11\times 3}{2\times 10}=\frac{33}{20}=1\frac{3}{20}$ 

(vii) $\frac{\text{4}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\frac{\text{12}}{\text{7}}$ 

Ans: Multiplying and reducing to lowest form,  

$\frac{4}{5}\times \frac{12}{7}=\frac{4\times 12}{5\times 7}=\frac{48}{35}=1\frac{13}{35}$

3. Multiply the following fractions:

(i) $\frac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ 5}\frac{\text{1}}{\text{4}}$

Ans: Performing multiplication,

$\frac{2}{5}\times 5\frac{1}{4}=\frac{2}{5}\times \frac{21}{4}=\frac{2\times 21}{5\times 4}=\frac{1\times 21}{5\times 2}=\frac{21}{10}=2\frac{1}{10}$ 

(ii) $\text{6}\frac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\frac{\text{7}}{\text{9}}$ 

Ans: Performing multiplication,

$6\frac{2}{5}\times \frac{7}{9}=\frac{32}{5}\times \frac{7}{9}=\frac{32\times 7}{5\times 9}=\frac{224}{45}=4\frac{44}{45}$

(iii) $\frac{\text{3}}{\text{2}}\text{ }\!\!\times\!\!\text{ 5}\frac{\text{1}}{\text{3}}$ 

Ans: Performing multiplication,

$\frac{3}{2}\times 5\frac{1}{3}=\frac{3}{2}\times \frac{16}{3}=\frac{48}{6}=8$ 

(iv) $\frac{\text{5}}{\text{6}}\text{ }\!\!\times\!\!\text{ 2}\frac{\text{3}}{\text{7}}$ 

Ans: Performing multiplication,

$\frac{5}{6}\times 2\frac{3}{7}=\frac{5}{6}\times \frac{17}{7}=\frac{85}{42}=2\frac{1}{42}$ 

(v) $\text{3}\frac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\frac{\text{4}}{\text{7}}$

Ans: Performing multiplication,

$3\frac{2}{5}\times \frac{4}{7}=\frac{17}{7}\times \frac{4}{7}=\frac{68}{35}=1\frac{33}{35}$

(vi) $\text{2}\frac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ 3}$ 

Ans: Performing multiplication,

$2\frac{3}{5}\times 3=\frac{13}{5}\times \frac{3}{1}=\frac{13\times 3}{5\times 1}=\frac{39}{5}=7\frac{4}{5}$

(vii) $\text{3}\frac{\text{4}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{5}}$ 

Ans: Performing multiplication,

$3\frac{4}{7}\times \frac{3}{5}=\frac{25}{7}\times \frac{3}{5}=\frac{5\times 3}{7\times 1}=\frac{15}{7}=2\frac{1}{7}$

4. Which is greater:

(i) $\frac{\text{2}}{\text{7}}\,\text{of}\,\frac{\text{3}}{\text{4}}\,\text{or}\,\frac{\text{3}}{\text{5}}\,\text{of}\,\frac{\text{5}}{\text{8}}$

Ans: Calculating the greater term,

$\frac{\text{2}}{\text{7}}\,\text{of}\,\frac{\text{3}}{\text{4}}\,\text{or}\,\frac{\text{3}}{\text{5}}\,\text{of}\,\frac{\text{5}}{\text{8}}$                

$\Rightarrow \frac{\text{2}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{4}}\,\text{or}\,\frac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\frac{\text{5}}{\text{8}}$ 

$\Rightarrow \frac{\text{3}}{\text{14}}\,\text{or}\,\frac{\text{3}}{\text{8}}$

$\Rightarrow \frac{3}{14}<\frac{3}{8}$ 

Hence, $\frac{\text{3}}{\text{5}}\,\text{of}\,\frac{\text{5}}{\text{8}}$ is greater.

(ii) $\frac{\text{1}}{\text{2}}\,\text{of}\,\frac{\text{6}}{\text{7}}\,\text{or}\,\frac{\text{2}}{\text{3}}\,\text{of}\,\frac{\text{3}}{\text{7}}$ 

Ans:

Calculating the greater term,

$\frac{\text{1}}{\text{2}}\,\text{of}\,\frac{\text{6}}{\text{7}}\,\text{or}\,\frac{\text{2}}{\text{3}}\,\text{of}\,\frac{\text{3}}{\text{7}}$                

$\Rightarrow \frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\frac{\text{6}}{\text{7}}\,\text{or}\,\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{7}}$ 

$\Rightarrow \frac{\text{6}}{\text{14}}\,\text{or}\,\frac{\text{2}}{\text{7}}$ $\Rightarrow \frac{\text{6}}{\text{14}}>\frac{\text{2}}{\text{7}}$ 

Hence, $\frac{\text{1}}{\text{2}}\,\text{of}\,\frac{\text{6}}{\text{7}}$ is greater.

5. Saili plants \[\text{4}\] saplings in a row in her garden. The distance between

two adjacent saplings is \[\frac{\text{3}}{\text{4}}\] m. Find the 

distance between the first and the last sapling. 

Ans: Given: Saili plants \[4\] saplings in a row where the distance between two 

adjacent saplings $=\frac{3}{4}$m.

The number of gaps in saplings \[=\text{ }3\] 

Hence, 

The distance between the first and the last saplings$\text{=3 }\!\!\times\!\!\text{ }\frac{\text{3}}{\text{4}}\text{=}\frac{\text{9}}{\text{4}}\text{m=2}\frac{\text{1}}{\text{4}}\text{m}$

Therefore, the distance between the first and the last saplings is $\text{2}\frac{\text{1}}{\text{4}}\,\text{m}$

6. Lipika reads a book for $\text{1}\frac{\text{3}}{\text{4}}$ hours every day. 

She reads the entire book in \[\text{6}\] days. How many hours in all were 

required by her to read the book?

Ans: Given: Time taken for reading a book by Lipika $=1\frac{3}{4}$ hours.

Lipika reads the entire book in $6$ days

Calculating the Total hours taken by Lipika to read the entire book,

$=1\frac{3}{4}\times 6=\frac{7}{4}\times 6=\frac{21}{2}=10\frac{1}{2}$ hours.

Hence, it would take $10$ hours to read the book.

7. A car runs $\text{16}$ km using \[\text{1}\] litre of petrol. How much 

distance will it cover using   $\text{2}\frac{\text{3}}{\text{4}}$ litres of 

petrol?

Ans: Given: A car covers the distance$\text{=16}\,\text{km}$ in $1$ litre of 

petrol.

Calculating the distance covered by car in $2\frac{3}{4}$ litres of petrol,

Distance$\text{=2}\frac{\text{3}}{\text{4}}\,\text{of}\,\text{16}\,\text{km=}\frac{\text{11}}{\text{4}}\text{ }\!\!\times\!\!\text{ 16=44}\,\text{km}$

Therefore, car will cover a distance of $44$ km in $2\frac{3}{4}$ litres of petrol.

8. (a)

(i) Provide the number in the box , such that 

$\frac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\text{=}\frac{\text{10}}{\text{30}}$ 

Ans: The number inside the box should be $\frac{2}{3}\times =\frac{10}{30}$ 

(ii) The simplest form of the number obtained in $$ is _____.

Ans: The simplest form of the number obtained in 

$\frac{\text{5}}{\text{10}}\,\text{is}\,\frac{\text{1}}{\text{2}}$

(b) 

(i) Provide the number in the box $$ , such that $\frac{3}{5}\times =\frac{24}{75}$.

Ans: The number inside the box should be $\frac{3}{5}\times =\frac{24}{75}$ 

(ii) The simplest form of the number obtained in is______.

Ans: The simplest form of the number obtained in 

$\frac{\text{8}}{\text{15}}\,\text{is}\,\frac{\text{8}}{\text{15}}$

Exercise - 2.3

1. Find:

(i) $\text{12 }\!\!\div\!\!\text{ }\frac{\text{3}}{\text{4}}$ 

Ans: Calculating the value,

$12\div \frac{3}{4}=12\times \frac{4}{3}=16$

(ii) $\text{14 }\!\!\div\!\!\text{ }\frac{\text{5}}{\text{6}}$ 

Ans: Calculating the value,

$14\div \frac{5}{6}=14\times \frac{6}{5}=\frac{84}{5}=16\frac{4}{5}$ 

(iii) $\text{8 }\!\!\div\!\!\text{ }\frac{\text{7}}{\text{3}}$ 

Ans:  Calculating the value,

$8\div \frac{7}{3}=8\times \frac{3}{7}=\frac{24}{7}=3\frac{3}{7}$

(iv) $\text{4 }\!\!\div\!\!\text{ }\frac{\text{8}}{\text{3}}$ 

Ans: Calculating the value,

$4\div \frac{8}{3}=4\times \frac{3}{8}=\frac{3}{2}=1\frac{1}{2}$

(v) $\text{3 }\!\!\div\!\!\text{ 2}\frac{\text{1}}{\text{3}}$ 

Ans: Calculating the value,

$3\div 2\frac{1}{3}=3\div \frac{7}{3}=3\times \frac{3}{7}=\frac{9}{7}=1\frac{2}{7}$           

(vi) \[\text{5 }\!\!\div\!\!\text{ 3}\frac{\text{4}}{\text{7}}\] 

Ans: Calculating the value,

$5\div 3\frac{4}{7}=5\div \frac{25}{7}=5\times \frac{7}{25}=\frac{7}{5}=1\frac{2}{5}$

2. Find the reciprocal of each of the following fractions. Classify the 

reciprocals as proper fraction, improper fractions and whole numbers.

(i) $\frac{\text{3}}{\text{7}}$

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of $\frac{\text{3}}{\text{7}}\text{=}\frac{\text{7}}{\text{3}}\to \text{Improper}\,\text{fraction}$  

(ii) $\frac{\text{5}}{\text{8}}$

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of$\frac{\text{5}}{\text{8}}\text{=}\frac{\text{8}}{\text{5}}\to \text{Improper}\,\text{fraction}$

(iii) $\frac{\text{9}}{\text{7}}$

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of $\frac{\text{9}}{\text{7}}\text{=}\frac{\text{7}}{\text{9}}\to \text{Proper}\,\text{fraction}$

(iv) $\frac{\text{6}}{\text{5}}$ 

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of $\frac{\text{6}}{\text{5}}\text{=}\frac{\text{5}}{\text{6}}\to \text{Proper}\,\text{fraction}$

(v) $\frac{\text{12}}{\text{7}}$ 

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of $\frac{\text{12}}{\text{7}}\text{=}\frac{\text{7}}{\text{12}}\to \text{Proper}\,\text{fraction}$  

(vi) $\frac{\text{1}}{\text{8}}$

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of $\frac{\text{9}}{\text{7}}\text{=8}\to \text{Whole number}$

(vii) $\frac{\text{1}}{\text{11}}$ 

Ans: Calculating the reciprocal and stating the type of the fraction,

Reciprocal of $\frac{\text{1}}{\text{11}}\text{=11}\to \text{Whole number}$

3. Find:

(i) $\frac{\text{7}}{\text{3}}\text{ }\!\!\div\!\!\text{ 2}$ 

Ans: Calculating the value,

$\frac{7}{3}\div 2=\frac{7}{3}\times \frac{1}{2}=\frac{7\times 1}{3\times 2}=\frac{7}{6}=1\frac{1}{6}$

(ii) $\frac{\text{4}}{\text{9}}\text{ }\!\!\div\!\!\text{ 5}$

Ans: Calculating the value,

$\frac{4}{9}\div 5=\frac{4}{9}\times \frac{1}{5}=\frac{4\times 1}{9\times 5}=\frac{4}{45}$ 

(iii) $\frac{\text{6}}{\text{13}}\text{ }\!\!\div\!\!\text{ 7}$ 

Ans: Calculating the value,

$\frac{6}{13}\div 7=\frac{6}{13}\times \frac{1}{7}=\frac{6\times 1}{13\times 7}=\frac{6}{91}$ 

(iv) $\text{4}\frac{\text{1}}{\text{3}}\text{ }\!\!\div\!\!\text{ 3}$

Ans:  Calculating the value,

$4\frac{1}{3}\div 3=\frac{13}{3}\div 3=\frac{13}{3}\times \frac{1}{3}=\frac{13}{9}=1\frac{4}{9}$

(v) $\text{3}\frac{\text{1}}{\text{2}}\text{ }\!\!\div\!\!\text{ 4}$ 

Ans: Calculating the value,

$3\frac{1}{2}\div 4=\frac{7}{2}\div 4=\frac{7}{2}\times \frac{1}{4}=\frac{7}{8}$

(vi) $\text{4}\frac{\text{3}}{\text{7}}\text{ }\!\!\div\!\!\text{ 7}$ 

Ans: Calculating the value,

$4\frac{3}{7}\div 7=\frac{31}{7}\div 7=\frac{31}{7}\times \frac{1}{7}=\frac{31}{49}$

4. Find:

(i) $\frac{\text{2}}{\text{5}}\text{ }\!\!\div\!\!\text{ }\frac{\text{1}}{\text{2}}$

Ans:  Calculating the value,

$\frac{2}{5}\div \frac{1}{2}=\frac{2}{5}\times \frac{2}{1}=\frac{2\times 2}{5\times 1}=\frac{4}{5}$ 

(ii) $\frac{\text{4}}{\text{9}}\text{ }\!\!\div\!\!\text{ }\frac{\text{2}}{\text{3}}$ 

Ans: Calculating the value,

$\frac{4}{9}\div \frac{2}{3}=\frac{4}{9}\times \frac{3}{2}=\frac{2}{3}$

(iii) $\frac{\text{3}}{\text{7}}\text{ }\!\!\div\!\!\text{ }\frac{\text{8}}{\text{7}}$

Ans:  Calculating the value,

$\frac{3}{7}\div \frac{8}{7}=\frac{3}{7}\times \frac{7}{8}=\frac{3}{8}$

(iv) $\text{2}\frac{\text{1}}{\text{3}}\text{ }\!\!\div\!\!\text{ }\frac{\text{3}}{\text{5}}$ 

Ans: Calculating the value,

$2\frac{1}{3}\div \frac{3}{5}=\frac{7}{3}\div \frac{3}{5}=\frac{7}{3}\times \frac{5}{3}=\frac{35}{9}=3\frac{8}{9}$

(v) $\text{3}\frac{\text{1}}{\text{2}}\text{ }\!\!\div\!\!\text{ }\frac{\text{8}}{\text{3}}$ 

Ans: Calculating the value,

$3\frac{1}{2}\div \frac{8}{3}=\frac{7}{2}\div \frac{3}{8}=\frac{7}{2}\times \frac{3}{8}=\frac{7\times 3}{2\times 8}=\frac{21}{16}=1\frac{5}{16}$

(vi) $\frac{\text{2}}{\text{5}}\text{ }\!\!\div\!\!\text{ 1}\frac{\text{1}}{\text{2}}$

Ans: Calculating the value,

$2\frac{1}{3}\div \frac{3}{5}=\frac{2}{5}\div 1\frac{1}{2}=\frac{2}{5}\div \frac{3}{2}=\frac{2}{5}\times \frac{2}{3}=\frac{2\times 2}{5\times 3}=\frac{4}{15}$

(vii) $\text{3}\frac{\text{1}}{\text{5}}\text{ }\!\!\div\!\!\text{ 1}\frac{\text{2}}{\text{3}}$

Ans:  Calculating the value,

$3\frac{1}{5}\div 1\frac{2}{3}=\frac{16}{5}\div \frac{5}{3}=\frac{16}{5}\times \frac{3}{5}=\frac{16\times 3}{5\times 5}=\frac{48}{25}=1\frac{23}{25}$

(viii) $\text{2}\frac{\text{1}}{\text{5}}\text{ }\!\!\div\!\!\text{ 1}\frac{\text{1}}{\text{5}}$ 

Ans: Calculating the value,

$2\frac{1}{5}\div 1\frac{1}{5}=\frac{11}{5}\div \frac{6}{5}=\frac{11}{5}\times \frac{5}{6}=\frac{11}{6}=1\frac{5}{6}$

Exercise 2.4

1. Find:

(i) $\text{0}\text{.2 }\!\!\times\!\!\text{ 6}$ 

Ans: Calculating the value,

\[0.2\times 6=1.2\]

(ii) $\text{8 }\!\!\times\!\!\text{ 4}\text{.6}$

Ans:  Calculating the value,

\[8\times 4.6=36.8\]

(iii) $\text{2}\text{.71 }\!\!\times\!\!\text{ 5}$ 

Ans: Calculating the value,

\[2.71\times 5=13.55\]

(iv) $\text{20}\text{.1 }\!\!\times\!\!\text{ 4}$ 

Ans: Calculating the value,

\[20.1\times 4=80.4\]

(v) $\text{0}\text{.05 }\!\!\times\!\!\text{ 7}$ 

Ans: Calculating the value,

\[0.05\times 7=0.35\]

(vi) $\text{211}\text{.02 }\!\!\times\!\!\text{ 4}$ 

Ans: Calculating the value,

\[211.02\times 4=844.08\]

(vii) $\text{2 }\!\!\times\!\!\text{ 0}\text{.86}$ 

Ans: Calculating the value,

\[2\times 0.86=1.72\]

2. Find the area of rectangle whose length is \[\text{5}\text{.7 cm}\] and 

breadth is \[\text{3 cm}\text{.}\]

Ans: Given: The \[\text{Length of rectangle = 5}\text{.7 cm and Breadth of 

rectangle = 3 cm}\] 

Applying the area of rectangle formula,

\[\text{Area of rectangle = Length x Breadth}\] 

\[\text{= 5}\text{.7 x 3 = 17}\text{.1 c}{{\text{m}}^{2}}\]  

Hence, the area of rectangle is $\text{17}\text{.1}\,\text{c}{{\text{m}}^{\text{2}}}$.

3. Find:

(i) \[\text{1}\text{.3 }\!\!\times\!\!\text{ 10}\] 

Ans: Calculating the value,

$1.3\times 10=13.0$

(ii) \[\text{36}\text{.8 }\!\!\times\!\!\text{ 10}\] 

Ans: Calculating the value,

$36.8\times 10=368.0$

(iii) \[\text{153}\text{.7 }\!\!\times\!\!\text{ 10}\] 

Ans: Calculating the value,

$153.7\times 10=1537.0$

(iv) \[\text{168}\text{.07 }\!\!\times\!\!\text{ 10}\]

Ans: Calculating the value,

$168.07\times 10=1680.7$

(v) \[\text{31}\text{.1 }\!\!\times\!\!\text{ 100}\] 

Ans: Calculating the value,

$31.1\times 100=3110.0$

(vi) \[\text{156}\text{.1 }\!\!\times\!\!\text{ 100}\] 

Ans: Calculating the value,

$156.1\times 100=15610.0$

(vii) \[\text{3}\text{.62 }\!\!\times\!\!\text{ 100}\] 

Ans: Calculating the value,

$3.62\times 100=362.0$

(viii) \[\text{43}\text{.07 }\!\!\times\!\!\text{ 100}\] 

Ans: Calculating the value,

$43.07\times 100=4307.0$

(ix) \[\text{0}\text{.5 }\!\!\times\!\!\text{ 10}\] 

Ans: Calculating the value,

$0.5\times 10=5.0$ 

(x) \[\text{0}\text{.08 }\!\!\times\!\!\text{ 10}\] 

Ans: Calculating the value,

$0.08\times 10=0.80$ 

(xi) \[\text{0}\text{.9 }\!\!\times\!\!\text{ 100}\]

Ans: Calculating the value,

$0.9\times 100=90.0$

(xii) \[\text{0}\text{.03 }\!\!\times\!\!\text{ 1000}\] 

Ans: Calculating the value,

$0.03\times 1000=30.0$ 

4. A two-wheeler covers a distance of\[\text{ }\!\!~\!\!\text{ 55}\text{.3 

km}\] 

in one litre of petrol. How much distance will it cover in \[\text{10 litres}\] of 

petrol?

Ans: Given: In one litre a two-wheeler covers a distance\[\text{ = 55}\text{.3 

km}\]

Since distance covered in one litre by a two-wheeler\[\text{ = 55}\text{.3 km}\]

\[\therefore \,\,\text{In 10 litrs, a two- wheeler covers a distance = 55}\text{.3 x 10 = 553}\text{.0 km}\] 

Hence, $553$ km distance will be covered by two-wheeler in $10$ litres of petrol.

5.  Find:

(i) $\text{2}\text{.5 }\!\!\times\!\!\text{ 0}\text{.3}$

Ans:  Calculating the value,

\[\text{2}\text{.5 x 0}\text{.3 = 0}\text{.75}\] 

(ii) $\text{0}\text{.1 }\!\!\times\!\!\text{ 51}\text{.7}$ 

Ans:  Calculating the value,

\[\text{0}\text{.1 x 51}\text{.7 = 5}\text{.17}\]

(iii) $\text{0}\text{.2 }\!\!\times\!\!\text{ 316}\text{.8}$ 

Ans: Calculating the value,

\[\text{0}\text{.2 x 316}\text{.8 = 63}\text{.36}\]

(iv) $\text{1}\text{.3 }\!\!\times\!\!\text{ 1}\text{.3}$ 

Ans: Calculating the value,

\[\text{1}\text{.3 x 3}\text{.1 = 4}\text{.03}\]

(v) $\text{0}\text{.5 }\!\!\times\!\!\text{ 0}\text{.05}$ 

Ans: Calculating the value,

\[\text{0}\text{.5 x 0}\text{.05 = 0}\text{.025}\]

(vi) $\text{11}\text{.2 }\!\!\times\!\!\text{ 0}\text{.15}$ 

Ans: Calculating the value,

\[\text{11}\text{.2 x 0}\text{.15 = 1}\text{.680 }\]

(vii) $\text{1}\text{.07 }\!\!\times\!\!\text{ 0}\text{.02}$ 

Ans: Calculating the value,

\[\text{1}\text{.07 x 0}\text{.02 = 0}\text{.0214}\]

(viii) $\text{10}\text{.05 }\!\!\times\!\!\text{ 1}\text{.05}$

Ans: Calculating the value,

\[\text{10}\text{.05 x 1}\text{.05 = 10}\text{.5525}\]

(ix) $\text{101}\text{.01 }\!\!\times\!\!\text{ 0}\text{.01}$ 

Ans: Calculating the value,

\[\text{101}\text{.01 x 0}\text{.01 = 1}\text{.0101}\]

(x) $\text{100}\text{.01 }\!\!\times\!\!\text{ 1}\text{.1}$

Ans: Calculating the value,

\[\text{100}\text{.01 x 1}\text{.1 = 110}\text{.11 }\]

Exercise 2.5

1. Find:

(i) \[\text{0}\text{.4  }\!\!\div\!\!\text{  2}\] 

Ans: Calculating the value,

\[0.4\div 2=\frac{4}{10}\times \frac{1}{2}=\frac{2}{10}=0.2\]

(ii) \[\text{0}\text{.35  }\!\!\div\!\!\text{  5}\] 

Ans: Calculating the value,

\[0.35\div 5=\frac{35}{100}\times \frac{1}{5}=\frac{7}{100}=0.07\]

(iii) \[\text{2}\text{.48  }\!\!\div\!\!\text{  4}\] 

Ans: Calculating the value,

\[2.48\div 4=\frac{248}{100}\times \frac{1}{4}=\frac{62}{100}=0.62\]

(iv) \[\text{65}\text{.4  }\!\!\div\!\!\text{  6}\] 

Ans: Calculating the value,

\[65.4\div 6=\frac{654}{10}\times \frac{1}{6}=\frac{109}{10}=10.9\]

(v) \[\text{651}\text{.2  }\!\!\div\!\!\text{  4}\] 

Ans: Calculating the value,

\[651.2\div 4=\frac{6512}{10}\times \frac{1}{4}=\frac{1628}{10}=162.8\]

(vi) \[\text{14}\text{.49  }\!\!\div\!\!\text{  7 }\] 

Ans: Calculating the value,

\[14.49\div 7=\frac{1449}{100}\times \frac{1}{7}=\frac{207}{100}=2.07\]

(vii) \[\text{3}\text{.96  }\!\!\div\!\!\text{  4}\]

Ans: Calculating the value,

\[3.96\div 4=\frac{396}{100}\times \frac{1}{4}=\frac{99}{100}=0.99\]

(viii) \[\text{0}\text{.80  }\!\!\div\!\!\text{  5}\] 

Ans: Calculating the value,

\[0.80\div 5=\frac{80}{100}\times \frac{1}{5}=\frac{16}{100}=0.16\]

2. Find:

(i) \[\text{4}\text{.8  }\!\!\div\!\!\text{  10}\] 

Ans: Performing the given calculation,

$4.8\div 10=\frac{4.8}{10}=0.48$

(ii) \[\text{52}\text{.5  }\!\!\div\!\!\text{  10}\] 

Ans: Performing the given calculation,

$52.5\div 10=\frac{52.5}{10}=5.25$

(iii) \[\text{0}\text{.7  }\!\!\div\!\!\text{  10}\] 

Ans: Performing the given calculation,

$0.7\div 10=\frac{0.7}{10}=0.07$

(iv) \[\text{33}\text{.1  }\!\!\div\!\!\text{  10}\]

Ans: Performing the given calculation,

$33.1\div 10=\frac{33.1}{10}=3.31$

(v) \[\text{272}\text{.23  }\!\!\div\!\!\text{  10}\] 

Ans: Performing the given calculation,

$272.23\div 10=\frac{272.23}{10}=27.223$

(vi) \[\text{0}\text{.56  }\!\!\div\!\!\text{  10 }\] 

Ans: Performing the given calculation,

$0.56\div 10=\frac{0.56}{10}=0.056$

(vii) \[\text{3}\text{.97  }\!\!\div\!\!\text{  10}\] 

Ans: Performing the given calculation,

$3.97\div 10=\frac{3.97}{10}=0.397$

3. Find:

(i) \[\text{2}\text{.7  }\!\!\div\!\!\text{  100}\] 

Ans: Converting the terms in fraction form and calculating the value,

$2.7\div 100=\frac{27}{10}\times \frac{1}{100}=\frac{27}{1000}=0.027$ 

(ii) \[\text{0}\text{.3  }\!\!\div\!\!\text{  100 }\]

Ans: Converting the terms in fraction form and calculating the value,

$0.3\div 100=\frac{3}{10}\times \frac{1}{100}=\frac{3}{1000}=0.003$

(iii) \[\text{0}\text{.78  }\!\!\div\!\!\text{  100}\] 

Ans: Converting the terms in fraction form and calculating the value,

$0.78\div 100=\frac{78}{10}\times \frac{1}{100}=\frac{78}{1000}=0.0078$

(iv) \[\text{432}\text{.6  }\!\!\div\!\!\text{  100}\] 

Ans: Converting the terms in fraction form and calculating the value,

$432.6\div 100=\frac{4326}{10}\times \frac{1}{100}=\frac{4326}{1000}=4.326$

(v) \[\text{23}\text{.6  }\!\!\div\!\!\text{  100}\] 

Ans: Converting the terms in fraction form and calculating the value,$23.6\div 100=\frac{236}{10}\times \frac{1}{100}=\frac{236}{1000}=0.236$

(vi) \[\text{98}\text{.53  }\!\!\div\!\!\text{  100}\] 

Ans: Converting the terms in fraction form and calculating the value,

$98.53\div 100=\frac{9853}{10}\times \frac{1}{100}=\frac{9853}{1000}=0.9853$

4. Find:

(i) \[\text{7}\text{.9  }\!\!\div\!\!\text{  1000}\] 

Ans: Converting the terms in fraction form and calculating the value,

$7.9\div 1000=\frac{79}{10}\times \frac{1}{1000}=\frac{79}{10000}=0.0079$ 

(ii) \[\text{26}\text{.3  }\!\!\div\!\!\text{  1000}\]

Ans: Converting the terms in fraction form and calculating the value,

$26.3\div 1000=\frac{263}{10}\times \frac{1}{1000}=\frac{263}{10000}=0.0263$

(iii) \[\text{38}\text{.53  }\!\!\div\!\!\text{  1000}\] 

Ans: Converting the terms in fraction form and calculating the value,

$38.53\div 1000=\frac{3853}{10}\times \frac{1}{1000}=\frac{3853}{10000}=0.03853$

(iv) \[\text{128}\text{.9  }\!\!\div\!\!\text{  1000}\] 

Ans: Converting the terms in fraction form and calculating the value,

$128.9\div 1000=\frac{1289}{10}\times \frac{1}{1000}=\frac{1289}{10000}=0.1289$

(v) \[\text{0}\text{.5  }\!\!\div\!\!\text{  1000}\] 

Ans: Converting the terms in fraction form and calculating the value,

$0.5\div 1000=\frac{5}{10}\times \frac{1}{1000}=\frac{5}{10000}=0.0005$

5. Find:

(i) \[\text{7  }\!\!\div\!\!\text{  3}\text{.5}\] 

Ans: Converting the terms in fraction form and calculating the value,

$7\div 3.5=7\div \frac{35}{10}=7\times \frac{10}{35}=\frac{10}{5}=2$

(ii) \[\text{36  }\!\!\div\!\!\text{  0}\text{.2 }\]

Ans: Converting the terms in fraction form and calculating the value,

$36\div 0.2=36\div \frac{2}{10}=36\times \frac{10}{2}=18\times 10=180$

(iii) \[\text{3}\text{.25  }\!\!\div\!\!\text{  0}\text{.5}\]  

Ans: Converting the terms in fraction form and calculating the value,$3.25\div 0.5=\frac{325}{100}\div \frac{5}{10}=\frac{325}{100}\times \frac{10}{5}=\frac{65}{10}=6.5$

(iv) \[\text{30}\text{.94  }\!\!\div\!\!\text{  0}\text{.7}\]

Ans: Converting the terms in fraction form and calculating the value,

$30.94\div 0.7=\frac{3094}{100}\div \frac{7}{10}=\frac{3094}{100}\times \frac{10}{7}=\frac{442}{10}=44.2$

(v) \[\text{0}\text{.5  }\!\!\div\!\!\text{  0}\text{.25 }\] 

Ans: Converting the terms in fraction form and calculating the value,$0.5\div 0.25=\frac{5}{10}\div \frac{25}{100}=\frac{5}{10}\times \frac{100}{25}=\frac{10}{5}=2$

(vi) \[\text{7}\text{.75  }\!\!\div\!\!\text{  0}\text{.25}\] 

Ans: Converting the terms in fraction form and calculating the value,

$7.75\div 0.25=\frac{775}{100}\div \frac{25}{100}=\frac{775}{100}\times \frac{100}{25}=31$

(vii) \[\text{76}\text{.5  }\!\!\div\!\!\text{  0}\text{.15}\] 

Ans: Converting the terms in fraction form and calculating the value,

$76.5\div 0.15=\frac{765}{100}\div \frac{15}{100}=\frac{765}{10}\times \frac{100}{15}=51\times 10=510$

(viii) \[\text{37}\text{.8  }\!\!\div\!\!\text{  1}\text{.4}\]

Ans: Converting the terms in fraction form and calculating the value,

$37.8\div 1.4=\frac{378}{10}\div \frac{14}{10}=\frac{378}{10}\times \frac{10}{14}=27$

(ix) \[\text{2}\text{.73  }\!\!\div\!\!\text{  1}\text{.3 }\] 

Ans: Converting the terms in fraction form and calculating the value,

$2.73\div 1.3=\frac{273}{100}\div \frac{13}{10}=\frac{273}{100}\times \frac{10}{13}=\frac{21}{10}=2.1$

6. A vehicle covers a distance of \[\text{43}\text{.2 km}\] in

\[\text{2}\text{.4}\]litres of petrol. How much distance will it cover in one 

litre 

petrol?

Ans: Given:\[\,\,\,\text{In 2}\text{.4 litres of petrol, distance covered by the vehicle = 43}\text{.2 km}\]

Since,\[\,\,\,\text{In 2}\text{.4 litres of petrol, distance covered by the vehicle = 43}\text{.2 km}\]

\[\therefore \,\,\text{In 1 litre of petrol, distance covered by the vehicle = 43}\text{.2  }\!\!\div\!\!\text{  2}\text{.4}\] 

Performing the required calculations,

$=\frac{432}{10}\div \frac{24}{10}=\frac{432}{10}\times \frac{24}{10}$ 

$\text{=18}\,\text{km}$ 

Hence, the vehicle can cover \[\text{18 km}\] distance in one litre of petrol.

NCERT Solutions for Class 7 Chapter 2 Maths PDF Download

2.1 Introduction

In NCERT Solutions Class 7 Chapter 2 Maths, students will learn about fractions and decimals. In junior classes, students have learned about what is a fraction and its types: proper, improper, mixed fractions, etc. Now, in class 7, we are going to learn about multiplication and division of fractions. The concept of fractions mainly focuses on the ratios and proportions, how to distribute etc. At the same time, decimals are the accurate values obtained after the division.

2.2 Recollect

In NCERT Solutions Class 7 Maths Chapter 2, students need to think again on the topics they have learned so far in the previous classes. These include representation of fractions on the number line, ordering of fractions, addition and subtraction of fractions, decimals and their additions, how to keep a point, etc. These are reminded in the first two exercises.

2.3 Multiplication of Fractions

In this section, students can understand how to multiply two fractions. If students have values like a and b, they can say ab is the product of a and b. If the values are like p/q, a/b then, how can we multiply? To multiply these fractions, it has two different methods. One is by using a  whole number and the other is by using a portion.

2.3.1 Multiplication of Fractions Using the Whole Number

Here, let us see what Fraction tells us? It explains that a down part is a whole number (except zero) and the upper part is the integer. In a fraction, the down part is known as the denominator whereas the upper part is the numerator. We use a whole number to multiply fractions if they are the same. For instance, let's say we have p/q. Then we can multiply with the whole number as 3*p/q. It is also applicable for improper or mixed fractions. But students need to make them into simpler forms before multiplying.

2.3.1 Multiplication of Fractions Using the Fraction

In this section, students can learn how to multiply two fractions when they are dissimilar. Students use a fraction to multiply them. The formula for multiplying two fractions is,(product of numerators)/(product of denominators).

The resultant product is less than the two fractions if we multiply two proper fractions. On the other hand, the result is greater than the two fractions if we multiply two improper fractions.

2.4 Division of Fractions

Let's discuss the division of fractions. Students can divide a fraction by a whole number and a whole number by a fraction. Here is a particular case to keep in mind. If two fractions for which numerator and denominator are in reverse order, then they are called reciprocals to each other.  Their product is always 1.

In the same way, while dividing mixed fractions with a whole number, students need to change the mixed fraction into improper fractions. Then it is easy to divide and solve. Next, we have to learn to divide a fraction with another fraction by changing one of the fractions into its reciprocal form.

The three concepts are explained differently in the NCERT Solutions for Class 7 Maths Chapter 2 PDF book available on Vedantu for students to go through if necessary.

2.5 Recalling Decimals

Decimals are the proper forms to represent the results obtained from multiplication and division. Placing the point in between numbers plays a vital role. One can express the heights, distances, weights,  measuring values, interest rates, shares, and fractions, also using decimals. To change the place value of the point, we can multiply by 10,100,...... Let's have a glance at the addition and subtraction of decimals.

Overview of Deleted Syllabus for CBSE Class 7 Maths Chapter 2 Fractions and Decimals

Class 7 Maths Chapter 2: Exercises Breakdown

Conclusion

NCERT Solutions for Chapter 2 fraction and decimals Class 7 offers practice problems and clear explanations to help master these concepts. Students should focus on fraction addition, subtraction, multiplication, and division for both like and unlike denominators. They should also be able to convert between fractions and decimals easily and understand relative fraction sizes. By carefully working through NCERT Class 7 Maths Chapter 2 Exercises, students can improve their knowledge and prepare for exams.

Other Study Material for CBSE Class 7 Maths Chapter 2

Chapter-Specific NCERT Solutions for Class 7 Maths

Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for NCERT Class 7 Maths

Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.