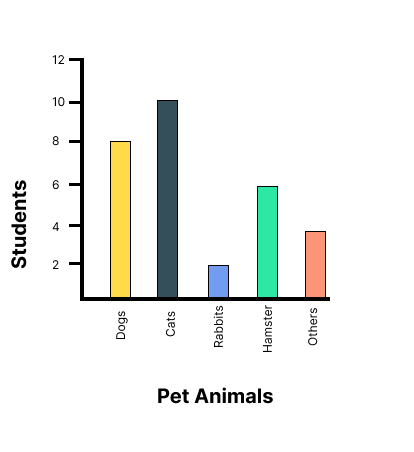
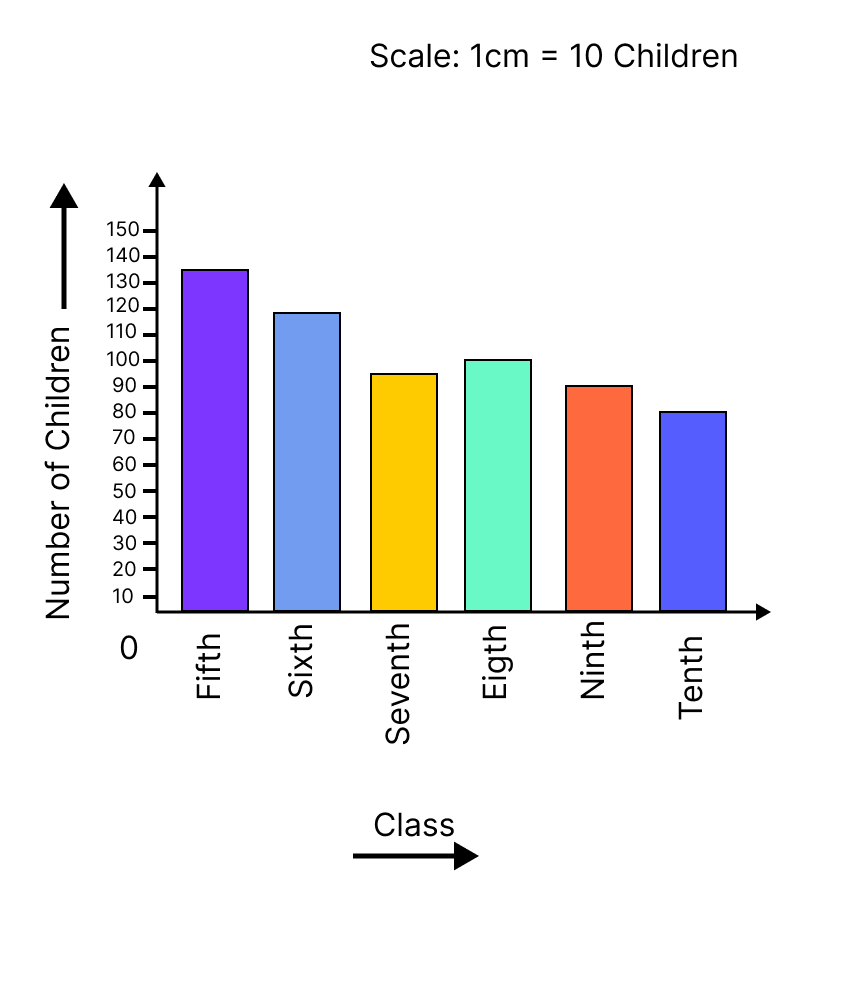
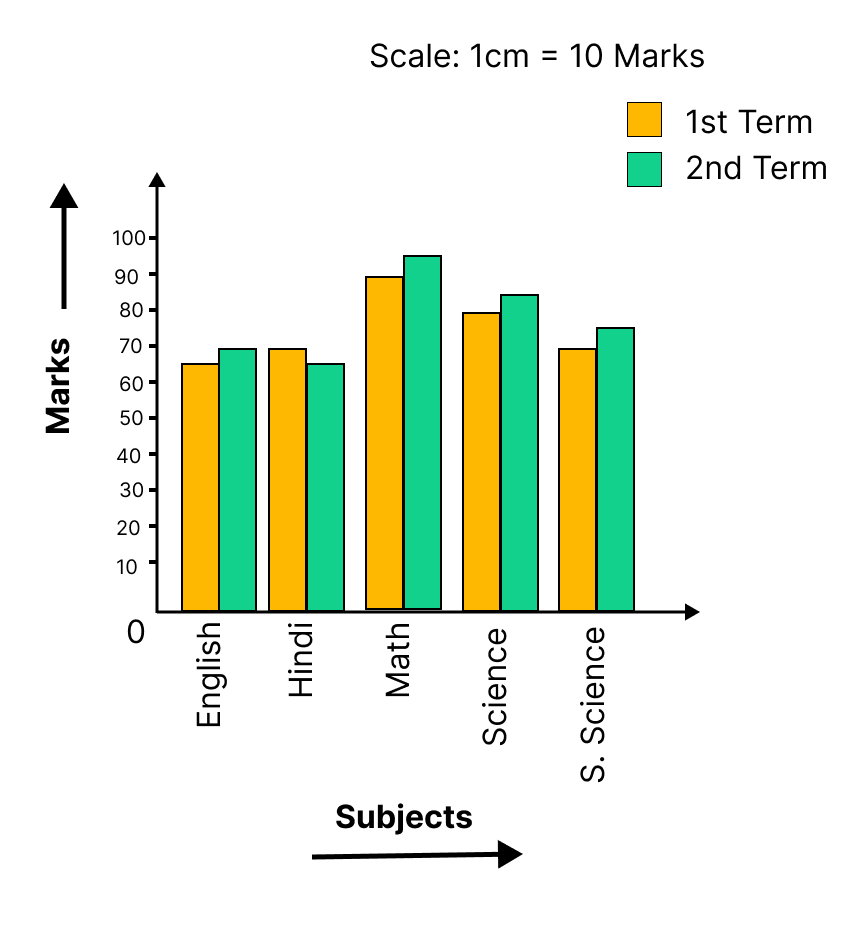
Data Handling - Exercise-wise Questions and Answers For Class 7 Maths - Free PDF Download
FAQs on NCERT Solutions For Class 7 Maths Chapter 3 Data Handling (2025-26)
1. Where can I find accurate and step-by-step NCERT Solutions for Class 7 Maths Chapter 3 for the 2025-26 session?
Vedantu offers comprehensive NCERT Solutions for Class 7 Maths Chapter 3, Data Handling, which are fully updated for the CBSE 2025-26 syllabus. These solutions are prepared by subject matter experts and provide a detailed, step-by-step methodology for solving every question in the NCERT textbook, ensuring students can learn the correct problem-solving approach.
2. How do the NCERT Solutions for Chapter 3 explain the correct method for calculating the mean?
The NCERT solutions clearly demonstrate the method for calculating the mean or average of a dataset. The process is broken down into simple steps:
- First, find the sum of all the given observations.
- Next, count the total number of observations.
- Finally, divide the sum of observations by the number of observations to find the arithmetic mean.
3. What is the correct procedure for finding the mode and median of a dataset as shown in the Chapter 3 solutions?
As per the NCERT solutions, the first and most critical step is to arrange the given data in ascending or descending order. After arranging the data:
- The mode is the observation that occurs most frequently.
- The median is the value of the middle-most observation. If there is an even number of observations, the median is the average of the two middle values.
4. How many exercises are there in Class 7 Maths Chapter 3, and do the provided solutions cover all questions?
The NCERT textbook for Class 7 Maths Chapter 3, Data Handling, contains four exercises: 3.1, 3.2, 3.3, and 3.4. Vedantu's NCERT Solutions provide complete, expert-verified answers for every single question across all four exercises, ensuring comprehensive coverage of the chapter.
5. How do the NCERT Solutions demonstrate the method for constructing a double bar graph?
The solutions provide a clear, step-by-step guide for creating a double bar graph, which is used to compare two sets of data. The method involves choosing an appropriate scale, drawing and labelling the X and Y axes, and then drawing pairs of bars for each category. Using different colours or patterns for the bars in each pair is essential to distinguish between the two data sets being compared.
6. Why is it important to follow the step-by-step methods shown in the NCERT solutions for Data Handling?
Following the step-by-step methods is crucial as it aligns with the CBSE evaluation pattern. Examiners look for a logical and structured approach, not just the final answer. Using the correct methodology for finding mean, median, mode, or drawing graphs ensures you demonstrate a clear understanding and can score full marks for the question.
7. How do the NCERT Solutions help students decide when to use mean, median, or mode?
By solving the diverse problems in the chapter using the solutions, students learn the appropriate contexts for each measure of central tendency. The mean is best for data sets without extreme values. The median is a better representative when there are outliers that might skew the result. The mode is most useful for identifying the most frequent or popular item in a set. The solutions help clarify these applications through practical examples.
8. What are the key topics for which the NCERT Solutions for Class 7 Maths Chapter 3 provide problem-solving methods?
The NCERT Solutions for this chapter provide detailed methods for solving problems related to key concepts such as:
- Organising raw data into frequency distribution tables.
- Calculating the range of a dataset.
- Finding the measures of central tendency: mean, median, and mode.
- Drawing and interpreting bar graphs and double bar graphs.
- Understanding and calculating basic chance and probability.
9. How do the solutions for Exercise 3.4 help in building a foundational understanding of probability?
The solutions for Exercise 3.4 methodically break down the concept of probability. They teach students how to first identify the total number of possible outcomes in a situation and then determine the number of outcomes that are favourable to a specific event. By showing how to calculate the ratio of (Favourable Outcomes) / (Total Outcomes), the solutions provide a clear and repeatable method for understanding the basics of probability.