Maths Class 8 Chapter 3 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2 (2025-26)
1. How do I find stepwise NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.1, 3.2, 3.3, and 3.4 as per the CBSE 2025–26 syllabus?
You can access stepwise NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.1, 3.2, 3.3, and 3.4 on trusted NCERT-aligned platforms like Vedantu and Tiwari Academy. These solutions are structured with detailed steps for each question, adhering to the latest CBSE 2025–26 format. Each answer follows the official NCERT answer method, ensuring clarity and accuracy for effective exam preparation.
2. Can I download the NCERT Solutions for Class 8 Maths Chapter 3 (Understanding Quadrilaterals) PDF for offline study?
Yes, you can easily download the NCERT Solutions for Class 8 Maths Chapter 3 PDF from Vedantu. The downloaded file contains complete, exercise-wise solutions prepared according to the official NCERT answer key, helping you practice offline and revise before exams.
3. Are the provided NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.3 and 3.4 in accordance with the CBSE and NCERT answer pattern?
Absolutely, all NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.3 and 3.4 are prepared strictly as per NCERT and CBSE-approved formats. The solutions clearly mention steps, diagrams (where needed), and reasoning, matching the latest CBSE guidelines for the 2025–26 session.
4. What is the method used to solve angle sum property questions in NCERT Class 8 Maths Chapter 3?
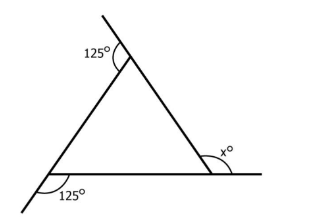
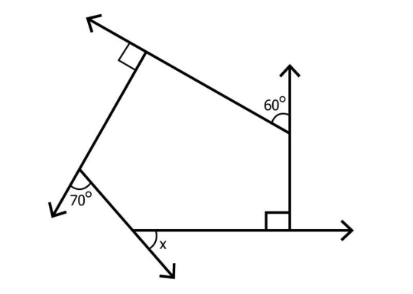
To solve angle sum property questions in NCERT Class 8 Maths Chapter 3, use the standard formula: Sum of the interior angles of a polygon = (number of sides – 2) × 180°. For quadrilaterals, this gives 360°, which must be used in each step as per the NCERT textbook solution format.
5. Are the NCERT Solutions for Understanding Quadrilaterals Chapter 3 available in Hindi medium as well?
Yes, NCERT Solutions for Class 8 Maths Chapter 3 are available in both English and Hindi medium. You can choose your preferred language to study the stepwise solutions, ensuring full understanding of all exercise and intext questions as per the official NCERT pattern.
6. How do I solve "Try These" in NCERT Class 8 Maths Chapter 3 following the textbook’s answer format?
To solve 'Try These' in NCERT Class 8 Maths Chapter 3, follow the NCERT textbook’s answer format: write the question number, solve each step methodically, and include diagrams or explanations as required by the exercise. Always check if the method matches the one shown in the official answer key.
7. Do these NCERT Solutions for Class 8 Maths Chapter 3 include extra questions and intext answers?
Yes, most NCERT Solutions for Class 8 Maths Chapter 3 cover all intext questions, exercise problems, and extra textbook questions that might be present, providing a comprehensive answer set aligned with the latest CBSE syllabus.
8. Where can I get official, CBSE-approved, chapter-wise solved answers for Class 8 Maths Chapter 3?
You can refer to Vedantu and similar reliable educational websites for official, CBSE-approved, chapter-wise NCERT Solutions for Class 8 Maths Chapter 3 (Understanding Quadrilaterals). The answers are curated by subject experts and strictly follow the NCERT stepwise explanation method.
9. Are diagrams required while answering questions on types of quadrilaterals in NCERT solutions?
Yes, for questions involving identification or properties of quadrilaterals, diagrams must be included as per NCERT answer pattern. Always draw neat labeled diagrams to secure full marks, since CBSE marking schemes allocate marks for this step.
10. How can these NCERT Solutions help me get full marks in Class 8 Maths exams?
By using these NCERT Solutions for Class 8 Maths Chapter 3, you learn the stepwise, CBSE-approved method to solve each problem, avoid common mistakes, and write answers in the exact format expected in exams, thus increasing your chances of scoring full marks.
11. Why does Exercise 3.2 in NCERT Class 8 Maths Chapter 3 focus heavily on properties of polygons?
Exercise 3.2 emphasizes the properties of polygons, such as the number of sides, diagonals, and angles, to strengthen understanding of how quadrilaterals fit within the broader concept of polygons. This is in line with the NCERT curriculum, ensuring students can apply the angle sum property logically and accurately.
12. How are the answers for NCERT Class 8 Maths Chapter 3 cross-checked for accuracy?
All NCERT Solutions for Class 8 Maths Chapter 3 are prepared by experienced teachers and reviewed for correctness using the official NCERT answer key and CBSE marking scheme. This ensures you get 100% accurate and exam-ready answers for each exercise and intext question.