NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry in Hindi PDF Download
प्रश्नावली 4.1
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज ABCD जिसमें
AB = 4.5cm, BC = 5.5cm,CD = 4cm,AD = 6cm तथा AC = 7 cm
उत्तर :
दिया गया है AB = 4.5cm, BC = 5.5cm, CD = 4, AC = 7 cm
रचना-
(i) सर्वप्रथम AB = 4.5 cm की एक रेखा खीची।
(ii)इसके बाद B को केंद्र मानकर 5.5 cm त्रिज्या का एक चाप खीचा।
(iii)उसी प्रकार A को भी केंद्र मानकर 7 cm त्रिज्या का एक चाप खीचा जो पूर्ववर्ती चाप को बिंदु C पर काटता है।
(iv)इस प्रकार हमें बिंदु C मिला |तथा BC और AC को मिलाया।
(v) पुन: A को केंद्र मानकर 6cm त्रिज्या का एक चाप खीचा तथा C को केंद्र मानकर 4 cm त्रिज्या का एक अन्य चाप खीचा जो इस चाप को बिंदु D पर काटता है।
(vi) इसके बाद AD और CD को मिलाया।
इस प्रकार हमें ABCD अभीष्ट चतुर्भुज प्राप्त हुआ।
(ii) चतुर्भुज JUMP जिसमें
JU = 3.5cm, UM = 4cm, MP = 5cm, PJ = 4.5cm तथा PU= 6.5cm
उत्तर:
दिया है JU = 3.5 cm, UM 4cm, MP = 5cm, PJ= 4.5cm,PU= 6.5cm
रचना-
(i) सर्वप्रथम JU = 3.5 cm का एक रेखा खीची ।
(ii)इसके बाद J को केंद्र मानकर 4.5 cm त्रिज्या का एक चाप खीचा उसी प्रकार U को केंद्र मानकर 6.5 cm त्रिज्या का एक चाप खीचा जो पूर्ववर्ती चाप को को बिंदु P पर काटता है।
(iii) अब PJ और PU को मिलाया।
(iv)पुन: U को केंद्र मानकर 4 cm त्रिज्या का एक चाप खीचा तथा P को केंद्र मानकर 5cm त्रिज्या का एक चाप खीचा जो इस चाप को बिंदु M पर काटता है।
(v)इसके बाद MP और MU को मिलाया।
इस प्रकार JUMP अभीष्ट चतुर्भुज है।
(iii) समांतर चतुर्भुज MORE जिसमें
OR= 6cm, EO = 7.5cm, MO= 7.5cm
उत्तर:
दिया गया है OR= 6cm, EO = 7.5cm, MO= 7.5cm
रचना-
(i) सर्वप्रथम OR = 6 cm की एक रेखा खीची।
(ii)इसके बाद O को केंद्र मानकर 7.5 cm त्रिज्या का एक चाप खीचा।
(iii)उसी प्रकार R को भी केंद्र मानकर 4.5 cm त्रिज्या का एक चाप खीचा जो पूर्ववर्ती चाप को बिंदु E पर काटता है।
(iv)इस प्रकार हमें बिंदु E मिला |तथा OE और RE को मिलाया।
(v) पुन: O को केंद्र मानकर 4.5cm त्रिज्या का एक चाप खीचा तथा E को केंद्र मानकर 6 cm त्रिज्या का एक अन्य चाप खीचा जो इस चाप को बिंदु M पर काटता है।
(vi) इसके बाद OM और EM को मिलाया।
इस प्रकार हमें MORE अभीष्ट चतुर्भुज प्राप्त हुआ।
(iv) सम चतुर्भुज BEST जिसमें
BE= 4.5cm, ET=6cm
उत्तर:
दिया गया है BE= 4.5cm, ET=6cm
रचना-
(i) सर्वप्रथम TE=6 cm की एक रेखा खीची।
(ii) इसके बाद TE क लम्ब समद्विभाजित किया|
(iii) E को केंद्र मानकर 4.5 cm त्रिज्या का एक चाप तथा उसी प्रकार T को भी केंद्र मानकर 4.5 cm त्रिज्या का एक चाप खीचा जो पूर्ववर्ती चाप को बिंदु S पर काटता है।
(iv)इस प्रकार हमें बिंदु S मिला |तथा SE और ST को मिलाया।
(v) पुन: E को केंद्र मानकर 4.5cm त्रिज्या का एक चाप खीचा तथा T को केंद्र मानकर 4.5 cm त्रिज्या का एक अन्य चाप खीचा जो इस चाप को बिंदु B पर काटता है।
(vi) इसके बाद EB और TB को मिलाया।
इस प्रकार हमें BEST अभीष्ट चतुर्भुज प्राप्त हुआ।
प्रश्नावली 4.2
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज LIFT जिसमें,
LI = 4cm, IF= 3 cm, TL= 2.5cm ,IT = 4cm, LF= 4.5cm
उत्तर:
दिया गया है LI = 4cm, IF= 3 cm, TL= 2.5cm ,IT = 4cm, LF= 4.5cm
रचना-
(i) सर्वप्रथम LI=4 cm की एक रेखा खीची।
(ii) L को केंद्र मानकर 4.5 cm त्रिज्या का एक चाप खीचा तथा उसी प्रकार I को भी केंद्र मानकर 3 cm त्रिज्या का एक चाप खीचा जो पूर्ववर्ती चाप को बिंदु F पर काटता है।
(iii)इस प्रकार हमें बिंदु F मिला |तथा FI और FL को मिलाया।
(iv) पुन: L को केंद्र मानकर 2.5cm त्रिज्या का एक चाप खीचा तथा I को केंद्र मानकर 4 cm त्रिज्या का एक अन्य चाप खीचा जो इस चाप को बिंदु T पर काटता है।
(v) इसके बाद LT और LI को मिलाया।
इस प्रकार हमें LIFT अभीष्ट चतुर्भुज प्राप्त हुआ।
(ii) चतुर्भुज GOLD जिसमें,
OL = 7.5cm, GL= 6cm, GD = 6cm, LD = 5cm, OD = 10cm
उत्तर:
दिया गया है OL= 7.5 cm, GL= 6cm, GD= 6cm, OD = 10cm
रचना-
(i) सर्वप्रथम OL = 7.5 cm की एक रेखा खीची।
(ii) L को केंद्र मानकर 5 cm त्रिज्या का एक चाप खीचा तथा उसी प्रकार O को भी केंद्र मानकर 10 cm त्रिज्या का एक चाप खीचा जो पूर्ववर्ती चाप को बिंदु D पर काटता है।
(iii)इस प्रकार हमें बिंदु D मिला |तथा OD और LD को मिलाया।
(iv) पुन: L को केंद्र मानकर 6 cm त्रिज्या का एक चाप खीचा तथा D को केंद्र मानकर 6 cm त्रिज्या का एक अन्य चाप खीचा जो इस चाप को बिंदु G पर काटता है।
(v) इसके बाद GD और GO को मिलाया।
इस प्रकार हमें GOLD अभीष्ट चतुर्भुज प्राप्त हुआ।
(iii) समलम्ब BEND जिसमें,
BN= 5.6cm, DE= 6.5cm
उत्तर:
दिया गया है BN= 5.6cm, DE= 6.5cm
रचना-
(i) सर्वप्रथम DE=6 cm की एक रेखा खीची।
(ii) इसके बाद DE क लम्ब समद्विभाजित किया|
(iii) o को केंद्र मानकर 2.8cm त्रिज्या का चाप काटा जो क्रमशः B और N पर कटते है।
(vi) सभी बिन्दुओ अर्थात BE, BD, ND, NE को मिलाया।
इस प्रकार हमें BEND अभीष्ट समलम्ब चतुर्भुज प्राप्त हुआ।
प्रश्नावली 4.3
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज MORE जिसमें,
MO=4cm, OR= 3cm, ∠M = 60°, ∠O = 105°, ∠R = 105°
उत्तर:
दिया गया है MO=4cm, OR= 3cm, ∠M = 60°, ∠O = 105°, ∠R = 105°
रचना-
(i) सर्वप्रथम MO= 6cm की एक रेखा खीची।
(ii) O पर 105° का कोण बनाया और इसे केंद्र मानकर 4.5 cm त्रिज्या का एक चाप खीचा जो R पर काटता है।
(ii) इसी प्रकार R पर भी 105° का कोण बनाया और भुजा RE को आगे बढ़ाया।
(iv) M पर 60° का कोण बनाया और M को E से मिलाया|इससे ME रेखा मिली।
(v) रेखा RE और ME को बढाया जो एक दूसरे को E पर प्रतिच्छेद करती हैं।
इस प्रकार हमें MORE अभीष्ट चतुर्भुज प्राप्त हुआ।
(ii) चतुर्भुज PLAN जिसमें,
PL= 4cm ,∠P = 90° ,∠N = 85° , OK= 7 cm, LA= 6.5cm ,∠A = 110
उत्तर:
दिया गया है PL= 4cm ,∠P = 90° ,∠N = 85° , OK= 7 cm, LA= 6.5cm ,∠A = 110°
∠L= 75°
रचना -
(i) सर्वप्रथम PL = 4 cm की एक रेखा खीची।
(ii) P पर समकोण बनाया तथा P और N को मिलाया
(iii) L पर 75° का कोण बनाया और L को केंद्र मानकर त्रिज्या 6 cm का एक चाप खीचा जो A पर काटता है।
(iv) A पर 110° बनाया जो N तक बढ़ाते है और भुजा AN को बढ़ाया।
यह भुजा PN को प्रतिच्छेद करती हैं।
इस प्रकार हमें PLAN अभीष्ट चतुर्भुज प्राप्त हुआ।
(iii) समांतर चतुर्भुज HEAR जिसमें,
HE= 5 cm, EA = 6cm,∠R=85°
उत्तर:
दिया गया है HE= 5 cm, EA = 6cm,∠R=85°
∠H=180 - 85= 85° (समान्तर चतुर्भुज के आसन्न कोण समकोण होते है)
रचना-
(i) सर्वप्रथम HE= 5 cm की एक रेखा खीची।
(ii) H पर 95° का कोण बनाया और H को केंद्र मानकर 6 cm त्रिज्या का एक चाप खीचा जो R पर काटता है। RH को मिलाया।
(iii) R और E पर 85° का कोण बनाया और E को केंद्र मानकर 6 cm त्रिज्या का चाप काटा
जो RA को A पर मिलता है|
(iv) RA को मिलाया ।
इस प्रकार हमें HEAR अभीष्ट समांतर चतुर्भुज प्राप्त हुआ।
(iv) आयत OKAY जिसमें,
OK=7 cm ,KA = 5cm
उत्तर:
दिया गया है OK= 7 cm, KA=5cm
रचना-
(i) सर्वप्रथम OK = 7 cm की एक रेखा खीची।
(ii) O और K पर 90° का कोण बनाया।
(iii) पुन: O को केंद्र मानकर 5cm त्रिज्या का एक चाप खीचा जो Y पर मिलता है तथा K को केंद्र मानकर त्रिज्या 5 cm का एक चाप खीचा जो A पर मिलता है।
(iv) Y और A को मिलाया।
इस प्रकार हमें OKAY अभीष्ट आयत प्राप्त हुआ।
प्रश्नावली 4.4
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज DEAR जिसमें,
DE= 4 cm, EA = 5cm, AR = 4.5cm,∠E = 60° ,∠A = 90°
उत्तर:
दिया गया है DE= 4 cm, EA = 5cm, AR = 4.5cm,∠E = 60° ,∠A = 90°
रचना-
(i) सर्वप्रथम DE = 4 cm की एक रेखा खीची ।
(ii) E पर 60° का कोण बनाया और भुजा AE को आगे बढ़ाया।
(iii) पुन: E को केंद्र मानकर 5cm त्रिज्या का एक चाप खीचा जो A पर मिलता है।
(iv) अब A पर 90° का कोण बनाया और इसको केंद्र मानकर 4.5 cm त्रिज्या का एक चाप खीचा जो R पर मिलता है।
इस प्रकार हमें DEAR अभीष्ट चतुर्भुज प्राप्त हुआ।
(ii) चतुर्भुज TRUE जिसमें,
TR= 3.5 cm,RU=3cm,UE = 4cm,∠R=75°,∠U = 120°
उत्तर:
दिया गया है TR= 3.5 cm,RU=3cm,UE = 4cm,∠R=75°,∠U = 120°
रचना-
(i)सर्वप्रथम TR पर 3.5cm की एक रेखा खीची।
(ii) R पर 60° का कोण बनाया और इसे केंद्र मानकर 3 cm त्रिज्या का एक चाप खीचा जो U पर मिलता है।
(iii) U पर 120° का कोण बनाया और भुजा UE को आगे बढ़ाया।
(iv) U को केंद्र मानकर 4 cm त्रिज्या का एक चाप बनाया
(v) अब UE और TE को मिलाया
इस प्रकार TRUE अभीष्ट चतुर्भुज प्राप्त हुआ।
प्रश्नावली 4.5
निम्नलिखित की रचना कीजिए:
1. एक वर्ग READ जिसमें RE = 5.1 cm है।
उत्तर:
दिया गया है RE = 5.1 cm
रचना-
(i)सर्वप्रथम RE= 5.1 cm की एक रेखा खीची।
(ii)E पर 90° का कोण बनाया और इसे केंद्र मानकर 5.1 cm त्रिज्या का एक चाप खीचा जो A पर मिलता है।
(iii) अब A को केंद्र मानकर 5.1 cm त्रिज्या का एक चाप खीचा और R को केंद्र मानकर 5.1 cm त्रिज्या का एक और चाप खीचा जो एक दूसरे को D पर काटते हैं।
(iv) अंत में AD और RD को मिलाया।
इस प्रकार READ अभीष्ट वर्ग प्राप्त हुआ।
2. एक सम चतुर्भुज जिनके विकर्णों की लंबाई 5.2 cm और 6.4cm है।
उत्तर:
दिया गया है विकर्णों की लंबाई AC=5.2 cm औरBD= 6.4cm
माना चतुर्भुज ABCD है
रचना-
(i) सर्वप्रथम AC = 5.2 cm की एक रेखा खीची तत्पश्चात उसका लंब समद्विभाजन किया।
(ii) BD विकर्ण का आधा माप लेकर O से 3.2 cm का चाप उपर और नीचे काटा| (सम चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं)
(iii) यह चाप बिंदु B और D पर कटते हैं। इन्हें मिलाया|
(iv) अंत में सभी भुजाओ को मिलाया।
इस प्रकार ABCD अभीष्ट सम चतुर्भुज प्राप्त हुआ।
3. एक आयत जिसकी आसन्न भुजाओं की लंबाइयाँ 5 cm और 4 cm है।
उत्तर:
माना आयात MNOP है तथा आसन्न भुजाए MN और MP है|
दिया गया है MN=5cm , MP=4cm
रचना-
(i) सर्वप्रथम MN = 5 cm की एक रेखा खीची ।
(ii) बिंदु M और N पर 90 का कोण बनाया।
(iii) अब M को केंद्र मानकर 4 cm त्रिज्या का एक चाप खीचा जो P पर काटता है
इसी प्रकार N को केंद्र मानकर 4cm त्रिज्या का एक चाप बनाया जो O पर काटता है।
(iv) MP और PO को मिलाया।
इस प्रकार MNOP अभीष्ट आयत प्राप्त हुआ|
4. एक समांतर चतुर्भुज OKAY जहाँ OK= 5.5 cm और KA = 4.2 cm है।
उत्तर:
दिया गया है OK=5.5cm और KA= 4.2cm
रचना-
(i) सर्वप्रथम OK=5.5 cm की एक रेखा खीची|
(ii) K पर 90° का कोण बनाया और K को भी केंद्र मानकर 4.2cm त्रिज्या का एक चाप खीचा जो A पर मिलता है
(iii)इसी प्रकार A को केंद्र मानकर 5.5 cm त्रिज्या का एक चाप खीचा और O को केंद्र मानकर 4.2cm त्रिज्या का एक चाप खीचा जो एक दूसरे को Y पर मिलते हैं। इन्हें मिलाया|
इस प्रकार OKAY अभीष्ट समांतर चतुर्भुज प्राप्त हुआ।
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry in Hindi
Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 8 Maths Chapter 4 solution Hindi mediums are created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 8 Maths Chapter 4 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.
NCERT Solutions for Class 8 Maths Chapter 4 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 8 Maths Practical Geometry solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that.
NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 8 Maths Practical Geometry in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 8 can download these solutions at any time as per their convenience for self-study purpose.
These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/ solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 8 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.
FAQs on NCERT Solutions for Class 8 Maths In Hindi Chapter 4 Practical Geometry
1. How can I score good marks in the Maths Class 8 CBSE?
In order to score good grades in the Class 8 examinations, it is important to acquaint oneself with the basic concepts and ideas that each chapter has to offer. The next step would include practicing these concepts to strengthen and retain what has been taught. The NCERT solutions that are available on the website of Vedantu (vedantu.com) will help in the understanding of the student. The easy and compact language comes as a cherry on the cake, which makes the grasping process even more easy and smooth. Moreover, every exercise has detailed and explanatory answers, helping the student in every step of his progress.
2. Where can I get solutions for NCERT Class 8 Maths chapter-wise?
Vedantu is a free web portal for CBSE students that provides free PDFs for practice. Vedantu also has an app of its own that is available on Google Playstore to download. The PDFs are available for every chapter and have detailed answers within them. These answers make it easier for the students to understand the practice exercises without having any doubts. These are designed by subject matter experts to help the student in better understanding. It prepares them in retaining these concepts and thereby scoring well in their examinations.
3. How should one prepare for the NCERT solutions for Class 8 Maths Chapter 4?
The very first thing would be to learn what Practical Geometry is and understand the basic and rudimentary concepts that come along with it. This can be achieved with the help of Vedantu, which is an online website (vedantu.com) that provides solutions and explanations for every chapter in the form of PDFs for free. Once the student is done with the understanding of these basic concepts, they can move on to practice the various exercises that are available in these PDFs. These exercises have detailed explanations helping students understand and retain what they learn.
4. Is it enough to study NCERT Solutions for Class 8 Maths Chapter 4?
The NCERT solutions are designed in such a way as to fulfill the demands and needs of the students. It has exercises with step-by-step explanations, helping the student to understand the concepts and ideas clearly and without any doubts. It has all the important and relevant study materials that will help the student in securing good grades in the exam. These solutions are made keeping in mind the patterns of questions that may be asked in the exam, and therefore the practice of these will help in improving the knowledge and skills of the students. So, the practice of the NCERT Solutions for Class 8 Maths Chapter 4 is enough for a student to score good grades.
5. What are the main concepts to understand Practical Geometry?
Some of the main concepts include:
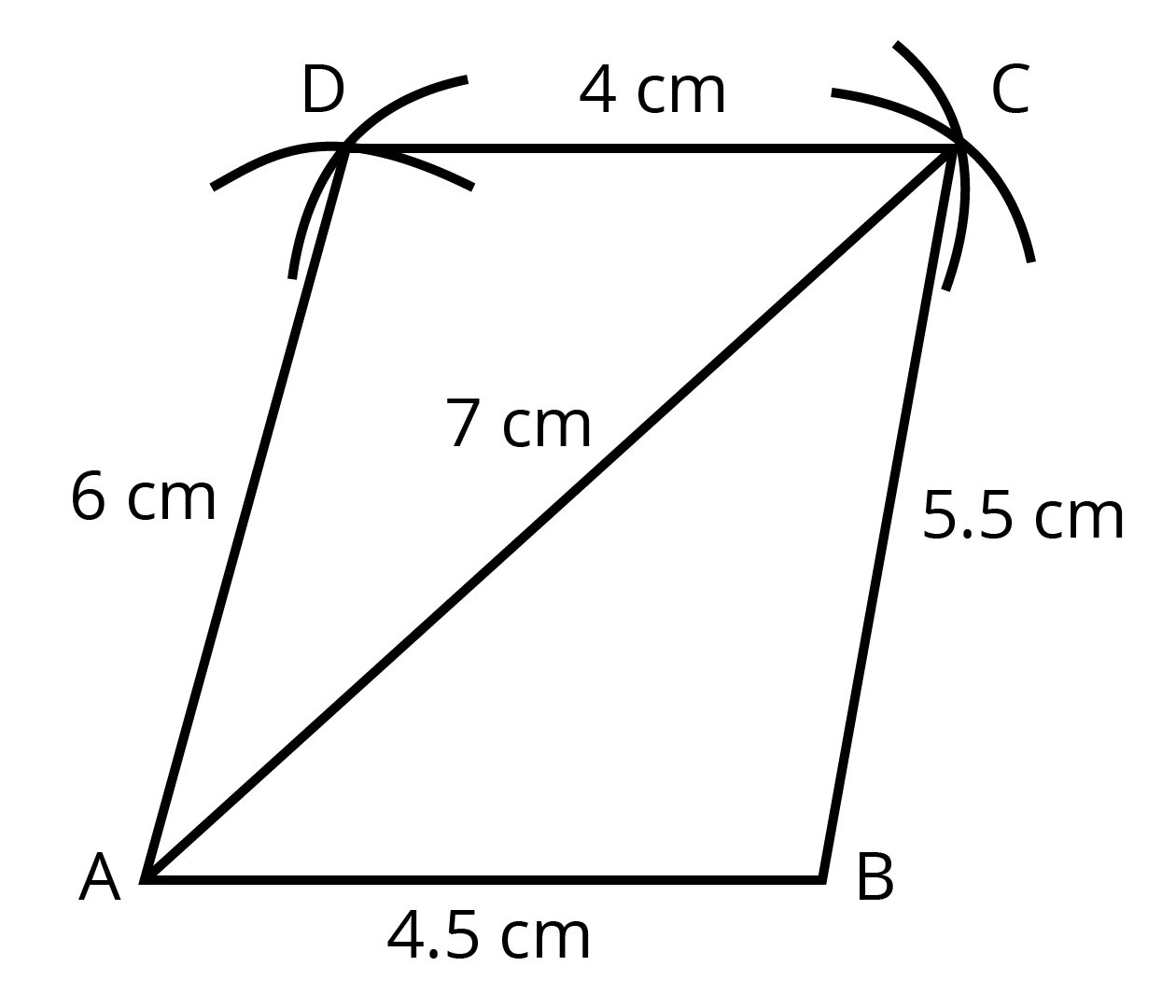
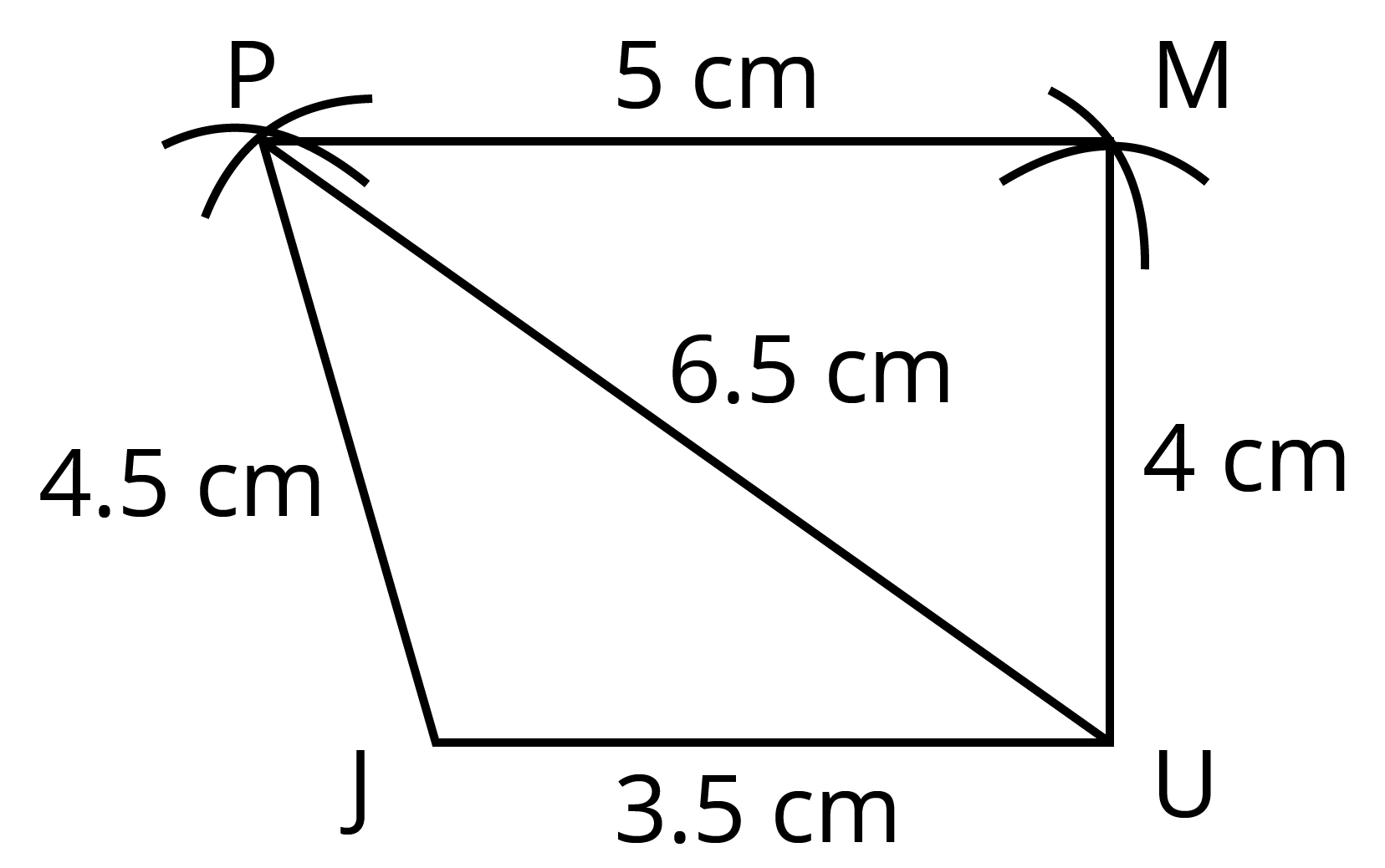
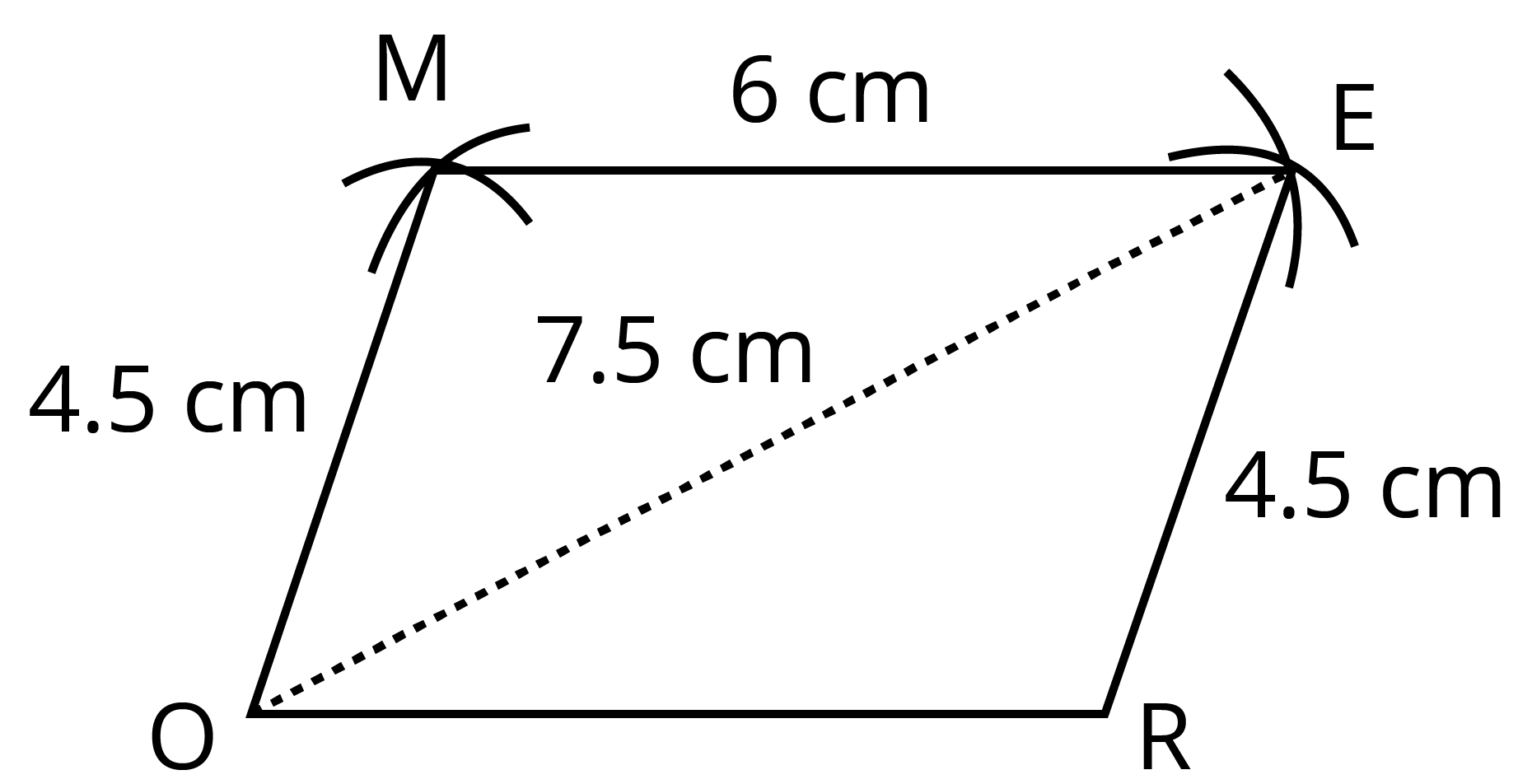
Five measurements define a quadrilateral uniquely.
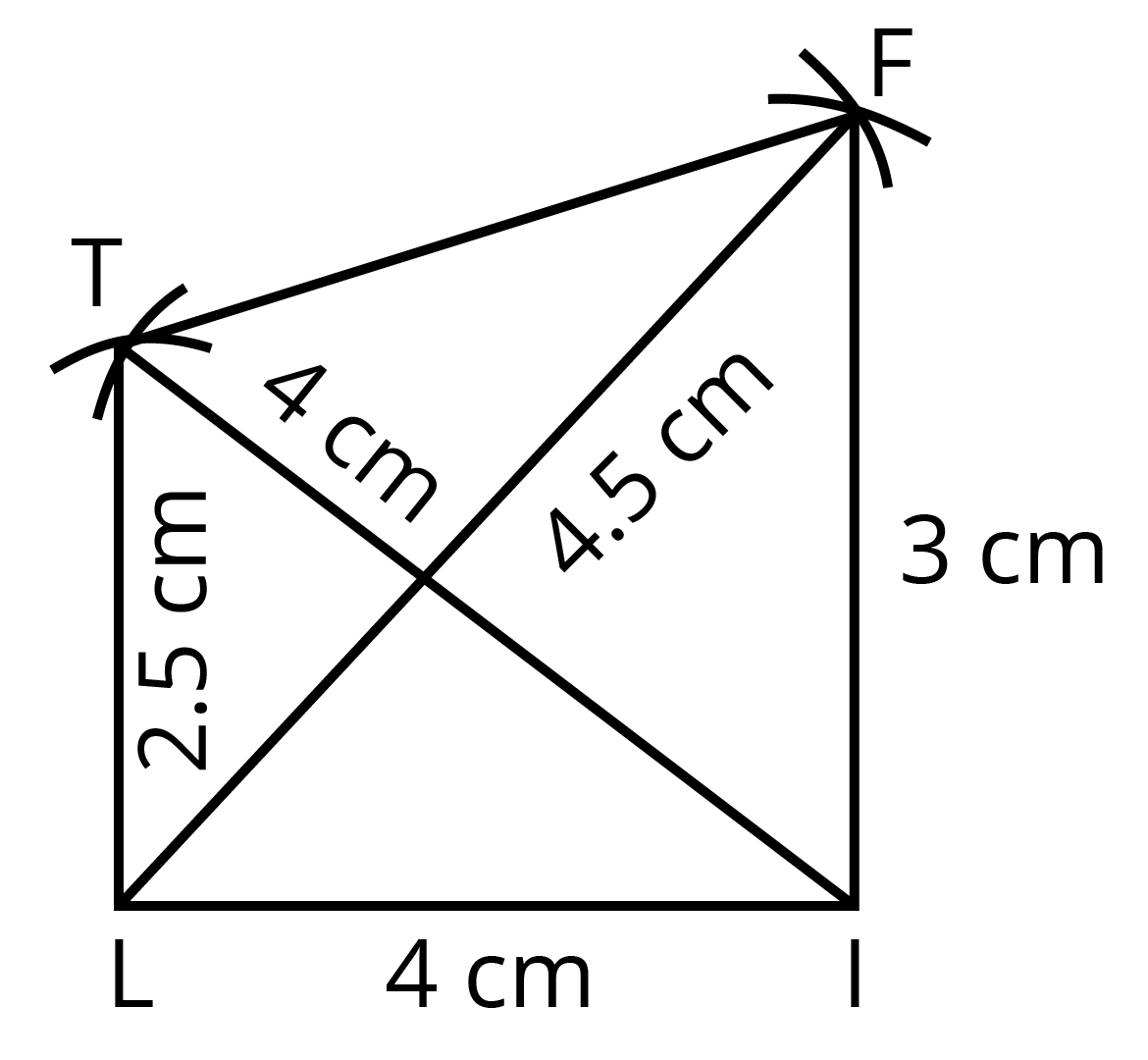
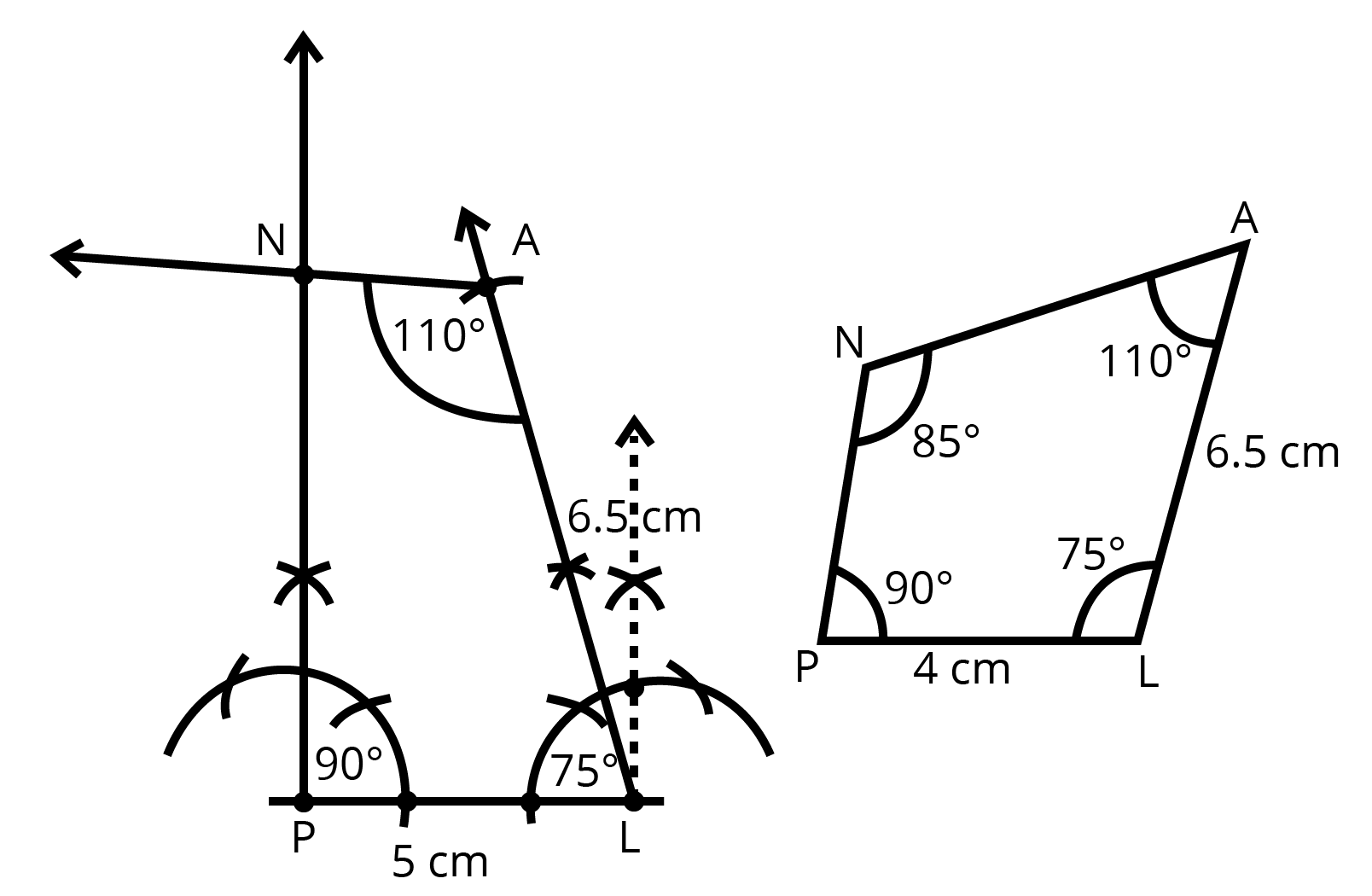
If the length of its four sides and diagonal is given, then a quadrilateral can be constructed uniquely
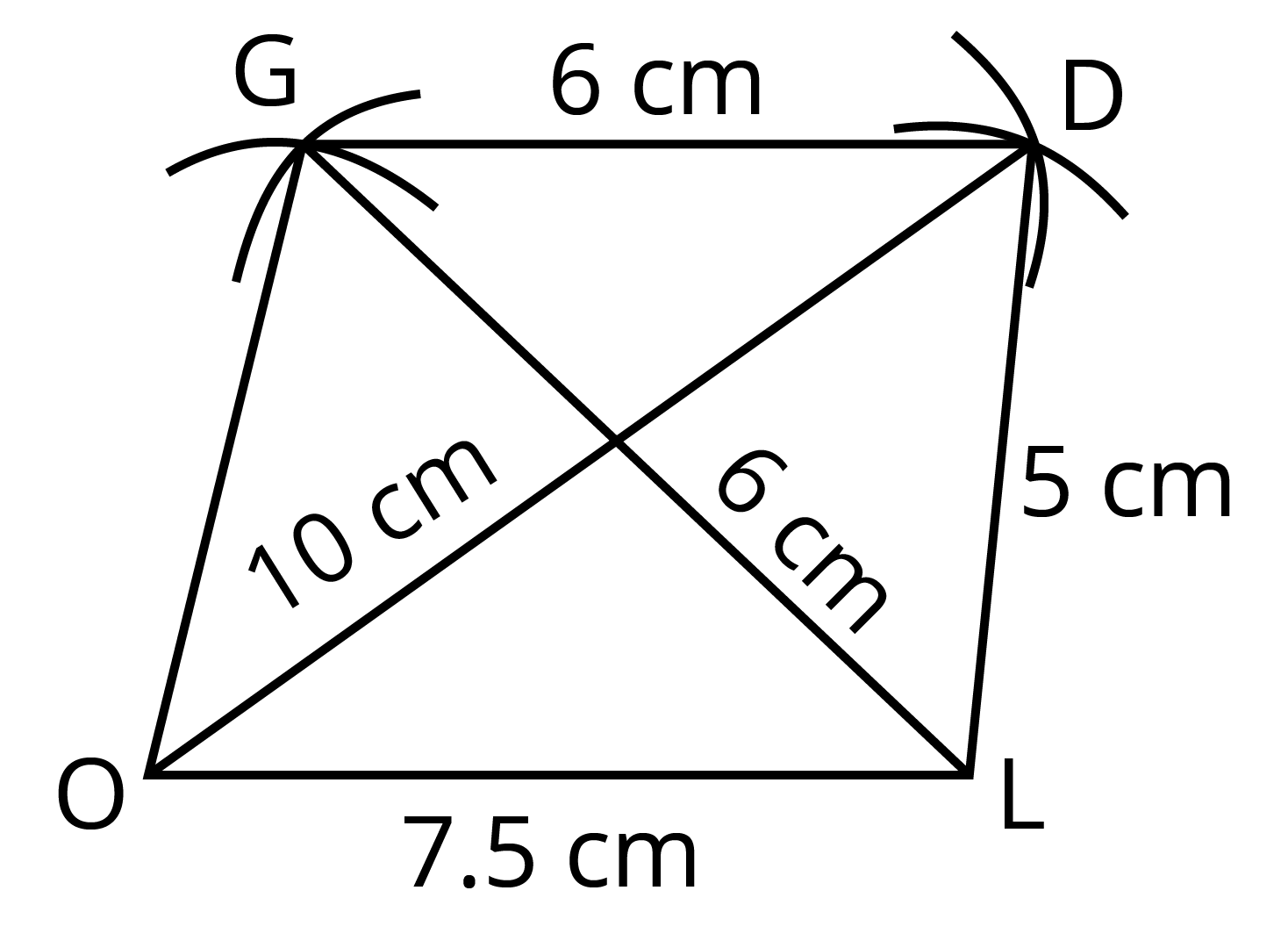
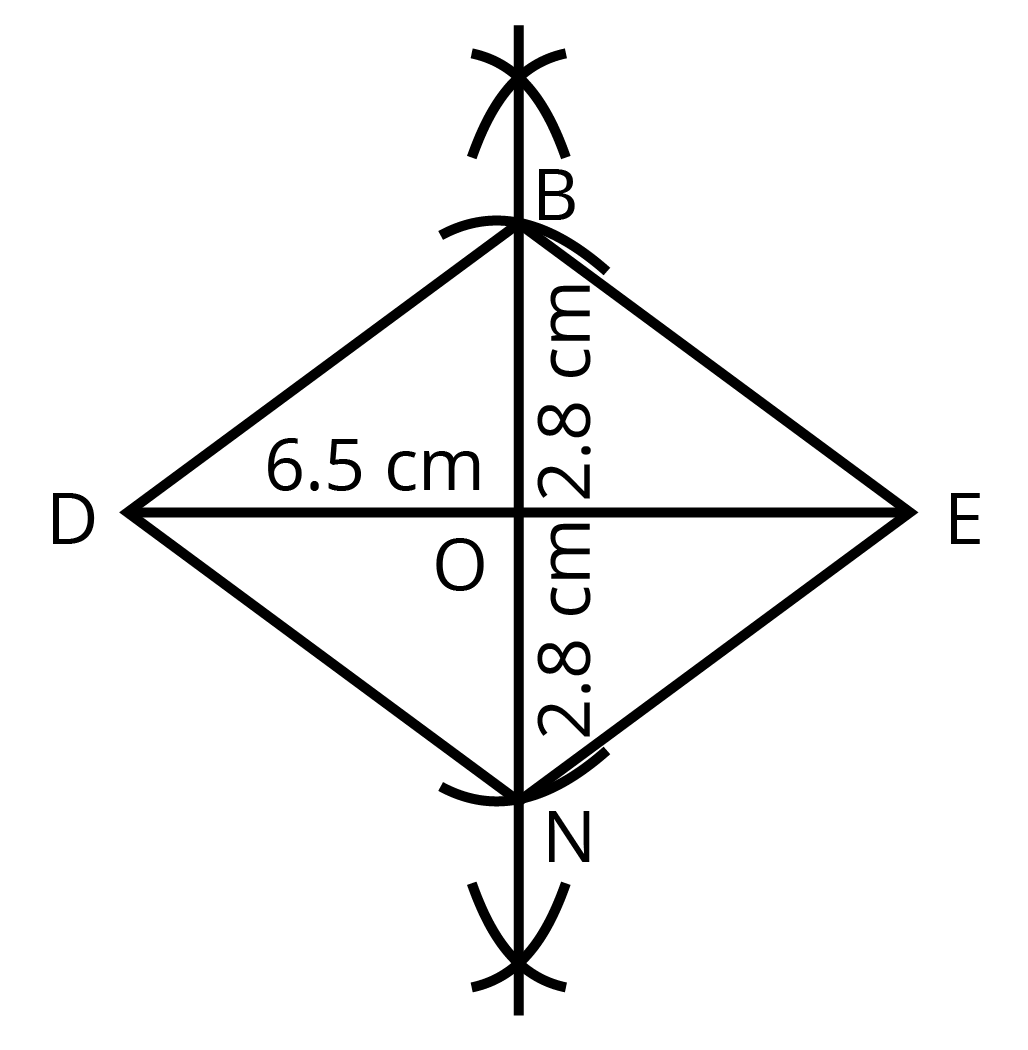
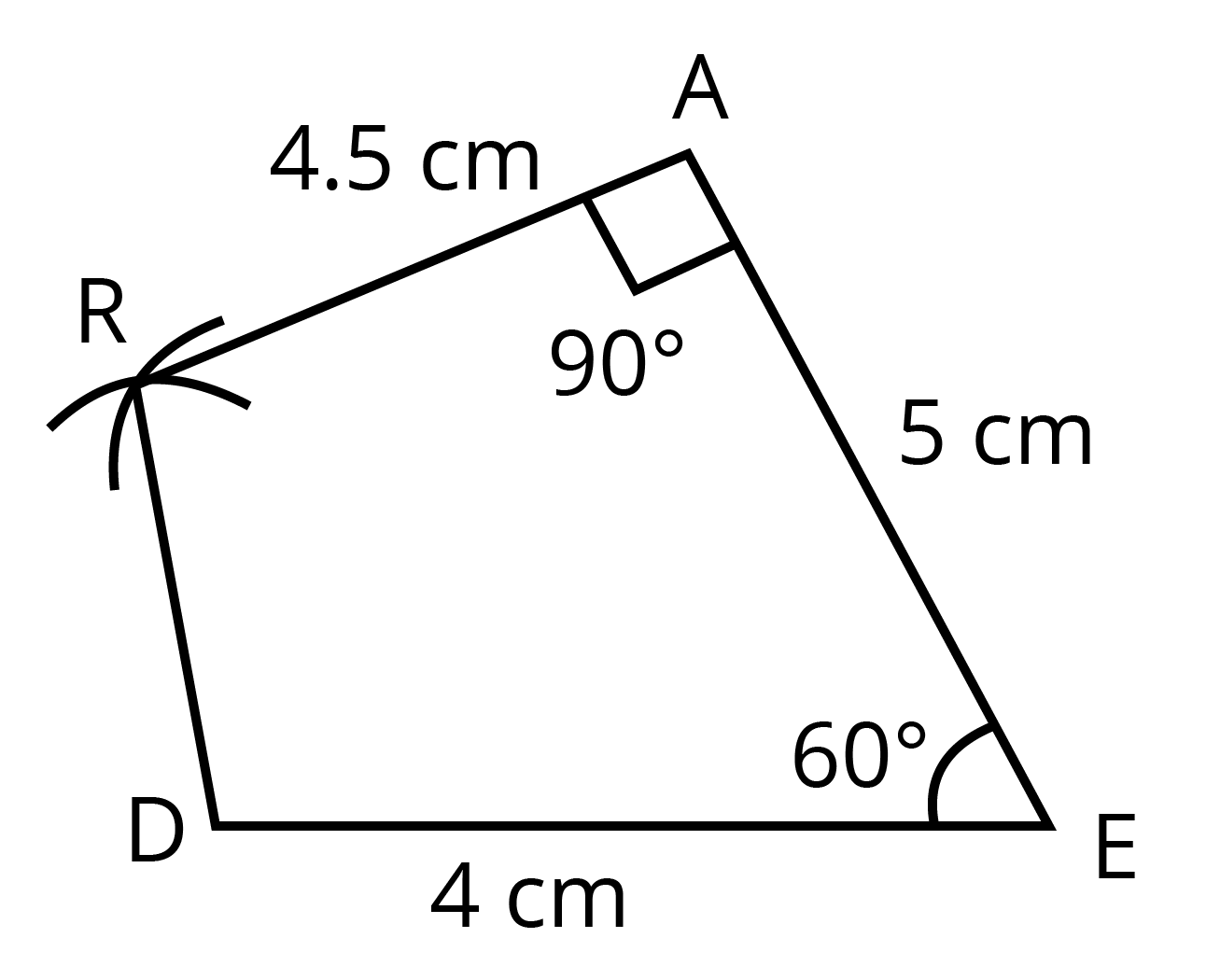
It can also be constructed uniquely if only three sides and two diagonals are known.
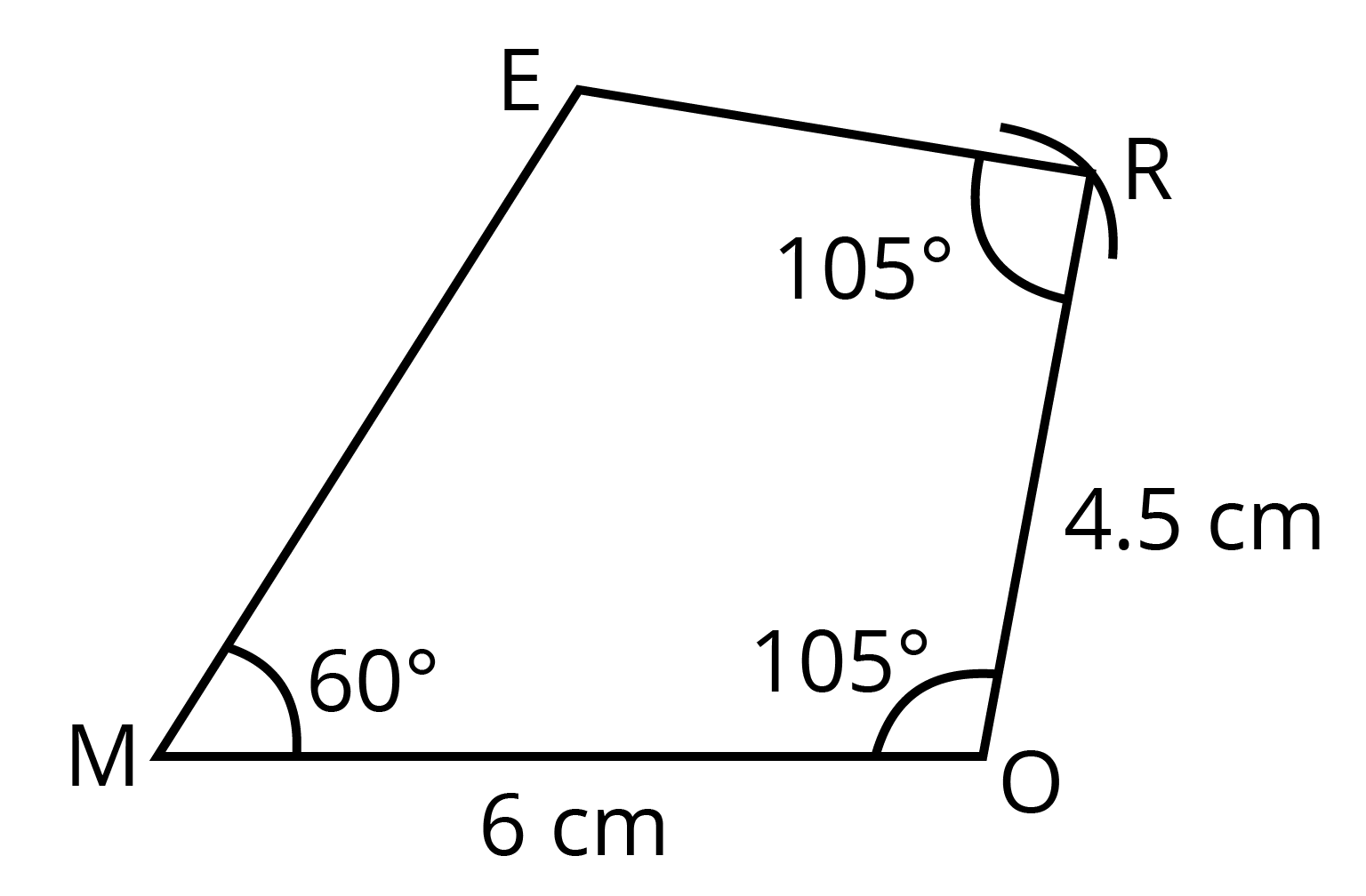
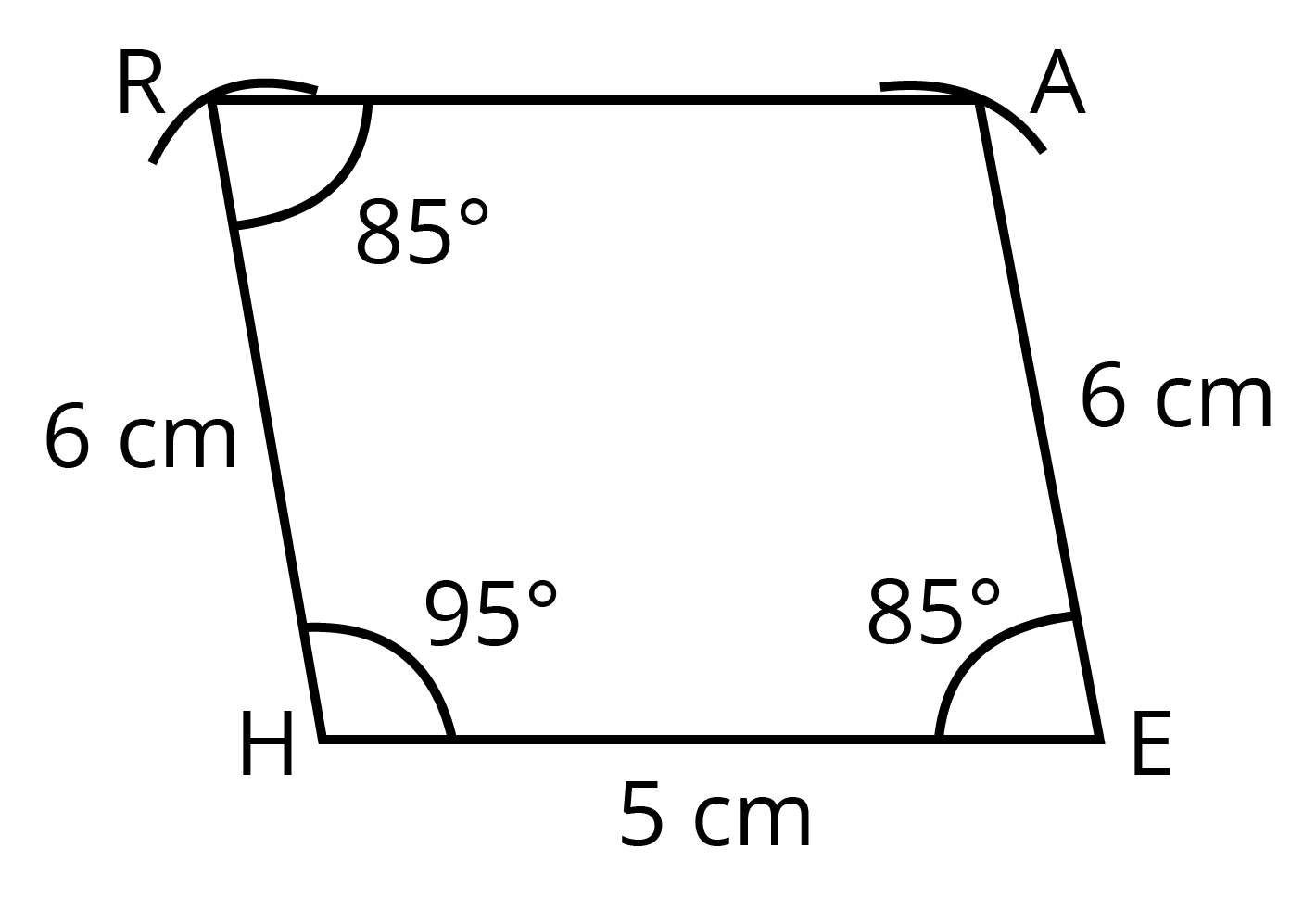
Also, if two adjacent sides and three angles are known, it can still be constructed uniquely.
Lastly, if three sides and two included angles are given, the quadrilateral can be constructed uniquely.
