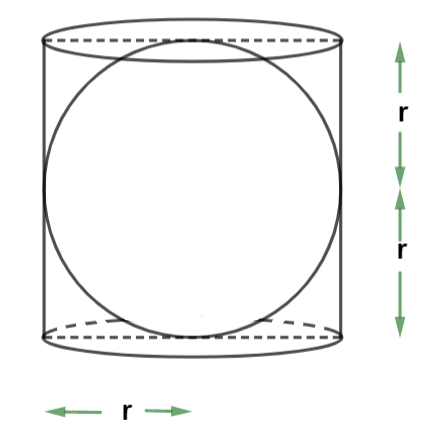
Class 9 Maths Exercise 11.2 – Surface Areas and Volumes Solutions
NCERT Solutions For Class 9 Maths Chapter 11 Surface Areas And Volumes Exercise 11.2 (2025-26)
FAQs on NCERT Solutions For Class 9 Maths Chapter 11 Surface Areas And Volumes Exercise 11.2 (2025-26)
1. What is covered in NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.2?
NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.2 cover all textbook questions from Surface Areas and Volumes, solved step by step as per the NCERT format.
2. Where can students find Class 9 Maths Exercise 11.2 solutions?
Students can find Class 9 Maths Exercise 11.2 solutions on Vedantu, where NCERT Solutions for Surface Areas and Volumes are presented in a clear, exam-oriented structure.
3. Are NCERT Solutions for Exercise 11.2 Class 9 Maths written as per CBSE standards?
Yes, NCERT Solutions for Exercise 11.2 Class 9 Maths are written according to CBSE answer-writing standards expected for Surface Areas and Volumes questions.
4. What type of questions are included in Class 9 Maths Chapter 11 Exercise 11.2?
Class 9 Maths Chapter 11 Exercise 11.2 includes only the questions prescribed by NCERT under the chapter Surface Areas and Volumes, all solved in the same order.
5. Who should use NCERT Solutions for Class 9 Maths Exercise 11.2?
NCERT Solutions for Class 9 Maths Exercise 11.2 are suitable for students who want accurate, NCERT-aligned answers for school work and exams in Surface Areas and Volumes.
6. How are answers presented in Class 9 Maths Exercise 11.2 solutions on Vedantu?
On Vedantu, Class 9 Maths Exercise 11.2 solutions are presented in a stepwise and neatly structured format, matching NCERT and CBSE expectations.
7. Do NCERT Solutions for Surface Areas and Volumes Exercise 11.2 follow the NCERT question sequence?
Yes, NCERT Solutions for Surface Areas and Volumes Exercise 11.2 strictly follow the same question numbering and sequence as the NCERT textbook.
8. Can Class 9 Maths Chapter 11 Exercise 11.2 solutions be used for school exams?
Yes, Class 9 Maths Chapter 11 Exercise 11.2 solutions can be confidently used for school exams as they are fully aligned with NCERT and CBSE guidelines.
9. How is Exercise 11.2 positioned within the chapter Surface Areas and Volumes?
Exercise 11.2 is a core part of Class 9 Maths Chapter 11 Surface Areas and Volumes, and its question formats are commonly assessed in schools.
10. Why do students prefer NCERT Solutions for Class 9 Maths Exercise 11.2 on Vedantu?
Students prefer NCERT Solutions for Class 9 Maths Exercise 11.2 on Vedantu because they offer accurate answers, clear step-by-step presentation, and strict alignment with the NCERT textbook.




















 Watch Video
Watch Video