Step-by-Step Solutions For Class 9 Maths Chapter 12 In Hindi - Free PDF Download
FAQs on NCERT Solutions For Class 9 Maths in Hindi Chapter 12 Heron's Formula (2025-26)
1. What is the main aim of NCERT Solutions for Class 9 Maths Chapter 12?
The main aim of NCERT Solutions for Class 9 Maths Chapter 12 is to make students capable of solving equations that have multiple functions along with its derivatives. A function’s derivative will help you in learning how to calculate the changing rate of any function. The answers have been put forward by experts who know how students can score high grades in the Class 9 exams. You can even get NCERT Solutions Class 9 Maths Chapter 12 in Hindi.
2. What are the key benefits of referring to NCERT Solutions for Class 9 Maths Chapter 12?
If you choose the NCERT Solutions for Class 9 Maths Chapter 12 on Vedantu, you unlock a number of advantages. The answers to each sum have been clarified in a lucid way so that it is easy for a student to get a hang of it. Experts at Vedantu have been tirelessly working towards creating answers that are more comprehensible for students. NCERT Solutions Class 9 Maths Chapter 12 in Hindi is also available for students.
3. Where to get the best NCERT Solutions for Chapter 12 of Class 9 Maths in Hindi?
The best place to get NCERT Solutions for Chapter 12 of Class 9 Maths in Hindi is Vedantu. You get full answers to the NCERT exercises from this chapter. Each and every topic is elaborately explained in Hindi and all the important examples have been touched upon so that you do not miss out on anything. Including the NCERT Solutions for Chapter 12 Maths in Hindi will upgrade your performance and increase your marks.
4. What are the important formulas in Class 9 Maths Chapter 12?
The important formulas that you need to study in Class 9 Maths Chapter 12 ‘Heron’s Formula’ are the area of a triangle (½ x base x height), Heron’s formula for calculating area of a triangle [√s(s - a)(s - b)(s - c)], and using the Heron’s formula to calculate the area of quadrilaterals. All the questions based on these formulas in the NCERT Maths Class 9 textbook have been methodically solved in Vedantu’s NCERT Solutions for Class 9 Maths Chapter 12.
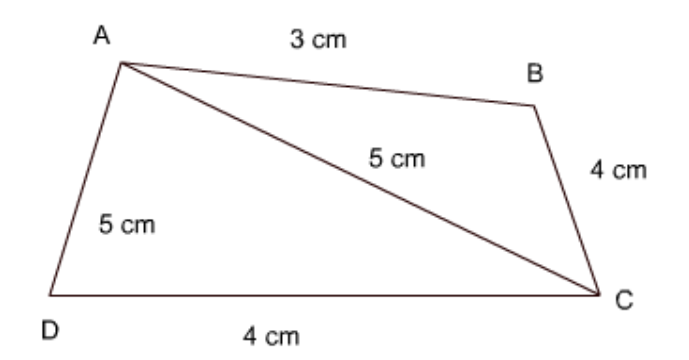
5. How can you calculate the area of a quadrilateral with Heron’s formula?
You can easily apply Heron’s formula (√s(s - a)(s - b)(s - c)) to the area of a quadrilateral with sides and one diagonal given. You have to divide the given quadrilateral into triangles and then apply Heron’s formula to calculate the area of these triangles. Once you have calculated the area of these triangles, you add all the areas to calculate the area of the quadrilateral. Refer to NCERT Solutions Class 9 Maths Chapter 12 for more such explanations.