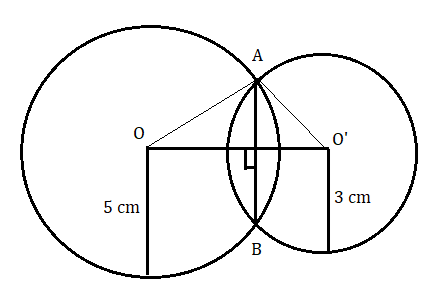
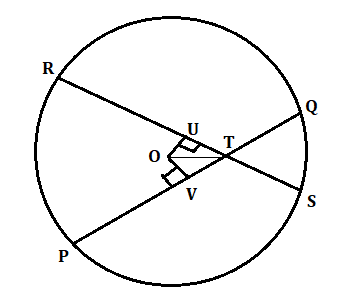
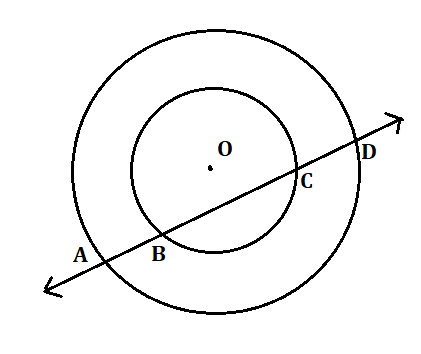
Class 9 Maths Exercise 9.2 – Circles Solutions
NCERT Solutions For Class 9 Maths Chapter 9 Circles Exercise 9.2 (2025-26)
FAQs on NCERT Solutions For Class 9 Maths Chapter 9 Circles Exercise 9.2 (2025-26)
1. What does Exercise 9.2 include in Class 9 Maths?
Exercise 9.2 is part of Class 9 Maths Chapter 9 – Circles and includes all NCERT textbook questions that are solved step by step in the official solutions.
2. Where can students find solutions for Class 9 Maths Exercise 9.2?
Students can find complete solutions for Class 9 Maths Exercise 9.2 on Vedantu, where answers are presented exactly as per the NCERT textbook structure.
3. Are the solutions for Class 9 Maths Exercise 9.2 aligned with CBSE standards?
Yes, the solutions for Class 9 Maths Chapter 9 Exercise 9.2 are written according to CBSE answer-writing standards, with proper steps and clear presentation.
4. What type of questions are covered in Class 9 maths Chapter 9 Circle Exercise 9.2?
Exercise 9.2 covers only the questions prescribed in Class 9 Maths Chapter 9 Circles, and each question is solved in the same sequence as given in NCERT.
5. Who should use the Class 9 maths Chapter 9 Circle solutions of Exercise 9.2?
The solutions of Exercise 9.2 Class 9 Maths are suitable for students who want NCERT-aligned answers for homework, practice work, and school examinations.
6. How are answers presented in Class 9 Maths Exercise 9.2 solutions?
Answers in Class 9 Maths Chapter 9 Exercise 9.2 are presented in a clean, stepwise format to help students understand the marking approach used in exams.
7. Do Class 9 maths Chapter 9 Circle solutions follow the same order as the ex 9.2 NCERT book?
Yes, the solutions strictly follow the same question numbering and order as given in NCERT Class 9 Maths Chapter 9 Circles Exercise 9.2.
8. Can Class 9 maths Chapter 9 Circle Exercise 9.2 solutions be used for school exams?
Yes, the solutions for Exercise 9.2 Class 9 Maths can be confidently used for school exams as they are fully aligned with NCERT and CBSE guidelines.
9. How is Exercise 9.2 positioned within Chapter 9 Circles?
Exercise 9.2 is an important exercise within Class 9 Maths Chapter 9 Circles, and its question formats are commonly assessed in school-level tests.
10. Why do students prefer NCERT solutions for Exercise 9.2 on Vedantu?
Students prefer NCERT solutions for Class 9 Maths Exercise 9.2 on Vedantu because they provide accurate answers, clear stepwise working, and strict alignment with the NCERT textbook.




















 Watch Video
Watch Video