NCERT Solutions for Class 9 Maths Chapter 5 Introduction To Euclids Geometry In Hindi pdf download
प्रश्नावली-5.1
1. निम्नलिखित कथनों में से कौन से कथन सत्य हैं और कौन से कथन असत्य हैं? अपने उत्तरों के लिए कारण दीजिए:
एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
उत्तर: असत्य
हम जानते हैं कि किसी भी पृष्ठ पर अनेक बिंदु हो सकते हैं, (जैसे कि \[A,\text{ }B,\text{ }C,\text{ }D\] और \[E\])। पहली अभिधारणा के अनुसार, किन्हीं दो बिंदुओं से होकर एक रेखा खींची जा सकती है।
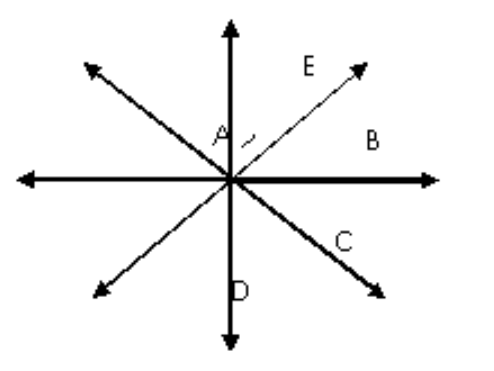
जैसा कि इस चित्र से स्पष्ट है, बिंदु \[A\] से शुरु करते हुए कई रेखाएँ खींची जा सकती हैं जैसे कि \[AB,\text{ }AC,\text{ }AD\] और \[AE\]
दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
उत्तर: असत्य
एक पन्ने पर दो बिंदु \[A\] और \[B\] बनाएँ। अब पन्ने को इस तरह से मोड़ें कि बिंदु \[A\] से होकर एक क्रीज पड़ जाए। हम जानते हैं कि एक बिंदु से होकर असंख्य रेखाएँ गुजरती हैं। इसलिए बिंदु से होकर ऐसी अनेक रेखाएँ हो सकती हैं।
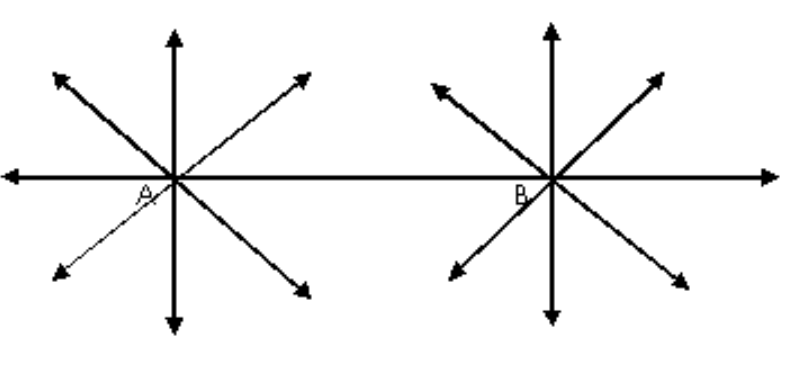
अब पन्ने को इस तरह मोड़ें कि बिंदु \[B\] से होकर एक क्रीज पड़ जाए। अब पन्ने को इस तरह से मोड़ें कि बिंदु \[A\] और \[B\] से होकर एक क्रीज पड़ जाए। हम देखते हैं कि ऐसी एक ही क्रीज संभव है। यानि दो दिए गए बिंदुओं से होकर केवल एक रेखा खींची जा सकती है।
एक सांत रेखा दोनों और अनिश्चित रूप से बढ़ाई जा सकती है।
उत्तर: सत्य
हम जानते हैं कि एक रेखा अनिश्चित लम्बाई की होती है और किसी पन्ने पर हम इसका केवल एक अंश दिखा सकते हैं।
यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
उत्तर: सत्य
यदि दो बराबर वृत्तों में से एक को दूसरे के ऊपर रखा जाए तो वे एक दूसरे को पूरी तरह ढ़क लेते हैं। ऐसा करने पर उनके केंद्र और परिधि संगत होते हैं। इससे यह सिद्ध होता है कि दोनों वृत्तों की त्रिज्याएँ बराबर होती हैं।
दी गई आकृति में यदि \[AB\text{ }=\text{ }PQ\] और \[PQ\text{ }=XY\] है, तो \[AB\text{ }=\text{ }XY\] होगा।
उत्तर: सत्य
क्योंकि, वे वस्तुएँ जो एक ही वस्तु के बराबर हों एक दूसरे के बराबर होती हैं।
2. निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
समांतर रेखाएँ, लम्ब रेखाएँ, रेखाखंड, वृत्त की त्रिज्या, वर्ग
उत्तर: दिए गए पदों को परिभाषित करने से पहले हमें इन पदों को परिभाषित करना होगा:
बिंदु: यदि हम एक पेंसिल की नोक से कागज पर निशान बनाएँ तो उस निशान को बिंदु कह सकते हैं। एक बिंदु की ना तो लम्बाई होती है और ना ही चौड़ाई। बिंदु का केवल एक स्थान होता है।
रेखा: बिंदुओं का ऐसा समूह जिसकी केवल लम्बाई होती है और कोई चौड़ाई नहीं होती है, रेखा कहलाता है। एक रेखा को दोनों दिशाओं में अनंत रूप से बढ़ाया जा सकता है।
पृष्ठ: बिंदुओं का ऐसा समूह जिसकी लम्बाई और चौड़ाई होती है लेकिन जिसकी मोटाई नहीं होती है, पृष्ठ कहलाता है।
किरण: रेखा का एक भाग जिसका सांत बिंदु होता है।
कोण: दो विभिन्न रेखाओं की किरणों का ऐसा समूह जिसका एक साझा प्रारंभिक बिंदु होता है, कोण कहलाता है।
वृत्त: एक पृष्ठ पर के उन सभी बिंदुओं का समूह जिनकी दूरी एक नियत बिंदु से बराबर होती है, वृत्त कहलाता है। नियत बिंदु को वृत्त का केंद्र कहते हैं।
चतुर्भुज: चार रेखाखंडों से बनी बंद आकृति को चतुर्भुज कहते हैं।
अब प्रश्न में दिए गए पदों की परिभाषा निम्नलिखित है:
समांतर रेखाएँ: एक ही पृष्ठ पर स्थित दो रेखाएँ जब किसी भी दिशा में अनंत रूप से बढ़ाने पर भी एक दूसरे को नहीं काटती हैं तो उन्हें समांतर रेखाएँ कहते हैं।
लम्ब रेखाएँ: यदि एक पृष्ठ पर स्थित दो रेखाएँ आपस में समकोण बनाती हैं तो उन्हें लम्ब रेखाएँ कहते हैं।
रेखाखंड: रेखा का वह भाग जिसके दो नियत बिंदु होते हैं।
त्रिज्या: वृत्त पर स्थित किसी भी बिंदु से केंद्र की दूरी को त्रिज्या कहते हैं।
वर्ग: जिस चतुर्भुज की चारों भुजाएँ बराबर हों और चारों कोण समकोण हों, उसे वर्ग कहते हैं।
3. नीचे दी हुई दो अभिधारणाओं पर विचार कीजिए:
दो भिन्न बिंदु \[\mathbf{A}\] और \[\mathbf{B}\] दिए रहने पर, एक तीसरा बिंदु \[\mathbf{C}\] ऐसा विद्यमान है जो \[\mathbf{A}\] और \[\mathbf{B}\] के बीच स्थित होता है।
यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
क्या इन अभिधारणाओं में कोई अपरिभाषित शब्द हैं? क्या ये अभिधारणाएँ अविरोधी हैं? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती हैं? स्पष्ट कीजिए।
उत्तर: हम जानते हैं कि किसी भी दो बिंदु से होकर एक रेखा गुजरती है। लेकिन यदि कोई तीसरा बिंदु दिया गया है तो उसके बारे में केवल एक ही अभिधारणा सच हो सकती है। वह बिंदु या तो उस रेखा पर स्थित होगा या उस रेखा के बाहर होगा। इसलिए बिंदु C के बारे में या तो पहला कथन सत्य होगा या फिर दूसरा।
4. यदि दो बिंदुओं \[\mathbf{A}\] और \[\mathbf{B}\] के बीच एक बिंदु \[\mathbf{C}\] ऐसा स्थित है कि \[\mathbf{AC}\text{ }=\text{ }\mathbf{BC}\] है, तो सिद्ध कीजिए कि \[\mathbf{AC}=\frac{\mathbf{1}}{\mathbf{2}}\mathbf{AB}\]है। एक आकृति खींच कर इसे स्पष्ट कीजिए।
उत्तर: दिया गया है \[AC\text{ }=\text{ }BC\] ………………..(i)
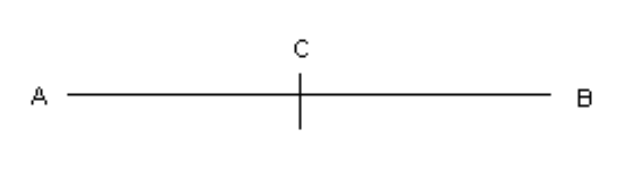
समीकरण \[(i)\]से,
\[AC\text{ }=\text{ }BC\]
या, \[AC\text{ }+\text{ }AC\text{ }=\text{ }BC\text{ }+\text{ }AC\] (दोनों तरफ \[AC\] जोड़ने पर)
या, \[2AC\text{ }=\text{ }AB\] (क्योंकि \[BC\text{ }+\text{ }AC\text{ }=\text{ }AB\])
या, \[AC=\frac{1}{2}AB\]
5. प्रश्न \[\mathbf{4}\] में, \[\mathbf{C}\] रेखाखंड \[\mathbf{AB}\] का एक मध्य-बिंदु कहलाता है। सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य बिंदु होता है।
उत्तर: दिया गया है\[,\text{ }AC\text{ }=\text{ }BC\] ……………….(i)
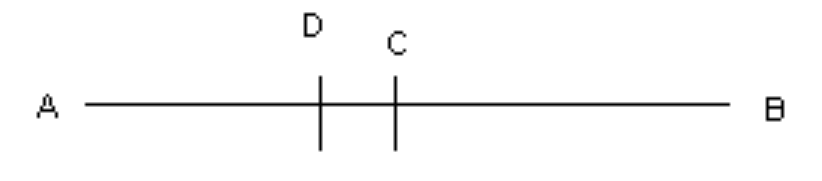
मान लीजिए कि \[AB\] का एक और मध्य बिंदु \[D\] है।
\[AD\text{ }=\text{ }DB\text{ }\ldots \ldots \ldots \ldots \ldots \ldots \ldots .\text{ }\left( ii \right)\]
समीकरण \[(i)\]से समीकरण \[(ii)\]को घटाने पर
\[AC\text{ }AD\text{ }=\text{ }BC\text{ }\text{ }DB\]
या\[,\text{ }DC\text{ }=\text{ }-DC\] (क्योंकि \[AC-AD\text{ }=\text{ }DC\] और \[CB-DB\text{ }=\text{ }-DC\])
या\[,\text{ }DC\text{ }+\text{ }DC\text{ }=\text{ }0\]
या, \[2DC\text{ }=\text{ }0\]
या, \[DC\text{ }=\text{ }0\]
इसलिए, \[C\] और \[D\] संगत होंगे
इसलिए यह सिद्ध होता है कि किसी भी रेखा का केवल एक ही मध्य बिंदु होता है।
6. दी गई आकृति में, यदि \[\mathbf{AC}\text{ }=\text{ }\mathbf{BD}\] है, तो सिद्ध कीजिए कि \[\mathbf{AB}\text{ }=\text{ }\mathbf{CD}\] है।
उत्तर: दिया गया है, \[AC\text{ }=\text{ }BD\text{ }\ldots \ldots \ldots \ldots \ldots \ldots .\left( i \right)\]
\[AC\text{ }=\text{ }AB\text{ }+\text{ }BC\text{ }\ldots \ldots \text{ }\left( ii \right)\]
और, \[BD\text{ }=\text{ }BC\text{ }+\text{ }CD\text{ }\ldots \ldots \text{ }\left( iii \right)\]
समीकरण \[(i)\]में समीकरण \[(ii)\]और \[(iii)\]का मान रखने पर
\[\begin{array}{*{35}{l}} AB\text{ }+\text{ }BC\text{ }=\text{ }BC\text{ }+\text{ }C \\ AB\text{ }+\text{ }BC\text{ }\text{ }BC\text{ }=\text{ }CD \\ AB\text{ }=\text{ }CD \\ \end{array}\]
इसलिए, \[AB\text{ }=\text{ }CD\]
7. यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना जाता है? (ध्यान दीजिए कि यह प्रश्न पाँचवीं अभिधारणा से संबंधित नहीं है।)
उत्तर: यह अभिगृहीत विश्व के किसी भी हिस्से में हमेशा सही साबित होता है, इसलिए इसे सर्वव्यापी सत्य माना जाता है।
प्रश्नावली5.2
1. आप यूक्लिड की पाँचवीं अभिधारणा को किस प्रकार लिखेंगे ताकि वह सरलता से समझी जा सके?
उत्तर: यूक्लिड की पाँचवीं अभिधारण को इस तरह से लिखा जा सकता है:
बिंदु \[P\] से होकर जाने वाली रेखा \[l\] के समांतर होती है।
ऐसी केवल एक ही रेखा संभव है।
2. क्या यूक्लिड की पाँचवीं अभिधारणा से समांतर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है? स्पष्ट कीजिए।
उत्तर: यदि कोई रेखा \[l\] दो रेखाओं \[m\] और \[n\] से इस तरह गुजरती है कि इसके एक तरफ के अंत:कोणों का योग दो समकोणों के बराबर होता है, तो यूक्लिड की पाँचवीं अभिधारणा के अनुसार दोनों रेखाएँ (\[m\] और \[n\]) उस तरफ आपस में नहीं मिलती हैं। हम यह भी जानते हैं कि रेखा l की दूसरी ओर बने अंत:कोणों का योग भी दो समकोण होगा। इसलिए दोनों रेखाएँ (\[m\] और \[n\] दूसरी तरफ भी आपस में नहीं मिलेंगी। चूँकि ये रेखाएँ आपस में कभी नहीं मिलेंगी, इसलिए ये समांतर हैं।
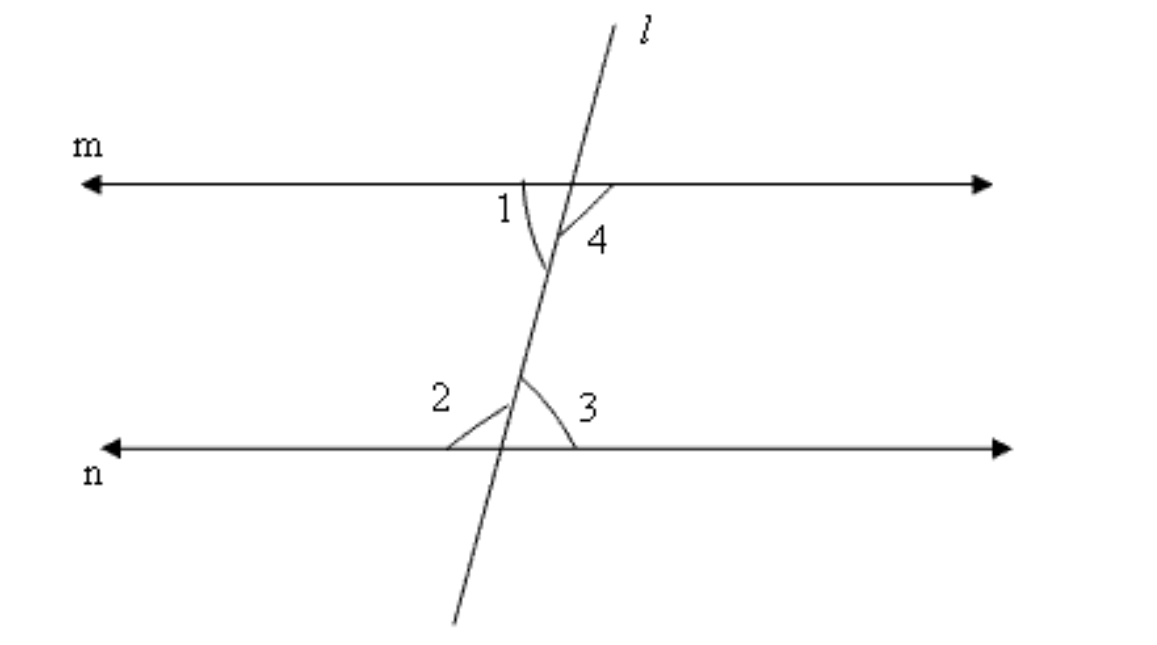
\[m\text{ }||\text{ }n\], यदि\[,\angle 1\text{ }+\angle 2\text{ }=\text{ }180{}^\circ \] (दो समकोण)
या, \[\angle 3\text{ }+\angle 4\text{ }=\text{ }180{}^\circ \]
NCERT Solutions for Class 9 Maths Chapter 5 Introduction To Euclid's Geometry In Hindi
Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 9 Maths Chapter 5 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 9 Maths Chapter 5 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.
NCERT Solutions for Class 9 Maths Chapter 5 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 9 Maths Introduction to Euclids Geometry solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that.
NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 9 Maths Introduction to Euclids Geometry in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 9 can download these solutions at any time as per their convenience for self-study purpose.
These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 9 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.
