NCERT Solutions for Class 9 Maths Chapter 7 - Triangles

• Exercise 7.1: This exercise comprises eight questions, and it mainly deals with the basic properties of triangles such as interior angles, exterior angles, and inequalities. The questions are mostly objective and require students to apply simple formulas to find the values of angles and sides of triangles.

• Exercise 7.2: This exercise consists of eight questions and mainly focuses on the congruence of triangles. The questions in this exercise deal with the criteria for congruence of triangles such as SSS, SAS, ASA, RHS, and AAS. The questions require students to apply these criteria to determine if the given triangles are congruent or not.

• Exercise 7.3: This exercise comprises five questions, and it deals with the properties of isosceles and equilateral triangles. The questions in this exercise require students to apply the properties of these triangles to find the values of angles and sides.

Access NCERT Answers for Class-9 Maths Chapter 7 – Triangles

Exercise-7.1

1. In quadrilateral ACBD, AC = AD and AB bisects $$\mathrm{\angle }A$$ (See the given figure). Show that $$\mathrm{\Delta }ABC\cong \mathrm{\Delta }ABD$$. What can you say about BC and BD?

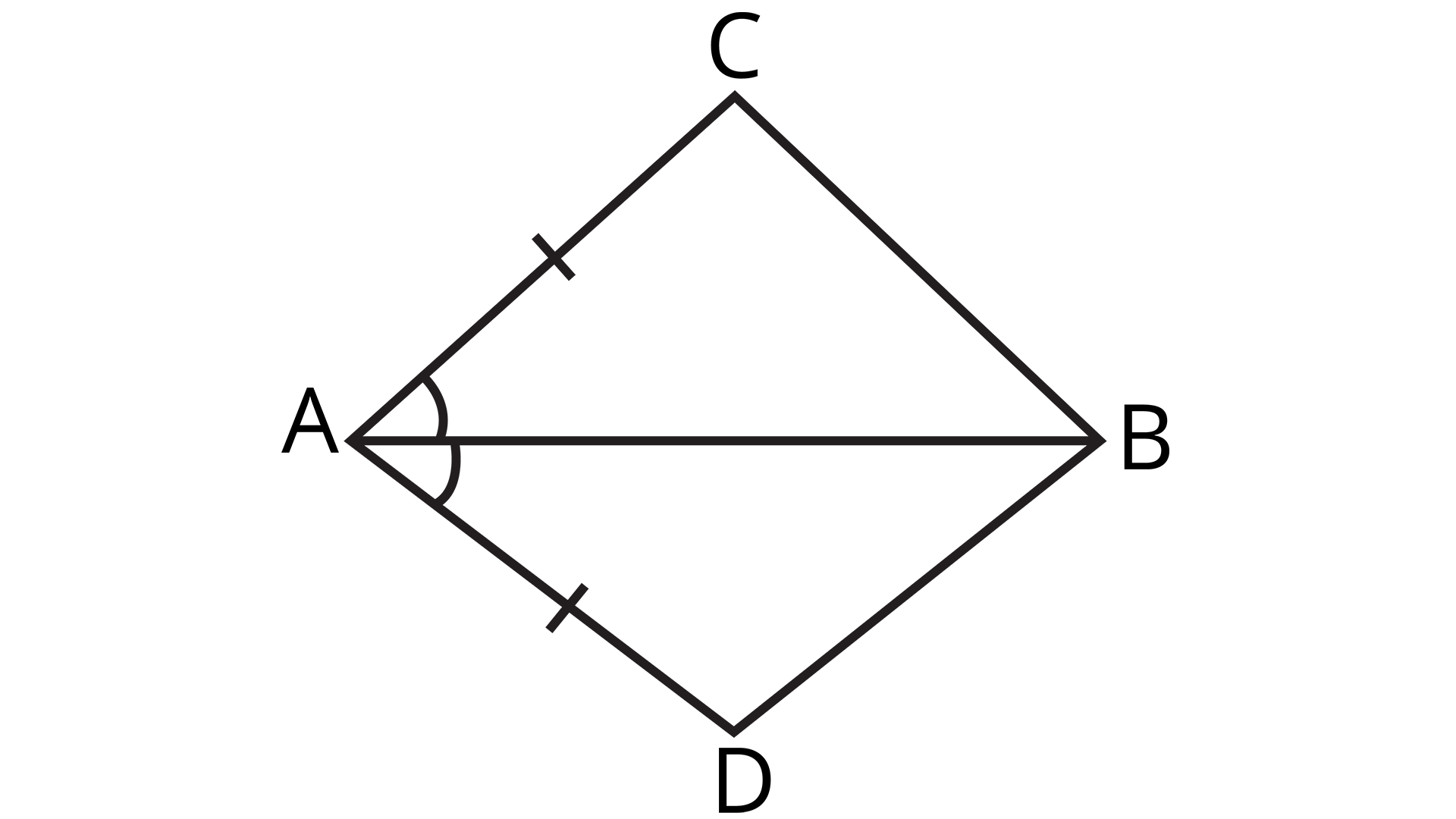
Quadrilateral ABCD 

Ans: Given: In quadrilateral ACBD, AC = AD and AB is bisected by $$\mathrm{\angle }A$$

To find: Show that $$\mathrm{\Delta }ABC\cong \mathrm{\Delta }ABD$$. 

In $$\mathrm{\Delta }ABC\text{ , }\mathrm{\Delta }ABD$$

$$AC=AD$$ (Given)

$$\mathrm{\angle }CAB=\mathrm{\angle }DAB$$     (AB bisects ∠A)

$$AB=AB$$        (Common)

$$\therefore \mathrm{\Delta }ABC\cong \mathrm{\Delta }ABD$$            (By SAS congruence rule)

$$\therefore BC=BD$$     (By CPCT)

Therefore, BC and BD are of equal lengths.

2. ABCD is a quadrilateral in which AD = BC and $$\mathrm{\angle }DAB=\mathrm{\angle }CBA$$  (See the given figure). Prove that

(i)  $$\mathrm{\Delta }ABD\cong \mathrm{\Delta }BAC$$

(ii) BD = AC

(iii)$$\mathrm{\angle }ABD=\mathrm{\angle }BAC$$.

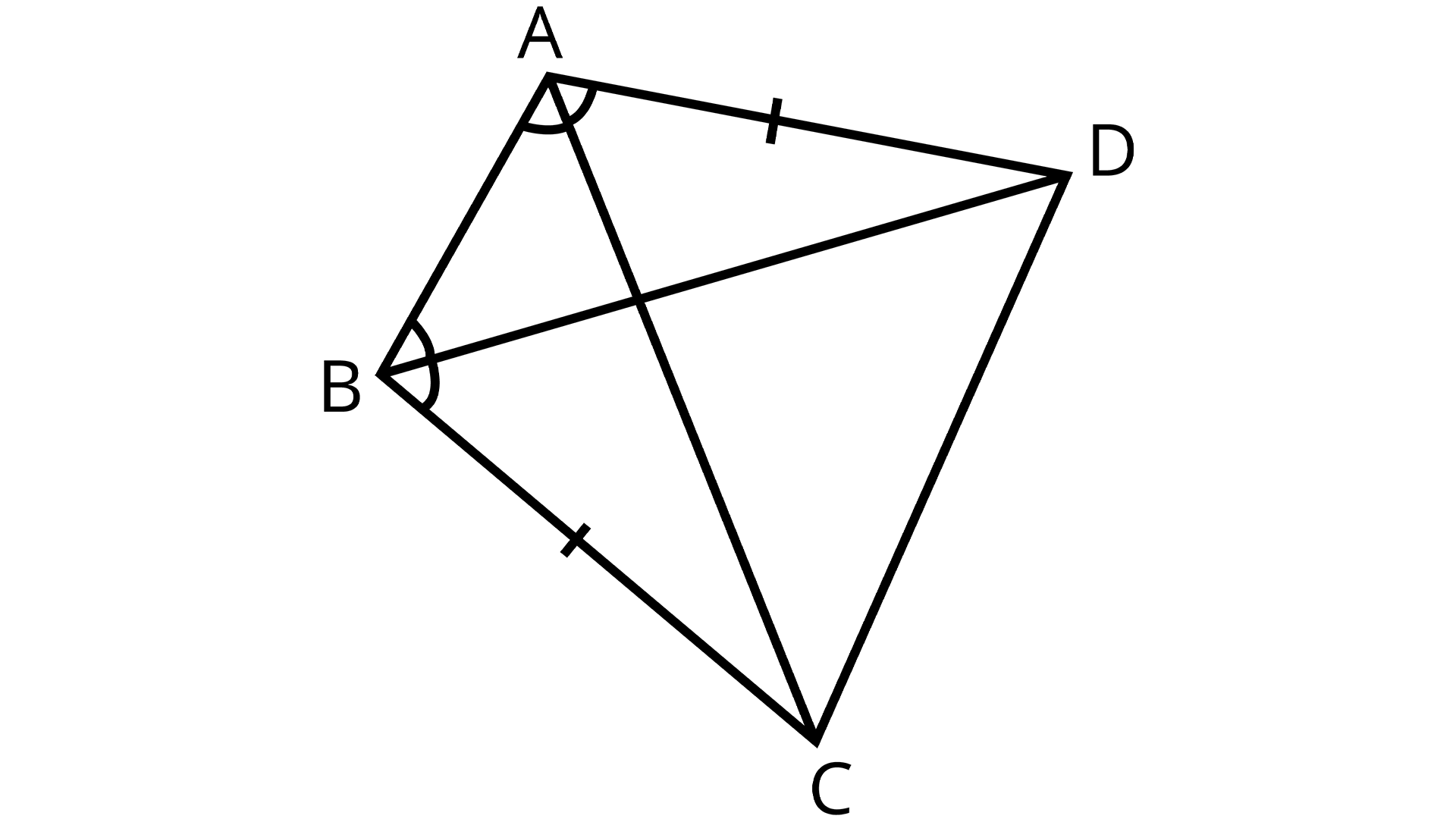
Quadrilateral ABCD with AD = BC

Ans : Given: ABCD is a quadrilateral where AD = BC and $$\mathrm{\angle }DAB=\mathrm{\angle }CBA$$

To prove: 

(i)  $$\mathrm{\Delta }ABD\cong \mathrm{\Delta }BAC$$

(ii) BD = AC

(iii)$$\mathrm{\angle }ABD=\mathrm{\angle }BAC$$.

In $$\mathrm{\Delta }ABD\text{ , }\mathrm{\Delta }BAC$$,

AD = BC    (Given)

$$\mathrm{\angle }DAB=\mathrm{\angle }CBA$$   (Given)

AB = BA     (Common)

$$\therefore \mathrm{\Delta }ABD\cong \mathrm{\Delta }BAC$$              (By SAS congruence rule)

$$\therefore BD=AC$$          (By CPCT)

And, $$\mathrm{\angle }ABD=\mathrm{\angle }BAC$$           (By CPCT)

3. AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

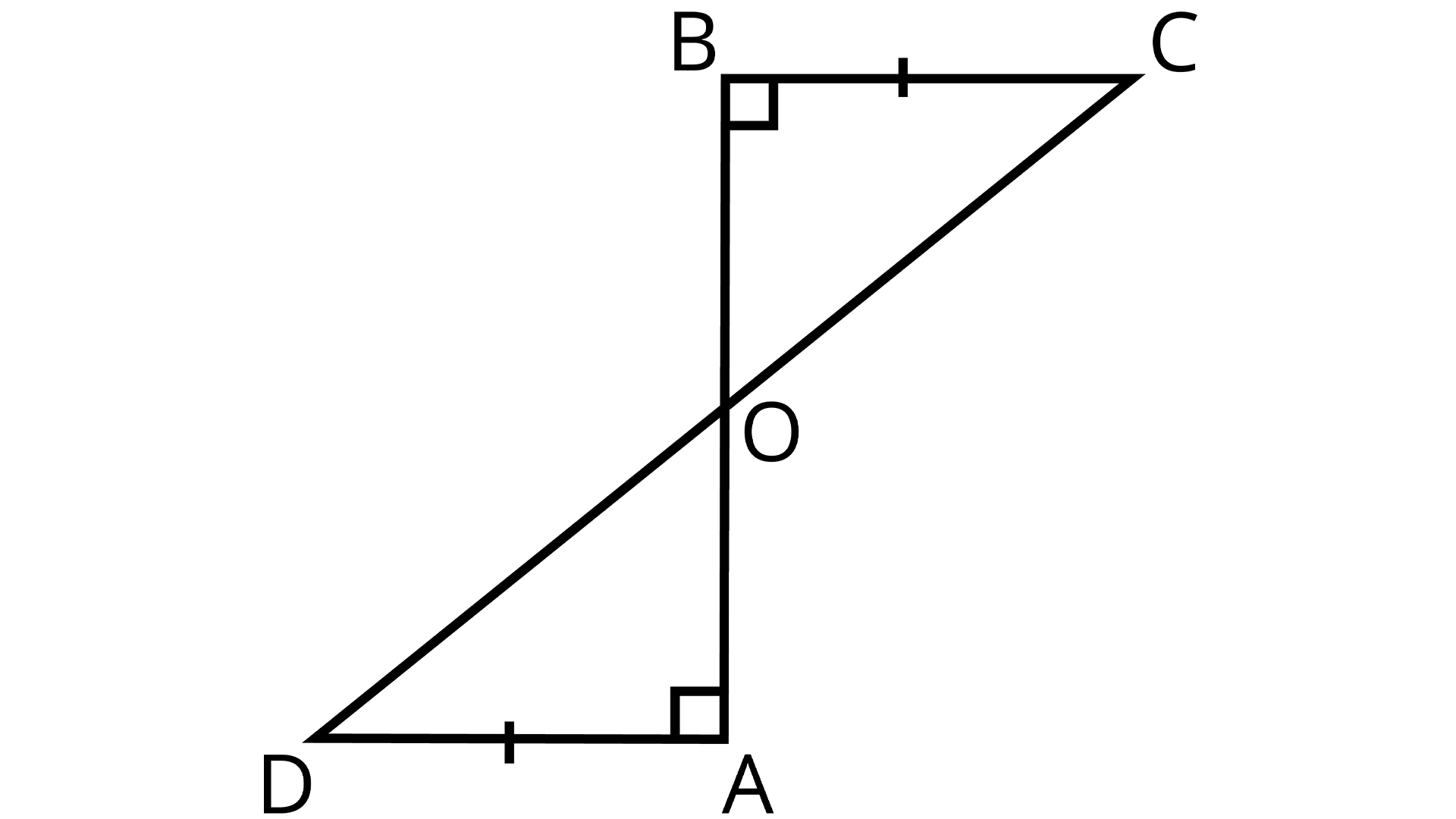
Figure showing AD and BC equal perpendiculars to a line segment AB

Ans: Given: AD and BC are equal perpendiculars to a line segment AB 

To prove: CD bisects AB.

In $$\mathrm{\Delta }BOC\text{ , }\mathrm{\Delta }AOD$$,

$$\mathrm{\angle }BOC=\mathrm{\angle }AOD$$     (Vertically opposite angles)

$$\mathrm{\angle }CBO=\mathrm{\angle }DAO$$        (Each right angle )

BC = AD     (Given)

$$\therefore \mathrm{\Delta }BOC\cong \mathrm{\Delta }AOD$$     (AAS congruence rule)

$$\therefore BO=AO$$     (By CPCT)

$$\Rightarrow$$CD bisects AB.

4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that $$\mathrm{\Delta }ABC\cong \mathrm{\Delta }CDA$$.

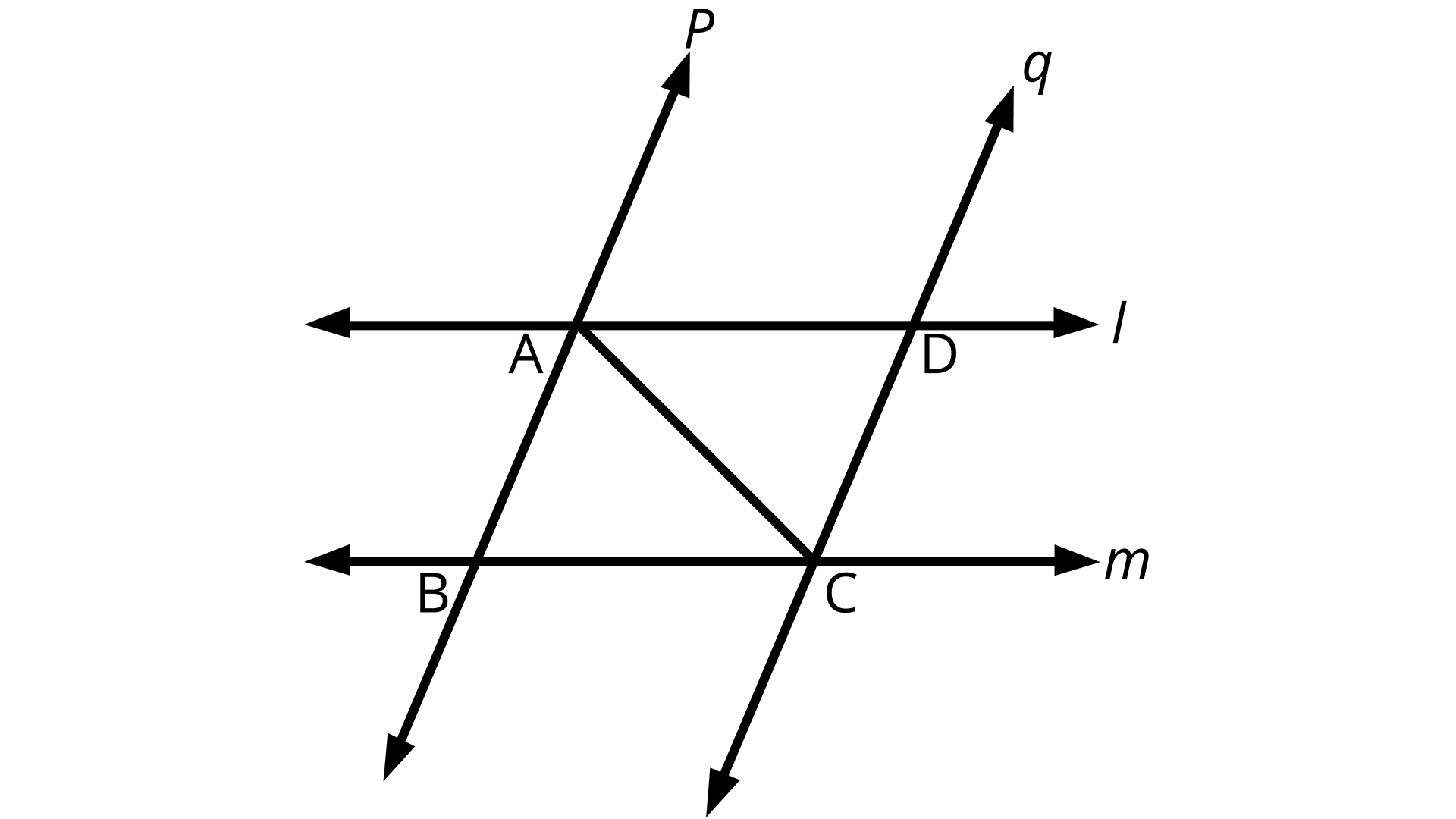
Two  Parallel Lines L and M 

Given: l and m are two parallel lines intersected by another pair of parallel lines p and q To prove:  $$\mathrm{\Delta }ABC\cong \mathrm{\Delta }CDA$$.

In $$\mathrm{\Delta }ABC\text{ , }\mathrm{\Delta }CDA$$,

$$\mathrm{\angle }BAC=\mathrm{\angle }DCA$$       (Alternate interior angles, as$$p||q$$)

2AC = CA     (Common)

$$\mathrm{\angle }BCA=\mathrm{\angle }DAC$$       (Alternate interior angles, as $$l||m$$)

$$\therefore \mathrm{\Delta }ABC\cong \mathrm{\Delta }CDA$$          (By ASA congruence rule)

5. Line l is the bisector of an angle $$\mathrm{\angle }A$$ and B is any point on l. BP and BQ are $$perpendiculars from B to the arms of $$\mathrm{\angle }A$$ (see the given figure). Show that:

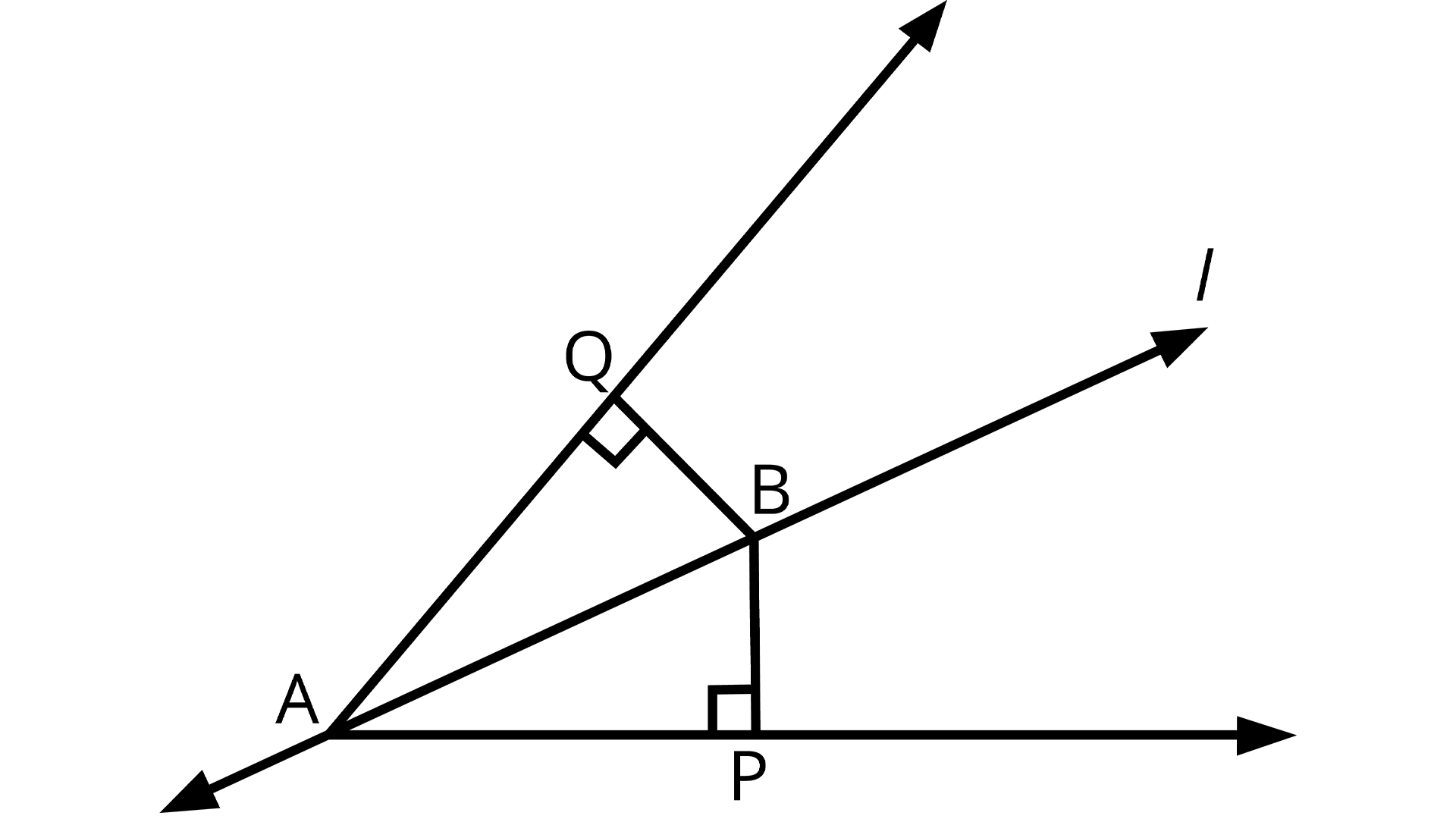
Line l the Bisector of an Angle A

(i) $$\mathrm{\Delta }APB\cong \mathrm{\Delta }AQB$$

(ii) BP = BQ or B is equidistant from the arms of ∠A.

Ans: Given: Line l is the bisector of an angle $$\mathrm{\angle }A$$ and B is any point on l.

To prove: (i) $$\mathrm{\Delta }APB\cong \mathrm{\Delta }AQB$$

(ii) $$BP=BQ$$ or B is equidistant from the arms of $$\mathrm{\angle }A$$.

In $$\mathrm{\Delta }APB\text{ , }\mathrm{\Delta }AQB$$,

$$\mathrm{\angle }APB=\mathrm{\angle }AQB$$        (Each right angle )

$$\mathrm{\angle }PAB=\mathrm{\angle }QAB$$      (l is the angle bisector of $$\mathrm{\angle }A$$)

AB = AB (Common)

$$\therefore \mathrm{\Delta }APB\cong \mathrm{\Delta }AQB$$       (By AAS congruence rule)

$$\therefore BP=BQ$$        (By CPCT)

Or, it can be said that B is equidistant from the arms of $$\mathrm{\angle }A$$.

6. In the given figure, $$AC=AE,AB=AD$$ and $$\mathrm{\angle }BAD=\mathrm{\angle }EAC$$. Show that BC = DE.

Ans:

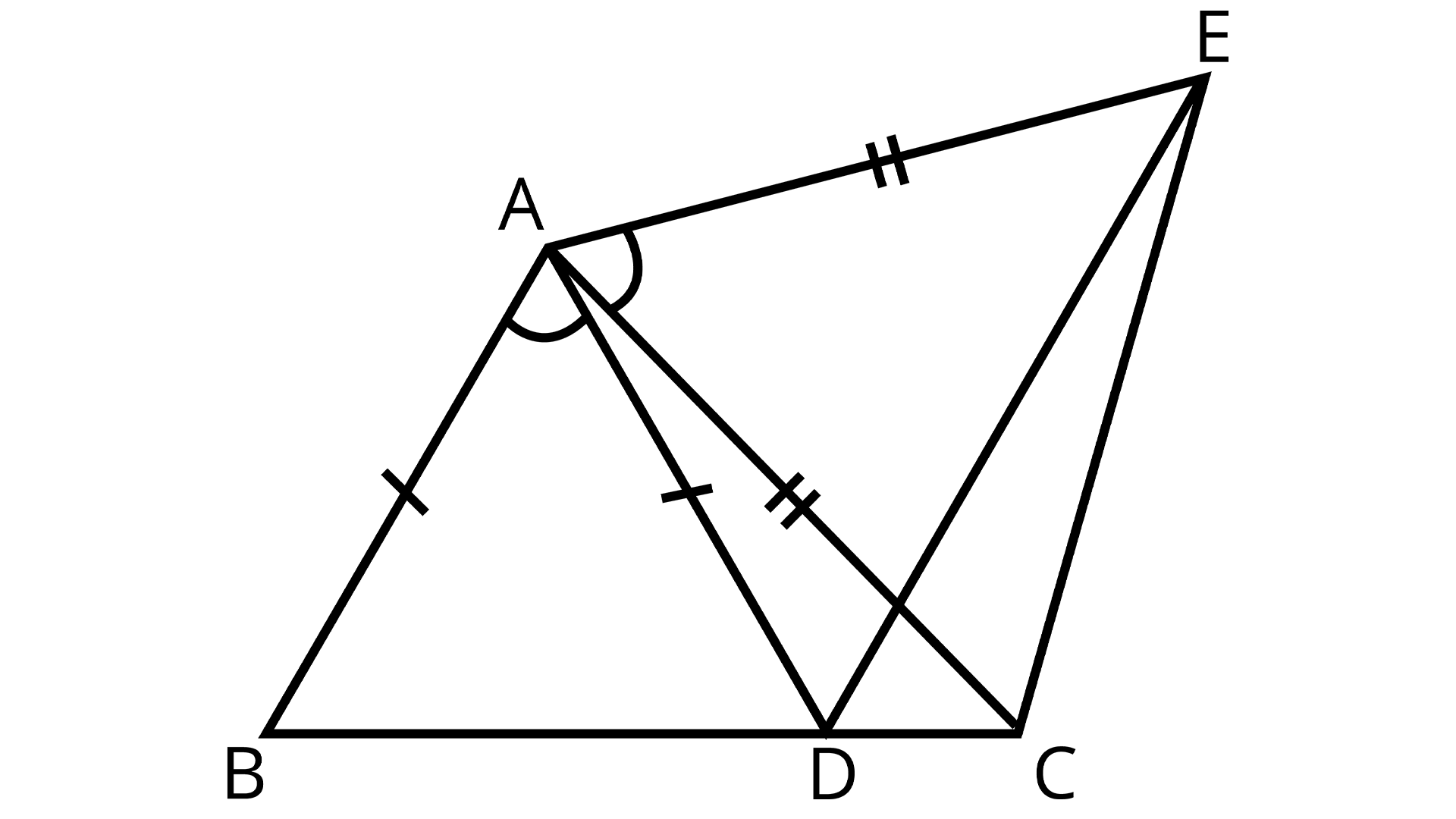
Angle BAD = angle EAC

Given: $$\mathrm{\angle }BAD=\mathrm{\angle }EAC$$

To prove: BC = DE

It is given that $$\mathrm{\angle }BAD=\mathrm{\angle }EAC$$

$$\mathrm{\angle }BAD+\mathrm{\angle }DAC=\mathrm{\angle }EAC+\mathrm{\angle }DAC$$

$$\mathrm{\angle }BAC=\mathrm{\angle }DAE$$

In $$\mathrm{\Delta }BAC\text{ , }\mathrm{\Delta }DAE$$,

AB = AD     (Given)

$$\mathrm{\angle }BAC=\mathrm{\angle }DAE$$      (Proved above)

AC = AE    (Given)

$$\therefore \mathrm{\Delta }BAC\cong \mathrm{\Delta }DAE$$       (By SAS congruence rule)

$$\therefore BC=DE$$           (By CPCT)

7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that $$\mathrm{\angle }BAD=\mathrm{\angle }ABE$$ and $$\mathrm{\angle }EPA=\mathrm{\angle }DPB$$ (See the given figure). Show that

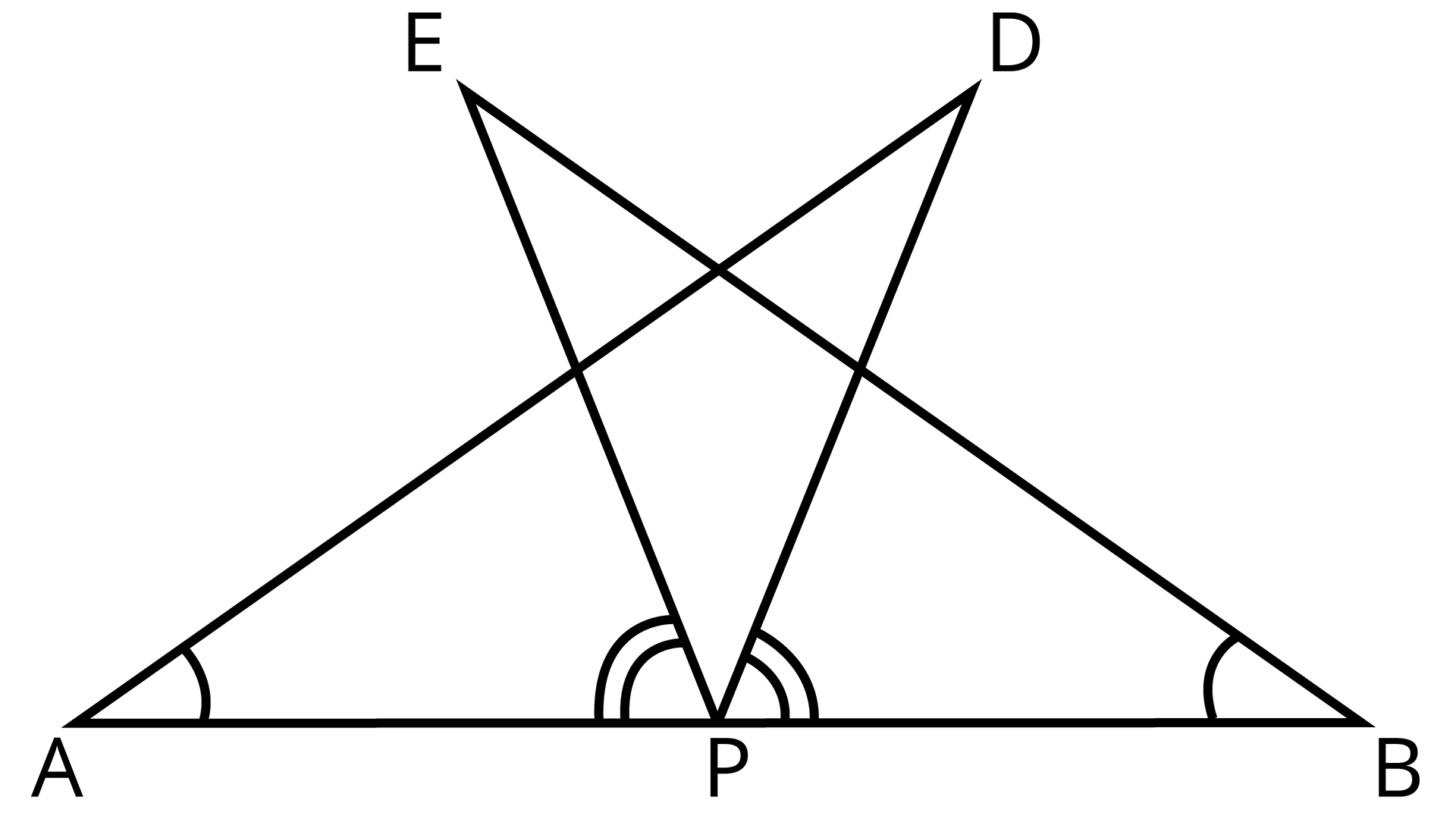
Line segment AB with its mid point P

(i) $$\mathrm{\Delta }DAP\cong \mathrm{\Delta }EBP$$

(ii) AD = BE

Ans: Given: AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that $$\mathrm{\angle }BAD=\mathrm{\angle }ABE$$ and $$\mathrm{\angle }EPA=\mathrm{\angle }DPB$$

To prove: (i) $$\mathrm{\Delta }DAP\cong \mathrm{\Delta }EBP$$

(ii) AD = BE

It is given that $$\mathrm{\angle }EPA=\mathrm{\angle }DPB$$

$$\mathrm{\angle }EPA+\mathrm{\angle }DPE=\mathrm{\angle }DPB+\mathrm{\angle }DPE$$

$$\therefore \mathrm{\angle }DPA=\mathrm{\angle }EPB$$

In $$\mathrm{\Delta }DAP\text{ , }\mathrm{\Delta }EBP$$,

$$\mathrm{\angle }DAP=\mathrm{\angle }EBP$$ (Given)

AP = BP        (P is mid-point of AB)

$$\mathrm{\angle }DPA=\mathrm{\angle }EPB$$   (From above)

$$\therefore \mathrm{\Delta }DAP\cong \mathrm{\Delta }EBP$$    (ASA congruence rule)

$$\therefore AD=BE$$          (By CPCT)

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:

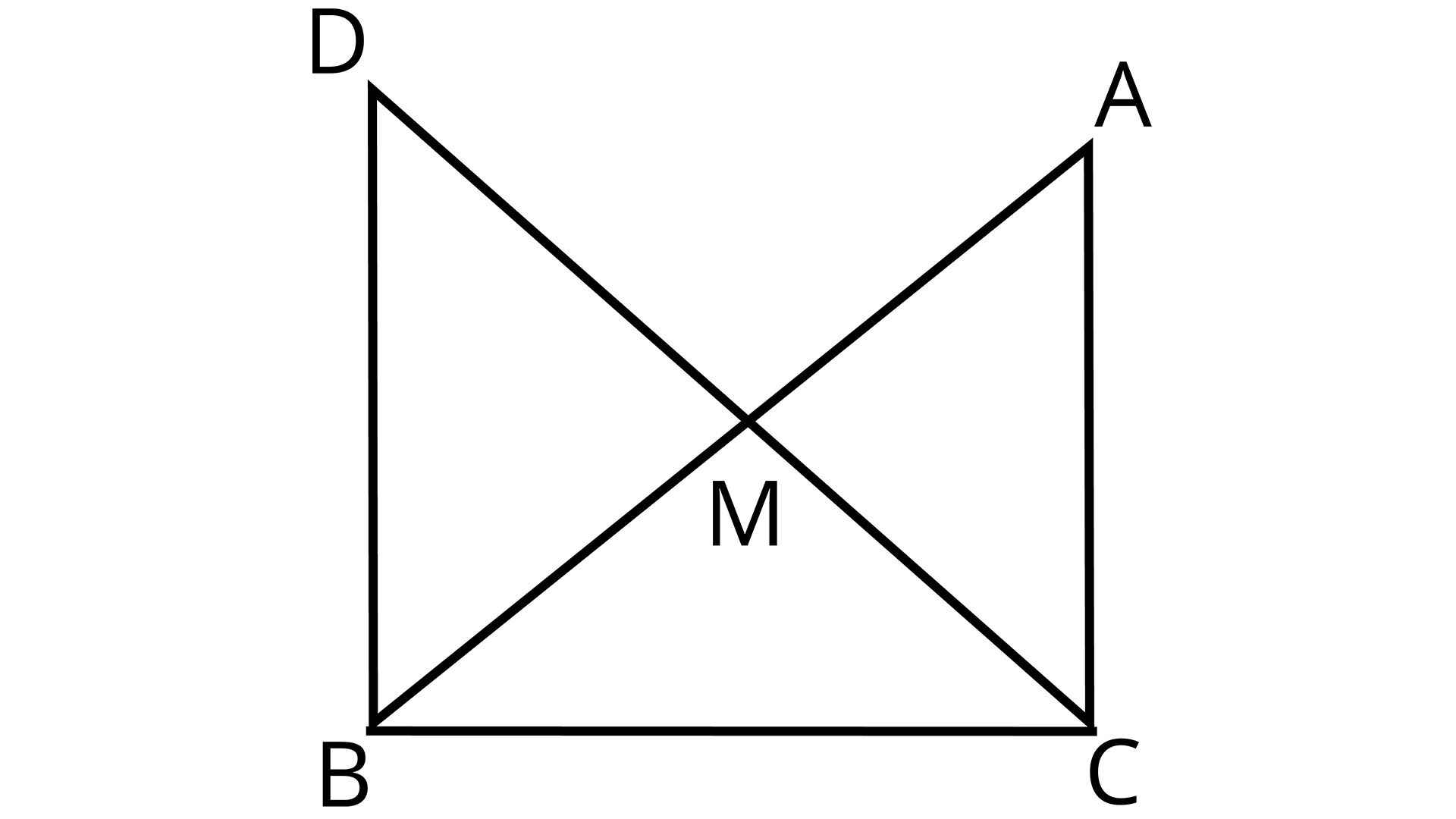
Triangle ABC right - angled at C and midpoint M of AB

i) $$\mathrm{\Delta }AMC\cong \mathrm{\Delta }BMD$$

ii) $$\mathrm{\angle }DBC$$ is a right angle.

iii) $$\mathrm{\Delta }DBC\cong \mathrm{\Delta }ACB$$

iv) $$CM={\displaystyle \frac{1}{2}}AB$$

Ans: Given: M is the mid-point of hypotenuse AB. DM = CM

(i) In $$\mathrm{\Delta }AMC,\mathrm{\Delta }BMD$$,

AM = BM (M is the mid-point of AB)

$$\mathrm{\angle }AMC=\mathrm{\angle }BMD$$        (Vertically opposite angles)

CM = DM          (Given)

$$\therefore \mathrm{\Delta }AMC\cong \mathrm{\Delta }BMD$$          (By SAS congruence rule)

$$\therefore AC=BD$$ (By CPCT)

And, $$\mathrm{\angle }ACM=\mathrm{\angle }BDM$$(By CPCT)

(ii) $$\mathrm{\angle }ACM=\mathrm{\angle }BDM$$

However,  $$\mathrm{\angle }ACM\text{ , }\mathrm{\angle }BDM$$ are alternate interior angles.

Since alternate angles are equal,

It can be said that $$DB||AC$$

(Co-interior angles)

(iii) In $$\mathrm{\Delta }DBC\text{ , }\mathrm{\Delta }ACB$$,

DB = AC      (Already proved)

$$\mathrm{\angle }DBC=\mathrm{\angle }ACB$$          (Each $${90}^o$$)

BC = CB (Common)

$$\therefore \mathrm{\Delta }DBC\cong \mathrm{\Delta }ACB$$           (SAS congruence rule)

(iv) $$\therefore \mathrm{\Delta }DBC\cong \mathrm{\Delta }ACB$$

AB = DC (By CPCT)

AB = 2 CM

$$CM={\displaystyle \frac{1}{2}}AB$$

Exercise (7.2)

1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that: 

(i) OB = OC (ii) AO bisects ∠A

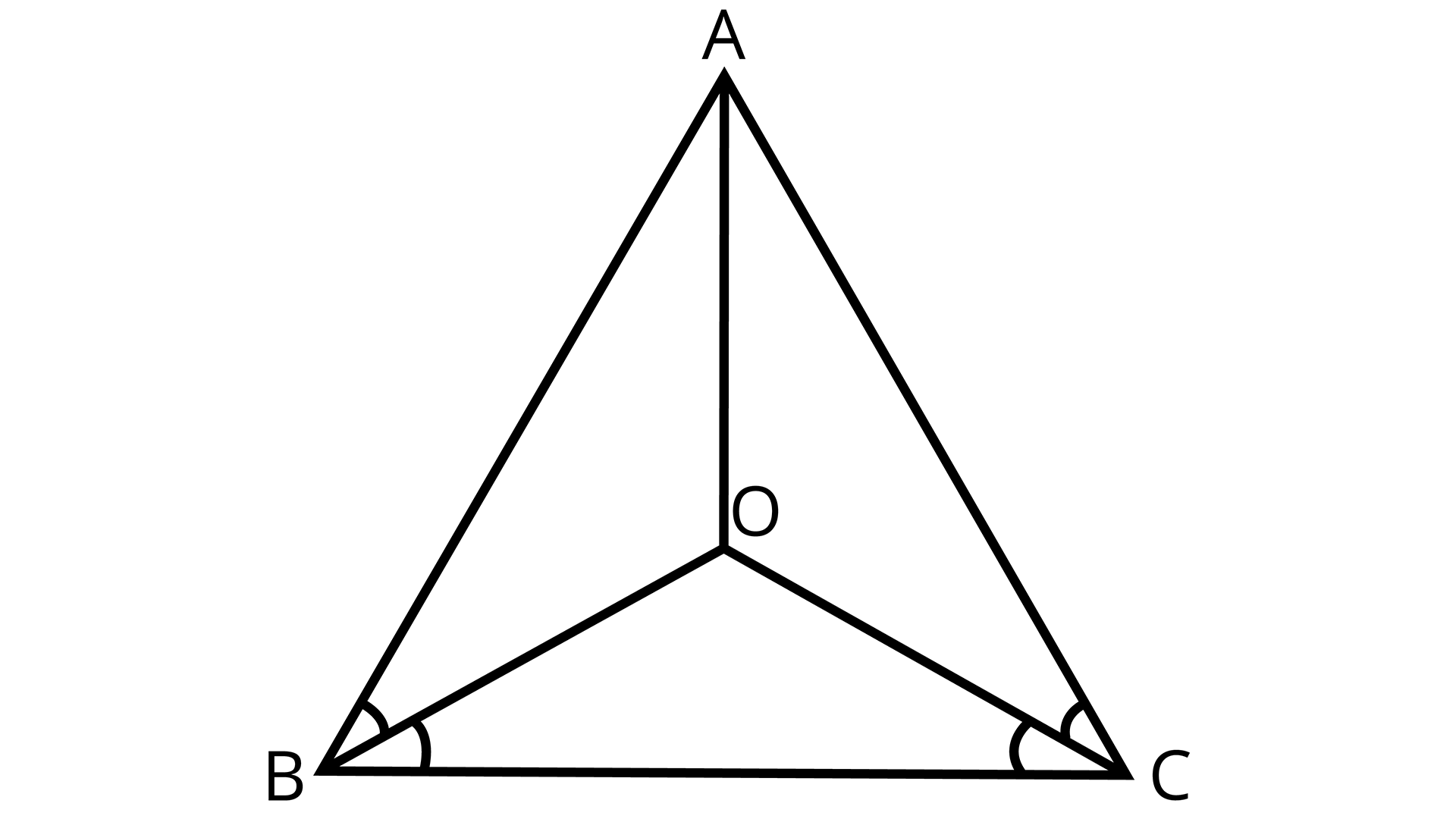
Isosceles triangle with AB = AC

Ans: We know, $\mathrm{\angle }ABC=\mathrm{\angle }ACB$ $\text{[Equal angles of isosceles triangle]}$

$\Rightarrow {\displaystyle \frac{1}{2}}\mathrm{\angle }ABC={\displaystyle \frac{1}{2}}ACB$

$\Rightarrow \mathrm{\angle }OBC=\mathrm{\angle }OCB$

$\therefore OB=OC$ $\text{[Sides opposite to equal angles of Isosceles triangle are equal]}$

Now, In $\mathrm{\Delta }ABO$ and $\mathrm{\Delta }ACO$,

$AB=AC$ $\text{[Equal sides of Isosceles triangle]}$

$OB=OC$ $\text{[Proved above]}$

AO=AO (Common)

$\therefore \mathrm{\Delta }ABO\cong \mathrm{\Delta }ACO$ $\text{[By SSS]}$

$\therefore \mathrm{\angle }BAO=\mathrm{\angle }CAO$ $\text{[CPCT]}$

$\therefore$ AO bisects angle A.

2. In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.

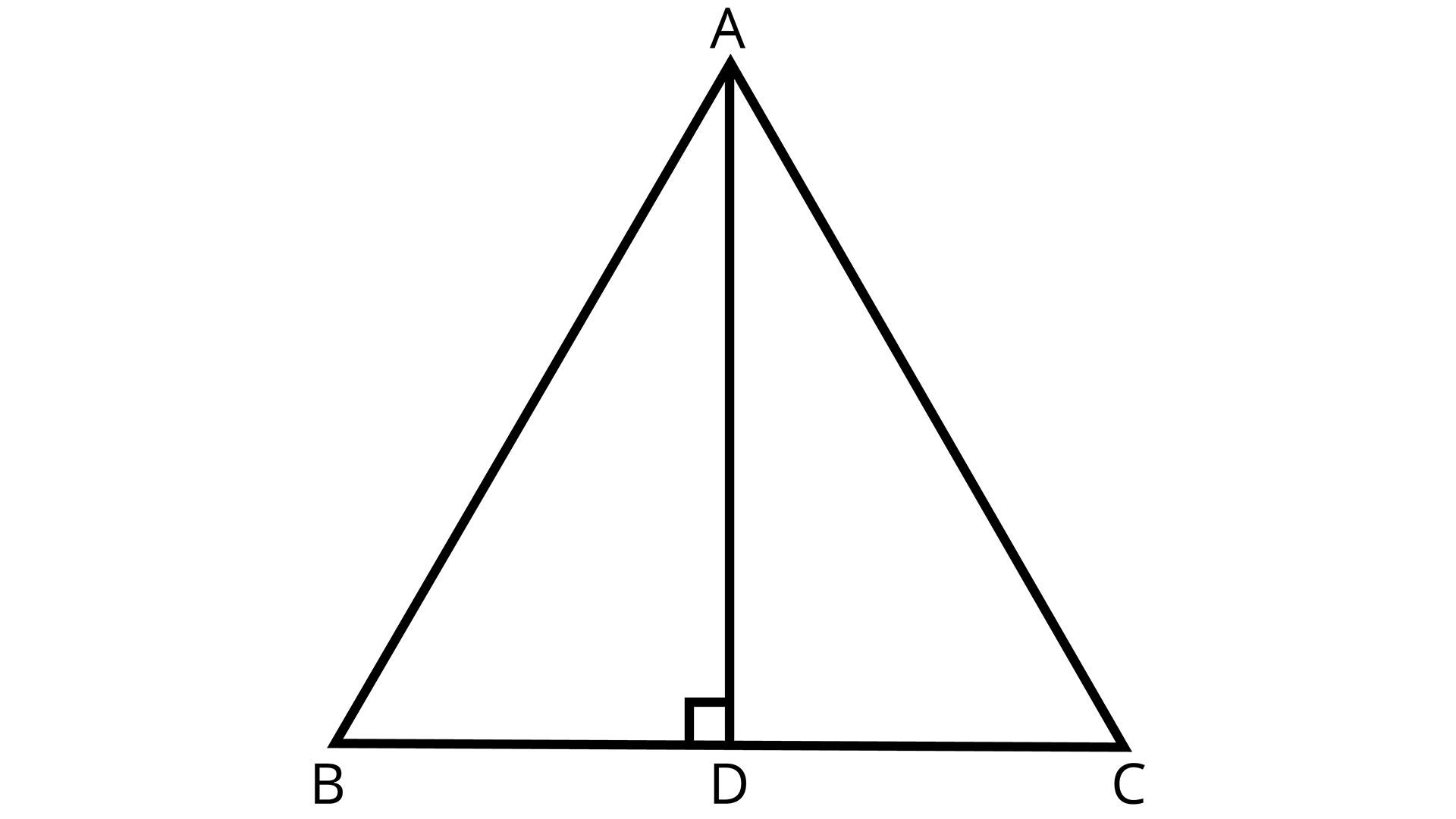
Triangle ABC , AD being the bisector of BC 

Ans: $\because$ AD is perpendicular bisector of BC,

$\therefore$$BD=DC$

& $\mathrm{\angle }ADB=\mathrm{\angle }ADC$ $\text{[Each 90°]}$

Now, in$\mathrm{\Delta }ABD$ and $\mathrm{\Delta }ACD$,

$AD=AD$ (Common)

$\mathrm{\angle }ADB=\mathrm{\angle }ADC$ $\text{[Proved above]}$ $BD=CD$ $\text{[Proved above]}$

$\therefore \mathrm{\Delta }ADB\cong \mathrm{\Delta }ACD$ $\text{[by SAS]}$

$\therefore AB=AC$ (CPCT)

So, $\mathrm{\Delta }ABC$ is an isosceles triangle with $$AB=AC$$

3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.

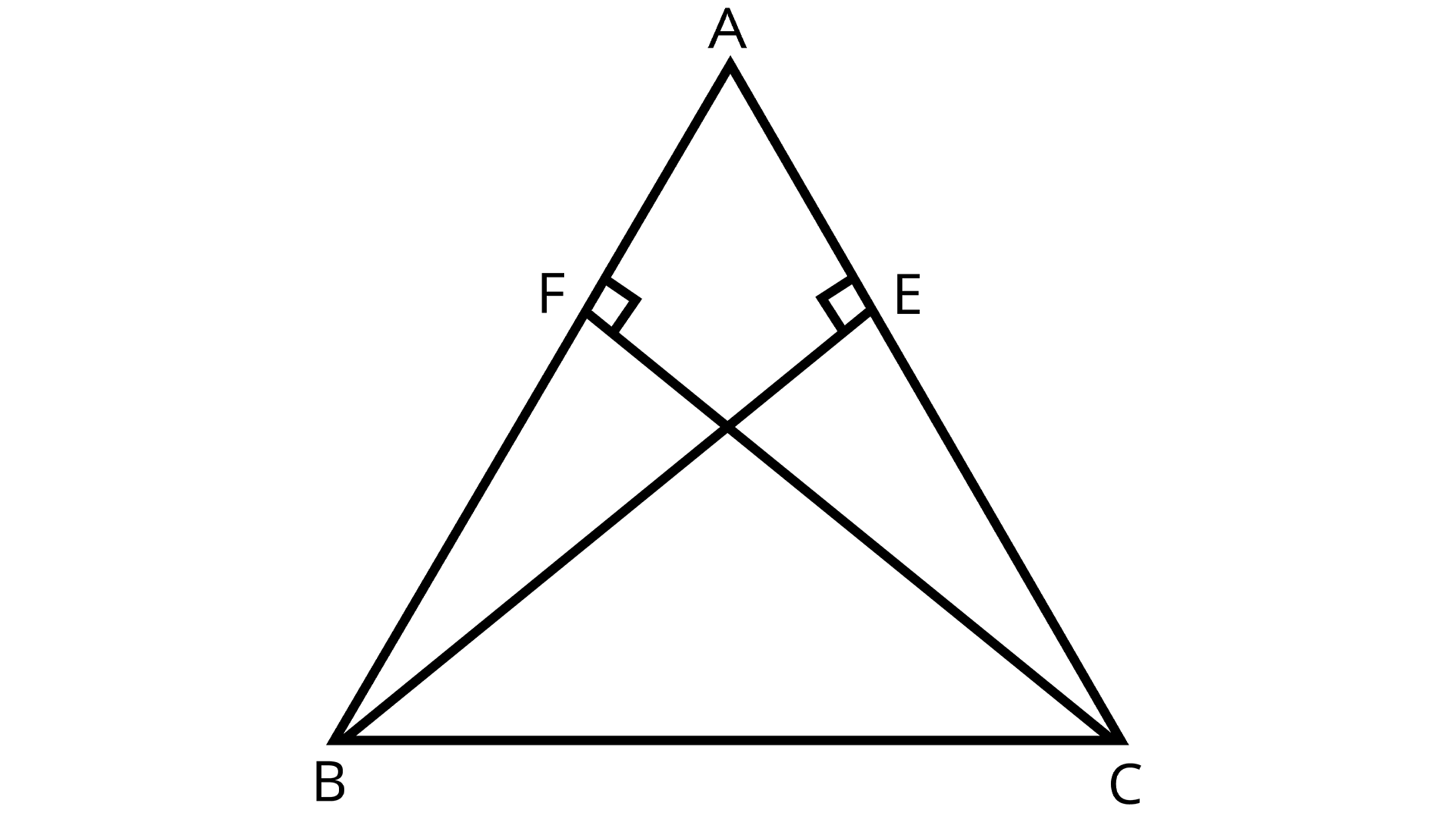
Isosceles triangle ABC

Ans: In $\mathrm{\Delta }ABE$and $\mathrm{\Delta }ACF$,

$\mathrm{\angle }AEB=\mathrm{\angle }AFE$ $\text{[Each 90°]}$

$\mathrm{\angle }BAE=\mathrm{\angle }CAF$ (Common)

$AB=AC$ [Given]

$\therefore \mathrm{\Delta }ABE\cong \mathrm{\Delta }ACF$ $\text{[By AAS]}$

$\therefore BE=CF$ (CPCT)

4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that

(i) $$\mathrm{\Delta }ABE\cong \mathrm{\Delta }ACF$$

(ii) AB = AC i.e., ABC is an isosceles triangle

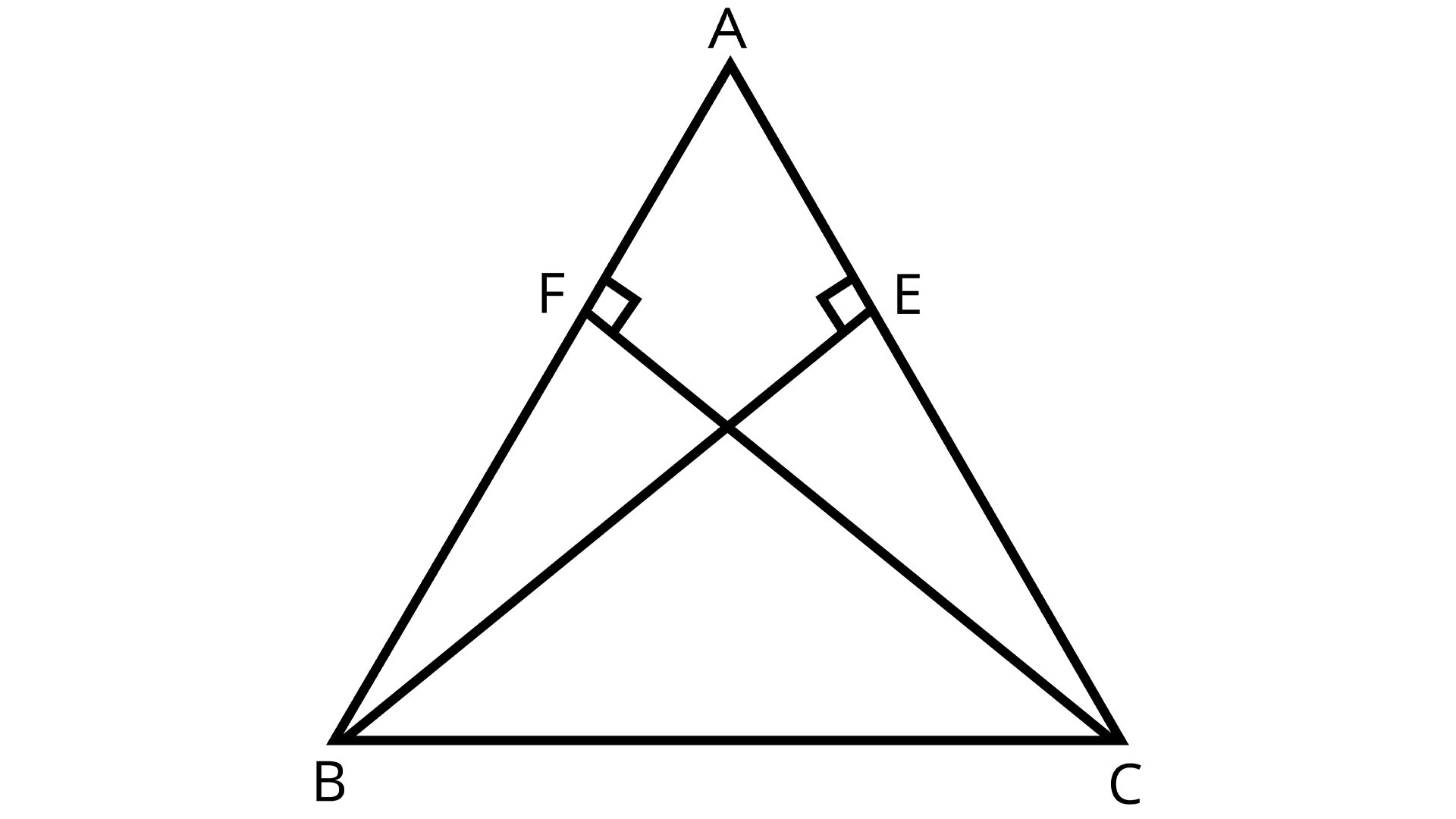
Triangle ABC with equal altitudes

Ans: In $\mathrm{\Delta }ABE$and $\mathrm{\Delta }ACF$,

$$\mathrm{\angle }BAE=\mathrm{\angle }CAF$$ (Common)

$\mathrm{\angle }BEA=\mathrm{\angle }CFA$               $\text{[Each 90°]}$

$BE=CF$ [Given]

$\therefore \mathrm{\Delta }ABE\cong \mathrm{\Delta }ACF$ $\text{[by AAS]}$

$\therefore AB=AC$ (CPCT)

And therefore, $\mathrm{\Delta }ABC$ is an isosceles triangle with AB=AC.

5. ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.

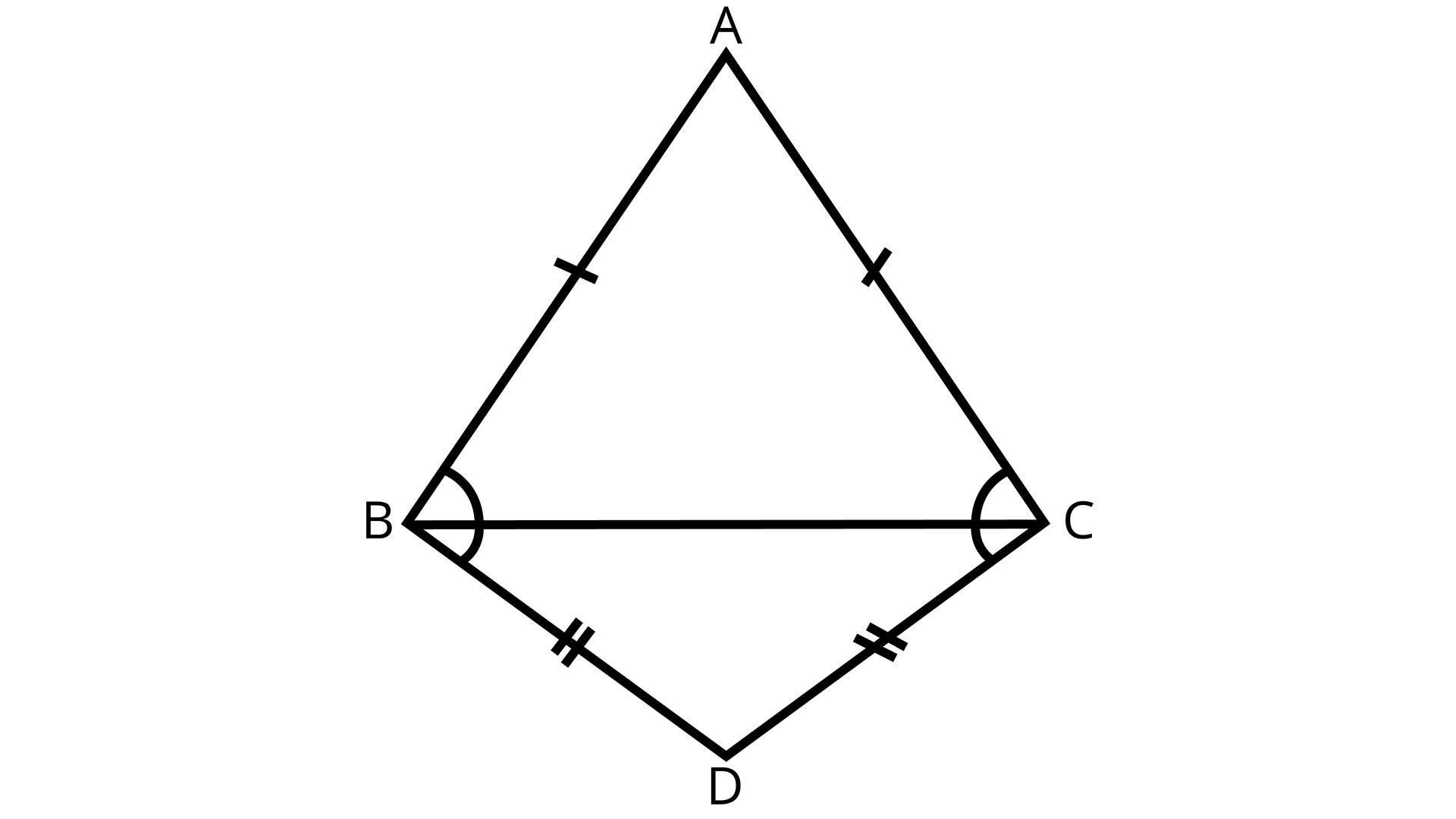
Two Isosceles Triangles

Ans: Since AB=AC, and DB=DC,

$\therefore$ABDC is a quadrilateral with adjacent sides being equal.

$\Rightarrow$ABDC is a kite.

We know that one pair of opposite (obtuse) angles of kite are equal.

Hence, $\mathrm{\angle }ABD=\mathrm{\angle }ACD$

6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.

Isosceles Triangle in which AB = AC

Ans: In $\mathrm{\Delta }ABC$

$\mathrm{\angle }ABC=\mathrm{\angle }ACB$ $\text{[angles opposite to equal sides of a triangle]}$ … (1)

Similarly, in $\mathrm{\Delta }ADC$

$\mathrm{\angle }ADC=\mathrm{\angle }ACD$ $\text{[angles opposite to equal sides of a triangle]}$ … (2)

Now since BD is a straight line,

$\mathrm{\angle }BAC+\mathrm{\angle }CAD={180}^{\circ }$ … (3)

And we know,

$\mathrm{\angle }BAC=\mathrm{\angle }ADC+\mathrm{\angle }ACD$ $\text{[Exterior angle of a triangle = sum of opposite interior angles]}$

$\Rightarrow \mathrm{\angle }BAC=2\mathrm{\angle }ACD$ $\text{[From 2]}$ … (4)

Similarly,

$\mathrm{\angle }CAD=\mathrm{\angle }ABC+\mathrm{\angle }ACB$

$\Rightarrow \mathrm{\angle }CAD=2\mathrm{\angle }ACB$ $\text{[From 1]}$ … (5)

$\therefore 2\mathrm{\angle }ACB+2\mathrm{\angle }ACD={180}^{\circ }$         $\text{[From 3, 4 and 5]}$

$\Rightarrow \mathrm{\angle }ACB+\mathrm{\angle }ACD={90}^{\circ }$

$\Rightarrow \mathrm{\angle }BCD={90}^{\circ }$

Hence proved.

7. ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

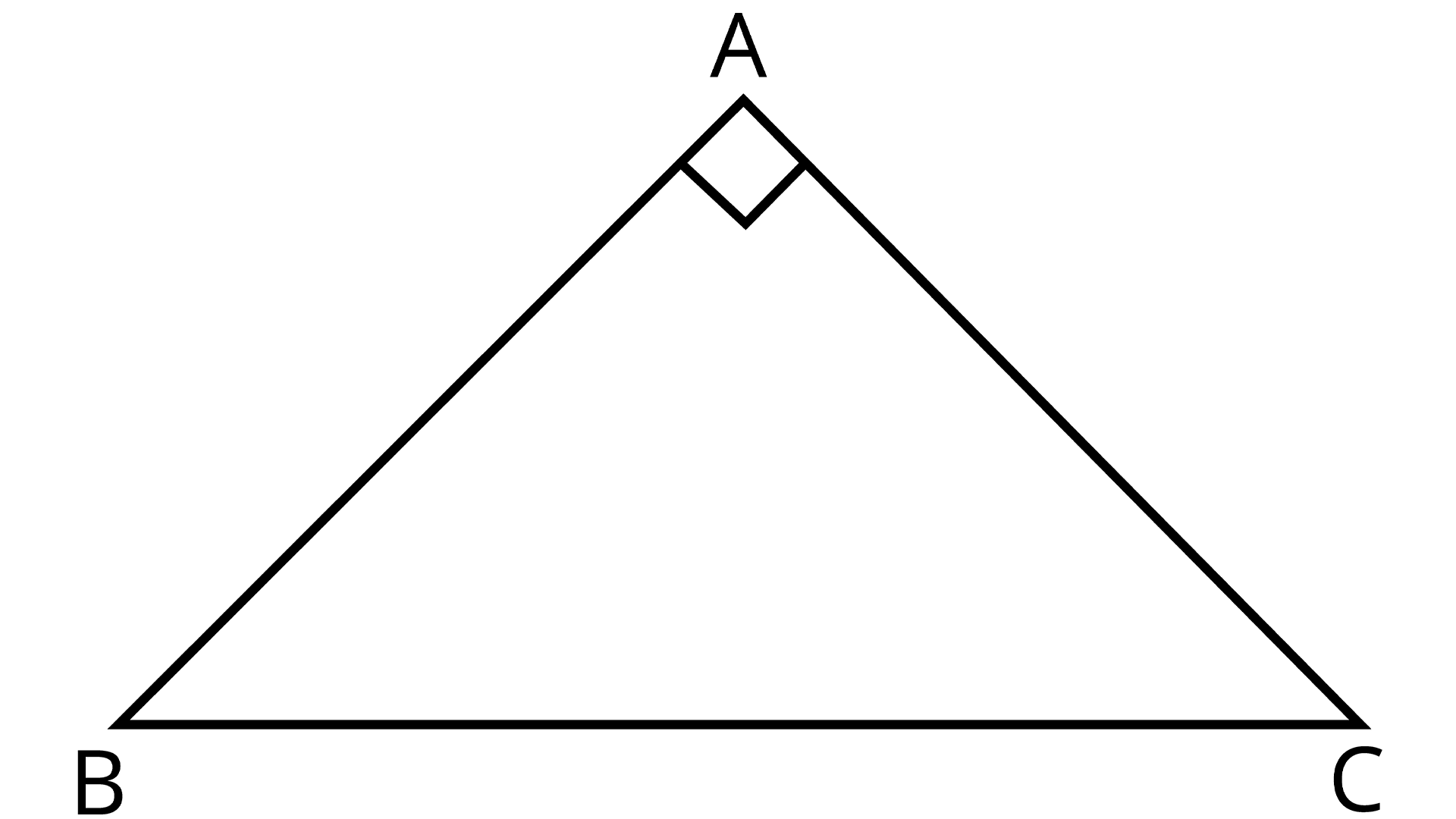
Right - Angled Triangle ABC

Ans: Since AB = AC,

$\mathrm{\angle }B=\mathrm{\angle }C$

$\text{[Angles opposite to equal sides of a triangle]}$

Now, we know

$\mathrm{\angle }A+\mathrm{\angle }B+\mathrm{\angle }C={180}^{\circ }$

$\text{[Angle sum property]}$

$\Rightarrow \mathrm{\angle }A+2\mathrm{\angle }C={180}^{\circ }$

$\Rightarrow {90}^{\circ }+2\mathrm{\angle }C={180}^{\circ }$

$\Rightarrow 2\mathrm{\angle }C={90}^{\circ }$

$\Rightarrow \mathrm{\angle }C={45}^{\circ }$

$\therefore \mathrm{\angle }B={45}^{\circ }$

Hence $\mathrm{\angle }B$ and $\mathrm{\angle }C$ are each 45${}^{\circ }$

8. Show that the angles of an equilateral triangle are 60º each.

Ans:

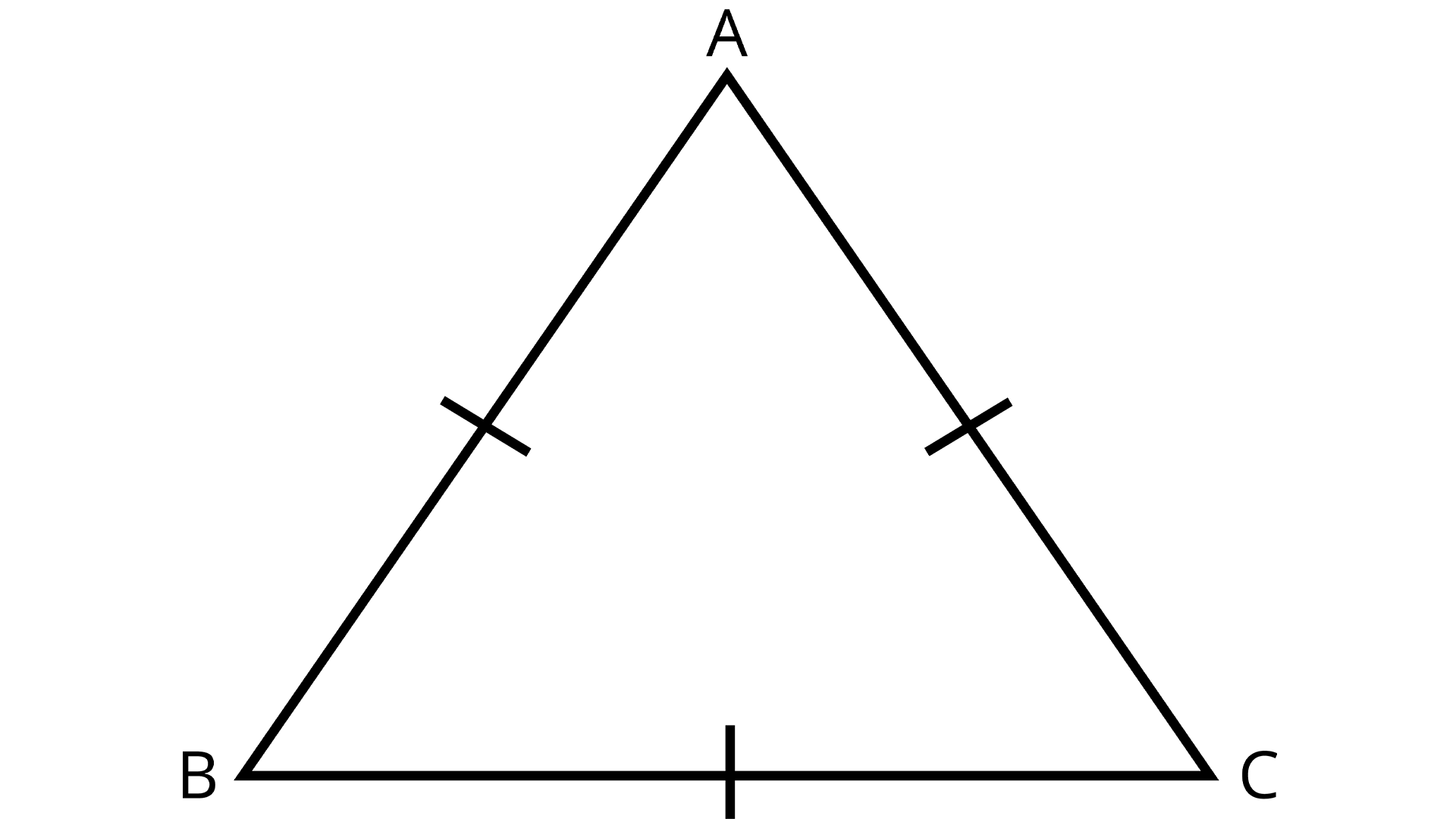
Equilateral Triangle

In $\mathrm{\angle }B=\mathrm{\angle }C$ $\text{[Angles opposite to equal sides of a triangle]}$

Similarly,

$\mathrm{\angle }A=\mathrm{\angle }B$

$\text{[Angles opposite to equal sides of a triangle]}$

$\Rightarrow \mathrm{\angle }A=\mathrm{\angle }B=\mathrm{\angle }C$

Now, we know that

$\mathrm{\angle }A+\mathrm{\angle }B+\mathrm{\angle }C={180}^{\circ }$ $\text{[Angle sum property]}$

$\Rightarrow \mathrm{\angle }A+\mathrm{\angle }A+\mathrm{\angle }A={180}^{\circ }$

$\Rightarrow 3\mathrm{\angle }A={180}^{\circ }$

$\Rightarrow \mathrm{\angle }A={60}^{\circ }$ 

$\therefore \mathrm{\angle }A=\mathrm{\angle }B=\mathrm{\angle }C={60}^{\circ }$

Hence proved.

Exercise 7.3

1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that

(i) $$\mathrm{\Delta }ABD\cong \mathrm{\Delta }ACD$$

(ii) $$\mathrm{\Delta }ABP\cong \mathrm{\Delta }ACP$$

(iii) AP bisects $\mathrm{\angle }A$ as well as $\mathrm{\angle }D$

(iv)AP is the bisector of BC

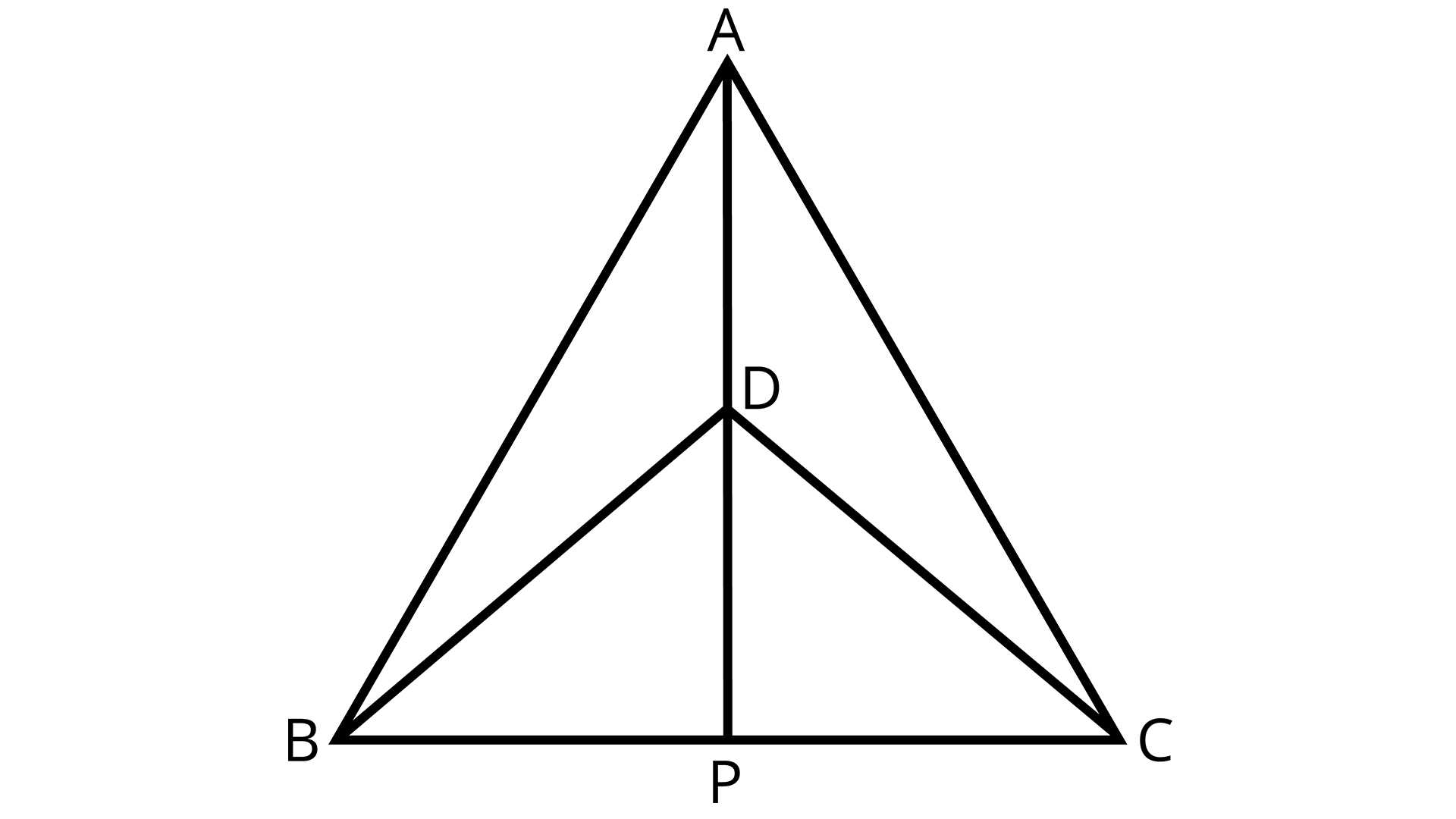
Two Isosceles Triangle on the same Base

Ans: (i) In $\mathrm{\Delta }ABD$ and $\mathrm{\Delta }ACD$,

$AB=AC$

$\text{[Equal sides of isosceles triangle]}$

$DB=DC$

$\text{[Equal sides of isosceles triangle]}$

AD=AD (Common)

$\therefore \mathrm{\Delta }ABD\cong \mathrm{\Delta }ACD$ $\text{[By SSS]}$

$\Rightarrow \mathrm{\angle }BAD=\mathrm{\angle }CAD$ [CPCT]

$\Rightarrow \mathrm{\angle }BAP=\mathrm{\angle }CAP$ … (1)

And $\mathrm{\angle }ADB=\mathrm{\angle }ADC$ (CPCT) … (2)

(ii) In $\mathrm{\Delta }ABP$ and $\mathrm{\Delta }ACP$

$AB=AC$

$\text{[Equal sides of isosceles triangle]}$

$\mathrm{\angle }BAP=\mathrm{\angle }CAP$ $\text{[From 1]}$

$AP=AP$ (Common)

$\therefore \mathrm{\Delta }ABP\cong \mathrm{\Delta }ACP$

$\text{[By SAS]}$

$\therefore BP=CP$ (CPCT) … (3)

Similarly, $\mathrm{\angle }APB=\mathrm{\angle }APC$ (CPCT) … (4)

(iii) AP is bisector of $\mathrm{\angle }A$

$\text{[From 1]}$

Now, since AP is a line segment

$\therefore \mathrm{\angle }ADB+\mathrm{\angle }BDP={180}^{\circ }$ … (5)

Similarly, $\mathrm{\angle }ADC+\mathrm{\angle }CDP={180}^{\circ }$ … (6)

Comparing equations 2, 5 and 6 we can say that

$\mathrm{\angle }BDP=\mathrm{\angle }CDP$

$\therefore$AP bisects $\mathrm{\angle }D$

Hence AP bisects both $\mathrm{\angle }A$ and $\mathrm{\angle }D$

(iv)We know,

$\mathrm{\angle }APB+\mathrm{\angle }APC={180}^{\circ }$

$\Rightarrow \mathrm{\angle }APB+\mathrm{\angle }APB={180}^{\circ }$

$\text{[From 4]}$

$\Rightarrow \mathrm{\angle }APB={90}^{\circ }$ … (7)

From equations 3 and 7 we can say that,

AP is perpendicular bisector of BC.

2. AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that

(i) AD bisects BC

(ii) AD bisects $\mathrm{\angle }A$

Ans:

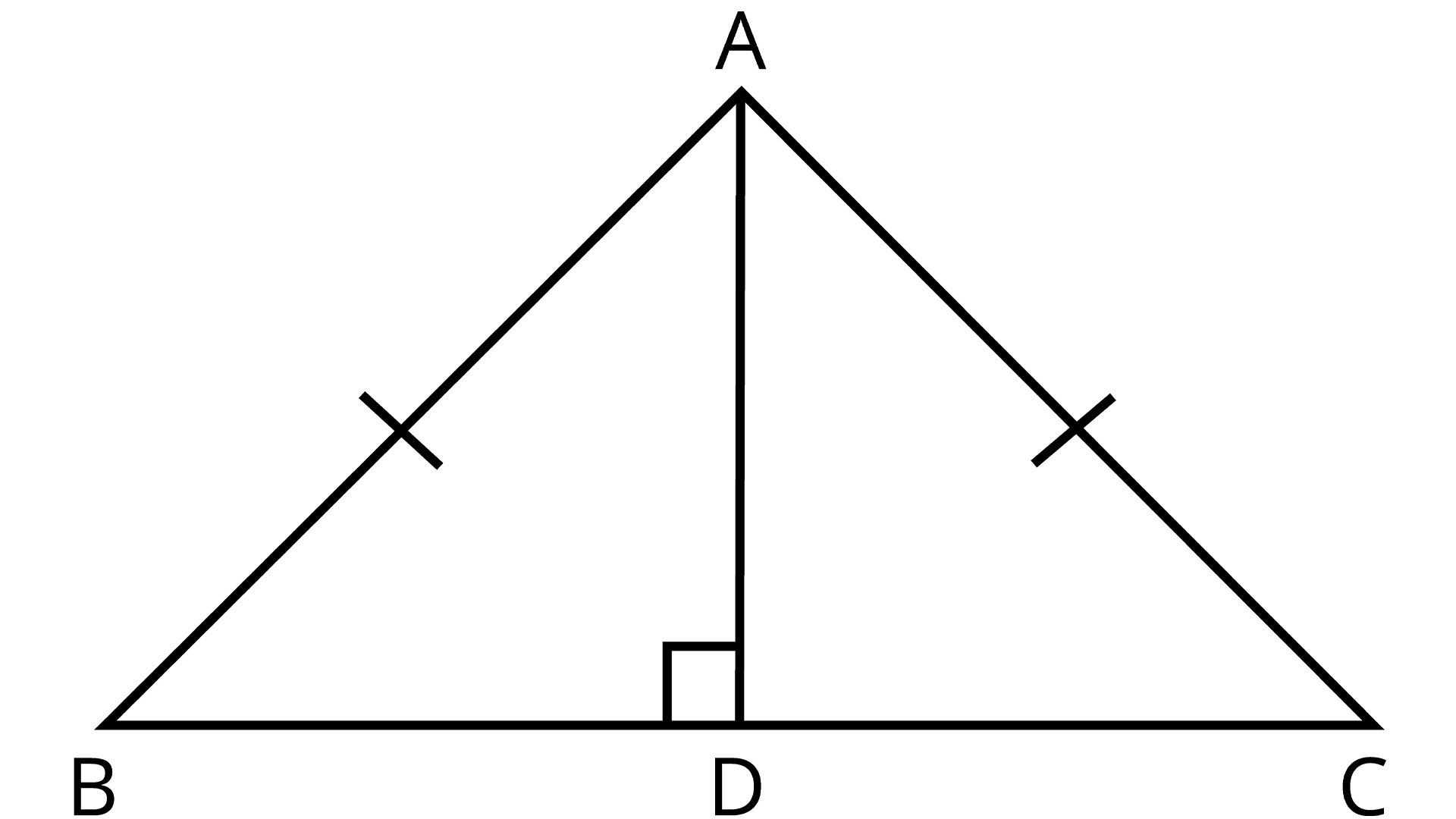
Isosceles Triangle BC with AB = AC

In $\mathrm{\Delta }ADB$ and $\mathrm{\Delta }ADC$

$AB=AC$ (Given)

$AD=AD$ (Common)

$\mathrm{\angle }ADB=\mathrm{\angle }ADC$ $\text{[Each 90°]}$

$\therefore \mathrm{\Delta }ADB\cong \mathrm{\Delta }ADC$ $\text{[By RHS]}$

$\Rightarrow BD=DC$ (CPCT)

Therefore, AD is bisector of BC

Similarly, $\mathrm{\angle }BAD=\mathrm{\angle }CAD$ (CPCT)

Therefore, AD bisects $\mathrm{\angle }A$as well.

3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see the given figure). Show that:

(i)$$\mathrm{\Delta }ABM\cong \mathrm{\Delta }PQN$$

(ii)$$\mathrm{\Delta }ABC\cong \mathrm{\Delta }PQR$$

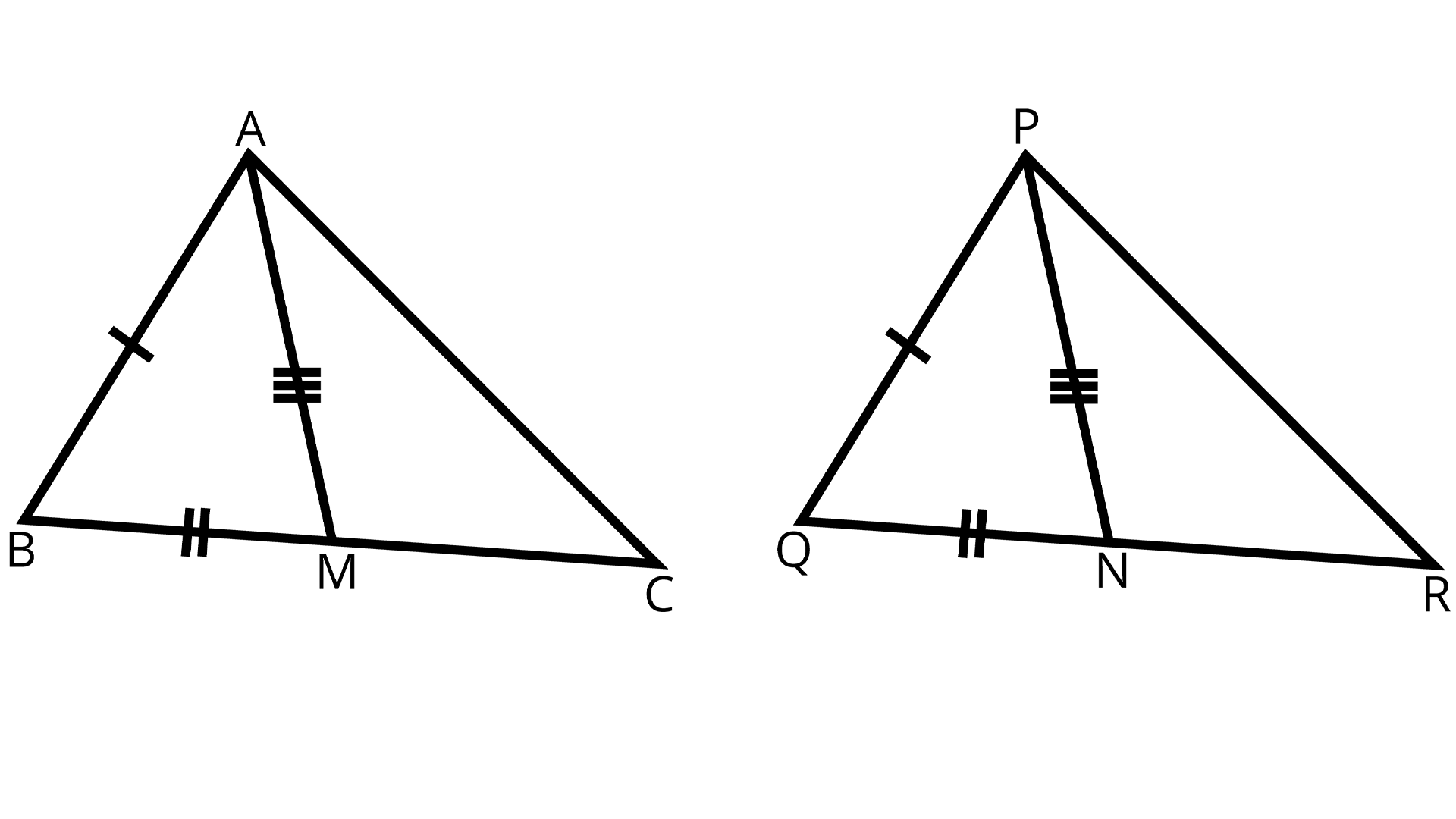
Two Triangles with Their Corresponding Parts

Ans: (i) We know that $BC=QR$ … (1)

Now, Since AM is median of ΔABC,

$\Rightarrow BM={\displaystyle \frac{1}{2}}BC$ … (2)

Similarly, PN is median of ΔPQR,

$\Rightarrow QN={\displaystyle \frac{1}{2}}QR$ … (3)

From equations 1, 2 and 3, we can say that,

$BM=QN$ … (4)

Now in $\mathrm{\Delta }ABM$ and $\mathrm{\Delta }PQN$

$$AB=PQ$$ (Given)

$$BM=QN$$ $\text{[From 4]}$

AM=PN (Given)

$\therefore \mathrm{\Delta }ABM\cong \mathrm{\Delta }PQN$ $\text{[By SSS]}$

$\Rightarrow \mathrm{\angle }ABM=\mathrm{\angle }AQN$ (CPCT)

$\Rightarrow \mathrm{\angle }ABC=\mathrm{\angle }PQR$ … (5)

(ii) Now in $\mathrm{\Delta }ABC$ and $\mathrm{\Delta }PQR$,

$AB=PQ$ (Given)

$\mathrm{\angle }ABC=\mathrm{\angle }PQR$ $\text{[From 5]}$

$BC=QR$ (Given)

$$\mathrm{\Delta }ABC\cong \mathrm{\Delta }PQR$$         $\text{[By SAS]}$

4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Ans:

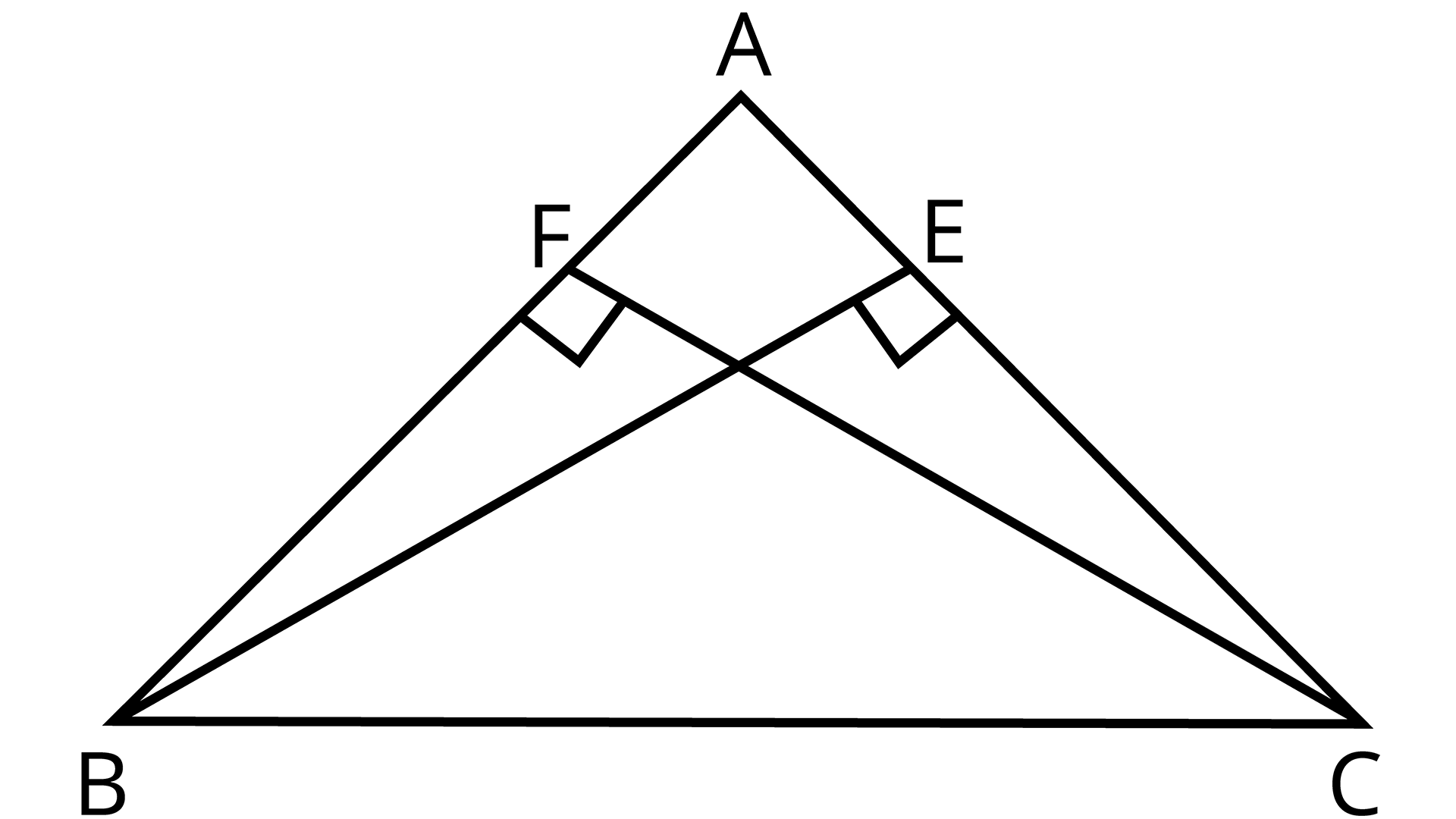
Two Equal Altitudes BE and CF of Triangle ABC

In $\mathrm{\Delta }BEC$ and $\mathrm{\Delta }CFB$

$BE=CF$ (Given)

$\mathrm{\angle }BEC=\mathrm{\angle }CFB$

$\text{[Each 90°]}$

BC=CB (Common)

$\therefore \mathrm{\Delta }BEC\cong \mathrm{\Delta }CFB$ $\text{[By RHS Congruency]}$

$\Rightarrow \mathrm{\angle }BCE=\mathrm{\angle }CBF$               (CPCT)

$\therefore AB=AC$ $\text{[Sides opposite to equal angles of a triangle are equal]}$

Therefore, ΔABC is an isosceles triangle.

5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B= ∠C.

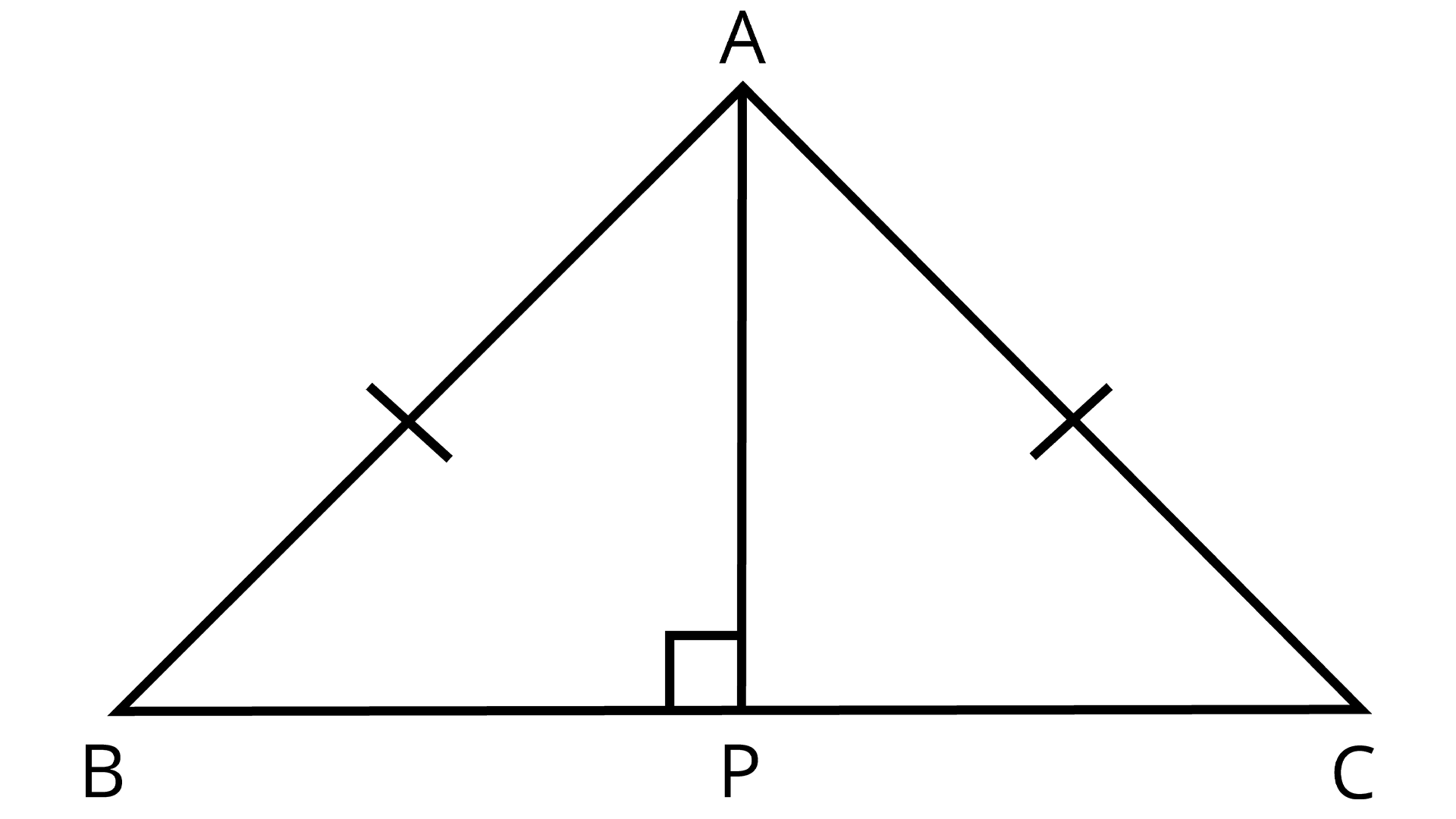
Isosceles Triangle ABC with AB = AC

Ans: In $\mathrm{\Delta }ABP$ and $\mathrm{\Delta }ACP$

$AB=AC$ (Given)

$AP=AP$ (Common)

$\mathrm{\angle }APB=\mathrm{\angle }APC$ $\text{[Each 90°]}$

$\therefore \mathrm{\Delta }ABP\cong \mathrm{\Delta }ACP$

$\text{[By RHS]}$

$\Rightarrow \mathrm{\angle }ABP=\mathrm{\angle }ACP$         (CPCT)

Overview of Deleted Syllabus for CBSE Class 9 Maths Chapter 7 Triangles

Class 9 Maths Chapter 7: Exercises Breakdown

Conclusion

Triangle-related NCERT Solutions for Class 9 Chapter 7 from Vedantu are an excellent resource for understanding important geometric ideas. Because it provides the foundation for understanding more difficult geometrical structures that students will encounter in higher grades, this chapter is essential. Along with several congruence criteria including SAS, SSS, and ASA, it concentrates on key theorems such as the Pythagorean Theorem, Angle Sum Property, and Triangle Inequality. The importance of understanding both the theoretical and practical elements of these geometric principles is made clear by the three to five problems from this chapter that have frequently appeared in earlier year's question papers.

Other Study Material for CBSE Class 9 Maths Chapter 7

Chapter-Specific NCERT Solutions for Class 9 Maths

Given below are the chapter-wise NCERT Solutions for Class 9 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Study Materials for CBSE Class 9 Maths