NCERT Solutions for Class 9 Maths Chapter 9 - In Hindi

प्रश्नावली -9.1

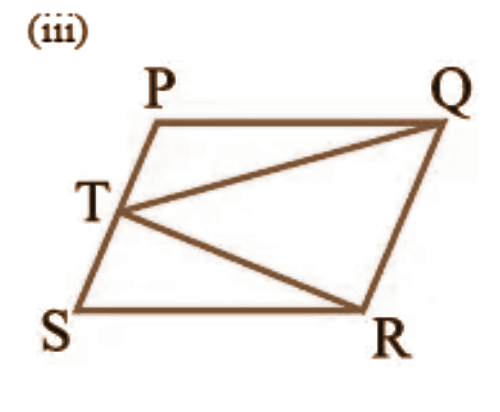
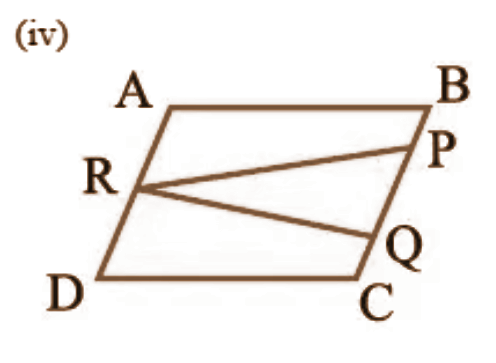
1. निम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हैं? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समांतर रेखाएँ लिखिए।

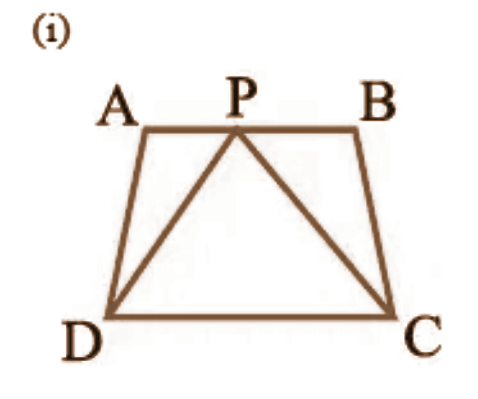
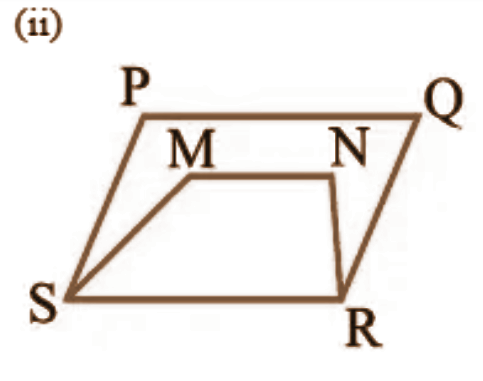
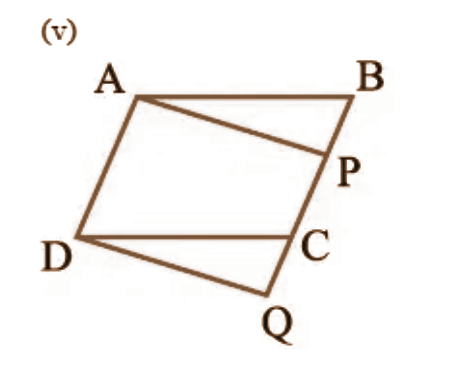
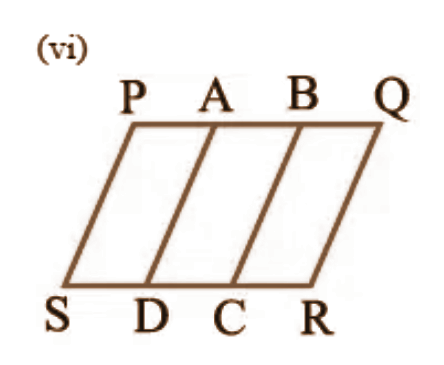
उत्तर: \[\left( i \right)\text{ }ABCD\] और \[PDC\],

\[~\left( iii \right)\text{ }PQRS\] और \[TQR\] 

\[\left( iv \right)\text{ }ABCD\] और \[PQR\]. 

\[\left( v \right)\text{ }ABCD\] और \[APCD\], 

\[\left( vi \right)\text{ }PQRS,\text{ }PADS,\text{ }ABCD\] और \[BQRC\]

प्रश्नावली 9.2

1. इस आकृति में \[\mathbf{ABCD}\] एक समांतर चतुर्भुज है, \[\mathbf{AE}\bot \mathbf{DC}\] और \[\mathbf{CF}\bot \mathbf{AD}\] है। यदि \[\mathbf{AB}\text{ }=\mathbf{16}\text{ }\mathbf{cm},\text{ }\mathbf{AE}\text{ }=\text{ }\mathbf{8}\text{ }\mathbf{cm}\] और \[\mathbf{CF}\text{ }=\text{ }\mathbf{10}\text{ }\mathbf{cm}\] है, तो \[\mathbf{AD}\] ज्ञात कीजिए।

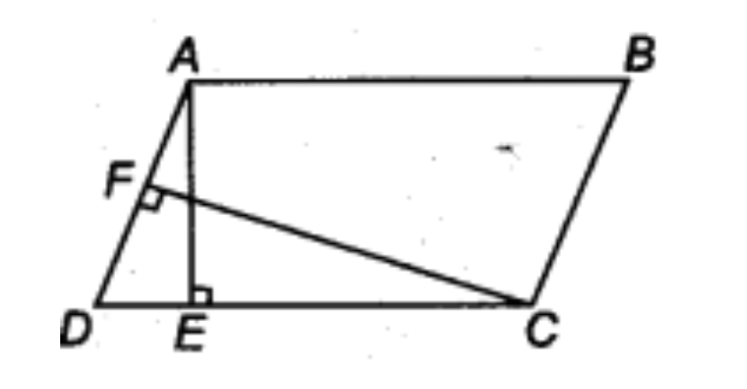
उत्तर: दिया गया है; \[AB\text{ }=\text{ }16\text{ }cm,\text{ }AE\text{ }=\text{ }8\text{ }cm\] और \[CF\text{ }=\text{ }10\text{ }cm\]

\[AB\text{ }=\text{ }DC\text{ }=\text{ }16\text{ }cm\] (क्योंकि \[AD||BC\])

क्षेत्रफल  \[\left( ABCD \right)\]= ऊंचाई \[\times \]लंबाई 

\[=AE\times DC=8\times 16=128c{{m}^{2}}\]

क्षेत्रफल  \[\left( ABCD \right)\]= ऊंचाई \[\times \]लंबाई 

या, \[10\times AD=128c{{m}^{2}}\]

या, \[AD\text{ }=~\dfrac{128}{10}=12.8cm\]

2. यदि \[\mathbf{E},\text{ }\mathbf{F},\text{ }\mathbf{G}\] और \[\mathbf{H}\] क्रमश: समांतर चतुर्भुज \[\mathbf{ABCD}\] की भुजाओं के मध्य बिंदु हैं, तो दर्शाइए कि \[\mathbf{ar}\left( \mathbf{EFGH} \right)\text{ }=~\dfrac{\mathbf{1}}{\mathbf{2}}~\mathbf{ar}\text{ }\left( \mathbf{ABCD} \right)\]है।

उत्तर: इस आकृति में एक समांतर चतुर्भुज \[ABCD\] है जिसमें \[E,\text{ }F,\text{ }G\] और \[H\] इसकी भुजाओं के मध्य बिंदु हैं। समांतर चतुर्भुज की ऊँचाई \[AM\] है। \[\Delta EFH\] की ऊँचाई \[EO\] है, और \[\Delta FGH\] की ऊँचाई \[GN\] है।

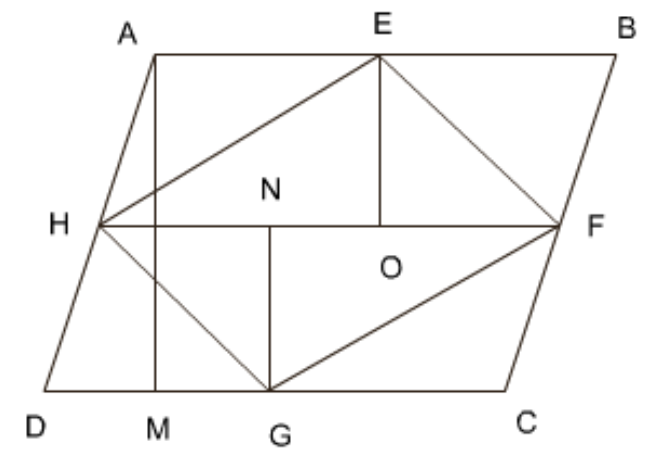
\[EO\text{ }=\text{ }GN\text{ }=\dfrac{~1}{2}~AM\] (क्योंकि \[AD\] और \[BC\] के मध्य बिंदुओं को छूती है।)

क्षेत्रफल  \[\left( ABCD \right)\]= ऊंचाई \[\times \]लंबाई \[=\text{ }AM~\times DC\ldots \ldots \ldots \ldots \ldots \ldots \left( 1 \right)\]

\[Area\text{ }\left( EFGH \right)\text{ }=\text{ }ar\left( \Delta EFH \right)\text{ }+\text{ }ar\left( \Delta FGH \right)\]

\[\begin{align} & \begin{array}{*{35}{l}} =\dfrac{1}{2}\times EO\times HF+\dfrac{1}{2}\times GN\times HF  \\ =\dfrac{1}{2}\left( EO\times HF+GN\times HF \right)  \\ \end{array} \\  & =\dfrac{1}{2}\left( EO\times HF+EO\times HF \right)~ \\  \end{align}\] [क्योंकि \[EO\text{ }=\text{ }GN\])

\[=\dfrac{1}{2}\times 2\times \left( EO\times HF \right)=EO\times HF~\ldots \ldots \ldots \ldots \ldots \ldots \left( 2 \right)\]

चूँकि \[EO=\dfrac{1}{2}AM\]

और \[HF\text{ }=\text{ }DC\]

समीकरण \[(1)\]और \[(2)\]से यह साफ है कि \[ar\left( EFGH \right)\text{ }=~\dfrac{1}{2}ar\left( ABCD \right)\]सिद्ध हुआ

3. \[\mathbf{P}\] और \[\mathbf{Q}\] क्रमश: समांतर चतुर्भुज \[\mathbf{ABCD}\] की भुजाओं \[\mathbf{DC}\] और \[\mathbf{AD}\] पर स्थित मध्य बिंदु हैं। दर्शाइए कि \[\mathbf{ar}\left( \mathbf{APB} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{BQC} \right)\]है।

उत्तर: मान लीजिए कि आधार \[AB\] के लिए ऊँचाई \[{{h}_{1}}\] है और आधार BC के लिए ऊँचाई \[{{h}_{2}}\] है।

क्षेत्रफल  \[\left( ABCD \right)~={{h}_{1}}\times AB={{h}_{2}}\times BC\]

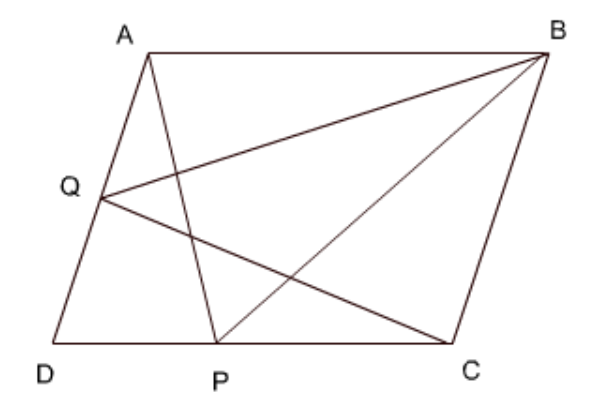
क्षेत्रफल \[\left( \Delta APB \right)~=\dfrac{1}{2}\times {{h}_{1}}\times AB\]

क्षेत्रफल \[\left( \Delta BQC \right)~=\dfrac{1}{2}\times {{h}_{2}}\times BC\]

ऊपर के समीकरणों से यह सिद्ध होता है कि \[ar\left( \Delta APB \right)\text{ }=\text{ }ar\left( \Delta BQC \right)\]

4. इस आकृति में \[\mathbf{P}\] समांतर चतुर्भुज \[\mathbf{ABCD}\] के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि

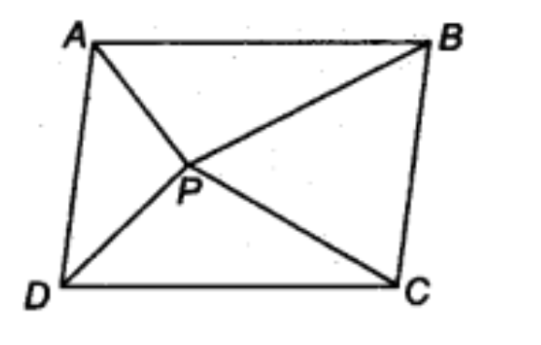
1. \[\mathbf{ar}\left( \mathbf{APB} \right)\text{ }+\text{ }\mathbf{ar}\left( \mathbf{PCD} \right)\text{ }=~\dfrac{1}{2}\mathbf{ar}\left( \mathbf{ABCD} \right)\]

2. \[\mathbf{ar}\left( \mathbf{APD} \right)\text{ }+\text{ }\mathbf{ar}\left( \mathbf{PBC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{APB} \right)\text{ }+\text{ }\mathbf{ar}\left( \mathbf{PCD} \right)\] 

(संकेत: \[P\] से होकर \[AB\] के समांतर एक रेखा खींचिए।)

उत्तर: बिंदु \[P\] से गुजरने वाली रेखा \[MN||AB\] खींचिए। अब मान लीजिए कि समांतर चतुर्भुज \[ABNM\] की ऊँचाई \[{{h}_{1}}\] है, \[MNCD\] की ऊँचाई \[{{h}_{2}}\] है तथा \[ABCD\] की ऊँचाई \[h\] है।.

सभी समांतर चतुर्भुजों आ आधार होगा \[AB\]

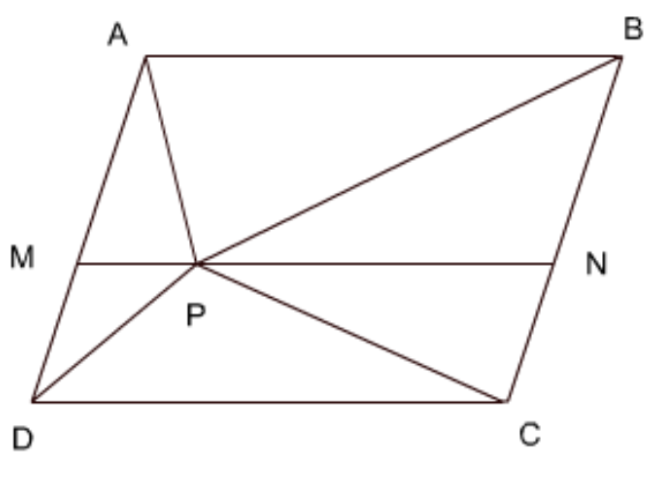
\[\begin{array}{*{35}{l}} ar\left( ABCD \right)\text{ }=\text{ }ar\left( ABNM \right)\text{ }+\text{ }ar\left( MNCD \right)  \\ ar\left( \Delta APB \right)\text{ }=~\dfrac{1}{2}~ar\left( ABNM \right)  \\ ar\left( \Delta PCD \right)\text{ }=~\dfrac{1}{2}~ar\left( MNCD \right)  \\ \end{array}\]

क्योंकि एक ही आधार पर बने त्रिभुज का क्षेत्रफल उस आधार पर बने समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।

इसलिए, \[ar\left( \Delta APB \right)\text{ }+\text{ }ar\left( \Delta PCD \right)\text{ }=~\dfrac{1}{2}~ar\left( ABCD \right)\]

इसी तरह\[,\text{ }ar\left( \Delta APD \right)\text{ }+\text{ }ar\left( \Delta PBC \right)\text{ }=~\dfrac{1}{2}ar\left( ABCD \right)\]को भी सिद्ध किया जा सकता है।

इससे पता चलता है कि \[ar\left( APD \right)\text{ }+\text{ }ar\left( PBC \right)\text{ }=\text{ }ar\left( APB \right)\text{ }+\text{ }ar\left( PCD \right)\]

5. इस आकृति में PQRS और ABRS समांतर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि

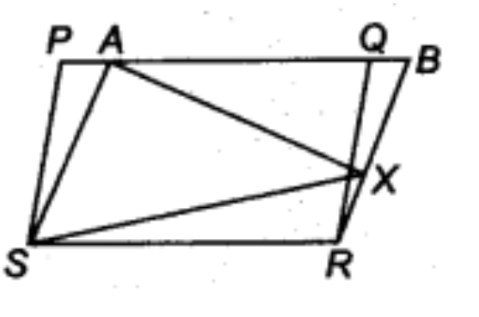
1. \[ar\left( PQRS \right)\text{ }=\text{ }ar\left( ABRS \right)\]

2. \[ar\left( AXS \right)\text{ }=~\dfrac{1}{2}~ar\left( PQRS \right)\]

उत्तर: हम जानते हैं कि एक ही आधार और एक ही ऊँचाई वाले समांतर चतुर्भुजों के क्षेत्रफल बराबर होते हैं।

इसलिए\[,\text{ }ar\left( PQRS \right)\text{ }=\text{ }ar\left( ABRS \right)\]

हम यह भी जानते हैं कि उसी आधार और ऊँचाई पर बने त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।

इसलिए, \[ar\left( AXS \right)\text{ }=~\dfrac{1}{2}~ar\left( PQRS \right)\]

6. एक किसान के पास समांतर चतुर्भुज \[\mathbf{PQRS}\] के रूप में एक खेत था। उसने \[\mathbf{RS}\] पर स्थित कोई बिंदु \[\mathbf{A}\] लिया और उसे \[\mathbf{P}\] और \[\mathbf{Q}\] से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर बराबर भागों में अलग-अलग बोना चाहती है। वह ऐसा कैसे करे?

उत्तर: इस आकृति में उस खेत के विभाजन को दिखाया गया है। खेत को तीन भागों में बाँटा गया है। हर भाग त्रिभुज के आकार का है।

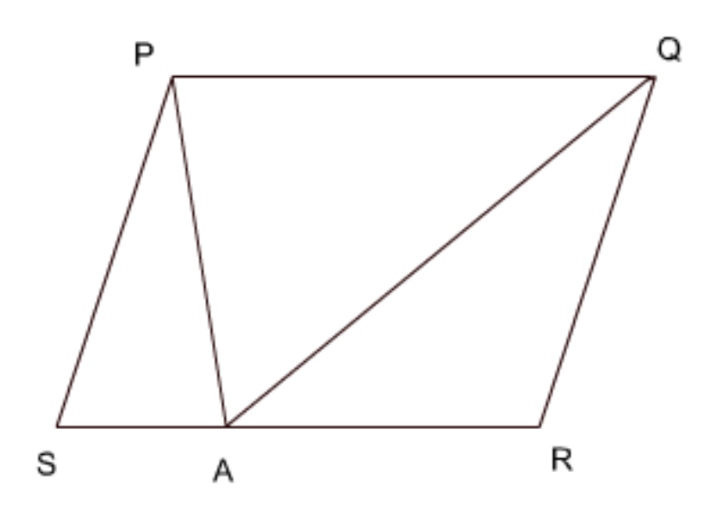
\[Area\left( \Delta PQA \right)\text{ }=~\dfrac{1}{2}~ar\left( PQRS \right)\]

इसका मतलब है कि बाकी के दो त्रिभुजों के क्षेत्रफल का योग \[=ar\left( \Delta PQA \right)\]

किसान त्रिभुज \[PQA\] में गेहूँ की खेती कर सकता है और बाकी के त्रिभुजों में दाल की

प्रश्नावली 9.3

1. इस आकृति में \[\mathbf{\Delta ABC}\] की एक माध्यिका \[\mathbf{AD}\] पर स्थित कोई बिंदु E है। दर्शाइए कि \[\mathbf{\Delta }\left( \mathbf{ABE} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ACE} \right)\]है।

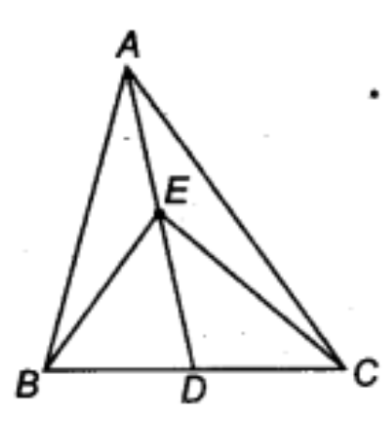
उत्तर: माध्यिका किसी भी त्रिभुज को दो समान त्रिभुजों में बाँटती है।

इसलिए, \[ar\left( ABD \right)\text{ }=\text{ }ar\left( ACD \right)\]

इसी तरह, \[ar\left( BED \right)\text{ }=\text{ }ar\left( DEC \right)\]

यदि हम \[\Delta BEC\] को हटाते हैं, यानि ΔBED + ΔDEC को हटाते हैं तो

\[ar\left( ABE \right)\text{ }=\text{ }ar\left( ACE \right)\]सिद्ध हुआ

2.: ΔABC में E माध्यिका AD का मध्य बिंदु है। दर्शाइए कि ar(BED) = 1414है।

उत्तर: \[\Delta BEC\] की माध्यिका \[ED\] है।

इसलिए, \[ar\left( BED \right)\text{ }=\text{ }ar\left( CED \right)\]

साथ में, \[ar\left( BEC \right)\text{ }=~1212~ar\left( ABC \right)\]

इन समीकरणों से यह साफ है कि \[ar\left( BED \right)\text{ }=~1414~ar\left( ABC \right)\]

3. दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।

उत्तर: \[ABCD\] एक समांतर चतुर्भुज है जिसके विकर्ण \[AC\] और \[BD\] परस्पर बिंदु \[O\] काटते हैं।

सिद्ध करना है: \[ar\left( AOB \right)\text{ }=\text{ }ar\left( AOC \right)\text{ }=\text{ }ar\left( BOC \right)\text{ }=\text{ }ar\left( AOD \right)\]

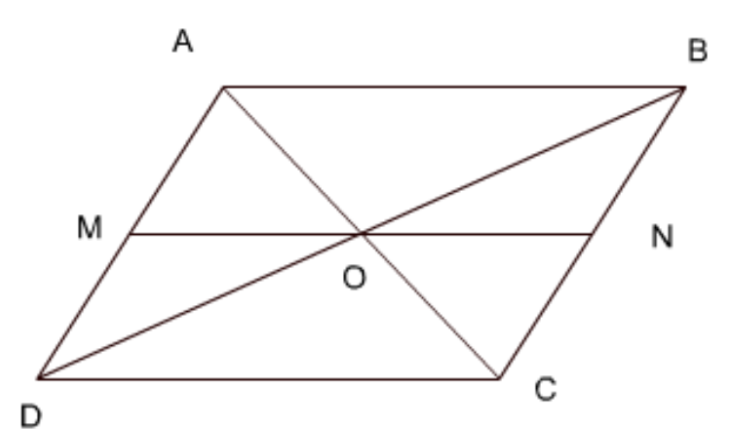
हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे के समद्विभाजक होते हैं। इसलिए \[AD\] और \[BC\] के मध्य बिंदु \[M\] और \[N\] हैं।

इसका मतलब है: \[ar\left( ABNM \right)\text{ }=\text{ }ar\left( MNCD \right)\text{ }=~\dfrac{1}{2}~ar\left( ABCD \right)\]

\[ar\left( ABO \right)\text{ }=\dfrac{1}{2}~ar\left( ABNM \right)\] 

(क्योंकि समान आधार पर बने त्रिभुज का क्षेत्रफल उस आधार पर बने समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।

इसी तरह, \[ar\left( DOC \right)\text{ }=~\dfrac{1}{2}ar\left( MNCD \right)\]

यानि; \[ar\left( ABO \right)\text{ }=\text{ }ar\left( DOC \right)\text{ }=~\dfrac{1}{4}~ar\left( ABCD \right)\]

इसी प्रकार निम्नलिखित को सिद्ध किया जा सकता है:

\[ar\left( AOD \right)\text{ }=\text{ }ar\left( BON \right)\text{ }=~\dfrac{1}{4}~ar\left( ABCD \right)\]

इसलिए\[,\text{ }ar\left( AOB \right)\text{ }=\text{ }ar\left( BOC \right)\text{ }=\text{ }ar\left( DOC \right)\text{ }=\text{ }ar\left( AOD \right)\text{ }=~\dfrac{1}{4}~ar\left( ABCD \right)\]

4. इस आकृति में \[\mathbf{ABC}\] और \[\mathbf{ABD}\] एक ही आधार \[\mathbf{AB}\] पर बने दो त्रिभुज हैं। यदि रेखाखंड \[\mathbf{CD}\] रेखाखंड \[\mathbf{AB}\] से \[\mathbf{O}\] बिंदु पर समद्विभाजित होता है, तो दर्शाइए कि \[\mathbf{ar}\left( \mathbf{ABC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ABD} \right)\] है।

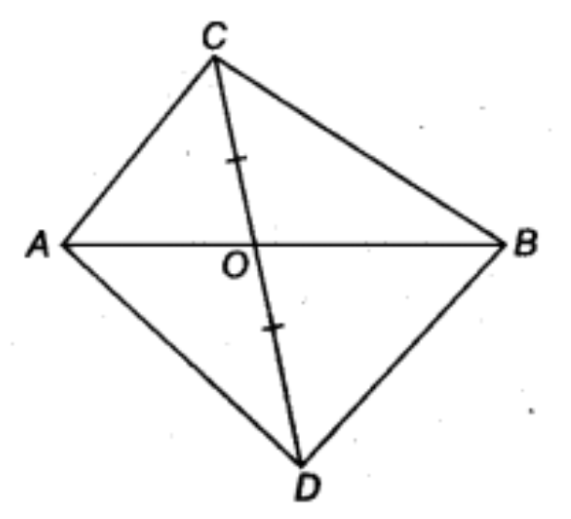
उत्तर: चूँकि \[CD\] को \[AO\] और \[BO\] समद्विभाजित करते हैं इसलिए ये क्रमश: \[ACD\] और \[BCD\] की माध्यिका हैं।

इसलिए, \[ar\left( AOC \right)\text{ }=\text{ }ar\left( AOD \right)\]

इसी प्रकार, \[ar\left( COB \right)\text{ }=\text{ }ar\left( DOB \right)\]

इसलिए, \[ar\left( AOC \right)\text{ }+\text{ }ar\left( COB \right)\text{ }=\text{ }ar\left( AOD \right)\text{ }+\text{ }ar\left( DOB \right)\]

या, \[ar\left( ABC \right)\text{ }=\text{ }ar\left( ABD \right)\]सिद्ध हुआ

5. \[\mathbf{D},\text{ }\mathbf{E}\] और \[\mathbf{F}\] क्रमश: त्रिभुज की भुजाओं और के मध्य बिंदु हैं। दर्शाइए कि

1. \[\mathbf{BDEF}\] एक समांतर चतुर्भुज है

2. \[\mathbf{ar}\left( \mathbf{DEF} \right)\text{ }=\dfrac{1}{4}\mathbf{ar}\left( \mathbf{ABC} \right)\]

3. \[\mathbf{ar}\left( \mathbf{BDEf} \right)\text{ }=~\dfrac{1}{2}~\mathbf{ar}\left( \mathbf{ABC} \right)\]

उत्तर:

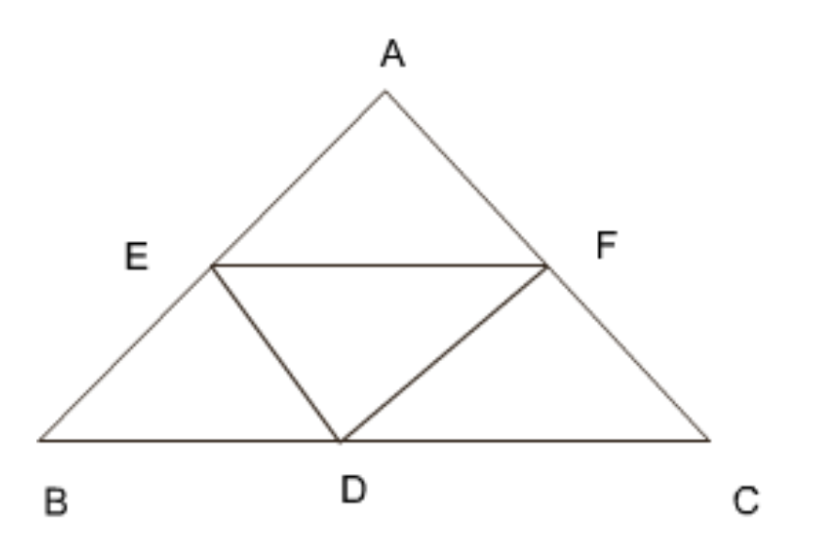
मध्य बिंदु प्रमेय के अनुसार: \[BD||EF\]

\[BD\text{ }=~\dfrac{1}{2}~BC\] (क्योंकि \[D\] मध्य बिंदु है।)

इसलिए, \[EF\text{ }=\text{ }BD\]

चूँकि \[EF\text{ }=\text{ }BD\]

इसलिए, \[BDFE\] एक समांतर चतुर्भुज है।

इसी तरह यह सिद्ध किया जा सकता है कि \[EFDC\] और \[AEDF\] समांतर चतुर्भुज हैं।

चूँकि \[BD\text{ }=\text{ }CD\text{ }=\text{ }EF\]

इसलिए, \[ar\left( BDFE \right)\text{ }=\text{ }ar\left( EFDC \right)\]

त्रिभुज \[BED\] और \[EFD\] में:

\[\begin{array}{*{35}{l}} BD\text{ }=\text{ }EF  \\ DE\text{ }=\text{ }DE  \\ \end{array}\]

इसलिए \[SSS\] प्रमेय के अनुसार:

\[\Delta BDE\cong \Delta EFD\]

इसी प्रकार यह सिद्ध किया जा सकता है कि \[\Delta EFD\cong \Delta CDF\]

इसी प्रकार यह भी सिद्ध किया जा सकता है कि \[\Delta EFD\cong \Delta FEA\]

इसलिए, \[\Delta BDE\] \[\cong \Delta EFD\cong \Delta CDF\cong \Delta FEA\]

इसलिए, \[ar\left( DEF \right)\text{ }=~\dfrac{1}{4}~ar\left( ABC \right)\]

चूँकि समांतर चतुर्भुज BDFE दो त्रिभुजों से मिलकर बना है।

इसलिए, \[ar\left( BDFE \right)\text{ }=\dfrac{1}{2}~ar\left( ABC \right)\]सिद्ध हुआ।

6. इस आकृति में चतुर्भुज \[\mathbf{ABCD}\] के विकर्ण \[\mathbf{AC}\] और \[\mathbf{BD}\] परस्पर बिंदु \[\mathbf{O}\] पर इस प्रकार प्रतिच्छेद करते हैं कि \[\mathbf{OB}\text{ }=\text{ }\mathbf{OD}\] है। यदि है \[\mathbf{AB}\text{ }=\text{ }\mathbf{CD}\], तो दर्शाइए कि

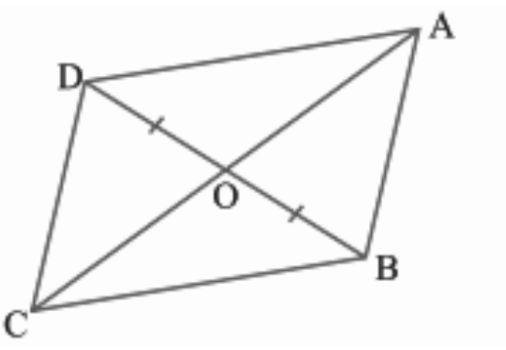
\[\left( \mathbf{a} \right)\text{ }\mathbf{ar}\left( \mathbf{DOC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{AOB} \right)\]

उत्तर: 

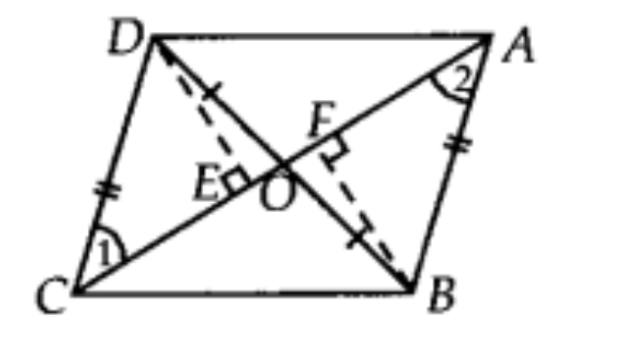
माना \[DE\bot AC\] और \[BF\bot AC\]

त्रिभुज \[DOC\] और \[AOB\] में

\[DC\text{ }=\text{ }AB\] (दिया गया है)

\[DO\text{ }=\text{ }BO\] (दिया गया है)

\[\angle DOC\text{ }=\angle AOB\] (सम्मुख कोण)

इसलिए, \[SAS\] प्रमेय के अनुसार \[\Delta DOC\cong \Delta AOB\]

इसलिए, \[ar\left( DOC \right)\text{ }=\text{ }ar\left( AOB \right)\]

\[\left( \mathbf{b} \right)\text{ }\mathbf{ar}\left( \mathbf{DCB} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ACE} \right)\]

उत्तर: त्रिभुज \[DCB\] और \[ACB\] में

\[DC\text{ }=\text{ }AB\] (दिया गया है)

\[CB\text{ }=\text{ }CB\] (साझा भुजा)

इसलिए, \[SSS\] प्रमेय के अनुसार \[\Delta DCB\cong \Delta ACB\]

इसलिए, \[ar\left( DCB \right)\text{ }=\text{ }ar\left( ACB \right)\]सिद्ध हुआ

\[\left( \mathbf{c} \right)\text{ }\mathbf{DA}\text{ }||\text{ }\mathbf{CB}\] या \[\mathbf{ABCD}\] एक समांतर चतुर्भुज है।

(संकेत: \[\mathbf{D}\] और \[\mathbf{B}\] से \[\mathbf{A}C\] पर लम्ब खींचिए।)

उत्तर: यहाँ पर सम्मुख भुजाएँ बराबर हैं इसलिए यह सिद्ध होता है कि \[ABCD\] एक समांतर चतुर्भुज है और \[DA||CB\] 

7. बिंदु \[\mathbf{D}\] और \[\mathbf{E}\] क्रमश: \[\mathbf{\Delta ABC}\] की भुजाओं \[\mathbf{AB}\] और \[\mathbf{AC}\] पर इस प्रकार स्थित हैं कि \[\mathbf{ar}\left( \mathbf{DBC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{EBC} \right)\]है। दर्शाइए कि \[\mathbf{DE}\text{ }||\text{ }\mathbf{BC}\] है।

उत्तर:

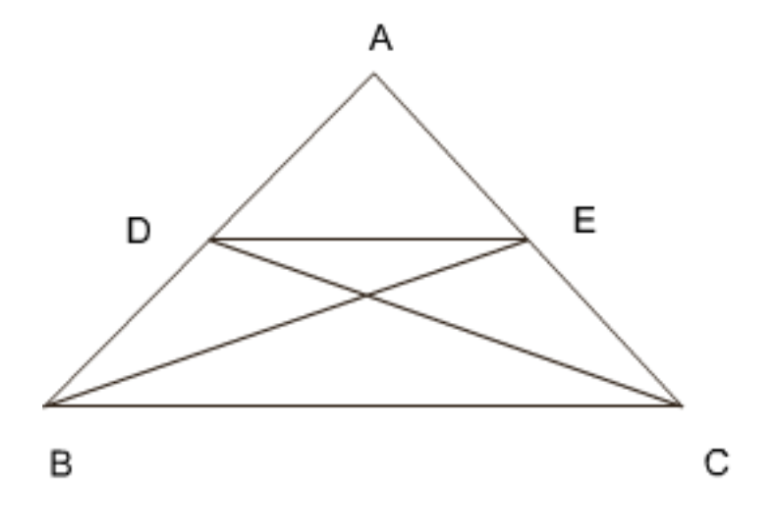
चूँकि \[ar\left( DBC \right)\text{ }=\text{ }ar\left( EBC \right)\]

इन त्रिभुजों का एक ही आधार है \[BC\]

इसलिए दोनों की ऊँचाई भी एक ही होगी। इसलिए दोनों समांतर रेखाओं के एक ही जोड़े के बीच होंगे।

इसलिए\[,\text{ }DE||BC\] सिद्ध हुआ!

8. \[\mathbf{XY}\] त्रिभुज \[\mathbf{ABC}\] की भुजा \[\mathbf{BC}\] के समांतर एक रेखा है। यदि \[\mathbf{BE}\text{ }||\text{ }\mathbf{AC}\] और \[\mathbf{CF}\text{ }||\mathbf{AB}\] रेखा \[\mathbf{XY}\] से क्रमश: \[\mathbf{E}\] और \[\mathbf{F}\] पर मिलती हैं, तो दर्शाइए कि \[\mathbf{ar}\left( \mathbf{ABE} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ACF} \right)\]

उत्तर: \[BEYC\] एक समांतर चतुर्भुज है क्योंकि \[EB||YC\] (दिया गया है \[EB||AC)\]और \[EY||BC\] (क्योंकि \[XY\text{ }||BC\])

त्रिभुज \[AEB\] में और समांतर चतुर्भुज \[BEYC\] में

\[ar\left( AEB \right)\text{ }=~1212~ar\left( BEYC \right)\] (क्योंकि दोनों समांतर रेखाओं के एक ही जोड़े के बीच हैं)

इसी तरह\[,\text{ }ar\left( ACF \right)\text{ }=~1212~ar\left( BXFC \right)\] (क्योंकि दोनों समांतर रेखाओं के एक ही जोड़े के बीच हैं).

अब, \[ar\left( BEYC \right)\text{ }=\text{ }ar\left( BXFC \right)\] (क्योंकि दोनों समांतर रेखाओं के एक ही जोड़े के बीच हैं)

इसलिए, \[ar\left( AEB \right)\text{ }=\text{ }ar\left( ACF \right)\]सिद्ध हुआ!

9. समांतर चतुर्भुज \[\mathbf{ABCD}\] की एक भुजा \[\mathbf{AB}\] को एक बिंदु \[\mathbf{P}\] तक बढ़ाया गया है। \[\mathbf{A}\] से होकर \[\mathbf{CP}\] के समांतर खींची गई रेखा बढ़ाई गई \[\mathbf{CB}\] को \[\mathbf{Q}\] पर मिलती है और फिर समांतर चतुर्भुज को \[\mathbf{PBQR}\] पूरा किया गया है। दर्शाइए कि \[\mathbf{ar}\left( \mathbf{ABCD} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{PBQR} \right)\]है।

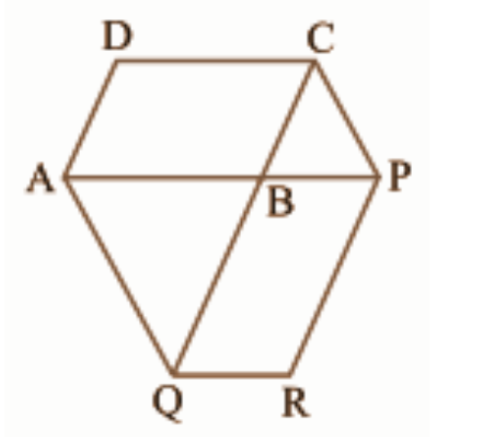
(संकेत: \[AC\] और \[PQ\] को मिलाइए। अब \[ar\left( ACQ \right)\]और \[ar\left( APQ \right)\]की तुलना कीजिए।

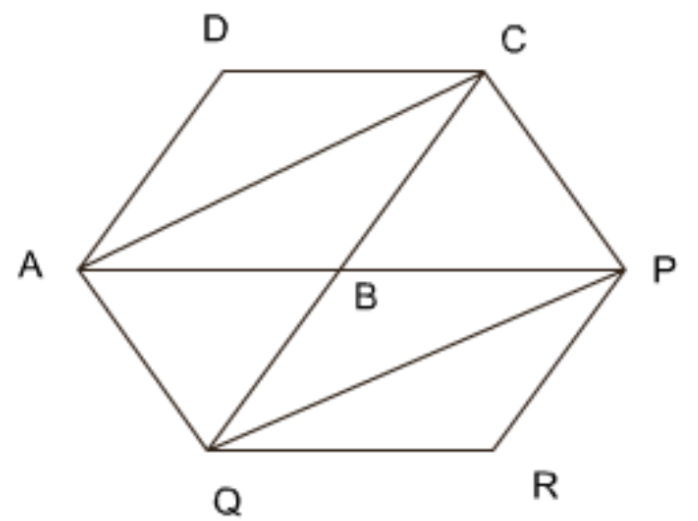
उत्तर: त्रिभुज \[ACQ\] और \[APQ\] में

दोनों त्रिभुज एक ही आधार \[AQ\] पर बने हुए हैं और समांतर रेखाओं \[AQ||CP\] के बीच हैं

इसलिए, \[ar\left( ACQ \right)\text{ }=\text{ }ar\left( APQ \right)\]

अब, \[ar\left( ACQ \right)\text{ }\text{ }ar\left( ABQ \right)\text{ }=\text{ }ar\left( APQ \right)\text{ }\text{ }ar\left( ABQ \right)\]

या, \[ar\left( ABC \right)\text{ }=\text{ }ar\left( PBQ \right)\]

समांतर चतुर्भुज \[ABCD\] का विकर्ण \[AC\] है

इसलिए\[,\text{ }ar\left( ABC \right)\text{ }=\dfrac{1}{2}~ar\left( ABCD \right)\]

समांतर चतुर्भुज \[BPRQ\] का विकर्ण \[QP\] है

इसलिए, \[ar\left( PBQ \right)\text{ }=~1212ar\left( BPRQ \right)\]

इसलिए\[,\text{ }ar\left( ABCD \right)\text{ }=\text{ }ar\left( BPRQ \right)\]सिद्ध हुआ!

10. एक समलंब \[\mathbf{ABCD}\] जिसमें \[\mathbf{AB}||\mathbf{DC}\] है, के विकर्ण \[\mathbf{A}C\] और \[\mathbf{BD}\] परस्पर \[\mathbf{O}\] पर प्रतिच्छेद करते हैं। दर्शाइए कि \[\mathbf{ar}\left( \mathbf{AOD} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{BOC} \right)\]है।

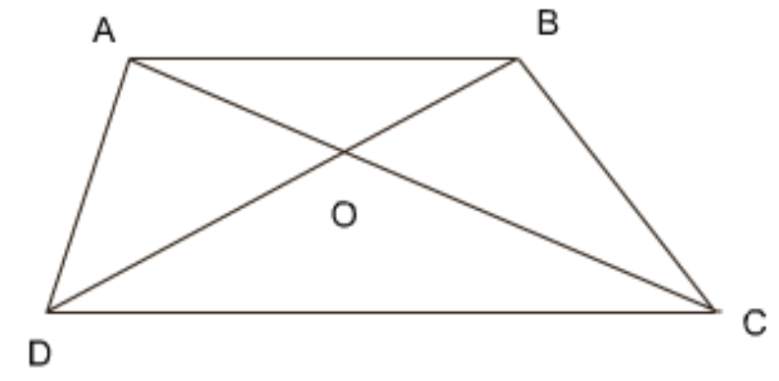
उत्तर: त्रिभुज \[DAC\] और \[CBD\] एक ही आधार और समांतर रेखाओं के बीच हैं

इसलिए\[,\text{ }ar\left( DAC \right)\text{ }=\text{ }ar\left( CBD \right)\]

अब, \[ar\left( DAC \right)\text{ }\text{ }ar\left( DOC \right)\text{ }=\text{ }ar\left( CBD \right)\text{ }\text{ }ar\left( DOC \right)\]

या, \[ar\left( AOD \right)\text{ }=\text{ }ar\left( BOC \right)\]सिद्ध हुआ!

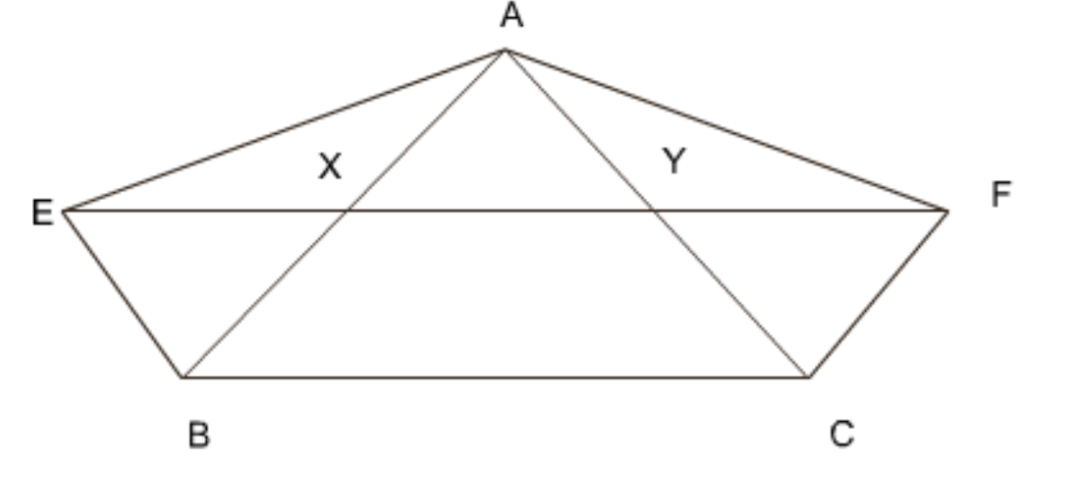
11. इस आकृति में \[\mathbf{ABCDE}\] एक पंचभुज है। \[\mathbf{B}\] से होकर \[\mathbf{AC}\] के समांतर खींची गई रेखा बढ़ाई गई \[\mathbf{DC}\] को \[\mathbf{F}\] पर मिलती है। दर्शाइए कि

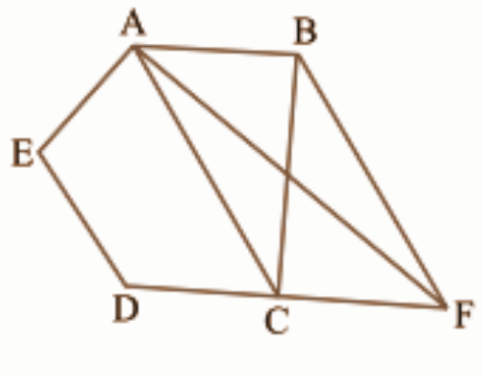
\[\begin{array}{*{35}{l}} i)\mathbf{ar}\left( \mathbf{ACB} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ACF} \right)  \\ ii)\mathbf{ar}\left( \mathbf{AEDF} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ABCDE} \right)  \\ \end{array}\]

उत्तर: त्रिभुज \[ACB\] और \[ACF\] समान आधार \[CF\] पर बने हैं और समान समांतर रेखाओं \[AC\] और \[BF\] के बीच बने हैं

इसलिए, \[ar\left( ACB \right)\text{ }=\text{ }ar\left( ACF \right)\]

अब, \[ar\left( ACB \right)\text{ }+\text{ }ar\left( ACDE \right)\text{ }=\text{ }ar\left( ACF \right)\text{ }+\text{ }ar\left( ACDE \right)\]

या, \[ar\left( ABCDE \right)\text{ }=\text{ }ar\left( AEDF \right)\] सिद्ध हुआ!

12. गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केंद्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबंध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव कि किस प्रकार कार्यांवित किया जा सकता है।

उत्तर: \[ABCD\] एक चतुर्भुज है। \[A\] को \[C\] से मिलाइए और \[BE||AC\] खींचिए जो \[DC\] को \[E\] तक बढ़ाने पर काटता है।

सिद्ध करना है: \[ar\left( ADE \right)\text{ }=\text{ }ar\left( ABCD \right)\]

\[BE||AC\]

इसलिए, \[AB\text{ }=\text{ }CE\]

\[ar\left( ACB \right)\text{ }=\text{ }ar\left( CAE \right)\] (समान आधार और समांतर भुजाओं के बीच बने त्रिभुज)

\[ar\left( ACB \right)\text{ }+\text{ }ar\left( ADC \right)\text{ }=\text{ }ar\left( CAE \right)\text{ }+\text{ }ar\left( ADC \right)\]

या, \[ar\left( ADE \right)\text{ }=\text{ }ar\left( ABCD \right)\]सिद्ध हुआ!

13. \[\mathbf{ABCD}\] एक समलंब है, जिसमें \[\mathbf{AB}\text{ }||\text{ }\mathbf{DC}\] है। \[\mathbf{AC}\] के समांतर एक रेखा \[\mathbf{AB}\] को \[\mathbf{X}\] पर और \[\mathbf{BC}\] को \[\mathbf{Y}\] पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि \[\mathbf{ar}\left( \mathbf{ADX} \right)\text{ }=\] \[\mathbf{ar}\left( \mathbf{ACY} \right)\]है। (संकेत: \[\mathbf{CX}\] को मिलाइए)

उत्तर: \[ABCD\] एक समलंब है जिसमें \[AB||DC\] तथा \[XY||AC\]

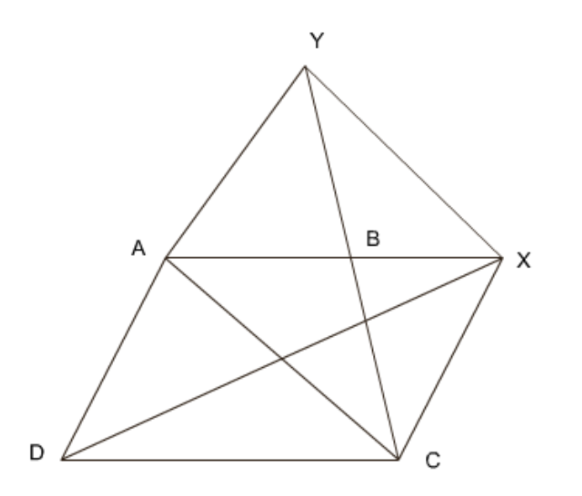
यहाँ: \[ar\left( ACY \right)\text{ }=\text{ }ar\left( ACX \right)\] (समान आधार और समांतर भुजाओं के त्रिभुज)

\[ar\left( ADX \right)\text{ }=\text{ }ar\left( ACX \right)\] (समान आधार और समांतर भुजाओं के त्रिभुज)

इसलिए, \[ar\left( ADX \right)\text{ }=\text{ }ar\left( ACY \right)\]सिद्ध हुआ!

14. इस आकृति में \[\mathbf{AP}\text{ }\left| \left| \text{ }\mathbf{BQ}\text{ } \right| \right|\mathbf{CR}\] है। सिद्ध कीजिए कि \[\mathbf{ar}\left( \mathbf{AQC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{PBR} \right)\]है।

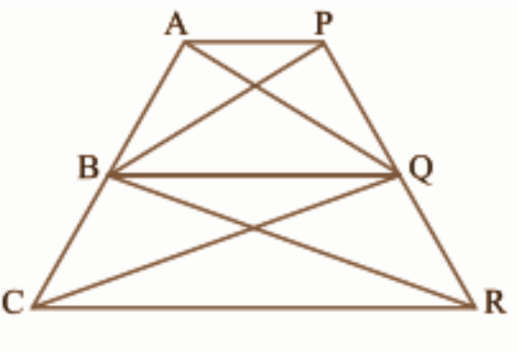
उत्तर: \[ar\left( ABQ \right)\text{ }=\text{ }ar\left( PBQ \right)\] (समान आधार और समांतर भुजाओं के त्रिभुज)

\[ar\left( BQC \right)\text{ }=\text{ }ar\left( RBQ \right)\] (समान आधार और समांतर भुजाओं के त्रिभुज)

इसलिए, \[ar\left( ABQ \right)\text{ }+\text{ }ar\left( BQC \right)\text{ }=\text{ }ar\left( PBQ \right)\text{ }+\text{ }ar\left( RBQ \right)\]

या, \[ar\left( AQC \right)\text{ }=\text{ }ar\left( PBR \right)\]सिद्ध हुआ!

15. चतुर्भुज \[\mathbf{ABCD}\] के विकर्ण \[\mathbf{AC}\] और \[\mathbf{BD}\] परस्पर बिंदु \[\mathbf{O}\] पर इस प्रकार प्रतिच्छेद करते हैं कि ar(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलंब है।

उत्तर: \[:~ar\left( AOD \right)\text{ }=\text{ }ar\left( BOC \right)\] (दिया गया है)

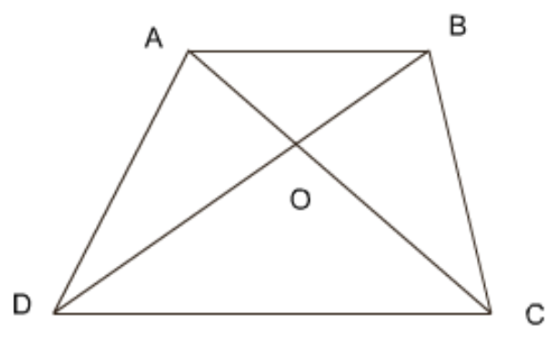
\[ar\left( AOD \right)\text{ }+\text{ }ar\left( DOC \right)\text{ }=\text{ }ar\left( BOC \right)\text{ }+\text{ }ar\left( DOC \right)\]

या, \[ar\left( ADC \right)\text{ }=\text{ }ar\left( BDC \right)\]

इसलिए, \[AB||DC\]

इसलिए यह सिद्ध हुआ कि \[ABCD\] एक समलंब है।

16. इस आकृति में \[\mathbf{ar}\left( \mathbf{DRC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{DPC} \right)\]है और\[\mathbf{ar}\left( \mathbf{BDP} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ARC} \right)\]है। दर्शाइए कि दोनों चतुर्भुज \[\mathbf{ABCD}\] और \[\mathbf{DCPR}\]समलंब हैं।

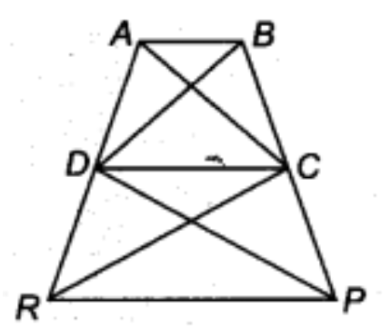
उत्तर: \[ar\left( DRC \right)\text{ }=\text{ }ar\left( DPC \right)\] (दिया गया है)

इसलिए, \[DC||RP\]

इसलिए, \[DCPR\] एक समलंब है

अब, \[ar\left( BDP \right)\text{ }=\text{ }ar\left( ARC \right)\] (दिया गया है)

या\[,\text{ }ar\left( BDP \right)\text{ }\text{ }ar\left( DPC \right)\text{ }=\text{ }ar\left( ARC \right)\text{ }\text{ }ar\left( DRC \right)\]

या, \[ar\left( ADC \right)\text{ }=\text{ }ar\left( BDC \right)\]

इसलिए, \[AB||DC\]

इसलिए, \[ABCD\] एक समलंब है।

प्रश्नावली 9.4

1. समांतर चतुर्भुज \[\mathbf{ABCD}\] और आयत \[\mathbf{ABEF}\] एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।

उत्तर: इस आकृति में, \[ABCD\] एक समांतर चतुर्भुज है और \[EFCD\] एक आयत है। दोनों एक ही आधार \[DC\] पर बने हुए हैं।

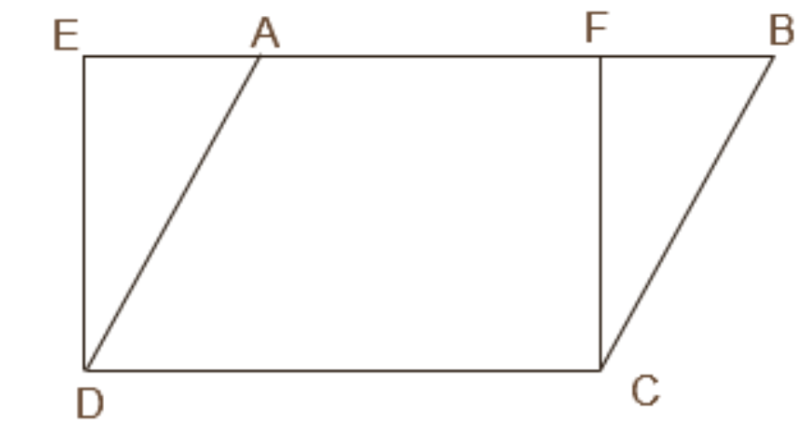
समांतर चतुर्भुज की ऊँचाई\[=FC\]

\[AB\text{ }=\text{ }DC\] (समांतर चतुर्भुज की सम्मुख भुजाएँ)

\[EF\text{ }=\text{ }DC\] (आयत की सम्मुख भुजाएँ)

इन दो समीकरणों से यह साफ है कि

\[EF\text{ }=\text{ }DC\]

यानि \[EA\text{ }=\text{ }FB\]

\[ABCD\] का परिमाप\[=AB\text{ }+\text{ }BC\text{ }+\text{ }CD\text{ }+\text{ }AD\]

\[EFCD\] का परिमाप \[=EF\text{ }+\text{ }FC\text{ }+\text{ }CD\text{ }+\text{ }ED\]

\[=\text{ }AB\text{ }+\text{ }CD\text{ }+\text{ }FC\text{ }+\text{ }ED\]

\[\Delta EAD\] में

\[AD\text{ }>\text{ }ED\] (कर्ण सबसे लंबी भुजा होती है)

\[\Delta FBC\] में

\[BC\text{ }>\text{ }FC\] (कर्ण सबसे लंबी भुजा होती है)

इसलिए, \[AB\text{ }+\text{ }CD\text{ }+\text{ }BC\text{ }+\text{ }AD\text{ }>\text{ }AB\text{ }+\text{ }CD\text{ }+\text{ }FC\text{ }+\text{ }ED\]

इससे यह सिद्ध होता है कि एक ही आधार पर बने समांतर चतुर्भुज और आयत में से समांतर चतुर्भुज का परिमाप अधिक होता है।

2. इस आकृति में भुजा \[\mathbf{BC}\] पर दो बिंदु \[\mathbf{D}\] और \[\mathbf{E}\] इस प्रकार स्थित हैं कि \[\mathbf{BD}\text{ }=\text{ }\mathbf{DE}\text{ }=\text{ }\mathbf{EC}\] है। दर्शाइए कि \[\mathbf{ar}\left( \mathbf{ABD} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{ADE} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{AEC} \right)\]है।

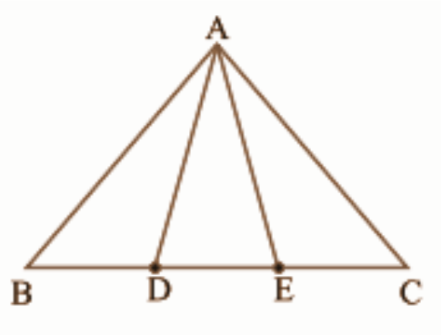
क्या आप अब इस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है”?

उत्तर: \[\Delta ABD,\text{ }\Delta ADE\] और \[\Delta AEC\] इन सबकी ऊँचाई \[=h\]

\[BD\text{ }=\text{ }DE\text{ }=\text{ }EC\] (दिया गया है)

इसलिए आधार समान हैं

इसलिए हर त्रिभुज का क्षेत्रफल \[=~\dfrac{1}{2}\times h\times b\]

इसलिए\[,\text{ }ar\left( ABD \right)\text{ }=\text{ }ar\left( ADE \right)\text{ }=\text{ }ar\left( AEC \right)\]सिद्ध हुआ

3. इस आकृति में \[\mathbf{ABCD},\text{ }\mathbf{DCFE}\] और \[\mathbf{ABFE}\] समांतर चतुर्भुज हैं। दर्शाइए कि \[\mathbf{ar}\left( \mathbf{ADE} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{BCF} \right)\]है।

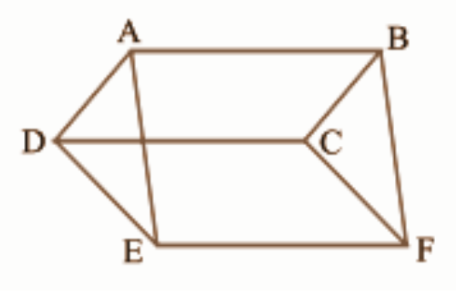
उत्तर: \[\Delta ADE\] और \[\Delta \text{ }BCF\] में

\[AE\text{ }=\text{ }BF\] (समांतर चतुर्भुज \[ABFE\] की सम्मुख भुजाएँ)

\[AD\text{ }=\text{ }BC\] (समांतर चतुर्भुज \[ABCD\] की सम्मुख भुजाएँ)

\[DE\text{ }=\text{ }CF\] (समांतर चतुर्भुज \[DCFE\] की सम्मुख भुजाएँ)

इसलिए \[SSS\] प्रमेय के अनुसार

\[\Delta ADE\cong \Delta \text{ }BCF\]

या, \[ar\left( \Delta ADE \right)\text{ }=\text{ }ar\left( \Delta \text{ }BCF \right)\]सिद्ध हुआ!

4. इस आकृति में \[\mathbf{ABCD}\] एक समांतर चतुर्भुज है और \[\mathbf{BC}\] को एक बिंदु \[\mathbf{Q}\] तक इस प्रकार बढ़ाया गया है \[\mathbf{AD}\text{ }=\text{ }\mathbf{CQ}\] है। यदि \[\mathbf{AQ}\] भुजा \[\mathbf{DC}\] को \[\mathbf{P}\] पर प्रतिच्छेद करती है तो दर्शाइए कि \[\mathbf{ar}\left( \mathbf{BPC} \right)\text{ }=\text{ }\mathbf{ar}\left( \mathbf{DPQ} \right)\]है। (संकेत: \[\mathbf{AC}\] को मिलाइए)

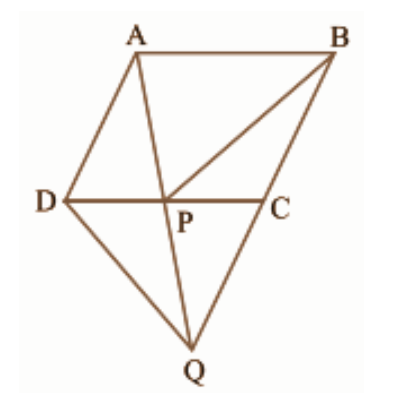
उत्तर: \[AD\text{ }=\text{ }CQ\] (दिया गया है)

\[AD\text{ }=\text{ }BC\] (समांतर चतुर्भुज \[ABCD\] की सम्मुख भुजाएँ)

इसलिए, \[AD\text{ }=\text{ }CQ\text{ }=\text{ }BC\]

\[ar\left( \Delta QAC \right)\text{ }=\text{ }ar\left( \Delta QDC \right)\] 

(एक ही आधार \[QC\] और समांतर रेखाओं \[DA\] और \[QC\] के बीच के त्रिभुज)

दोनों तरफ से \[\Delta QPC\] घटाने पर

\[ar\left( \Delta QAC\text{ }-\text{ }\Delta QPC \right)\text{ }=\text{ }ar\left( \Delta QDC\text{ }-\text{ }\Delta QPC \right)\]

\[\text{ }ar\left( \Delta APC \right)\text{ }=\text{ }ar\left( \Delta DPQ \right)\text{ }\ldots \ldots \ldots ..\left( 1 \right)\]

अब, \[ar\left( \Delta PAC \right)\text{ }=\text{ }ar\left( \Delta PBC \right)\text{ }\ldots \ldots \ldots ..\left( 2 \right)\]

(एक ही आधार \[PC\] समांतर रेखाओं \[AB\] और \[PC\] के बीच के त्रिभुज)

समीकरण \[(1)\]और \[(2)\]से

\[ar\left( \Delta BPC \right)\text{ }=\text{ }ar\left( \Delta DPQ \right)\text{ }\]इति सिद्धम!

NCERT Solutions for Class 9 Maths Chapter 9 Area of Parallelograms and Triangles in Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 9 Maths Chapter 9 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 9 Maths Chapter 9 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 9 Maths Chapter 9 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 9 Maths Area of Parallelograms and Triangles solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 9 Maths Area of Parallelograms and Triangles in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 9 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 9 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.