NEET Important Chapter- Mechanical Properties of Solids

The chapter Mechanical properties of solids is one of the easiest chapters in physics as far as the NEET exam is concerned. As the name of the chapter implies, we deal with the properties of solids and their behaviour under applied stress and some concept-oriented problems from this chapter.

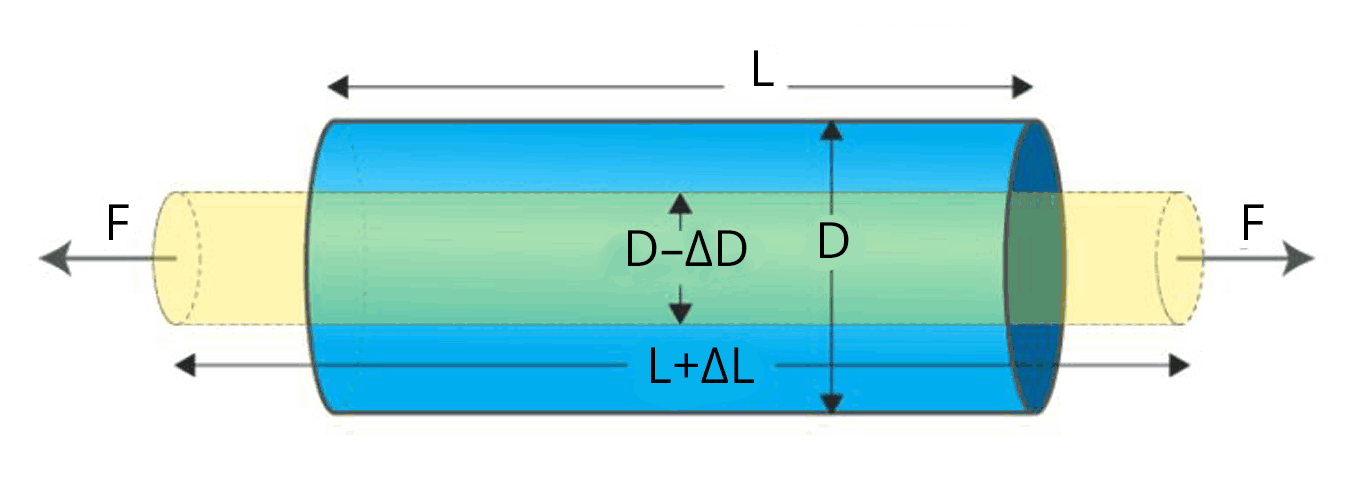
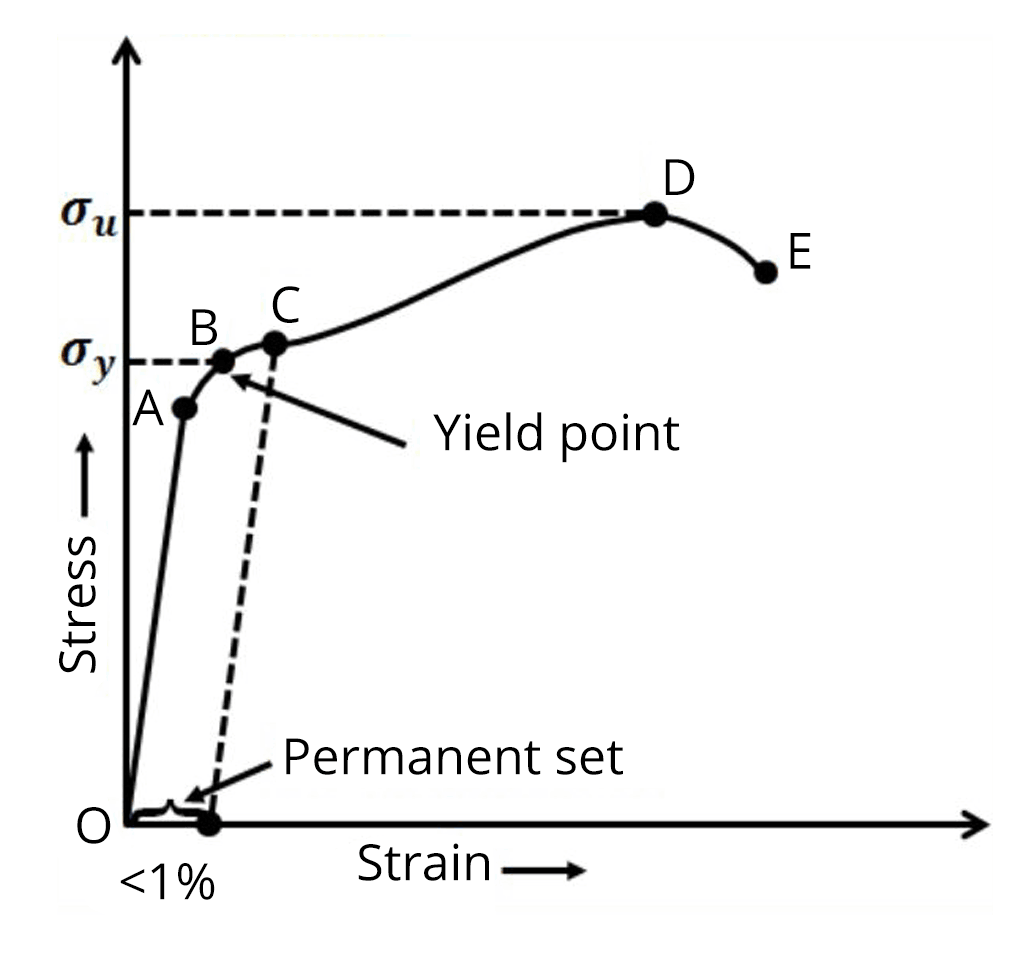
In the chapter Mechanical properties of solids, first, we will learn about different types of stress like longitudinal stress and  bulk stress along with different types of strain. The stress-strain curve of a wire under longitudinal stress is studied in detail. Hooke's law and types of modulus of elasticity are very important in this chapter. Problems related to young’s modulus, bulk modulus and rigidity modulus are discussed in this chapter. 

Let us see the important concepts, mechanical properties of solids formulas in this chapter Mechanical properties of solids needed for the  NEET exam with solved mechanical properties of solids numerical examples.

Mechanical Properties of Solids- Important Topics 

• Elastic behaviour of solids

• Longitudinal stress and Longitudinal strain

• Volume stress and volume strain 

• Volume stress and volume strain 

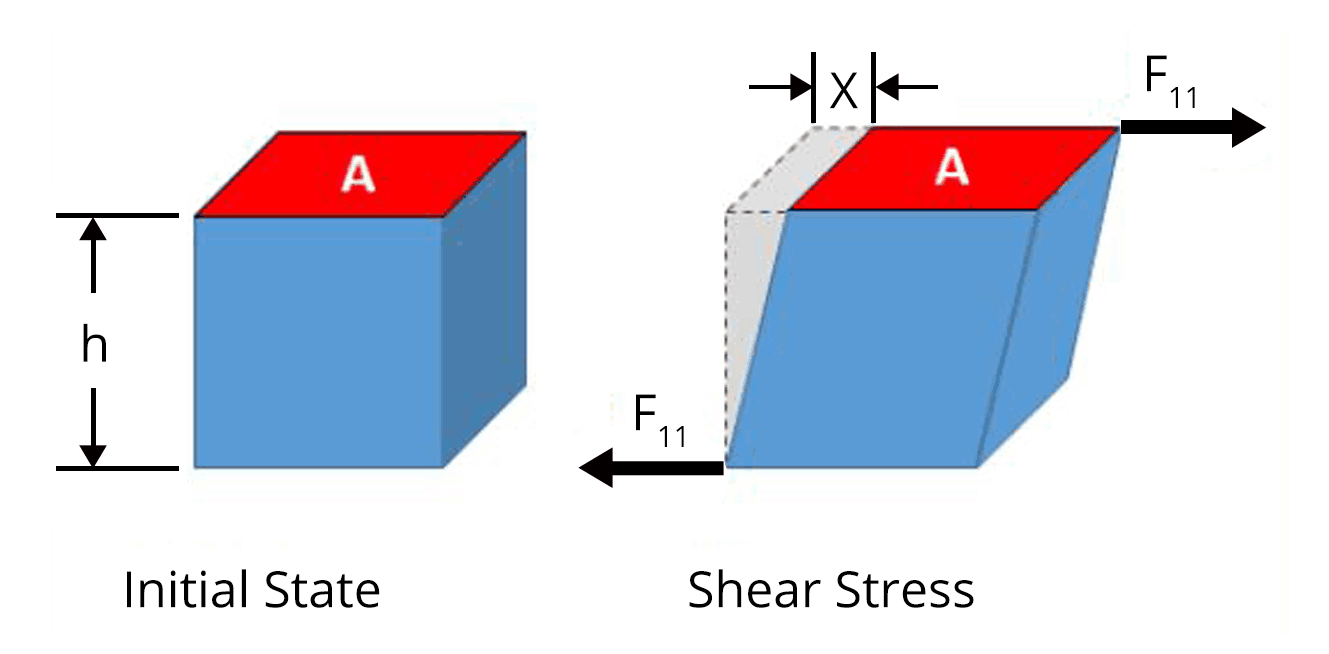
• Shear or tangential stress or shearing strain

• Young’s modulus

• Bulk modulus

• Modulus of rigidity

• Work done in stretching a strain

Important Concepts of Mechanical Properties of Solids

Name of the Concept	Key Points of the Concept
Elastic behaviour of solids	When a deforming force is applied to a body, it changes its shape or size. Elasticity is the ability to regain its original shape and size even after deforming force is removed. When deforming force is applied, atoms are displaced from their equilibrium position and return back to the initial position due to interatomic forces after deforming force is removed. The restoring force acting per unit area of cross-section of deformed force is called stress having unit N/m2. The strain is the ratio of change in dimension to the original dimension when the deforming force is applied. $\text{stress}=\dfrac{\text{Force}}{\text{Area}}$ Plasticity is the ability of a body to undergo permanent deformation even after deforming force is removed.
Longitudinal stress and Longitudinal strain	When a deforming force is applied parallel to the length of a rod, its length increases and the stress developed is called longitudinal stress or tensile stress. It occurs in solids only. Longitudinal strain is the ratio of change in length to the original length due to longitudinal stress. $\text{Longitudinal strain}=\dfrac{\text{change in length}}{\text{original length}}$ $\text{Longitudinal strain}=\dfrac{\Delta l}{l}$
Volume stress and volume strain	Due to volume stress or bulk stress, the volume and density of the body but the shape remains the same.   (Image will be uploaded soon) The deforming force applied is normal to the surface at all points. Bulk stress occurs in solids, liquids and gases. Volume strain is the ratio of change in volume to the original volume given by the formula, $\text{Volume strain}=\dfrac{\text{change in volume}}{\text{original volume}}$ $\text{Longitudinal strain}=\dfrac{\Delta V}{V}$
Shear or tangential stress or shearing strain	Tangential stress or shear stress is developed when the deforming force is applied tangentially to the surface. Due to shearing stress, there is the relative displacement between successive layers Shearing strain is defined as the angle in radians through which the vertical surface gets turned due to tangential force and its formula is given by, $\text{Shearing strain}=\dfrac{\text{x}}{h}$
Strain-strain curve	Stress-strain shows the behaviour of the wire with an increase in load. In the region from O to A, the curve is linear and obeys’ Hooke's law. The point A is called the proportional limit. According to Hooke's law, stress is proportional to strain within the proportional limit. The wire shows elastic behaviour up to point B and point B is called the yield point or elastic limit. The stress corresponding to the yield point is called yield strength. Beyond point B, it loses its elastic behaviour and does not regain its original length even after deforming force is removed. The stress corresponding to point  D is called ultimate strength.
Young’s modulus	Young’s modulus is the ratio of longitudinal stress to the longitudinal strain. $\text{Young's modulus}=\dfrac{\text{Longitudinal stress}}{\text{longitudinal strain}}$ $\text{Young's modulus}=\dfrac{F/A}{\Delta l/l}$
Bulk modulus	Bulk modulus is the ratio of normal stress to the volume strain given by the formula, $\text{Bulk modulus}=\dfrac{\text{Normal stress}}{\text{Volumetric strain}}$ $\text{Bulk modulus}=\dfrac{F/A}{-\Delta V/V}$ $\text{Bulk modulus}=\dfrac{-PV}{\Delta V}$
Modulus of rigidity	Within the limits of proportionality, the ratio of tangential stress to the shearing strain is called modulus of rigidity $\text{Rigidity modulus}=\dfrac{\text{shearing stress}}{\text{shearing strain}}$ $\eta=\dfrac{F/A}{\text{x/h}}$
Work done in stretching a strain	Work done in stretching a wire having young’s modulus(Y) under a force (F) is given by the formula, $W=\dfrac{1}{2}\dfrac{YA\Delta l^2}{l}$

List of Important Formulae

Solved Examples 

1. A long elastic spring is stretched by 2 cm and its potential energy is U. If the spring is stretched by 10 cm, then the  P.E will be,

a. U

b. 98U/5

c. 3U

d. 25U

Ans:  

Given, Potential energy of spring stretched by 2 cm = U

$U=\dfrac{1}{2}K(2~cm)^2$....(1)

The potential energy of the spring stretched by 10 cm can be calculated using the formula given by,

$U'=\dfrac{1}{2}K(10~cm)^2$....(2)

Divide equation (2) by equation (1) to calculate the potential energy of the spring stretched by 10 cm

$\dfrac{U'}{U}=\dfrac{\dfrac{1}{2}K(10~cm)^2}{\dfrac{1}{2}K(2~cm)^2}$

$U'=25U$

Therefore, the correct answer is option d).

Key point: The potential energy of the spring depends on the spring constant and the elongation. 

2. A cube of aluminium of 0.1 m is subjected to a shearing force of 100 N? The top face of the cube is displaced through 0.02 cm with respect to the bottom face. The shearing strain will be

Ans: Given,

The height of the cube, h = 0.1 m = 10 cm

The displacement of the top face due to the tangential force of 100 N, x = 0.02 cm

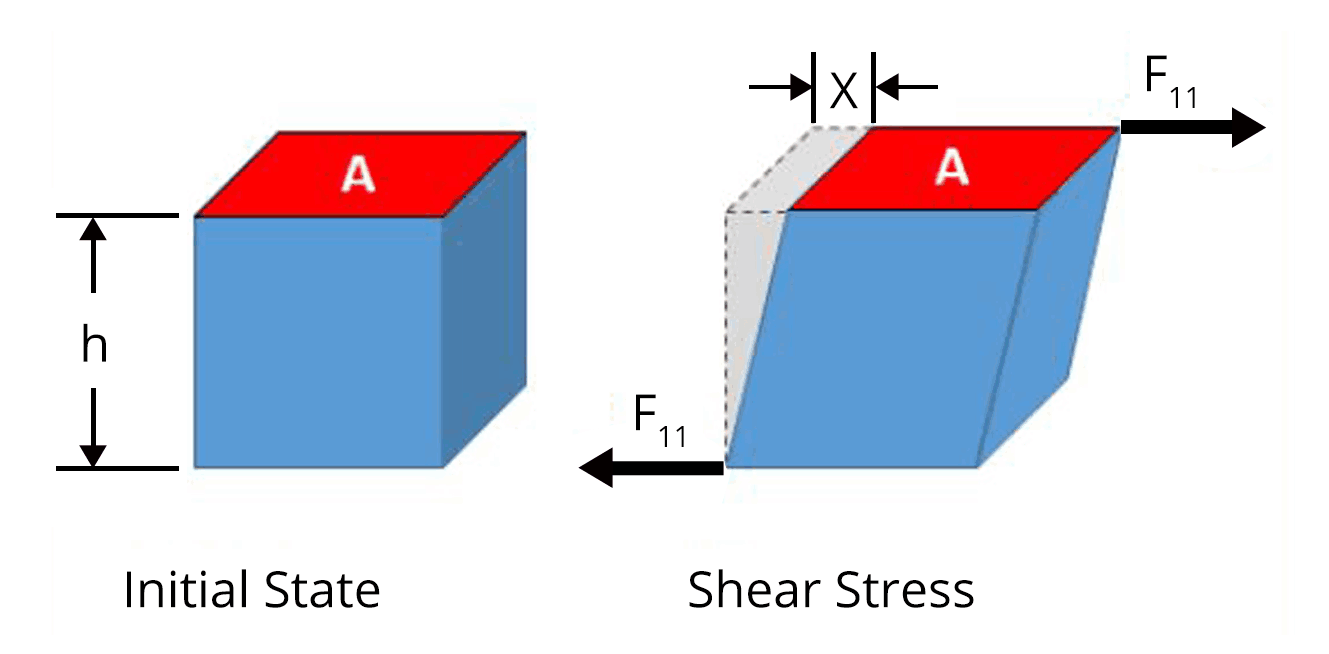
The shearing strain can be calculated using the formula,

$\text{Shearing strain}=\dfrac{\text{x}}{h}$ 

$\text{Shearing strain}=\dfrac{\text{0.02 cm}}{10 \text{ cm}}$ 

$\text{Shearing strain}=0.002$

Key point:  Shearing strain is equal to the ratio of displacement of the top face to the  height of the cube.    

Previous Year Questions from NEET paper

1. When a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L+l). The elastic potential energy stored in the extended  wire is (NEET 2019)

a. Mgl

b. 2Mgl

c. Mgl/2

d. Mgl/4 

Ans: 

The force acting on the wire is related to the extension of the wire 

$F=Kl$

$K=\dfrac{F}{l}$

$K=\dfrac{Mg}{l}$....(1)

The energy stored in the wire is given by,

$U=\dfrac{1}{2}Kl^2$....(2)

Put equation (1) in equation (2)

$U=\dfrac{1}{2}\dfrac{Mg}{l}l^2$

$U=\dfrac{1}{2}Mgl$

Therefore, the correct answer is option C.

Key point:  When a wire is suspended by a mass, then weight acting on the mass acts as the deforming force.

2. The bulk modulus of a spherical object is ‘B’. If it is subjected to uniform pressure ‘p’, the fractional decrease in radius will be  (NEET 2017)

a. B/3p

b. 3p/B

c. p/3B

d. p/B

Ans:

The fraction volume of a spherical object having radius r is given by,

$V=\dfrac{4\pi r^3}{3}$

$\dfrac{\Delta V}{V}=3\dfrac{\Delta r}{r}$...(1)

The formula to calculate the bulk modulus is given by,

$B=\dfrac{p}{\Delta V/V}$

${\Delta V/V}=\dfrac{p}{B}$...(2)

Put equation(1) in equation (2) to calculate the fractional decrease in radius

${3\dfrac{\Delta r}{r}}=\dfrac{p}{B}$

${\dfrac{\Delta r}{r}}=\dfrac{p}{3B}$

Key point:  Fractional decrease in radius can be obtained from the formula for the volume of the sphere.

Practice Questions

1. If the volume of the wire remains constant when subjected to tensile stress, then the value of Poisson's ratio of the material of the wire is, 

(Ans: 0.5 )

2. What increase in pressure is required to decrease the volume of 200 litres of water by 0.004 per cent? Given bulk modulus of water is 2100 MPa 

(Ans: 84 KPa)

Conclusion

In this article, we discussed important topics, and important formulas  in the mechanical properties of solids chapter from the NEET point of view. Students must make sure that they do not miss any of the above important topics to obtain a good score on the NEET  exam.