The Solid State Class 12 Notes NEET Chemistry (Free PDF Download)

Introduction

Apart from liquid and gaseous states, a solid-state is a state of matter. Solids have very strong intermolecular interactions, and there are very few vacant spaces between the atoms/ions/molecules. As a result, they have a predetermined shape and volume.

Characteristic Properties of Solids

The following properties come under the category of solids:

• Solids have high density.

• Solids have low compressibility.

• Solids are rigid in nature.

• Solids have definite shape and volume.

Classification of Solids:

On the basis of the following parameter, solids are broadly classified as:

• Classification based on various properties.

• Classification based on bonding present in building blocks.

On the basis of various properties:

On the basis of the various properties of solids, they can be classified as:

• Crystalline solids

• Amorphous solids

Amorphous solids have an uneven structure over long distances and lack sharp properties, whereas crystalline solids have a regular structure throughout the entire volume and sharp qualities. 

The table below shows the many differences.

Based on bonding

Solids are classified according to the sort of bonding present in their building units. The table below lists many types of solids as well as their properties. 

The different properties of the four types of solids are listed as:

Structure Of Crystalline Solids

Crystal Lattice and Unit Cell

The crystalline solid regular array of building pieces (atoms/ions/molecules) is known as the "Crystal Lattice."

"Unit Cell" refers to the smallest component of a crystal lattice that can be repeated in all directions to form the full crystal lattice.

Small spheres represent the atoms of ions or molecules in a unit cell. Variations in the following parameters produce several lattices:

• The edge along the 3 axis – a, b, c.

• The interfacial angle - \[{{\alpha , \beta , \gamma }}\] 

• Location of atoms/ions with respect to each other in crystal lattice.

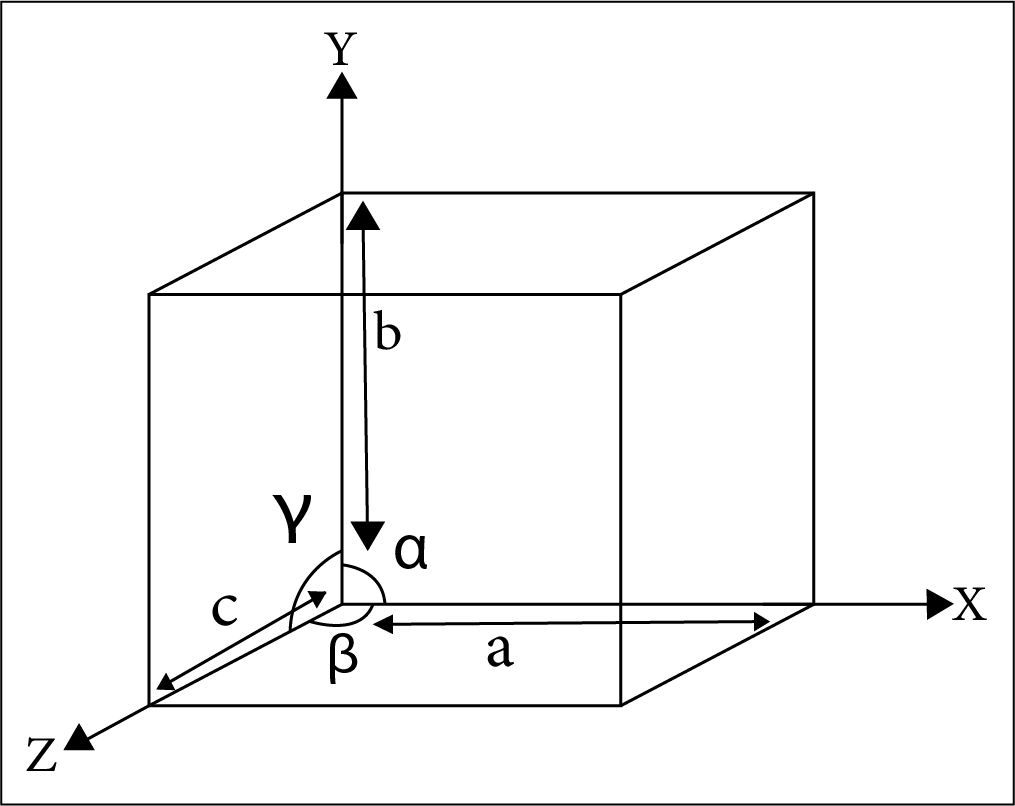
The Interfacial Angle Alpha Beta Gamma

Primitive Unit Cells and Bravais Lattices

There are seven different types of unit cells, as well as various subtypes of unit cells. Primitive Unit Cells or Crystal Habits are the names given to these seven unit cells. The following are listed in the table below:

For these 7 types of unit cells, 14 types of Lattices exist in nature. These 14 lattices are named as “Bravais Lattices”.

Crystal System			Space Lattice				Examples
Cubic ${\text{a}} = {\text{b}} = {\text{c}}$ Here a, b and c are the dimensions of a unit cell along three axes.  ${{\alpha }} = {{\beta }} = {{\gamma }} = {90^ \circ }$  Here, ${{\alpha }}$, ${{\beta }}$ and ${{\gamma }}$ are the sizes of three angles between the axes.	Simple: Lattice points at the eight corners of the unit cells.	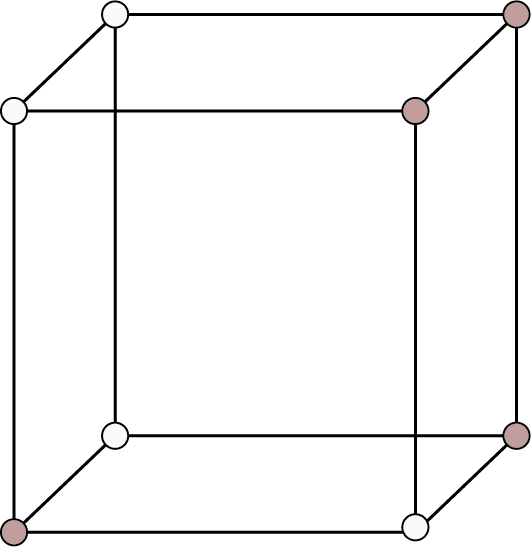	Body Centered: Points at the eight corners and at the body centre.	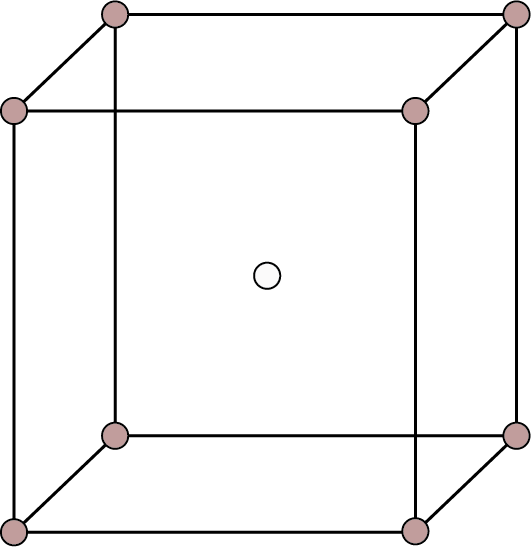	Face Centered: Points at the eight corners and at the six face enters.	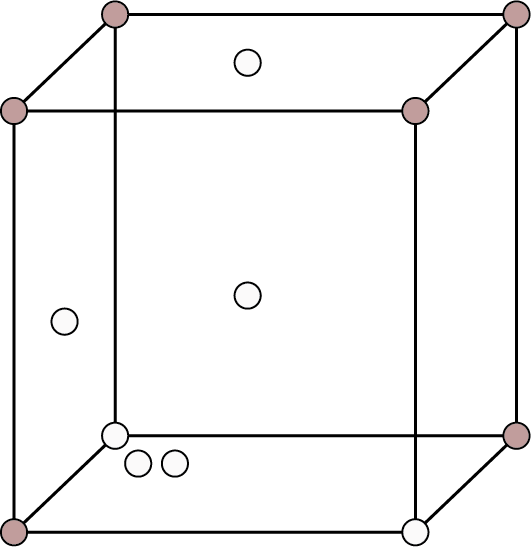	${\text{Pb, Hg, Ag}}$ ${\text{Au, Cu, ZnS}}$  Diamond, ${\text{KCl}}$ ${\text{NaCl}}$, ${\text{C}}{{\text{u}}_{\text{2}}}{\text{O}}$ , ${\text{Ca}}{{\text{F}}_{\text{2}}}$ and alumns, etc.
Tetragonal ${\text{a}} = {\text{b}} \ne {\text{c}}$  ${{\alpha }} = {{\beta }} = {{\gamma }} = {90^ \circ }$	Simple: Points at the eight corners of the unit cell.	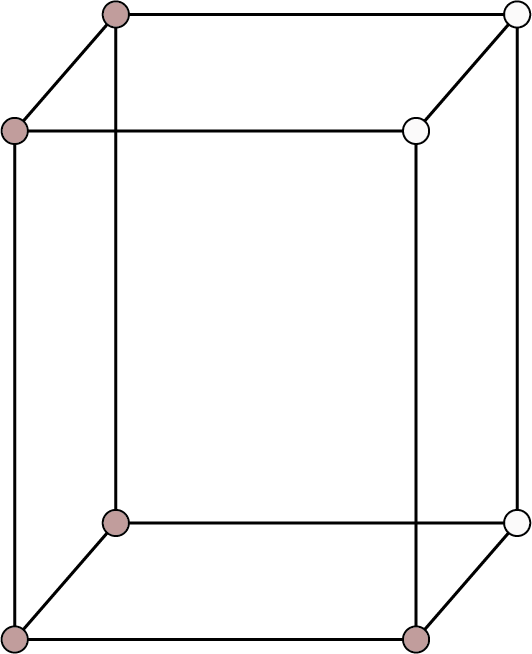	Body Centered: Points at the eight corners and at the body centre.	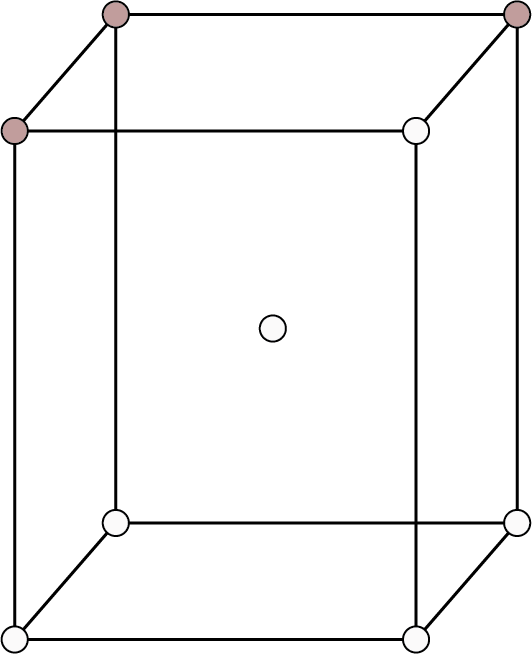			${\text{Sn}}{{\text{O}}_{\text{2}}}{\text{,Ti}}{{\text{O}}_{\text{2}}}{\text{,}}$   ${\text{Zn}}{{\text{O}}_{\text{2}}}{\text{,NiS}}{{\text{O}}_{\text{4}}}$   ${\text{ZrSi}}{{\text{O}}_{\text{4}}}{\text{,}}$   ${\text{PbW}}{{\text{O}}_{\text{4}}}$ And white tin.
Orthorhombic: ${\text{a}} \ne {\text{b}} \ne {\text{c}}$  ${{\alpha }} = {{\beta }} = {{\gamma }} = {90^ \circ }$	Simple: Points at the eight corners of the unit cell.	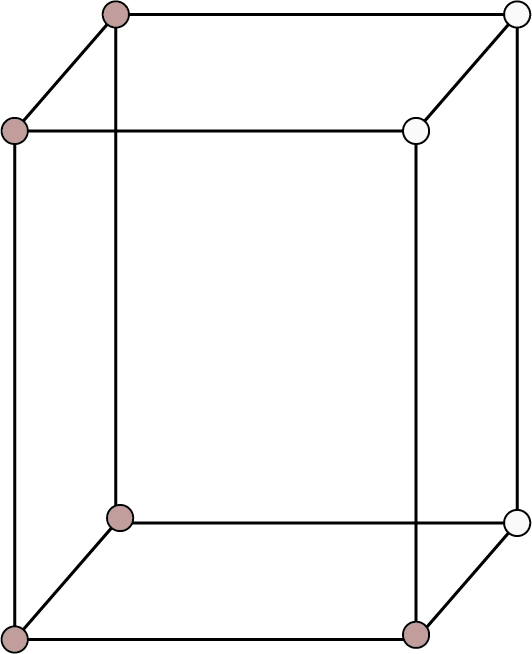End Centered: Also called side centered or base centered. Points at the eight corners and at two face centers opposite to each other.	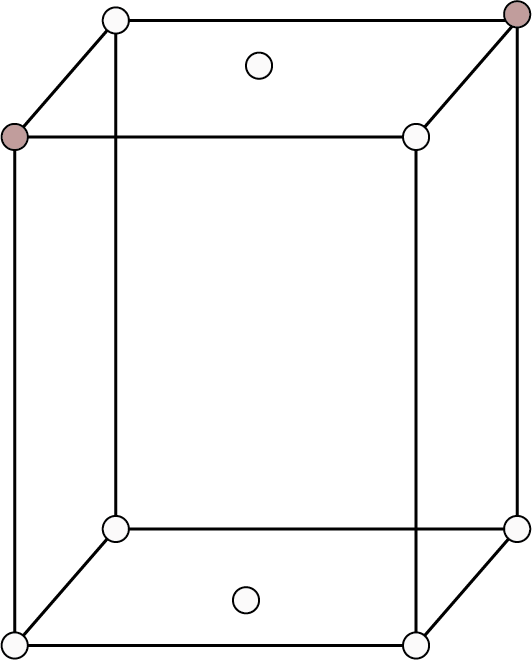	Body Centered: Points at the eight corners and at the body centre.		Face Centered: Points at the eight corners and at the six face centres. (Image will be uploaded soon)	${\text{KN}}{{\text{O}}_{\text{3}}}{\text{, }}{{\text{K}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}}{\text{,}}$   ${\text{PbC}}{{\text{O}}_{\text{3}}}{\text{, BaS}}{{\text{O}}_{\text{4}}}$ Rhombic sulphur, ${\text{MgS}}{{\text{O}}_{\text{4}}}{\text{.7}}{{\text{H}}_{\text{2}}}{\text{O}}$ etc.
Rhombohedral or Trigonal  ${\text{a}} = {\text{b}} = {\text{c}}$ , ${{\alpha }} = {{\beta }} = {{\gamma }} \ne {90^ \circ }$	Simple: Points at the edge corners of the unit cell.						${\text{NaN}}{{\text{O}}_{\text{3}}}{\text{, CaS}}{{\text{O}}_{\text{4}}}$ , calcite, quartz, ${\text{As, Sb, Bi}}$
Hexagonal ${\text{a}} = {\text{b}} \ne {\text{c}}$ , ${{\alpha }} = {{\beta }} = {90^ \circ }$   ${{\gamma }} = {120^ \circ }$	Simple: Points at the twelve or points at the twelve corners of the unit cell out corners of the hexagonal lined by thick line, prism and at the centres of top and bottom faces.						${\text{ZnO, PbS, CdS}}$ , graphite, ice, ${\text{Mg, Zn, Cd}}$ etc.
Monoclinic ${\text{a}} \ne {\text{b}} \ne {\text{c}}$  ${{\alpha }} = {{\gamma }} = {90^ \circ }$ , ${{\beta }} \ne {90^ \circ }$	Simple: Points at the eight corners of the unit cell.			End Centered: Point at the eight corners and two face centres opposite to each other.			${\text{N}}{{\text{a}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}}{\text{.10}}{{\text{H}}_{\text{2}}}{\text{O}}$ , ${\text{N}}{{\text{a}}_{\text{2}}}{{\text{B}}_{\text{4}}}{{\text{O}}_{\text{7}}}{\text{.10}}{{\text{H}}_{\text{2}}}{\text{O}}$ , ${\text{CaS}}{{\text{O}}_{\text{4}}}{\text{.2}}{{\text{H}}_{\text{2}}}{\text{O}}$ , monoclinic sulphur etc.
Triclinic ${\text{a}} \ne {\text{b}} \ne {\text{c}}$  ${{\alpha }} \ne {{\beta }} \ne {{\gamma }} \ne {90^ \circ }$	Simple: Points at eight corners of the unit cell.	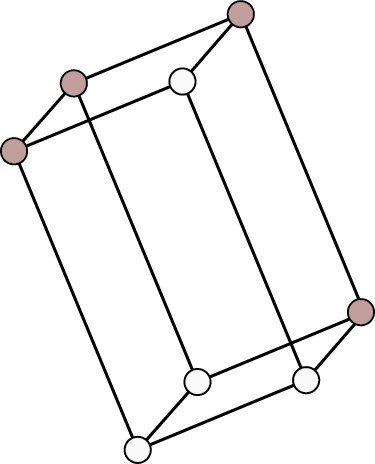					${\text{CaS}}{{\text{O}}_{\text{4}}}{\text{.5}}{{\text{H}}_{\text{2}}}{\text{O}}$ , ${{\text{K}}_{\text{2}}}{\text{C}}{{\text{r}}_{\text{2}}}{{\text{O}}_{\text{7}}}$ , ${{\text{H}}_{\text{3}}}{\text{B}}{{\text{O}}_{\text{3}}}$

The focus will primarily be on cubic unit cells and their arrangements.

Cubic Unit Cells

The most common unit cell is this one. The atoms or spheres in a cubic unit cell can be found at the following locations.

• Corners

• Body centre

• Face centres

The contributions of a sphere stored at various locations are as follows:

Types of Cubic Unit Cells

Cubic Unit Cells

The following factors distinguish these unit cells from one another:

• The positions of the spheres within the unit cell.

• The unit cell's rank (effective number of spheres inside a unit cell).

• The relationship between the radius and the edge length of a single sphere.

• Fractional packing (fraction of volume occupied by spheres in a unit cell).

The following parameters are provided in the table below for all three unit cells:

Type of Cubic Crystal	No. of atoms at different locations			Structure	Rank	Packing	Relation b/w atomic radius and edge length (a)
	Corners	Body Centres	Face Centre
Simple Cubic	8	-	-		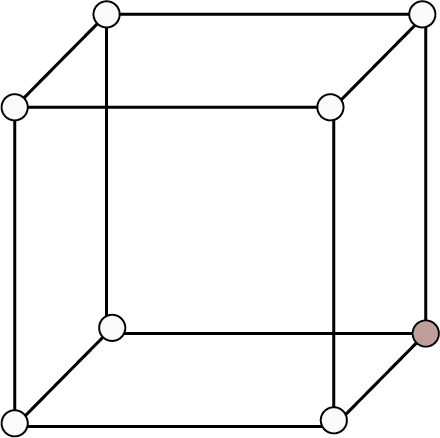1	52%	r = a/2
Body Centred	8	1	-		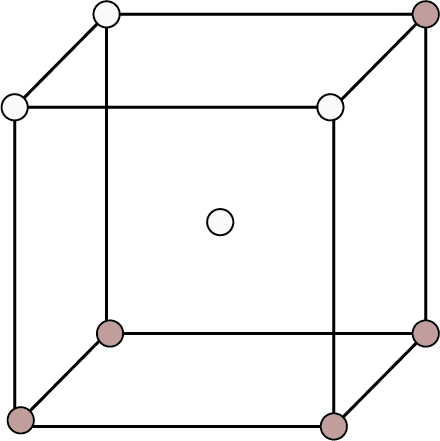2	68%	${\text{r}} = \dfrac{{\sqrt {3{\text{a}}} }}{4}$
Face Centred	8	-	6		4	74%	${\text{r}} = \dfrac{{\sqrt {2{\text{a}}} }}{4}$

Density of Cubic Crystals

By the following formula, the density of the cubic crystal is given:

${\text{\rho }} = \dfrac{{{\text{M}} \times {\text{Z}}}}{{{{\text{a}}^{\text{3}}} \times {{\text{N}}_{\text{A}}}}}$ 

Where, Z is the rank of the unit cell, M is the molar mass of the solid, a is the edge length of the unit cell, NA is the Avogadro number.

The volume of Z will depend on the type of unit cell.

Close packing in solids: Origin of unit cells

Assume we have a set of spheres of identical size that we must arrange in a single layer with the requirement that the spheres be in close proximity to one another. There are two sorts of layers that can be used:

• Square Packing

• Hexagonal Packing

Spheres are arranged in square packing in such a way that the rows are both horizontal and vertical. The Coordination number is 4 in this situation.

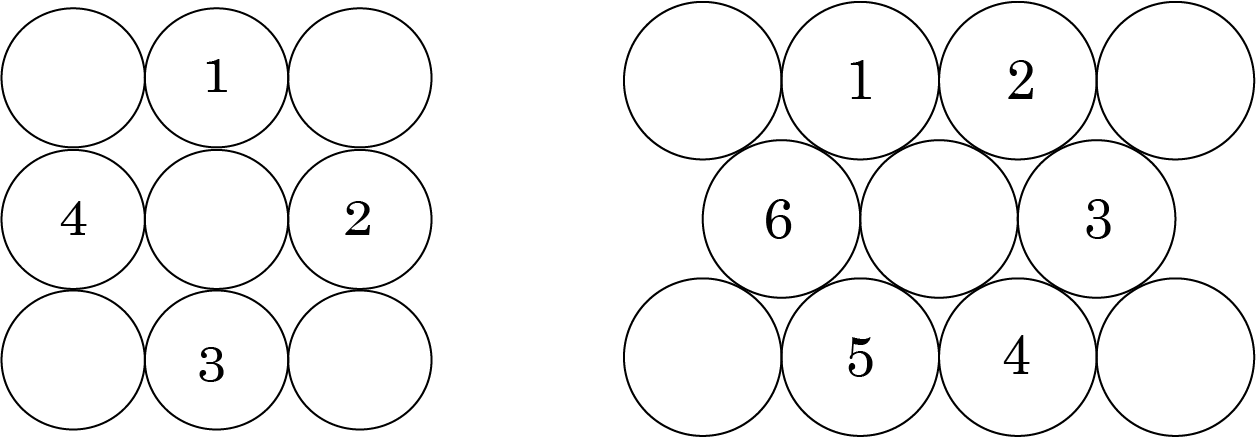
Square Packing

It is more efficient to pack hexagonally. It has a Coordination number of 6 and has fewer voids than square packing. 

If we add another layer to the square packing, we can do the following:

• A comparable layer is placed just above the foundation layer, with the second layer's spheres appearing just above the first layer's spheres, and the layers are repeated. If the first layer is designated as A, the packing is of the type AA, and the unit cell is simple cubic.

• On the other hand, we get BCC unit cells and ABAB type of packing when spheres from the second layer are inserted in depressions from the first layer.

The following are examples of hexagonal foundation layer arrangements:

When we place the second hexagonal layer A in the depressions of the first hexagonal layer A, we get two sorts of voids. Hollow and through voids of layer A and layer B are the X kind of voids. Layer B voids that are directly above spheres in layer A are referred to as Y-type voids. When the spheres of the second layer are placed over Y voids, layer 1 is repeated, and ABABAB type packing is obtained. The hexagonal unit cell is obtained in this arrangement, and the packing is known as hexagonal close packing (HCP). This packing has a 74 percent efficiency.

When the third layer is applied to X-type voids, a new layer C is created, and the process is repeated. Packing of the ABCABCABC type will be obtained. The FCC unit cell is used in this design, and the packing efficiency is 74%.

Packing of Layer B on Layer A

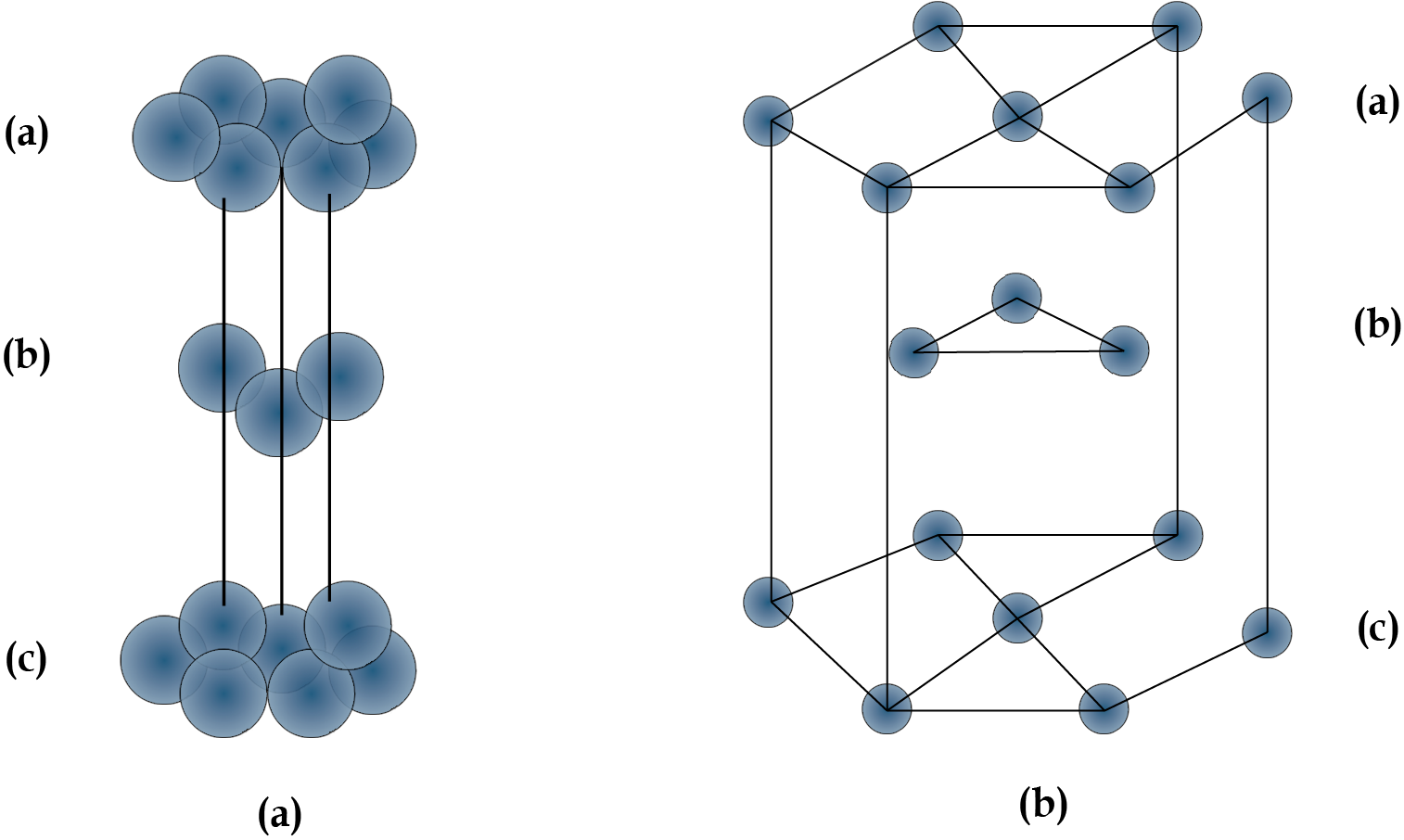
ABABA

VOIDS

Definition

Voids are the empty spaces inside a sphere. The amount and shape of voids is determined by the unit cell and packing used.

Radius Ratio

The radius ratio of a sphere that can be perfectly fit in the void to the radius of surrounding spheres is used to determine the size of the void. This is written as:

Radius ratio = \[\dfrac{{\text{r}}}{{\text{R}}}\] 

Types of voids

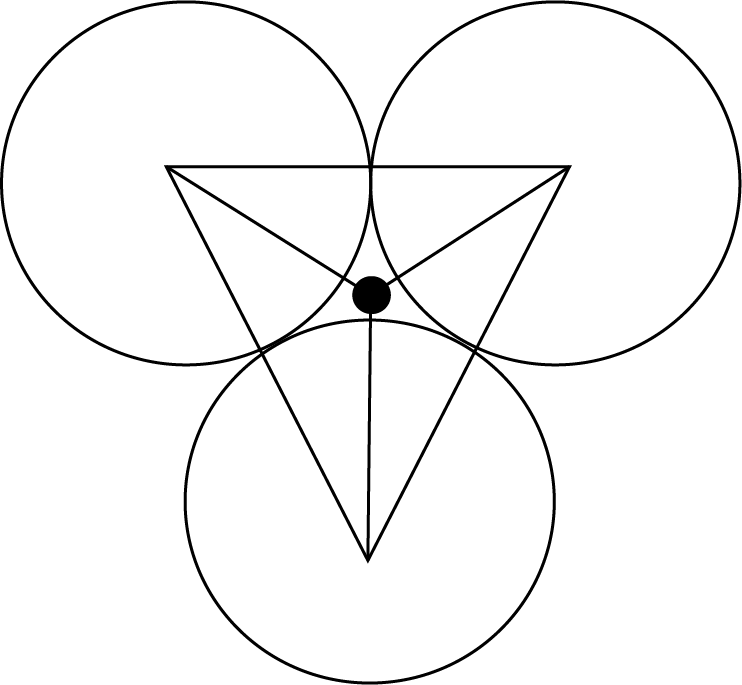
Trigonal Void

It is the void formed of equal radii which touch each other as shown in the figure.

Figure	Key Points
	Radius Ratio $\dfrac{{\text{r}}}{{\text{R}}} = 0.155$  Smallest void Coordination number is 3.

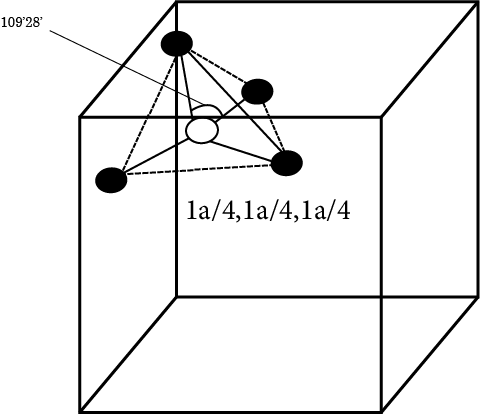
Tetrahedral Void

It is formed by the contact of four spheres and is located in the centre of a tetrahedron formed by the contact of four spheres.

Figure	Key Points
	Radius ratio $\dfrac{{\text{r}}}{{\text{R}}} = 0.225$  Number of voids in FCC crystals is 8. Position at a distance: $\dfrac{{{\text{a}}\sqrt {\text{3}} }}{{\text{4}}}$ from every corner. Coordination number is 4.

Octahedral Void:

Figure	Key Points
	Radius ratio $\dfrac{{\text{r}}}{{\text{R}}} = 0.414$  Number of voids in FCC crystals is 4. Positions: Body centre and edge centre. Rank is 4. Coordination number is 6.

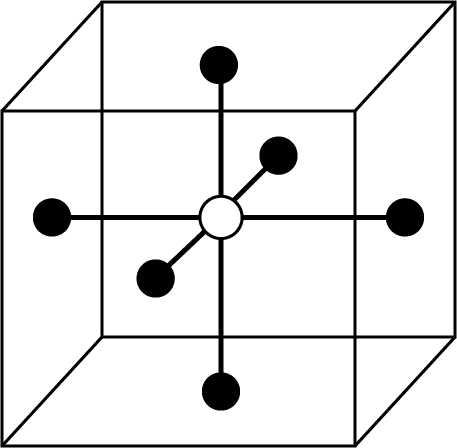
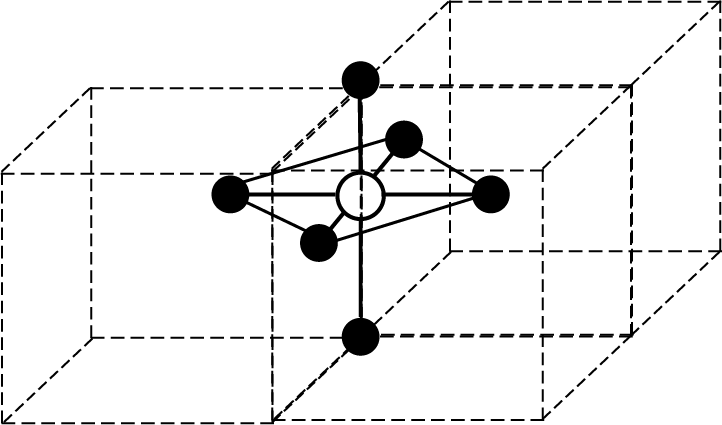
Cubic Void

The voids are formed by the close contact of eight spheres.

The following are the key points:

• Radius ratio is equal to $\dfrac{{\text{r}}}{{\text{R}}} = 0.732$ 

• Number of voids in a cubic crystal is 1.

• Position is at the body centre.

• Coordination number is 8.

• Rank 1.

It is clear from the above details that:

Trigonal < Tetrahedral < Octahedral < Cubic

Imperfections in Solid:

In a crystal structure sometimes some imperfections or defects occur:

Classification of Defects

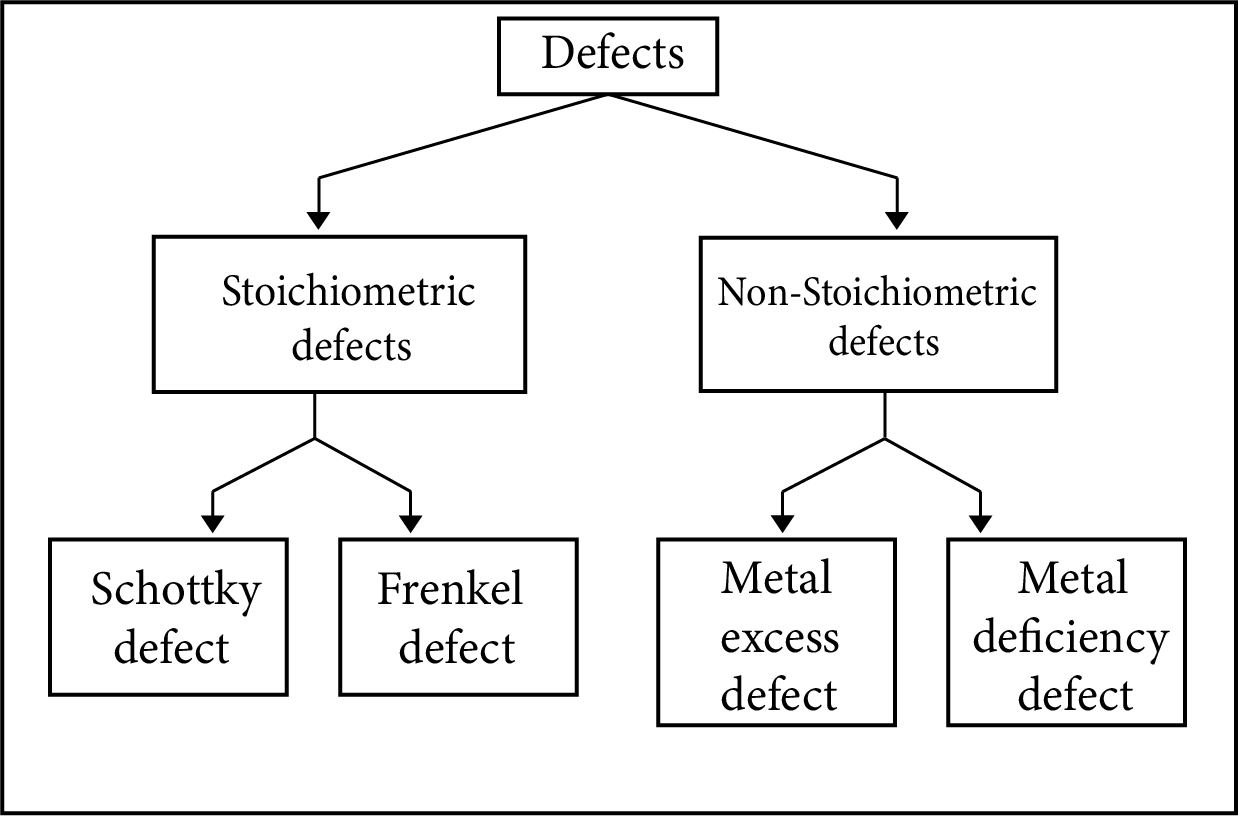
Classification of Defects

Vacancies

This type of defect occurs when the positions that should contain atoms or ions are vacant.

Interstitial Sites

These are sites located between regular positions; sometimes atoms or ions may occupy these positions.

Interstitial Sites

Stoichiometric Defects

The stoichiometry of solids are not disturbed by these defects.

Schottky Defects

In ionic solids, it's a vacancy defect. Electrical neutrality is maintained because the number of missing cations and anions is equal. The density of the substance is reduced as a result of this flaw. Ionic compounds with almost identical cation and anion sizes demonstrate the flaw. Examples are: ${\text{KCl, NaCl, AgBr}}$ etc.

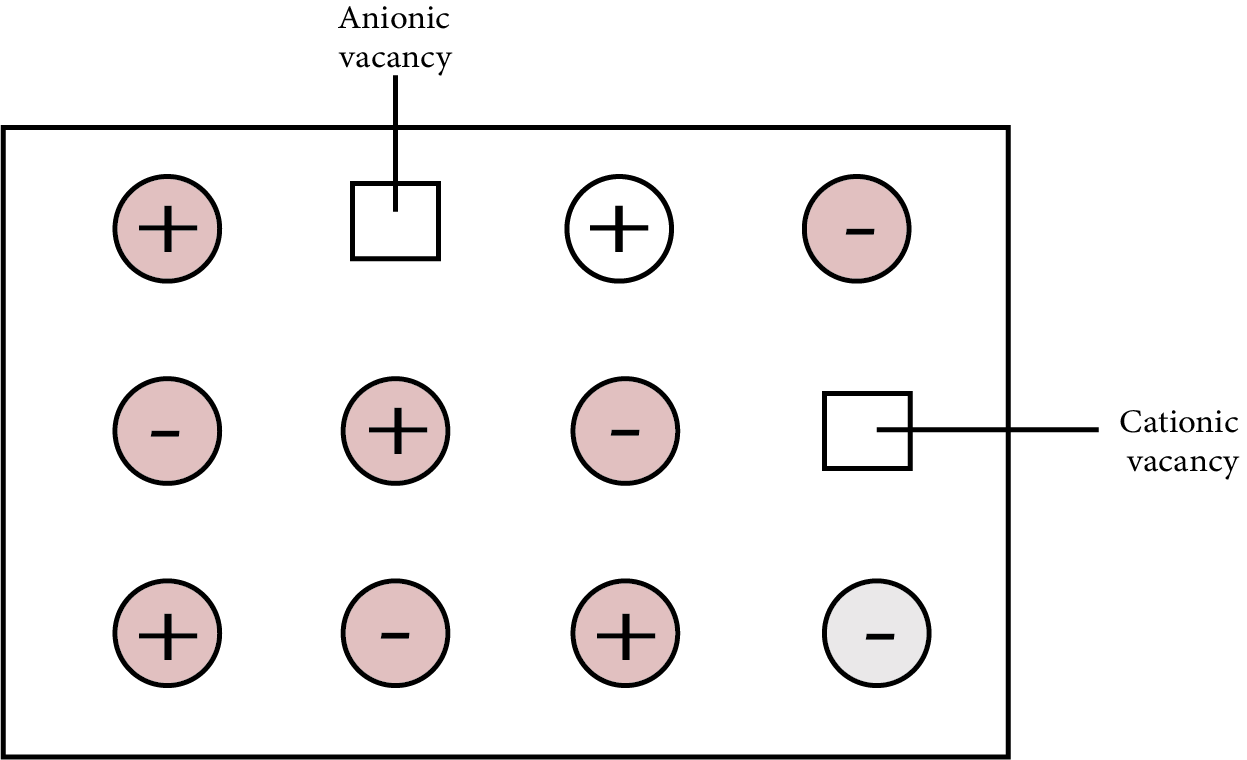
Schottky Defects

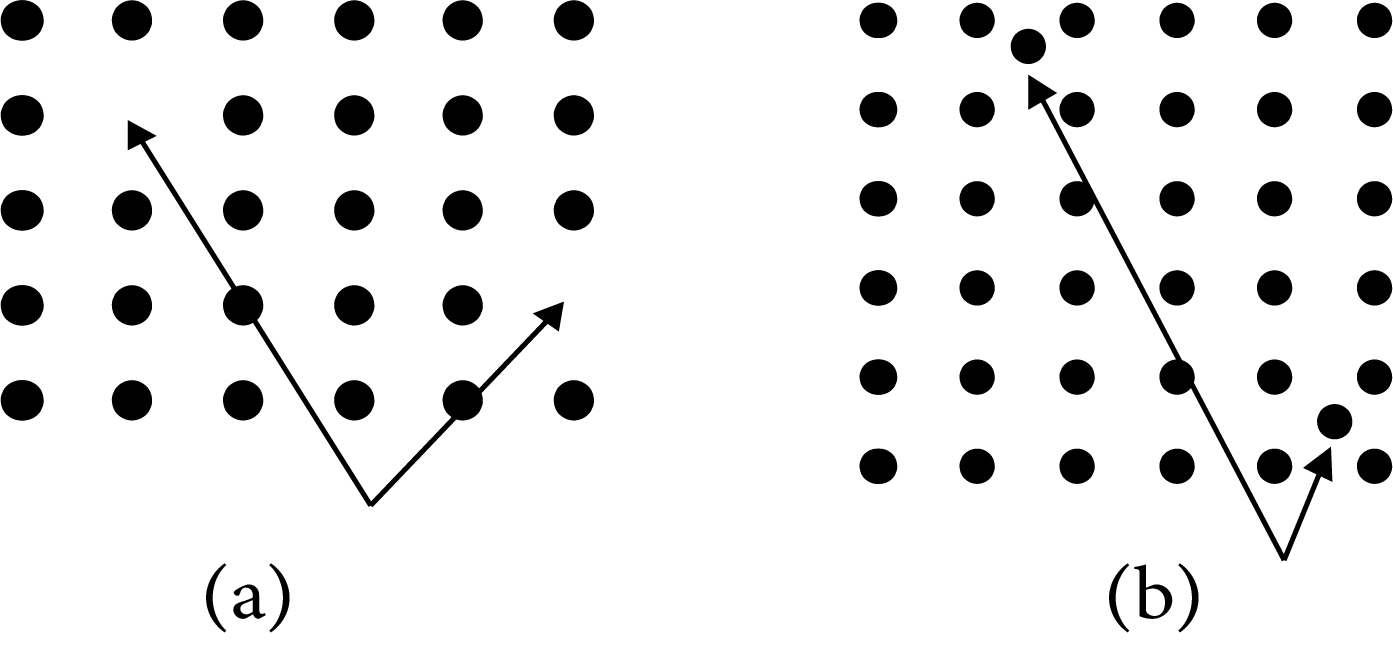
Frenkel Defect

The smaller ion is relocated from its typical position to an interstitial region in ionic solids. At its original place, it causes a vacancy defect, and at new locations, it causes an interstitial defect. Dislocation defect is another name for it. It has no effect on the solid's density. Ionic compounds with a considerable disparity in ion size are examples of this type of defect.

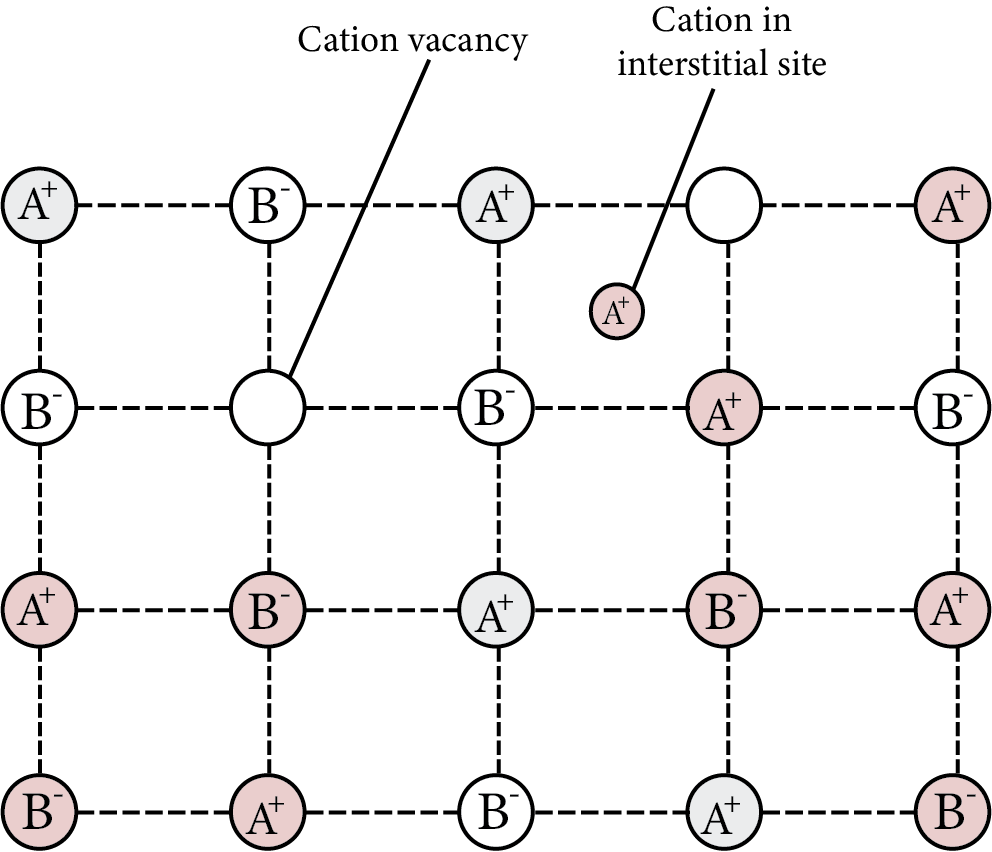
Frenkel Defect

Note: Silver bromide ${\text{(AgBr)}}$ shows Schottky and Frenkel defects both.

Non-Stoichiometric Defects

The compounds with these flaws have combined components in a different ratio than their stoichiometric formulas require.

Metal Excess Defect

Due to anionic vacancies: It's possible that the anion is absent from its lattice position, leaving an electron behind to keep the charge-balanced. The F centre is the electron-containing site. They provide the crystal colour; F stands for Farbenzenter, which means colour. This defect looks like Schottky defect and can be seen in crystals with Schottky defect. Examples: ${\text{NaCl, KCl}}$ etc.

F in a Crystal

Due to the presence of extra cations in the interstitial sites.

To maintain electrical neutrality, an additional cation may be present in one interstitial site while an electron is present in another interstitial site. This is a flaw that is similar to the Frenkel defect and can be discovered in crystals with the Frenkel defect.

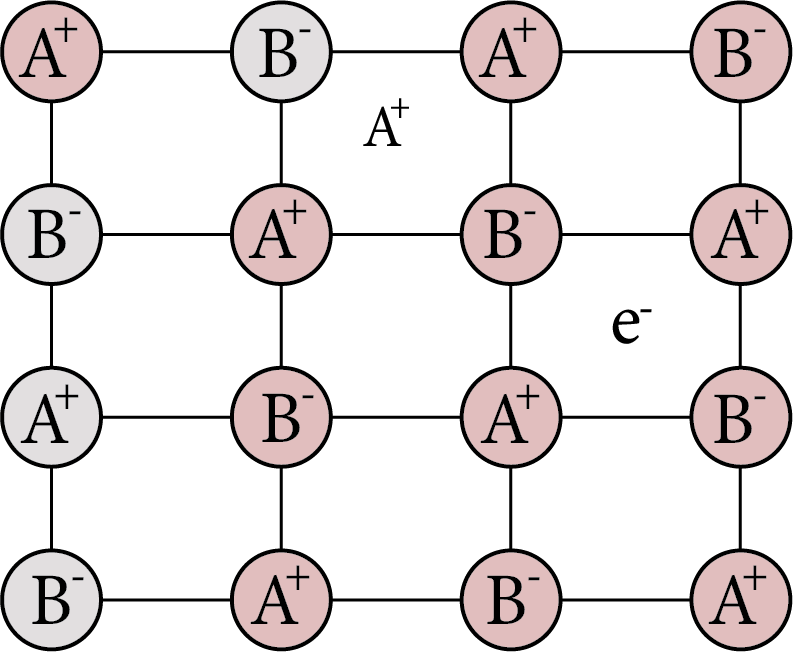
Metal  Excess Defect Cation

Metal Deficiency Defect

When metal has a fluctuating valency, this is a defect. ${\text{FeO}}$ , for example, is generally found in compositions ranging from ${\text{F}}{{\text{e}}_{{\text{0}}{\text{.93}}}}{\text{O}}$  to ${\text{F}}{{\text{e}}_{{\text{0}}{\text{.96}}}}{\text{O}}$ . Some ${\text{F}}{{\text{e}}^{{\text{ + 2}}}}$  cations are missing from ${\text{FeO}}$  crystals, but the loss of positive charge is compensated for by the existence of the requisite amount of ${\text{F}}{{\text{e}}^{{\text{ + 3}}}}$  ions.

Importance of Chemistry Class 12 Chapter Solid State

Like other states of matter, solids are also made of particles. These particles are heavily packed due to the higher intermolecular force of attraction. Due to this strong bond between the molecules, solids have a particular shape and are incapable of taking the shape of containers where they are kept.

Proceeding further, students will study that solids have higher densities than gases and liquids. It means that they pack more molecules in unit volume and show a lower rate of compressibility. They also have a definite shape and volume.

According to the Solid State NEET notes, they are classified into various types based on the bonds existing between the building blocks. These building blocks are formed due to a characteristic arrangement of molecules.

The building blocks are also called crystal lattices. Amorphous solids do not have a proper building block shape. Crystalline solids display characteristic building blocks with a particular shape. This chapter, on proceeding further, will explain how these block shapes or lattice structures differ based on the arrangement of molecules. This chapter will explain how amorphous solids differ from crystalline ones in terms of physical and chemical properties.

Based on the chemical bonding of the unit blocks, solids are also classified into polar, non-polar, hydrogen-bonded, metallic, ionic, and covalently bonded solids. On progressing further, we will also learn how the lattice structure of solids varies based on the shapes of building pieces.

To make this chapter easier to study, we have provided these revision notes prepared by our NEET experts.

Benefits of Solid State Notes for NEET PDF

• These revision notes are concise and organized in format. Our experts have covered all important topics while making precise notes for this chapter. They have prepared these notes to save your time, so you can prepare for the exams more efficiently.

• These notes will become very useful when you complete preparing this chapter and revise it before the exam. Reduce your preparation time by revising what you have studied in this chapter with these Solid State notes.

• Go through the fundamental concepts of the solid state with these notes, which will help you to answer questions in the competitive exams much faster and more accurately.

Download Solid State Class 12 Notes PDF

Now that you have understood the importance of this chapter, avail of the Solid State Class 12 notes PDF download option on Vedantu for your exam preparation. You can download this PDF for free from Vedantu. You can easily refer to these notes at your convenience during your study sessions, resolve all your doubts and learn from the techniques of answering the sample questions as implemented by the experts.

NEET Chemistry Revision Notes - Chapter Pages

Other Important Links Related to NEET Solid State