




What Are the Main Types of Optics and How Are They Used?
Optics is a branch of physics concerned with the study of light, its propagation, and the phenomena arising from its interaction with different materials. This topic encompasses the behavior of light through reflection, refraction, dispersion, interference, diffraction, and polarization. Optics also provides the foundation for understanding the functioning of various optical instruments, which are essential for scientific and technological applications.
Nature and Propagation of Light
Light is an electromagnetic wave that travels in straight lines in a homogenous medium. It can exhibit both particle and wave characteristics, but in optics, wave and ray models are primarily used to analyze different phenomena. The speed of light in vacuum is denoted as $c = 3 \times 10^8$ m/s.
Ray Optics: Reflection and Refraction
Ray optics, or geometrical optics, studies the propagation of light in terms of rays. The primary laws for this model are the laws of reflection and refraction. The law of reflection states that the angle of incidence equals the angle of reflection.
According to Snell's Law, the relationship between incident and refracted rays at the interface of two media is given by
$\dfrac{\mu_2}{\mu_1} = \dfrac{\sin i}{\sin r}$
where $\mu_1$ and $\mu_2$ are refractive indices of the respective media, $i$ is the angle of incidence, and $r$ is the angle of refraction.
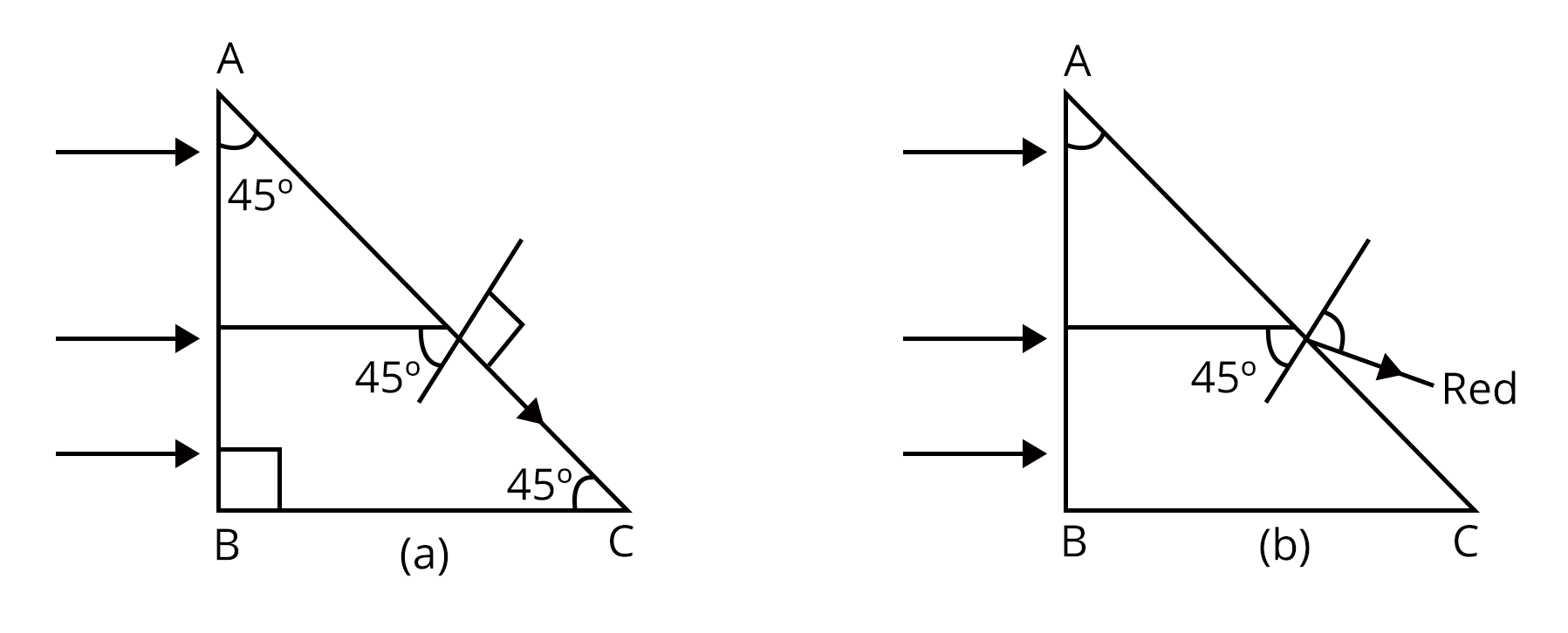
Total internal reflection occurs when a ray of light passes from a denser to a rarer medium, provided the angle of incidence exceeds the critical angle. This is mathematically represented as $\mu = \dfrac{1}{\sin C}$, where $C$ is the critical angle. Additional details are available in the section on Refraction of Light Through a Glass Slab.
Spherical Mirrors and Lenses
Spherical mirrors and lenses form images by reflecting or refracting light. The relationship between object distance ($u$), image distance ($v$), and focal length ($f$) for spherical mirrors is given by the mirror formula:
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Magnification ($m$) for mirrors is expressed as $m = -\dfrac{v}{u}$.
Lenses have two refracting surfaces and are classified as convex (converging) or concave (diverging). The lens maker's formula relates focal length to refractive index and radii of curvature:
$\dfrac{1}{f} = (\mu - 1)\left(\dfrac{1}{R_1} - \dfrac{1}{R_2}\right)$
For more about focal lengths and construction, see Sign Convention in Lenses.
Combination of Thin Lenses in Contact
When multiple thin lenses are in contact, their combined focal length ($F$) is given by
$\dfrac{1}{F} = \dfrac{1}{f_1} + \dfrac{1}{f_2} - \dfrac{d}{f_1 f_2}$
The total power of the combination equals the algebraic sum of individual powers. More information is provided at Combination of Thin Lenses in Contact.
Dispersion of Light and Prisms
Dispersion is the phenomenon where white light splits into its constituent colors when passing through a prism. The deviation angle depends on the wavelength due to material dispersion. The refractive index of a prism is:
$\mu = \dfrac{\sin\left(\dfrac{A + \delta_m}{2}\right)}{\sin (A/2)}$
where $A$ is the prism's angle and $\delta_m$ is the minimum deviation angle. The dispersive power of a prism is defined as $\omega = \dfrac{d\mu}{\mu - 1}$, where $d\mu$ is the difference in refractive indices for two wavelengths.
Explore advanced scenarios in Refraction of Light Through Prism.
Optical Instruments
Optical instruments use lenses and mirrors to form magnified or diminished images. A simple microscope uses a single lens, while compound microscopes and telescopes use multiple lenses.
The magnifying power of a simple microscope is $m = 1 + \dfrac{d}{f}$, where $d$ is the least distance of distinct vision. A compound microscope's magnification is $m = \dfrac{L}{|f_o|}\left(1 + \dfrac{d}{f_e}\right)$. For astronomical telescopes, $m = \dfrac{f_o}{-f_e}$, where $f_o$ and $f_e$ are focal lengths of objective and eyepiece, respectively.
Reflecting telescopes use mirrors and have magnification $m = \dfrac{R/2}{f_e}$, with $R$ as the mirror's radius of curvature.
Wave Optics: Interference, Diffraction, and Polarization
Wave optics analyzes light as a wave, considering phenomena like interference and diffraction. Interference occurs when waves from coherent sources superpose to form regions of constructive and destructive interference.
For two slits separated by distance $d$, the fringe width is $\beta = \dfrac{\lambda D}{d}$, with $D$ as the screen distance. Constructive and destructive interference conditions are provided by path differences of $n\lambda$ and $(2n-1)\dfrac{\lambda}{2}$, respectively.
Diffraction results in the bending of light around edges, producing patterns of maxima and minima. The single-slit minima occur at $\sin \theta_n = \dfrac{n\lambda}{a}$, where $a$ is slit width. The width of the central maximum is given by $W = \dfrac{2\lambda L}{w}$, with $L$ as screen distance and $w$ as slit width.
Polarization restricts the vibration of the electric field of light to a single plane. Brewster’s law states the tangent of the Brewster angle is the ratio of refractive indices:
$\tan \theta_B = \dfrac{n_2}{n_1}$
The law of Malus quantifies the intensity of completely polarized light after passing through an analyzer: $I \propto \cos^2\theta$.
Summary of Important Optics Formulae
| Concept | Key Formula |
|---|---|
| Mirror formula | $\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$ |
| Magnification (mirror) | $m=-\dfrac{v}{u}$ |
| Snell’s Law | $\dfrac{\mu_2}{\mu_1} = \dfrac{\sin i}{\sin r}$ |
| Lens maker’s formula | $\dfrac{1}{f} = (\mu-1)\left(\dfrac{1}{R_1}-\dfrac{1}{R_2}\right)$ |
| Compound lenses (in contact) | $\dfrac{1}{F} = \dfrac{1}{f_1}+\dfrac{1}{f_2}-\dfrac{d}{f_1 f_2}$ |
| Fringe width (YDS experiment) | $\beta = \dfrac{\lambda D}{d}$ |
| Brewster's law | $\tan\theta_B = \dfrac{n_2}{n_1}$ |
Sample Problems in Optics
A typical problem involves finding the fringe shift in Young’s double slit experiment when a glass plate is inserted in the path of one beam. If the initial shift is $x$ for a plate with refractive index $1.3$, and the shift becomes $(5/2)x$ for another plate of the same thickness, the refractive index $\mu_2$ of the second plate is found using:
$\dfrac{(\mu_2-1)}{(\mu_1-1)} = \dfrac{5}{2}$, so $\mu_2 = \dfrac{5}{2} \times (1.3-1) + 1 = 1.75$
For more solved problems and detailed derivations, see the article on Mirror Formula and Magnification.
Applications and Study Guidance
Topics in optics form a significant portion of questions in competitive exams like JEE Main. Mastery of the concepts, formulae, and applications is essential for problem solving in physics. Further reinforcement can be achieved by referring to relevant practice resources.
For more on fundamental dimensional analysis and supporting topics in physics, refer to Principle of Homogeneity of Dimensions.
Understanding Optics: Concepts, Types, and Real-Life Uses

 Share
ShareFAQs on Understanding Optics: Concepts, Types, and Real-Life Uses
1. What is optics in physics?
Optics is the branch of physics that studies the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Key points about optics include:
- Reflection and refraction of light
- Formation of images by mirrors and lenses
- Optical instruments like microscopes and telescopes
- Applications in everyday life, technology, and research
2. What are the types of optics?
Optics can be classified into two main types: geometrical optics and physical optics. These categories help explain how light behaves in different situations:
- Geometrical optics studies light as rays and focuses on reflection, refraction, and image formation by lenses and mirrors.
- Physical optics considers the wave nature of light and explains phenomena like interference, diffraction, and polarization.
- Additionally, quantum optics explores light at the quantum (photon) level.
3. What is the law of reflection?
The law of reflection states that when light reflects off a surface, the angle of incidence equals the angle of reflection. This can be summarized as:
- Angle of incidence (i) = Angle of reflection (r)
- Both the incident ray, reflected ray, and the normal lie in the same plane
- This fundamental law is used in mirrors and optical devices
4. What is refraction of light?
Refraction of light is the bending of a ray of light as it passes from one medium to another due to a change in speed. Key points of refraction include:
- Occurs at boundaries between media (like air and water)
- Described by Snell’s Law: n₁sinθ₁ = n₂sinθ₂
- Responsible for phenomena such as the apparent bending of a stick in water
5. What is the difference between concave and convex lenses?
The main difference between concave and convex lenses is in the way they bend light rays:
- Convex lens (converging lens): Thicker at the center than the edges; converges parallel rays to a focus.
- Concave lens (diverging lens): Thinner at the center than the edges; diverges parallel rays away from a focus.
- Used in spectacles, cameras, microscopes, and telescopes based on their properties.
6. What are the real and virtual images in optics?
In optics, real images are formed when light rays actually converge at a point, while virtual images are formed when rays only appear to meet when extended backward. The differences include:
- Real image: Formed on a screen, inverted, produced by convex lenses or concave mirrors
- Virtual image: Cannot be formed on a screen, upright, produced by plane mirrors or convex mirrors
7. What is total internal reflection and where is it used?
Total internal reflection (TIR) is the phenomenon where a light ray traveling from a denser medium to a rarer medium is completely reflected back at the boundary, instead of refracting. It occurs when the angle of incidence exceeds the critical angle. Key applications include:
- Optical fibers in telecommunications
- Prism-based binoculars
- Diamond sparkle due to high refractive index
8. What are the uses of convex and concave mirrors?
Convex and concave mirrors are used differently based on their image-forming properties:
- Concave mirrors: Used in shaving mirrors, headlights, dental and makeup mirrors (they can form magnified images)
- Convex mirrors: Used as rear-view mirrors in vehicles, security mirrors (they give a wider field of view)
9. State Snell’s law and its significance in optics.
Snell’s Law relates the angles and refractive indices of two media when light passes from one into another. It is expressed as:
- n₁sinθ₁ = n₂sinθ₂
- n₁ = refractive index of the first medium, n₂ = refractive index of the second medium
- The law explains refraction and is essential for lens/mirror design
10. What are the applications of optics in daily life?
Optics plays an important role in daily life and technology by enabling devices and solutions like:
- Glasses and contact lenses for vision correction
- Cameras and smartphones for capturing images
- Projectors, microscopes, and telescopes for magnification and exploration
- Optical fibers for high-speed Internet
11. What is the principle behind the working of a microscope?
The working of a microscope is based on the principles of magnification and refraction using lenses. Key points about microscope operation include:
- It uses at least two lenses: objective and eyepiece
- The objective forms a magnified real image, and the eyepiece further magnifies this image
- Light is refracted through both lenses to make small objects appear larger
12. How does the human eye function as an optical instrument?
The human eye acts as a natural optical instrument by focusing light to form real, inverted images on the retina. The process involves:
- Cornea and lens bend (refract) light
- The iris controls the amount of incoming light
- The retina detects the image and sends signals to the brain




















 Watch Video
Watch Video


