An Overview of the Velocity-Time Graph
The velocity of a moving object is defined as the rate of change of displacement of the moving object. Therefore, velocity is a vector quantity and its variation with time in graphical terms is known as the velocity-time graph or velocity-time relation. The sprinter's changing speed, as well as the speed of any other moving object or person, is displayed on a velocity-time graph. The slope of the graph line on a velocity-time graph is used to illustrate acceleration.
Velocity-Time Graph for Uniform Motion (No Acceleration)
In this case, the velocity of a moving object is constant and does not change with time, since there is no acceleration applied on the object. Therefore, for this case, one can see (as shown below in Figure (a)) that the velocity will remain constant during the whole trip despite the change in the time.
Velocity-Time Graph with a Constant Uniform Acceleration
In this case, the object is under a constant uniform acceleration, and therefore, its velocity will constantly increase or decrease depending on the applied uniform application, which is called the accelerating and retarding acceleration, respectively. In the velocity-time graph (as shown below in Figure (b)), the velocity of the object increases linearly on the application of constant uniform acceleration, and therefore, we observe a linear behaviour of the object’s velocity with time. The slope of this graph can be utilised to estimate the acceleration applied on the object.
Under a uniform constant acceleration, the equations of motion of the object can be expressed as follows:
\[v = u + at - - - - - (1)\]
\[S = ut + \dfrac{1}{2}a{t^2} - - - - - (2)\]
\[{v^2} = {u^2} - 2as - - - - - (3)\]
where u, v, a, s and t are the initial velocity, final velocity, uniform acceleration, total displacement of the object and travel/trip time, respectively.
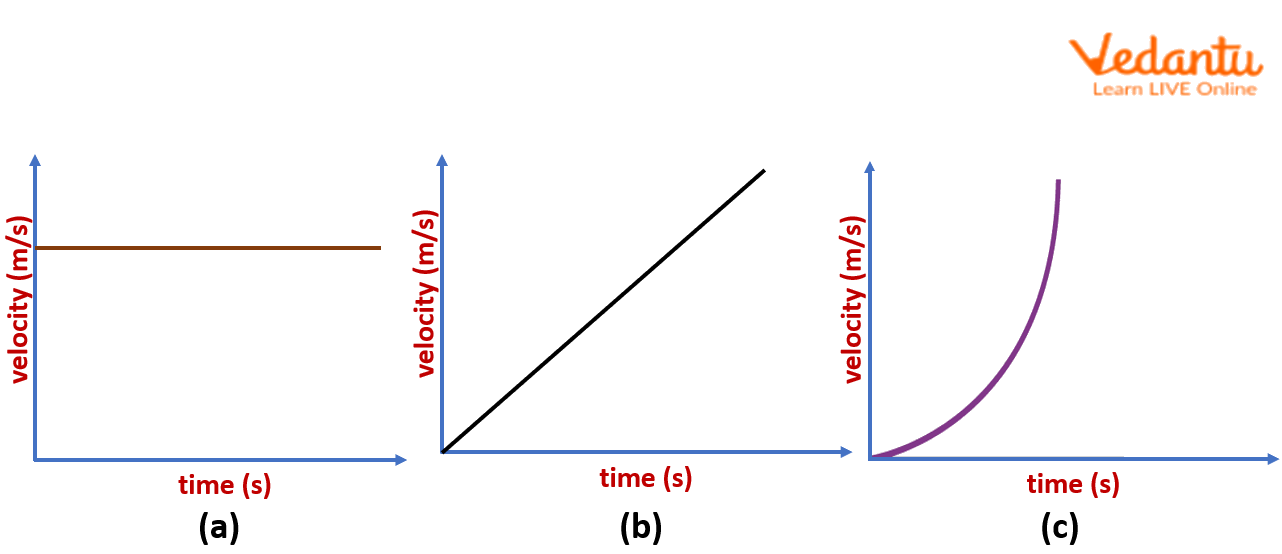
Velocity Time Graph for (a) Constant Uniform Velocity, (b) Constant Uniform Acceleration, and (c) Under a Variable Acceleration.
Velocity-Time Graph Under a Variable Acceleration
In this case, the acceleration acting on the object changes with the time, and therefore, the variation in the velocity of the object is different in the different time periods of the trip (as shown in FIgure (c) above), and therefore, we observe a velocity-time graph different from the case where the uniform acceleration is applied on the object, and we observe a parabolic behaviour of velocity with time.
Interesting Facts
Speed is a scalar quantity and velocity is a vector quantity.
The fastest speed possible is the speed of light.
In the uniform circular motion, the speed of the object remains constant while the velocity of the object varies continuously.
Key Features
Velocity is the rate of change of the displacement.
In the velocity-time graphs, the slope of the curves manifests the acceleration of the object.
The velocity of any object is based on the rate of change of displacement and therefore depends on the initial and final position of the object.
FAQs on Velocity Time Graph
1. What is the initial and final velocity?
Initial velocity of an object is the velocity of the object at t=0, i.e., when the object starts its trip and the final velocity of the object is the velocity at the end of the trip.
2. State the difference and similarity between speed and velocity.
The speed of the object is defined as the rate of change of the distance while the velocity is the rate of change of displacement of an object. Since distance and displacement are the scalar and vector quantities, respectively, therefore, speed and velocity are the scalar and vector quantities. The similarity between speed and velocity is m/s since both distance and displacement are measured in metres.
3. What are the differences between velocity and acceleration?
velocity is the rate of change of displacement while acceleration is the measure of change of velocity. Both velocity and acceleration are vector quantities. Velocity is composed of magnitude and direction. The SI unit of velocity is m/s and the SI unit of acceleration is ${m/s^2}$.
