Question

1) Discuss first minimum in Fraunhofer diffraction by single slit
2) Plot graphs of intensity for both interference and diffraction patterns. State two points of difference between these two.
3) Derive Brewster’s law for polarization.

Answer 1

Hint: 1) The relationship between slit width and the diffraction minima and diffraction maxima can be explored using the single slit calculation.
2) Interference and diffraction are phenomena that occur with waves. But diffraction occurs only for the waves which can be represented in 2D. Diffraction and interference have different intensity wave patterns.
3) By using Snell’s law we can derive the equation for Brewster’s law of polarization. Brewster’s law gives the relationship between the polarizing angle and refractive index of the medium.

Formula used:
\[\sin T=\dfrac{\lambda }{a}\]
\[\dfrac{\sin i}{\sin r}=\mu \]

Complete step by step answer:
Consider a slit of width \[a\], light wavelength \[\lambda \] and\[a<\lambda \].

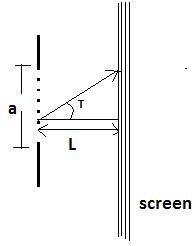
When light travels through the slit, the resulting wave pattern can be calculated by treating points in the aperture as a point source from which new waves spread out.
Let \[L\] be the distance between the slit and screen, and \[T\] be the angle between the normal line and the wave ray to a point on the screen.

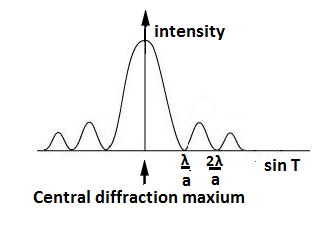
The graph shows the intensity of the light in the diffraction pattern as a function of \[\sin T\].
The light is more concentrated in the central diffraction maximum.
The first diffraction minimum occurs at the angles given by, \[\sin T=\dfrac{\lambda }{a}\]
When, \[a\sin T=\lambda \], the path difference between the top and bottom waves is zero. The path difference between top wave and bottom wave, just below the midpoint of the slit \[\left( \dfrac{a}{2} \right)\] is half of the wavelength \[\left( \dfrac{\lambda }{2} \right)\]
\[a\sin T\] is called the path difference between the two light rays. When the top parallel waves begin its cycle, the bottom waves complete two thirds of its cycle. Hence, these two light rays have path difference of about \[\dfrac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 2 }\!\!\pi\!\!\text{ or }\dfrac{\text{4 }\!\!\pi\!\!\text{ }}{\text{3}}\].
Let’s consider many point sources, say \[2k\] which are equally spaced within the slit. There are,
\[1\]to \[k\]above the midpoint and \[k+1\] to \[k+2\] below.
Considering the equation, \[a\sin T=\lambda \], waves \[1\] and \[k+1\], \[2\] and \[k+2\], \[3\] and \[k+3\]….through to \[k\] and \[2k\] are out of phase. Hence cancel each other. All the waves get cancelled and the resultant wave has an amplitude of zero. Amplitude zero indicates that zero intensity, hence the first minimum occurs at \[a\sin T=\lambda \]

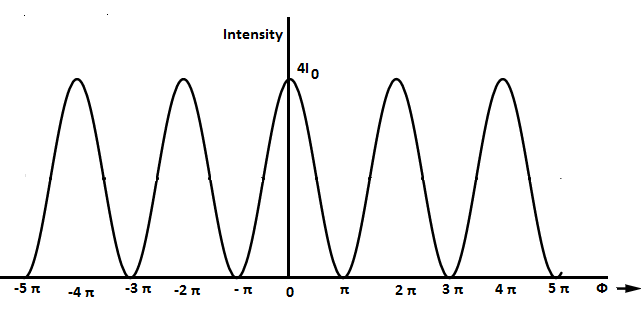
2) Intensity graph of interference

Intensity graph of diffraction

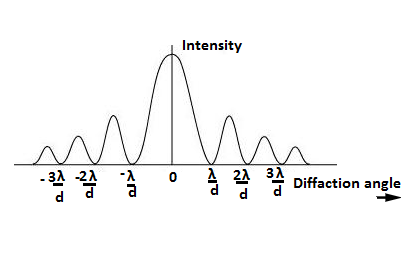
In interference, all bright fringes are of the same intensity, but for diffraction of light, all bright fringes do not have the same intensity.
Interference is the superposition of two waves starting from the two different wave fronts.
From the first figure we can see that, value of intensity remains constant throughout the fringes.
From the second figure, we can see that the intensity decreases as the order of fringes increases. The central fringes has the maximum intensity than the other fringes.

3) Brewster’s law states that, when unpolarized light rays fall on an interface, the reflected light is completely polarized, if light is incident at a polarizing angle. This angle of incidence is known as Brewster’s angle.

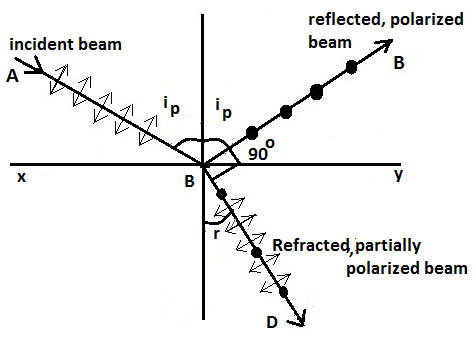
\[{{i}_{p}}+90{}^\circ +r=180{}^\circ \]
\[r=90{}^\circ -{{i}_{p}}\] ----------- 1
Where,
\[{{i}_{p}}\] is the polarizing angle
We have,
Snell’s law
\[\dfrac{\sin i}{\sin r}=\mu \] --------2
Where,
\[i\] is the angle of incidence
\[r\] is the angle of refraction
\[\mu \] is the refractive index
Then, substitute 1 in equation 2
\[\dfrac{\sin {{i}_{p}}}{\sin \left( 90{}^\circ -{{i}_{p}} \right)}=\mu \]
\[\dfrac{\sin {{i}_{p}}}{\cos {{i}_{p}}}=\mu \]
\[\mu =\tan {{i}_{p}}\]
From the above equation, Tangent of the polarizing angle is numerically equal to the refractive index of the medium.

Note:
1) Light passing through a single slit forms a diffraction pattern which is different from those formed by double slits. A single slit produces an interference pattern, which is characterized by a broad central maximum with dimmer and narrower maxima to the side.
2) Diffraction is the tendency of a wave passing through a finite aperture or emitted from a finite source or to spread out as it propagates. Diffraction results from the interference of an infinite number of waves emitted by a continuous distribution of source points.
3) Polarized sunglasses use the principle of Brewster's angle to reduce glare from the Sun. When the reflecting surface is absorbing, reflectivity at parallel polarization goes through a non-zero minimum at pseudo-Brewster's angle.