Question

1. Draw a rough sketch of a regular octagon. Draw a rectangle by joining exactly 4 of the vertices of the octagon.
2. A diagonal is a line segment that joins any two vertices of the polygon and not the side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.

Answer 1

Hint: In the first part of the question, we first have to draw a regular octagon. For that, we will first define a regular polygon. A regular polygon is a polygon with all equal sides. Hence, we will draw a regular octagon by drawing an 8 sided polygon in which all the sides are equal. Then we have to draw a rectangle by joining exactly 4 vertices of the octagon. We will do this by first choosing any two adjacent vertices and then we will select the vertices directly opposite to the pair of the adjacent vertices. Hence, we will have a rectangle. In the second part of the question, we have to draw the diagonals of a pentagon. For this, we will first draw a regular pentagon and then its diagonals as defined in the question. Thus, we will have the answer to both parts of the question.

Complete step-by-step solution:
In the first part of the question, we first need to draw a rough sketch of a regular octagon. For this, we need to know the meaning of a “regular polygon”. A regular polygon is the one in which all the sides of the polygon are equal.
Here, we have to draw a regular octagon. We know that an octagon is an 8 sided polygon and since we have to draw a regular octagon, all of its 8 sides should be equal in length.
Hence, a regular octagon is shown as follows:

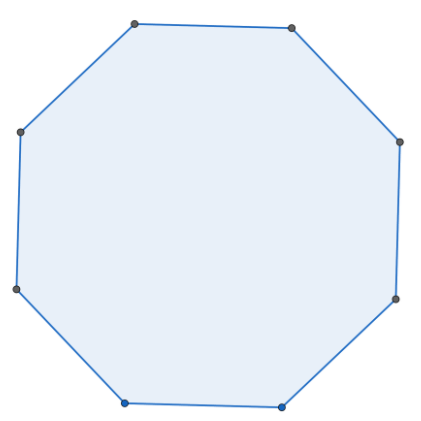
This is a regular octagon.
Now, we have to join exactly 4 of its sides to draw a rectangle in it. It is done as follows:
We will select 4 vertices such that two vertices are adjacent and the other two are opposite to the adjacent pair of the vertices. Then we will mark the rectangle as ABCD. Thus, we get our rectangle ABCD inside the octagon as:

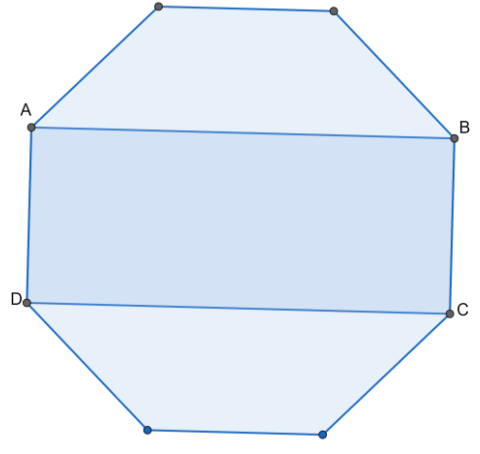
Hence, we get both our regular octagon and a rectangle formed by joining 4 of its vertices.
In the second part of the question, we have to draw a pentagon and its diagonals.
We know that pentagon is a 5 sided polygon and the definition of a diagonal is already mentioned in the question.
We here can take any kind of pentagon but for the sake of convenience, we will draw a regular pentagon.
A regular polygon is given as follows:

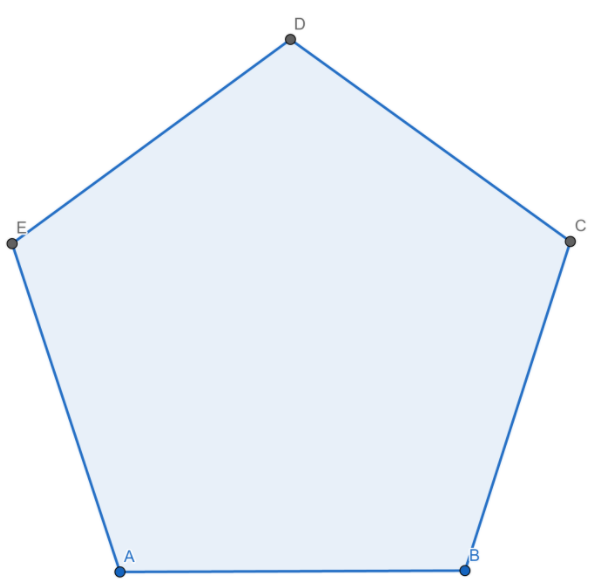
Now, we will draw its diagonals. For that, we will join all the vertices with every other vertex except for the adjacent vertices as they will form the side of the pentagon.
Hence, we get the diagonals of the pentagon as:

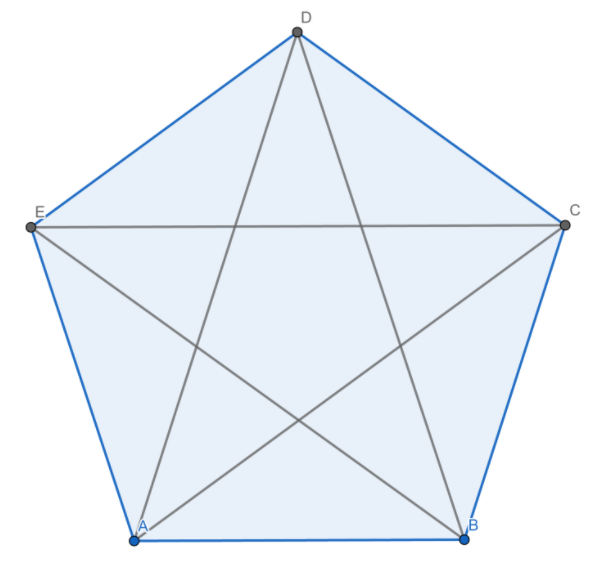
Thus, the diagonals of the pentagon ABCD are AC, AD, BD, BE, and CE.

Note: Always remember that in a regular polygon, not only the sides but also the measure of all the interior angles is also the same. Thus, all the interior angles will be equal in the regular octagon and the regular pentagon that we drew here. Also, the measure of each angle in a regular ‘n’ sided polygon is given by the formula:
$\left( \dfrac{n-2}{n} \right){{180}^{\circ }}$