Question

(5, -10), (-15, 15) and (5, 5) are the coordinates of vertices A, B and C respectively of the triangle ABC and P is a point on median AD such that AP: PD = 2:3. Ratio of the areas of the triangle PBC and ABC is?
(a) 2:3
(b) 3:4
(c) 3:5
(d) 4:5

Answer 1

Hint: Draw a rough diagram of the triangle ABC with the given coordinates and the median AD. Assume the coordinates of A, B and C as $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ respectively. Now, find the coordinates of the point D by using the midpoint formula given as ${{x}_{D}}=\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2} \right)$ and ${{y}_{D}}=\left( \dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$. Now, consider the ratio 2:3 = m: n and find the coordinates of the point P on the median AD. Use the section formula ${{x}_{P}}=\left( \dfrac{m{{x}_{D}}+n{{x}_{1}}}{m+n} \right)$ and ${{y}_{P}}=\left( \dfrac{m{{y}_{D}}+n{{y}_{1}}}{m+n} \right)$. Find the area of the triangles ABC and PBC using the formulas \[\dfrac{1}{2}\left| \left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right] \right|\] and \[\dfrac{1}{2}\left| \left[ {{x}_{P}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{P}} \right)+{{x}_{3}}\left( {{y}_{P}}-{{y}_{2}} \right) \right] \right|\] respectively. Take the ratio of area of the triangle PBC and ABC to get the answer. If the area turns out to be negative then take its absolute value.

Complete step by step answer:
Here we have been provided with the coordinates of the vertices A, B and C of a triangle and we are asked to find the ratio of the area of the triangles PBC and ABC when AD is a median and P is a point dividing the median in a certain ratio.

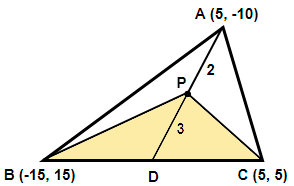
Now, in the above diagram we have considered the coordinates of A, B and C as $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ respectively. The coordinates of D and P are assumed as $\left( {{x}_{D}},{{y}_{D}} \right)$ and $\left( {{x}_{P}},{{y}_{P}} \right)$ respectively. So we have the values $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 5,-10 \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)=\left( -15,15 \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)=\left( 5,5 \right)$.
(i) Since AD is the median of the triangle therefore it bisects the side BC of the triangle so using the midpoint formula we get,
For the x – coordinate,
$\begin{align}
  & \Rightarrow {{x}_{D}}=\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2} \right) \\
 & \Rightarrow {{x}_{D}}=\left( \dfrac{-15+5}{2} \right) \\
 & \Rightarrow {{x}_{D}}=-5 \\
\end{align}$
For the y – coordinate,
$\begin{align}
  & \Rightarrow {{y}_{D}}=\left( \dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right) \\
 & \Rightarrow {{y}_{D}}=\left( \dfrac{15+5}{2} \right) \\
 & \Rightarrow {{y}_{D}}=10 \\
\end{align}$
Therefore the coordinates of D is $\left( -5,10 \right)$.
(ii) Since the point P is present on the median AD such that AP: PD = 2:3, so assuming this ratio as m: n and applying the section formula we get,
For the x coordinate,
$\begin{align}
  & \Rightarrow {{x}_{P}}=\left( \dfrac{2\times \left( -5 \right)+3\times \left( 5 \right)}{2+3} \right) \\
 & \Rightarrow {{x}_{P}}=\left( \dfrac{-10+15}{5} \right) \\
 & \Rightarrow {{x}_{P}}=1 \\
\end{align}$
For the y coordinate,
$\begin{align}
  & \Rightarrow {{y}_{P}}=\left( \dfrac{2\times \left( 10 \right)+3\times \left( -10 \right)}{2+3} \right) \\
 & \Rightarrow {{y}_{P}}=\left( \dfrac{20-30}{5} \right) \\
 & \Rightarrow {{y}_{P}}=-2 \\
\end{align}$
Therefore the coordinates of P is $\left( 1,-2 \right)$.
We know that the area of a triangle with coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is given by the relation \[\dfrac{1}{2}\left| \left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right] \right|\], so we have,
$\Rightarrow $ Area of the triangle ABC = \[\dfrac{1}{2}\left| \left[ 5\left( 15-5 \right)+\left( -15 \right)\left( 5-\left( -10 \right) \right)+5\left( -10-15 \right) \right] \right|\]
$\Rightarrow $ Area of the triangle ABC = 150 square units
Similarly, we can write the area of the triangle PBC as \[\dfrac{1}{2}\left| \left[ {{x}_{P}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{P}} \right)+{{x}_{3}}\left( {{y}_{P}}-{{y}_{2}} \right) \right] \right|\], so we have,
$\Rightarrow $ Area of the triangle ABC = \[\dfrac{1}{2}\left| \left[ 1\left( 15-5 \right)+\left( -15 \right)\left( 5-\left( -2 \right) \right)+5\left( -2-15 \right) \right] \right|\]
$\Rightarrow $ Area of the triangle ABC = 90 square units
Taking the ratio of areas of the triangles PBC and ABC we get,
$\begin{align}
  & \Rightarrow \dfrac{Ar.\left( PBC \right)}{Ar.\left( ABC \right)}=\dfrac{90}{150} \\
 & \therefore \dfrac{Ar.\left( PBC \right)}{Ar.\left( ABC \right)}=\dfrac{3}{5} \\
\end{align}$

So, the correct answer is “Option c”.

Note: Here we do not have to apply the Heron’s formula to calculate the area of the triangle as it would require much calculation while finding the length of each side using the distance formula. Also the formula of the area of the triangle given as $\dfrac{1}{2}\times $ base $\times $ height would be suggested not to apply as in this case we need to find the coordinates of the foot of the perpendicular from A and P to the side BC.