
5 questions are asked in a question paper out of which two questions can be solved with two-two methods, two questions can be solved with three-three methods and one question can be solved by only one method then the number of possible attempts to solve the question paper are?
A. ${2^2}$
B. ${2^2} \cdot {3^2} \cdot {1^2}$
C. 144
D. 288
Answer
555.3k+ views
Hint: The number of possible attempts here means the number of ways in which the paper can be solved. As such, find the number of possible methods in which each question can be solved and then multiply the same to get every permutation and combination possible.
Complete step by step solution:
In this question, first let us take 5 alphabets which will represent our five questions asked in the question paper. So, we name them A, B, C, D and E.
Say A and B are the questions which can be solved by two methods each.
C and D are the ones which have solutions laid to 3 methods each.
Finally, there is E which has only one method to solve the question.
Thus, we can write the same as this.
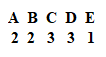
Now multiplying the numbers written below, we get the result which is ${2^2} \cdot {3^2} \cdot 1$ which when observing the options relates to option ‘b’ as ${1^2} = 1$.
As such from the options, the number of attempts that can be done is ${2^2} \cdot {3^2} \cdot {1^2}$.
Note:
Whenever solving such questions, adding the number of ways will give the wrong answer because the questions are not being attempted in any set pattern and as such the randomness of selection of question as well as the method to solve it can be dealt with by multiplication only.
Complete step by step solution:
In this question, first let us take 5 alphabets which will represent our five questions asked in the question paper. So, we name them A, B, C, D and E.
Say A and B are the questions which can be solved by two methods each.
C and D are the ones which have solutions laid to 3 methods each.
Finally, there is E which has only one method to solve the question.
Thus, we can write the same as this.
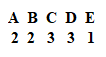
Now multiplying the numbers written below, we get the result which is ${2^2} \cdot {3^2} \cdot 1$ which when observing the options relates to option ‘b’ as ${1^2} = 1$.
As such from the options, the number of attempts that can be done is ${2^2} \cdot {3^2} \cdot {1^2}$.
Note:
Whenever solving such questions, adding the number of ways will give the wrong answer because the questions are not being attempted in any set pattern and as such the randomness of selection of question as well as the method to solve it can be dealt with by multiplication only.
Recently Updated Pages
Master Class 7 English: Engaging Questions & Answers for Success

Master Class 7 Maths: Engaging Questions & Answers for Success

Master Class 7 Science: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Trending doubts
The value of 6 more than 7 is A 1 B 1 C 13 D 13 class 7 maths CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

The plural of Chief is Chieves A True B False class 7 english CBSE

Write a letter to the editor of the national daily class 7 english CBSE





