
A 3p orbital has:
A.two non-spherical nodes
B.two spherical nodes
C.one spherical and non-spherical nodes
D.one spherical and two non-spherical nodes
Answer
221.1k+ views
Hint: Node is a point or space around the nucleus where the probability of finding an electron is zero. This point where the wave function that describes the respective orbital is zero. There are 2 types of nodes, radial nodes also called spherical nodes and angular nodes which can be called non-spherical nodes. Spherical nodes can be found out by equation \[n - 1 - 1\] and there are a number of non-spherical nodes.
Complete step by step solution:
We have to find the number of nodes present in the 3p orbital. For that we want to know the principal quantum number (n) and azimuthal quantum number (l) of 3p orbital. The table given below gives the value of n l and ml value of different orbitals,
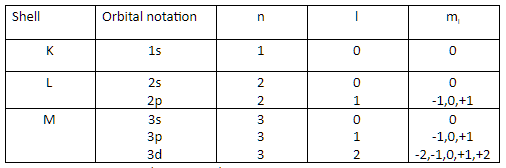
For 3p orbital we have \[n = 3,l = 1\]
Total number of nodes= \[n - 1\] , that is 3-1=2.
Number of spherical nodes= \[n - 1 - 1\] , that is 3-1-1=1
Number of non-spherical node or angular node= \[l = 1\]
There are a total of two nodes, they are one spherical node and one non-spherical node.
Hence, the answer is option (C) i.e One Spherical and non-spherical nodes.
Note: Electrons are arranged in an atom. The energy and the location of every electron in an atom is determined by a set of quantum numbers. The Principal quantum number is the shell number itself which represents the energy level. Azimuthal quantum number l is found by \[n - 1\] and the ml value varies from –l to +l. Azimuthal quantum number gives the orbital angular momentum and describes the shape of the orbital. Magnetics quantum denotes the different orientation possible for the different orbits. Those numbers describe different atomic orbits. Atomic orbital is the region of probability where the electron can be found. a spherical node can be defined as the spherical surface where the probability of finding an electron is zero. Nodes other than spherical nodes are considered as the non-spherical nodes.
Complete step by step solution:
We have to find the number of nodes present in the 3p orbital. For that we want to know the principal quantum number (n) and azimuthal quantum number (l) of 3p orbital. The table given below gives the value of n l and ml value of different orbitals,

For 3p orbital we have \[n = 3,l = 1\]
Total number of nodes= \[n - 1\] , that is 3-1=2.
Number of spherical nodes= \[n - 1 - 1\] , that is 3-1-1=1
Number of non-spherical node or angular node= \[l = 1\]
There are a total of two nodes, they are one spherical node and one non-spherical node.
Hence, the answer is option (C) i.e One Spherical and non-spherical nodes.
Note: Electrons are arranged in an atom. The energy and the location of every electron in an atom is determined by a set of quantum numbers. The Principal quantum number is the shell number itself which represents the energy level. Azimuthal quantum number l is found by \[n - 1\] and the ml value varies from –l to +l. Azimuthal quantum number gives the orbital angular momentum and describes the shape of the orbital. Magnetics quantum denotes the different orientation possible for the different orbits. Those numbers describe different atomic orbits. Atomic orbital is the region of probability where the electron can be found. a spherical node can be defined as the spherical surface where the probability of finding an electron is zero. Nodes other than spherical nodes are considered as the non-spherical nodes.
Recently Updated Pages
The hybridization and shape of NH2 ion are a sp2 and class 11 chemistry JEE_Main

What is the pH of 001 M solution of HCl a 1 b 10 c class 11 chemistry JEE_Main

Aromatization of nhexane gives A Benzene B Toluene class 11 chemistry JEE_Main

Show how you will synthesise i 1Phenylethanol from class 11 chemistry JEE_Main

The enolic form of acetone contains a 10sigma bonds class 11 chemistry JEE_Main

Which of the following Compounds does not exhibit tautomerism class 11 chemistry JEE_Main

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Other Pages
NCERT Solutions For Class 11 Chemistry Chapter 7 Redox Reaction

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Hydrocarbons Class 11 Chemistry Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Chemistry Chapter 5 CBSE Notes - 2025-26

NCERT Solutions ForClass 11 Chemistry Chapter Chapter 5 Thermodynamics

Equilibrium Class 11 Chemistry Chapter 6 CBSE Notes - 2025-26




