Question

A $9V$ battery with an internal resistance of $0.5\Omega $ is connected across an infinite network as shown in the figure. All ammeters ${A_1},{A_2},{A_3}$ and voltmeter $V$ are ideal. Choose the correct statement.

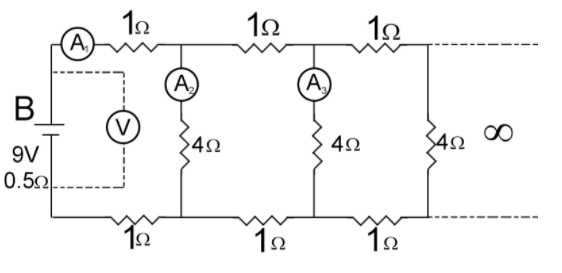
A.Reading of ${A_1}$ is \[2A\] .
B.Reading of \[V\] is \[7V\] .
C.Reading of \[V\] is \[9V\] .
D.Reading of \[{A_1}\] is \[18A\] .

Answer 1

Hint: You can start by defining ohm’s law, voltmeter and ammeter. Then draw a new diagram of the circuit and in it replace the infinite resistors with a resistor \[y\] which will be the effective resistance of the circuit. Then given that the fact some new resistors will not change the effective resistance of the circuit significantly, you can use \[1 + \dfrac{{4y}}{{4 + y}} + 1 = y\] to find the value of \[y\] . Then use the equation \[I = \dfrac{E}{{r + R}}\] to find the value of \[{A_1}\] . Then use the equation \[V = E - IR\] to find the value of \[V\] .

Complete answer:
Ohm’s law – This law defines the relationship between current and voltage. According to ohm’s law, the current flowing through a conductor is directly proportional to the voltage difference across the ends of the conductor.
\[I \propto V\]
\[I = \dfrac{V}{R}\]
Here \[I = \] current, \[V = \] Voltage, and \[R = \] resistance
Voltmeter – It is electrical equipment that is used to measure the potential difference between two points on an electrical circuit.
Ammeter - It is a piece of electrical equipment that is used to measure the circuit flowing two points on an electrical circuit or through a whole circuit.
In this system, we have an infinite network of resistors. An infinite network means that the addition of a few more resistors will not affect the effective resistance of the system significantly.
Let’s arrange the given circuit in the following form.

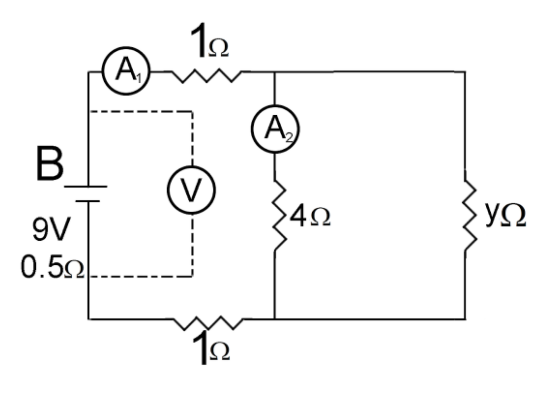
Here \[y\] is the effective resistance of the infinite system of the resistor.
The resistance of parallel resistors \[y\] and \[4\Omega \] are
\[\dfrac{{4y}}{{4 + y}}\]
So the total effective resistance of the circuit is equal to
\[1 + \dfrac{{4y}}{{4 + y}} + 1 = y\]
\[4y + 2(4 + y) = y(4 + y)\]
\[6y + 8 = 4y + {y^2}\]
\[{y^2} - 2y - 8 = 0\]
Solving this quadratic equation
\[y = \dfrac{{2 \pm \sqrt {4 + 32} }}{2}\]
\[y = \dfrac{8}{2}\]
\[y = 4\Omega \]
For the ammeter reading that measures the total current in the circuit
\[I = \] Current through \[{A_1} = \dfrac{E}{{r + R}} = \dfrac{9}{{0.5 + 4}} = 2A\]
Here, \[r = \] The internal resistance of the battery and \[R = \] effective resistance of the given circuit
For the voltmeter reading that is connected across the battery
\[V = E - IR = 9 - 2 \times 0.5\]
\[V = 8V\]

Hence, option A is the correct choice.

Note:
In the solution above we said that \[1 + \dfrac{{4y}}{{4 + y}} + 1 = y\] is equal to the effective resistance of the circuit. This can be a bit confusing, but remember \[y\] is the result of a combination of infinite resistors, so adding a few more resistors to the circuit will not make the effective resistance significantly different. In reality, the effective resistance will change but we usually ignore it for such problems.