Question

A, B and C are three points in a uniform electric field. The electric potential is:

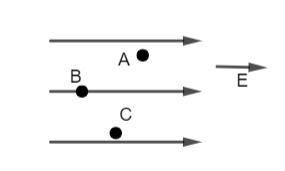
(a) Maximum at A
(b) Maximum at B
(c) Maximum at C
(d) Same at all the three points A, B and C

Answer 1

Hint: The electric field € and the potential changes with the distance of the point from the charge. The electric field at a point in the field is equal to the negative of the potential gradient. So use the concept of equipotential surface and calculate the momentum potential from points A, B and C placed in the electric field.

Complete step by step answer:

We know that the electric field intensity and the electric potential vary with the distance of the point from the charge. The relation between the electric field intensity and the potential is given as
\[E=\dfrac{-dV}{dx}.....\left( i \right)\]
This is the work done per unit charge displaced is nothing but the increase in potential dV, i.e. dV is the small change in potential over the distance dx.
The quantity from equation (i), \[\dfrac{dV}{dx}\] represents the rate of change of potential with respect to the distance in the direction of the intensity. The negative in equation (i) implies that the potential decreases with the distance measured in the direction of the electric field E.
So, according to the above concept, the potential at B must be greater but it has one condition which is described as below.
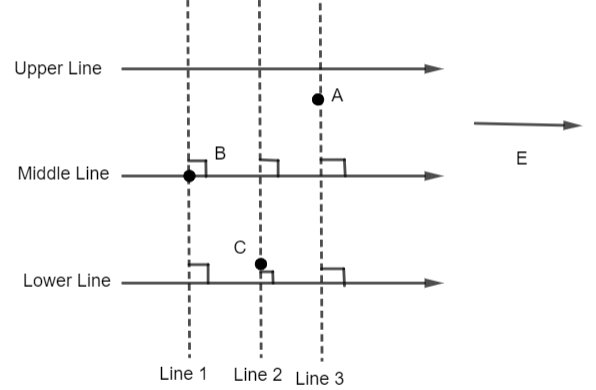
We know that the line perpendicular to the direction of \[\overrightarrow{E},\] the points on that has some potential. A line 1 is drawn from point A, then the potential on every point of line 1 will be the same including A. Similarly with line 2 and line 3. That is, these lines (line 1, line 2 and line 3) can be called an equipotential surface. In the case of an equipotential surface, the electric field at every point is always normal (to the direction of the electric field (E)).
Therefore, the potential at point B is more than C and B. So, the potential at points are \[{{V}_{B}}>{{V}_{C}}>{{V}_{A}}.\] Hence, the electric potential at point B is maximum.
Therefore, option (b) is the right answer.
Additional Information: The electric field intensity at any point in the electric field is equal to the negative rate of change of potential with respect to the distance at that particular point which is measured in the direction of electric intensity.
S.I unit of the potential gradient is volt/meter (V/m).
Since dV is the potential and work done per unit charge displaced is the increase in the potential and it is found that the work done does not depend upon the path chosen for moving the test charge from one point to the other.

Note:
The term is given in the equation (i), \[\dfrac{dV}{dx}\] is also known as a potential gradient. A surface passing through all the points at the same potential in an electric field is known as the equipotential surface. Hence, no work is done in moving a charge on the equipotential surface. The potential decreases in the direction of the electric intensity because work done is done by the field and increases in the opposite direction of E because work is done on the field.