
Answer
113.7k+ views
Hint We need to find the time taken by the ball to reach the floor for the first collision. Thereby we shall decrease the velocity of the ball and then again compute the same. We will use the formula $v = u + at$ and $S = ut + \dfrac{1}{2}a{t^2}$, where $v$ is the final velocity, $u$ is the initial velocity, $t$ is time, $a$ is the acceleration, and $S$ is the displacement.
Complete Step by step solution The time for the first collision is the time taken by the ball to drop from $90m$.
We will find that using $S = ut + \dfrac{1}{2}a{t^2}$, where the initial velocity $u$ is $0$, the acceleration is equal to the acceleration due to gravity, and $S$ is given in the question to be $90m$ .
We substitute the above values in $S = ut + \dfrac{1}{2}a{t^2}$, to get
$ \Rightarrow - 90m = (0)t + \dfrac{1}{2}( - g){t^2}$
$ \Rightarrow - 180m = ( - g){t^2}$
The value of acceleration due to gravity is $g = 9.8m/{s^2}$.
$ \Rightarrow - 180m = ( - 9.8m/{s^2}){t^2}$
$ \Rightarrow {t^2} = \dfrac{{180m}}{{9.8m/{s^2}}}$, or $t = \sqrt {\dfrac{{180}}{{9.8}}} s = \dfrac{{30}}{7}s$.
At this time, the value of $v$ can be found using $v = u + at$, where $t = \dfrac{{30}}{7}s$, and $a = - 9.8m/{s^2}$.
$ \Rightarrow v = 0 + ( - 9.8)\dfrac{{30}}{7}$, as initial velocity is $0$,
$ \Rightarrow v = - 42m/s$.
It is given that the ball loses one- tenth of its speed. Thus the speed after the first collision is ${u_1} = \dfrac{9}{{10}}(42m/s) = 37.8m/s$
Now the next collision will happen when the ball has reached the maximum height and returned to the same speed but opposite sign, just before the second collision.
The time taken for the second collision is calculated using $v = u + at$, where we substitute value to get, $( - 37.8m/s) = (37.8m/s) + ( - 9.8m/{s^2}){t_1}$
$ \Rightarrow ( - 75.6m/s) = ( - 9.8m/{s^2}){t_1}$
On further simplifying the equation we get,
$ \Rightarrow {t_1} = \dfrac{{75.6}}{{9.8}}s$
$ \Rightarrow {t_1} = \dfrac{{54}}{7}s$.
This is the time between the first and the second collisions.
Thus the total time at which the second collision occurs is
$t + {t_1} = \dfrac{{30}}{7} + \dfrac{{54}}{7} = \dfrac{{84}}{7} = 12s$
Therefore the second collision occurs at $12s$ after the ball is released from a height of $90m$.
Using these above information, we get the velocity-time graph as,
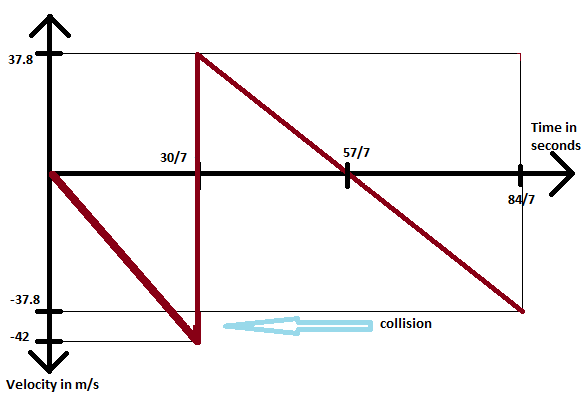
However, we require the speed- time graph and not the velocity- time graph.
Thus we will only take the absolute values of the velocities and use them for drawing the graph.
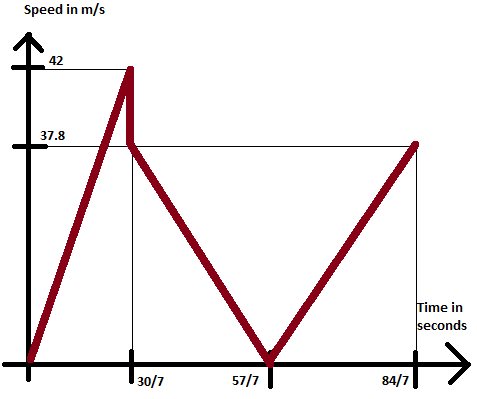
Here we have made the plot till before the second collision occurs.
Note Here we have assumed the sign convention as negative towards the earth and positive away from the acceleration due to gravity. Thus the signed value of acceleration due to gravity is $g = - 9.8m/{s^2}$ which is directed towards the earth.
Complete Step by step solution The time for the first collision is the time taken by the ball to drop from $90m$.
We will find that using $S = ut + \dfrac{1}{2}a{t^2}$, where the initial velocity $u$ is $0$, the acceleration is equal to the acceleration due to gravity, and $S$ is given in the question to be $90m$ .
We substitute the above values in $S = ut + \dfrac{1}{2}a{t^2}$, to get
$ \Rightarrow - 90m = (0)t + \dfrac{1}{2}( - g){t^2}$
$ \Rightarrow - 180m = ( - g){t^2}$
The value of acceleration due to gravity is $g = 9.8m/{s^2}$.
$ \Rightarrow - 180m = ( - 9.8m/{s^2}){t^2}$
$ \Rightarrow {t^2} = \dfrac{{180m}}{{9.8m/{s^2}}}$, or $t = \sqrt {\dfrac{{180}}{{9.8}}} s = \dfrac{{30}}{7}s$.
At this time, the value of $v$ can be found using $v = u + at$, where $t = \dfrac{{30}}{7}s$, and $a = - 9.8m/{s^2}$.
$ \Rightarrow v = 0 + ( - 9.8)\dfrac{{30}}{7}$, as initial velocity is $0$,
$ \Rightarrow v = - 42m/s$.
It is given that the ball loses one- tenth of its speed. Thus the speed after the first collision is ${u_1} = \dfrac{9}{{10}}(42m/s) = 37.8m/s$
Now the next collision will happen when the ball has reached the maximum height and returned to the same speed but opposite sign, just before the second collision.
The time taken for the second collision is calculated using $v = u + at$, where we substitute value to get, $( - 37.8m/s) = (37.8m/s) + ( - 9.8m/{s^2}){t_1}$
$ \Rightarrow ( - 75.6m/s) = ( - 9.8m/{s^2}){t_1}$
On further simplifying the equation we get,
$ \Rightarrow {t_1} = \dfrac{{75.6}}{{9.8}}s$
$ \Rightarrow {t_1} = \dfrac{{54}}{7}s$.
This is the time between the first and the second collisions.
Thus the total time at which the second collision occurs is
$t + {t_1} = \dfrac{{30}}{7} + \dfrac{{54}}{7} = \dfrac{{84}}{7} = 12s$
Therefore the second collision occurs at $12s$ after the ball is released from a height of $90m$.
Using these above information, we get the velocity-time graph as,

However, we require the speed- time graph and not the velocity- time graph.
Thus we will only take the absolute values of the velocities and use them for drawing the graph.

Here we have made the plot till before the second collision occurs.
Note Here we have assumed the sign convention as negative towards the earth and positive away from the acceleration due to gravity. Thus the signed value of acceleration due to gravity is $g = - 9.8m/{s^2}$ which is directed towards the earth.
Recently Updated Pages
JEE Main Login 2025 - Step-by-Step Explanation

JEE Main 2025 Exam Date: Check Important Dates and Schedule

JEE Main 2025 City Intimation Slip: Downloading Link and Exam Centres

JEE Main 2025 Application Form Session 1 Out - Apply Now

JEE Main 2025 Registration Ends Today: Apply Now for January Session

JEE Main OMR Sheet 2025

Trending doubts
JEE Main 2025: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Class 11 JEE Main Physics Mock Test 2025

Angle of Deviation in Prism - Important Formula with Solved Problems for JEE

Average and RMS Value for JEE Main

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
NCERT Solutions for Class 11 Physics Chapter 7 Gravitation

NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Fluids

Units and Measurements Class 11 Notes - CBSE Physics Chapter 1

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line

Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (Free PDF Download)




