Question

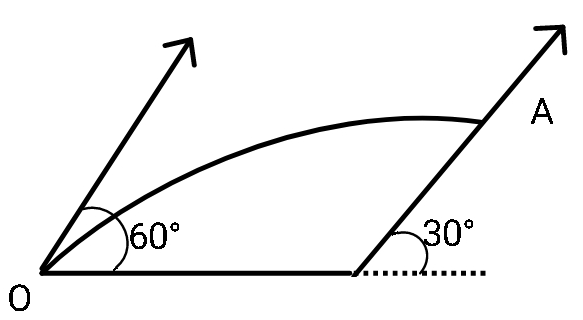
A ball is projected from the point O with velocity 20 m/s at an angle of 60° with the horizontal as shown in the figure. At the highest point of its trajectory, it strikes a smooth plane of inclination 30° at point A. The collision is perfectly inelastic. The maximum height from the ground is attained by the ball is

A. 18.75 m
B. 15 m
C. 22.5 m
D. 20.25 m

Answer 1

Hint: At the highest point of the trajectory of the ball, the ball will have no vertical component of velocity. As the collision is inelastic, the ball will not bounce back but with all its horizontal velocity, it will try to move some height up on the incline.
Formula used:
Maximum height of the trajectory:
$H = \dfrac{u^2 \sin ^2 \theta}{2 g}$
Third law of motion:
$v_f^2 - v_i^2 = 2 g h$

Complete answer:
First we determine the maximum height attained by the ball when it begins with initial velocity, u =20 m/s and is fired at an angle of 60$^{\circ}$ with the horizontal. Substituting the values in the formula we may write:
$H = \dfrac{(20)^2 (\sqrt{3} / 2)^2 }{2 \times 10} = 15 m$
Therefore, the ball attains a height of 15 m before its collision with the incline.
Now, the ball at a height of 15 m, has only horizontal component of its initial velocity sustaining. Let us denote the horizontal component as $u_x$, so that
$u_x = u \cos 60^{\circ} = 20 \times \dfrac{1}{2} = 10 $ m/s.
This is the velocity of the ball in horizontal direction, before colliding with the incline.
Now, refer to the following diagram and observe the velocity component that the ball will have along the incline.

The velocity of the ball as it starts along the incline can be written as:
$v = u_x \cos 30^{\circ} = \dfrac{10 \times \sqrt{3}}{2} = 5 \sqrt{3}$ m/s.
Now, we consider the point where the ball hits the incline to be ground. We write final v = 0 m/s in the third law of motion. Therefore we get the height that again the ball attains along the incline by using the formula:
$v_i^2 = 2 g h'$
$\implies h' = \dfrac{(5 \sqrt{3})^2}{2 \times 10} = 3.75 m$
here $v_i$ is the initial velocity of the ball that it has before starting to climb along the incline.

Therefore, the total height that the ball will attain will be 15 m + 3.75 m = 18.75 m.

So, the correct answer is “Option A”.

Note:
One might conclude the wrong answer if one thinks that after striking the inclined plane, the ball completely stops and drops to ground along the incline. In that case one might only find the maximum height of the ball along its trajectory and not the total height that ball attains including along inclined plane.