Question

A ball of mass 0.5 kg is attached to the end of a string having length 0.5 m. The ball is rotated on a horizontal circular path about the vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in \[rad{{s}^{-1}}\]) is –

A) 9
B) 18
C) 27
D) 36

Answer 1

Hint: We need to understand the relation between the tension experienced by a string and the angular velocity of the string when it is rotated about a vertical axis in order to solve the angular velocity to get the solution for this problem.

Complete answer:
We are given a situation in which a ball is suspended on a string which is fixed at one end and hangs down which can be rotated about this fixed point on the vertical plane. The tension that can be afforded by the string is 324 N.

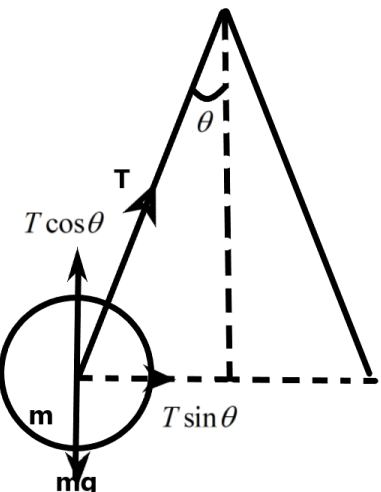
We know that the tension produced on the string is dependent on the mass of the ball, the angular velocity of the rotation and the radius of the rotation of the ball. The radius of the rotation is dependent on the angle subtended by the string with the vertical. It can be given as –
\[R=L\sin \theta \]
Where, L is the length of the string.
Now, we can find the maximum angular velocity that the string can afford using the relation between the tension and the angular momentum as –
\[\begin{align}
  & T\sin \theta =m{{\omega }^{2}}R \\
 & \Rightarrow T\sin \theta =m{{\omega }^{2}}L\sin \theta \\
 & \Rightarrow T=m{{\omega }^{2}}L \\
 & \Rightarrow \omega =\sqrt{\dfrac{T}{mL}} \\
 & \Rightarrow \omega =\sqrt{\dfrac{324}{0.5\times 0.5}} \\
 & \therefore \omega =36rad{{s}^{-1}} \\
\end{align}\]
So, the angular velocity which can be applied to the system such that the system is not destroyed is 36 radians per second.

The correct answer is option D.

Note:
We can see that the angular momentum which we equated to the tension is nothing but the force acting in the system due to the rotational torque. The force is dependent on the torque which is equivalent to the angular momentum in circular motion.