Question

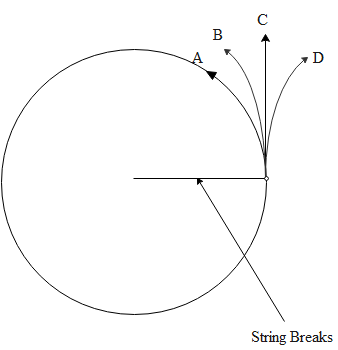
A ball on a string is swung in a vertical circle. The string happens to break when it is parallel to the ground and the ball is moving up. Which trajectory does the ball follow?

Answer 1

Hint: We should know that trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, the mass might be a projectile or a satellite. For example, it can orbit the path of a planet, asteroid, or comet as it travels around a central mass. Projectile motion is a form of motion where an object moves in a parabolic path. The path followed by the object is called its trajectory. The angle at which the object is launched dictates the range, height, and time of flight the object will experience while in projectile motion. Based on the concept we have to answer this concept.

Complete step by step answer
When a ball is swung on a string in a vertical circle, the tension is greatest at the bottom of the circular path. This is where the rope is most likely to break. It should make sense that the tension at the bottom is the greatest. Imagine watching the summer Olympics, specifically the gymnastics competitions.
When a gymnast is doing the parallel bars, spinning themselves around in a vertical circle, when does she have to struggle the most to keep hold of the bar? Not at the top. In fact, at the top the gymnast feels relief (and often repositions her hands). At the bottom, however, the gymnast's arms will hurt. Gymnasts are most likely to lose hold of the parallel bar when reaching the bottom of their circular path.
However, what happens if the ball on the string (or the gymnast, for that matter) isn't going very fast. Without enough speed, the ball won't be able to complete the circle. It will leave its circular path at the top, because the string will lose tension. So, a minimum velocity is needed for objects to complete vertical circles. Well if the ball "just barely" gets over the top of the circle, the tension in the rope.
As long as the ball moves faster than the ball will complete the circular loop. So, remember this: when talking about the rope breaking, use the bottom-of-the-loop equation. When talking about critical speed, use the top-of-the-loop equation, with tension set equal zero.

So, the ball will follow trajectory path C.

Note: When we launch a projectile, it follows a parabolic path. There is a horizontal component and a vertical component to its motion, and they can be studied separately. Horizontally, the projectile simply moves at the initial horizontal velocity, the horizontal component of the initial velocity until something stops it. Since relative acceleration is zero, relative velocity is constant and hence, the path of a projectile seen from another projectile is a straight line.
It should also be known to us that mass does not affect the speed of falling objects, assuming there is only gravity acting on it. Both bullets will strike the ground at the same time. The horizontal force applied does not affect the downward motion of the bullets, only gravity and friction or air resistance, which is the same for both bullets.