Question

A bird is flying at a height of 3.6m above the surface of water and a fish is in the water at a depth of 1.2m. The apparent height of the bird to the fish is (\[{\mu _{water}} = \dfrac{4}{3}\])
A. 3.9 m
B. 4.8 m
C. 5.2 m
D. 6.0 m

Answer 1

Hint:When the light ray travels from a rare medium to a denser medium, the path of light bends towards the normal. Due to the bending, the height of the bird will appear raised than the real height. The refractive index of the medium is the ratio of the apparent height to the real height.

Formula used:
\[\mu = \dfrac{{{h_A}}}{{{h_O}}}\]
Here, \[\mu \] is the refractive index of the medium, \[{h_A}\] is the apparent height of the object and \[{h_O}\] is the original height.

Complete step by step answer:
We know that when the light ray travels from a rare medium to a denser medium, the path of light bends towards the normal. The bending of light in the medium depends on the refractive index of the medium. Due to the bending of the light, the depth of the bottom surface of water appears changed. When the light ray from the bird travels from air to water it bends towards the normal and thus, the height of the bird appears raised to the fish. The following figure will ease our understanding.

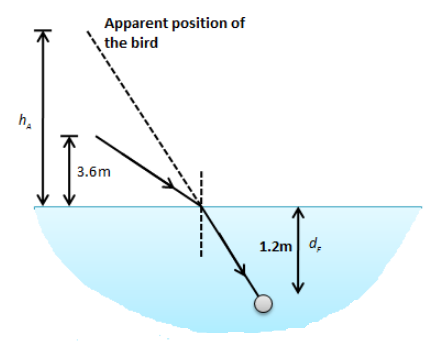
We can express the apparent height of the bird from the surface of water as,
\[\mu = \dfrac{{{h_A}}}{{{h_O}}}\]
Here, \[\mu \] is the refractive index of the water, \[{h_A}\] is the apparent height of the bird and \[{h_O}\] is the original height.
Substituting \[\mu = \dfrac{4}{3}\] and \[{h_O} = 3.6\,{\text{m}}\] in the above equation, we get,
\[\dfrac{4}{3} = \dfrac{{{h_A}}}{{3.6}}\]
\[ \Rightarrow {h_A} = 4.8\,{\text{m}}\]
This is the apparent height of the fish above the surface of the water. Therefore, the apparent height of the bird from the fish will be,
\[\therefore h = 4.8 + 1.2 = 6\,{\text{m}}\]
Thus, the apparent height of the bird to the fish is 6 m.

So, the correct answer is option D.

Note:If it is for the bird, the depth of the fish would appear different for the bird than the real depth due to the different refractive index of the water. While drawing the ray diagram, if the observer is the fish, the incident ray should be the light ray reflected from the bird towards the eye of the fish. Therefore, the incident ray travels from air to water. The opposite will be for the bird as an observer.