Question

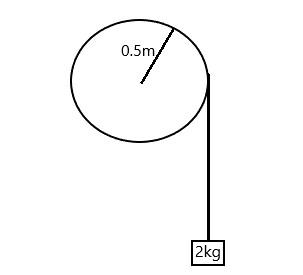
A block of mass 2 kg, hangs from the rim of a wheel of radius \[0.5\] m. On releasing from rest, the block falls through 5m height in 2s. the moment of inertia of the wheel is (take \[g = 10m/{s^2}\])

(A) \[1kg{m^2}\]
(B) \[3.2kg{m^2}\]
(C) \[2.5kg{m^2}\]
(D) \[1.5kg{m^2}\]

Answer 1

Hint: The acceleration of the block is the same as the linear acceleration of the rim. The tension in the string is the driver of the rim.
Formula used: In this solution we will be using the following formulae;
\[s = ut + \dfrac{1}{2}a{t^2}\] where \[s\] is the distance covered by an accelerating body, \[u\] is the initial velocity, \[a\] is the acceleration of the body, and \[t\] is the time elapsed.
\[Fr = I\alpha \] where \[F\] is the force acting on a body, \[r\] is the distance of \[F\] from an axis of rotation, \[I\] is the moment of inertia of the body and \[\alpha \] is the angular acceleration. The quantity, \[Fr\] is the torque on a body.
\[\alpha = \dfrac{a}{r}\] where \[a\] is the linear acceleration, and \[r\] is the radius of a body.

Complete Step-by-Step solution:
Generally, moment of inertial and the force acting on a body are related through
\[Fr = I\alpha \] where \[F\] is the force acting on a body, \[r\] is the distance of \[F\] from an axis of rotation, \[I\] is the moment of inertia of the body and \[\alpha \] is the angular acceleration.
Hence, to find the moment of inertia, we need to know the force of the rim and the angular acceleration.
Angular acceleration is \[\alpha = \dfrac{a}{r}\] where \[a\] is the linear acceleration, and \[r\] is radius.
The acceleration can be gotten from
\[s = ut + \dfrac{1}{2}a{t^2}\] where \[s\] is the distance covered by an accelerating body, \[u\] is the initial velocity, \[a\] is the acceleration of the body, and \[t\] is the time elapsed.
Hence,
\[5 = \dfrac{1}{2}a{\left( 2 \right)^2}\]
\[ \Rightarrow a = \dfrac{5}{2}m/s\]
Then
\[\alpha = \dfrac{{\dfrac{5}{2}}}{{0.5}} = 5rad/{s^2}\]
The force driving the rim is the tension, hence to calculate tension on string, we perform newton's law analysis on block
\[mg - T = ma\]
\[ \Rightarrow 2\left( {10} \right) - T = 2\left( {\dfrac{5}{2}} \right)\]
Hence,
\[T = 15N\]
Then,
\[Tr = I\alpha \]
\[ \Rightarrow 15(0.5) = I\left( 5 \right)\]
Then by dividing both side by 5, we have
\[I = \dfrac{{15\left( {0.5} \right)}}{5} = 2.5kg{m^2}\]

Hence, the correct option is C

Note: For clarity, the tension is the force which drives the rim because the string is the object directly in contact with the rim. The tension is as a result of the block hanging down, however it’s not the weight that drives it but the transmitted force along the string (which is the tension).