Question

A block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are ${a_1}$, ${a_2}$ and ${a_3}$ as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is ${x_0}$. Which of the following option(s) is/are correct? [g is the acceleration due to gravity. Neglect friction]

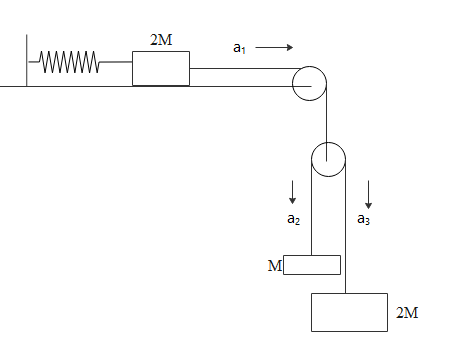
A. At an extension of ${x_0}/4$ of the spring, the magnitude of acceleration of the block connected to the spring is 3g/10
B. ${x_0}$ = 4 Mg/k
C. When spring achieves an extension of ${x_0}/2$ for the first time, the speed of the block connected to the spring is $3g\sqrt {\dfrac{M}{{5k}}} $
D. ${a_2} - {a_1} = {a_1} - {a_3}$

Answer 1

Hint: In case of simple harmonic motion there will be a mean position and two extreme positions. The particle executes the SHM with respect to the mean position and within the range of two extreme positions. Here the block on the surface executes simple harmonic motion.

Formula used:
$a = - {\omega ^2}\left( {x - {x_m}} \right)$

Complete step by step answer:
The block of mass 2M is connected to the spring and we will find out the acceleration of that block first.

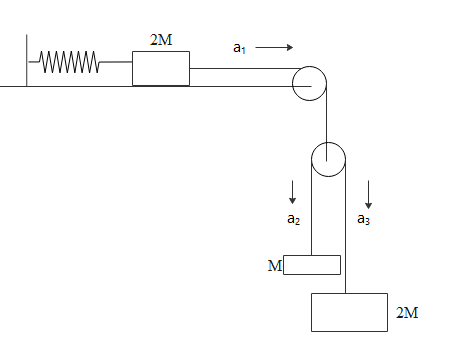
Accelerations of blocks hanging with respect to pulley must be equal.
So
${a_2} - {a_1} = {a_1} - {a_3}$
${a_2} - {a_1}$ is the relative acceleration of block M with respect to pulley
${a_1} - {a_3}$ is the relative acceleration of block 2M with respect to pulley
So option D is correct.
Tension in the string connecting two pulleys will be
$T = \dfrac{{2{m_1}{m_2}}}{{{m_1} + {m_2}}}\left( {g - a} \right)$
$\eqalign{
  & \Rightarrow T = \dfrac{{2M\left( {2M} \right)}}{{M + 2M}}\left( {g - a} \right) \cr
  & \therefore T = \dfrac{{4M}}{3}\left( {g - {a_1}} \right) \cr} $
$g - {a_1}$ is the net downward gravitational acceleration with respect to pulley.
Tension on the horizontal 2M block will be 2T
So
$2T - kx = 2M{a_1}$
$ \Rightarrow 2T = \dfrac{{8M}}{3}\left( {g - {a_1}} \right)$
$\eqalign{
  & \Rightarrow \dfrac{{8M}}{3}\left( {g - {a_1}} \right) - kx = 2M{a_1} \cr
  & \therefore {a_1} = \dfrac{{ - 3k}}{{14M}}\left[ {x - \dfrac{{8Mg}}{{3k}}} \right] \cr} $
Upper equation resembles the SHM equation $a = - {\omega ^2}\left( {x - {x_m}} \right)$
Where
${x_m}$ is the mean position distance from natural length position.
$\omega = \sqrt {\dfrac{{3k}}{{14M}}} $
Amplitude will be $A = \dfrac{{8Mg}}{{3k}}$
Hence ${x_0} = 2A = \dfrac{{16Mg}}{{3k}}$
So option B is wrong.
At $x = \left( {\dfrac{{{x_0}}}{2}} \right)$ block will pass through the mean position. Hence velocity will be
${v_0} = A\omega = \dfrac{{8Mg}}{{3k}}\sqrt {\dfrac{{3k}}{{14M}}} $
Hence option C is wrong
At
$\eqalign{
  & x = \dfrac{{{x_0}}}{4}{\mkern 1mu} \cr
  & \Rightarrow x = \dfrac{{\dfrac{{16Mg}}{{3k}}}}{2} \cr
  & \Rightarrow x = \dfrac{{4Mg}}{{3k}}{\mkern 1mu} \cr
  & \therefore x = \dfrac{A}{2}{\mkern 1mu} \cr} $
Acceleration at that position will be
$\eqalign{
  & a = \dfrac{A}{2}{\omega ^2} \cr
  & \therefore a = \dfrac{{4mg}}{{3k}}\left( {\dfrac{{3k}}{{14m}}} \right) = \dfrac{{2g}}{7} \cr} $
Hence option A is wrong.

Note: So, the correct answer is “Option D”.

Note:
This question can be seen as some mass hanging to the spring in the gravity. We will find the equilibrium position in that case which will be the mean position and amplitude will be the twice of mean position distance from the natural length and at extreme positions velocity will be zero but acceleration is maximum.