Question

A block of mass $m$ is changed by the means of a string which goes over a pulley of mass $m$ and the moment of inertia $I$, as represented in the diagram. The string does not move relative to the pulley. Calculate the frequency of the small oscillations.

Answer 1

Hint: Then the frequency of the small oscillation will be found by taking the product of $\dfrac{1}{2\pi }$ and the square root of the ratio of the spring constant to the mass of the system. Substitute the values in it by considering the equation by balancing the forces in it. This will help you in answering this question.

Complete answer:

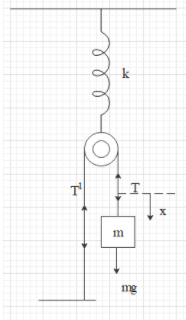
Suppose the block will be depressed by $x$. The pulley owing to the constant is depressed by $\dfrac{x}{2}$. Let us assume that the tension in the string is $T$ and ${T}'$ on both sides. Therefore we can write that,
For the block we can mention that,
$mg-T=mx$……… (1)
In the case of the pulley, we can write that,
$T+{T}'+mg-k\left( x+{{x}_{0}} \right)=m\dfrac{x}{2}$…………. (2)
Where $m$ be the mass of the block and $k$ be the spring constant.
The angular acceleration of the pulley can be found by taking the ratio mentioned as,
$\alpha =\dfrac{\dfrac{x}{2}}{2R}$………….. (3)
And also we can write that,
$\left( T-{T}' \right)R=l\dfrac{x}{2R}$……………. (4)
From the equations 1, 2, 3 and 4, we can write that,
$3mg-k\left( x+{{x}_{0}} \right)=\left( \dfrac{5m}{2}+\dfrac{l}{2{{R}^{2}}} \right)x$
Then the frequency of the small oscillation will be found by taking the product of $\dfrac{1}{2\pi }$ and the square root of the ratio of the spring constant to the mass of the system. That is we can write that,
$f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{\dfrac{5m}{2}+\dfrac{l}{2{{R}^{2}}}}}$
Therefore the frequency of the oscillation has been calculated.

Note:
Frequency of the oscillation can be defined as the number of oscillations completed in a unit period of time. The frequency is found to be the reciprocal of the time period. The unit of frequency has been found to be hertz.