Question

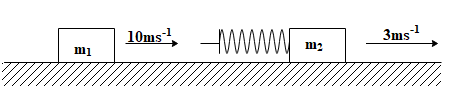
A block of mass ${{m}_{1}}=2kg$ slides on a frictionless table with speed of $10m{{s}^{-1}}$. In front of it, another block of mass ${{m}_{2}}=5kg$is moving with speed $3m{{s}^{-1}}$ in the same direction. A massless spring of spring constant $k=1120N{{m}^{-1}}$ is attached on the backside of ${{m}_{2}}$ as shown. Find the maximum compression of the spring in $cm$ when the blocks collide. (Take $g=10m{{s}^{-2}}$)
A.$50cm$
B.$25cm$
C.$35cm$
D.$100cm$

Answer 1

Hint:Collision of two bodies implies that their energies as well as momentum must change. However, the momentum and energy of the two bodies taken as one system will remain conserved. Therefore, we shall conserve the energy and momentum of the system also taking into consideration the energy of the spring compressing during the collision.

Complete answer:
Here, we consider block ${{m}_{1}}$, block ${{m}_{2}}$ and the spring as our system.
Since no external force is acting on the system, therefore we shall apply conservation of momentum on it. Hence, by conservation of momentum:
$\begin{align}
  & \Delta p=0 \\
 & \Rightarrow \Delta \left( mv \right)=0 \\
\end{align}$
$\Rightarrow $ initial momentum = final momentum
$\Rightarrow {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Where,
$u=$ initial velocity
$v=$ final velocity
We have ${{m}_{1}}=2kg,\text{ }{{m}_{2}}=5kg,\text{ }{{\text{u}}_{1}}=10m{{s}^{-1}},\text{ }{{\text{u}}_{2}}=3m{{s}^{-1}}$,
$\Rightarrow \left( 2 \right)\left( 10 \right)+\left( 5 \right)\left( 3 \right)=\left( 2+5 \right)v$
The final velocity of both the blocks is the same, that is, ${{v}_{1}}={{v}_{2}}$, because after collision both the blocks move together as one block.
$\begin{align}
  & \Rightarrow 20+15=7v \\
 & \Rightarrow v=\dfrac{35}{7} \\
\end{align}$
\[\therefore v=5m{{s}^{-1}}\]
\[\Rightarrow {{v}_{1}}={{v}_{2}}=5m{{s}^{-1}}\]
The change in kinetic energy of the blocks is stored as the spring energy in the compressed spring when force is applied on it during collision. Therefore, to conserve energy of the system, we equate the energy stored in spring during compression with the change in kinetic energy of the blocks during collision.
Energy stored in spring, ${{E}_{sp}}$ is given as:
${{E}_{sp}}=\dfrac{1}{2}k{{x}^{2}}$ …………………. Equation (1)
Where,
$k=$ spring constant
$x=$ change in length of spring (compression or elongation)
Change in kinetic energy = initial kinetic energy $-$ final kinetic energy
$\Rightarrow \Delta K.E.={{\left( K.E. \right)}_{initial}}-{{\left( K.E. \right)}_{final}}$
$\Delta K.E.=\left( \dfrac{1}{2}{{m}_{1}}u_{1}^{2}+\dfrac{1}{2}{{m}_{2}}u_{2}^{2} \right)-\dfrac{1}{2}\left( {{m}_{1}}+{{m}_{2}} \right){{v}^{2}}$ …………………. Equation (2)
Combining equations (1) and (2), we get
${{E}_{sp}}=\Delta K.E.$
$\Rightarrow \dfrac{1}{2}k{{x}^{2}}=\left( \dfrac{1}{2}{{m}_{1}}u_{1}^{2}+\dfrac{1}{2}{{m}_{2}}u_{2}^{2} \right)-\dfrac{1}{2}\left( {{m}_{1}}+{{m}_{2}} \right){{v}^{2}}$
Substituting the given data,
$\Rightarrow \dfrac{1}{2}1120{{x}^{2}}=\left( \dfrac{1}{2}2{{\left( 10 \right)}^{2}}+\dfrac{1}{2}5{{\left( 3 \right)}^{2}} \right)-\dfrac{1}{2}\left( 2+5 \right){{\left( 5 \right)}^{2}}$
$\begin{align}
  & \Rightarrow 1120{{x}^{2}}=\left( 200+45 \right)-7\left( 25 \right) \\
 & \Rightarrow 1120{{x}^{2}}=245-175 \\
 & \Rightarrow 1120{{x}^{2}}=70 \\
 & \Rightarrow {{x}^{2}}=\dfrac{7}{112} \\
\end{align}$
$\begin{align}
  & \Rightarrow {{x}^{2}}=0.0625 \\
 & \Rightarrow x=\sqrt{0.0625} \\
 & \Rightarrow x=0.25 \\
\end{align}$
Hence, the maximum compression of spring is $0.25m$ or $25cm$.

Therefore, the correct option is (B) $25cm$.

Note:
When we apply force on a body, work is done on it which results in its change in state of motion to produce displacement. This change in state of motion induces a change in the kinetic energy of the body, either it increases or decreases the kinetic energy. Therefore, the work done on a body is equal to its change in kinetic energy. This is generally known as the work-energy theorem.