Question

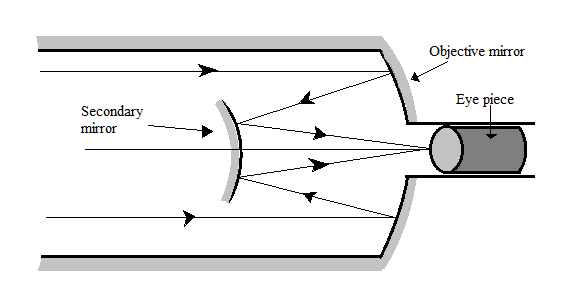
A Cassegrain telescope uses two mirrors as shown in the above figure. Such a telescope is built with the mirrors $20mm$ apart. If the radius of curvature of the large mirror is $220mm$ and the small mirror is $140mm$, where will the final image of an object at infinity be?

Answer 1

Hint:In order to solve this question you have to know the concept of mirror formula for concave and convex mirror. Always remember that when there is given a Cassegrain telescope like in above diagram then the image formed by the objective will act as a virtual object for the secondary mirror.

Formula used:
Mirror formula is given as
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Where $v$ is the distance where the final image formed
$u$ is the distance of the object from the mirror
$f$ is the focal length of the mirror

Complete step by step solution:
The distance between the objective mirror and the secondary mirror is given in the question, $d = 20mm$
The radius of the curvature of the objective mirror is also given in the question, ${R_1} = 220mm$
Hence, the focal length of the objective mirror is, ${f_1} = \dfrac{{{R_1}}}{2} = 110mm$
Also the radius of curvature of the secondary mirror is given in the question, ${R_2} = 70mm$
Hence, the focal length of the secondary mirror is, ${f_2} = \dfrac{{{R_2}}}{2} = 70mm$
The image formed by the objective mirror with an object placed at infinity, will act as a virtual object for the secondary mirror.
Hence, the image distance which acts as an object for the secondary mirror is,
$u = {f_1} - d$
On putting the values, we get
$ \Rightarrow u = 110 - 20 = 90mm$
Now, Applying the mirror formula for the secondary mirror,
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{{{f_2}}}$
On putting all the values, we get
$\dfrac{1}{v} + \dfrac{1}{{90}} = \dfrac{1}{{70}}$
On solving this we get
$ \Rightarrow v = 315mm$

Hence, the final image of an object at infinity will be formed $315mm$ away from the secondary mirror.

Note:The Cassegrain telescope is an reflecting astronomical telescope, in which light ray is incident on a concave mirror known as objective mirror and then the reflected ray incident on a smaller convex mirror known as secondary mirror and then finally this ray is also gets reflected through a hole in the concave mirror onto a eyepiece to finally form the image.