Question

A charged particle with charge $q$ is moving in a uniform magnetic field. If this particle makes any angle with the magnetic field then its path will be:
A. Circular
B. Straight line
C. Helical
D. Parabolic.

Answer 1

Hint: When a charged particle moves in a magnetic field it experiences a force. The direction of this force is perpendicular to the magnetic field and direction of motion of the charged body. So the charged body will deviate from its original path because of this force.
Formulas used:
When a charged particle having charge $q$ and velocity $\overrightarrow{v}$ enters a magnetic field $\overrightarrow{B}$, it experiences a force given by
$\overrightarrow{F}=q\left( \overrightarrow{v}\times \overrightarrow{B} \right)$ The direction of this force is perpendicular to the magnetic field and direction of motion of the charged body. Its magnitude is given by
$F=qvB\sin \phi $, where
$\phi =\text{ angle between }\overrightarrow{v}\text{ and }\overrightarrow{B}$

Complete answer:
The force on a charged particle moving in magnetic field is given by
$\overrightarrow{F}=q\left( \overrightarrow{v}\times \overrightarrow{B} \right)$ Or $F=qvB\sin \phi $
$\phi =\text{ angle between }\overrightarrow{v}\text{ and }\overrightarrow{B}$
Consider a uniform magnetic field $\overrightarrow{B}$ is acting along the positive x-axis. A particle of charge ‘q’ and mass ‘m’ enters the field $\overrightarrow{B}$with velocity $\overrightarrow{v}$inclined at an angle $\phi $with the direction of field.

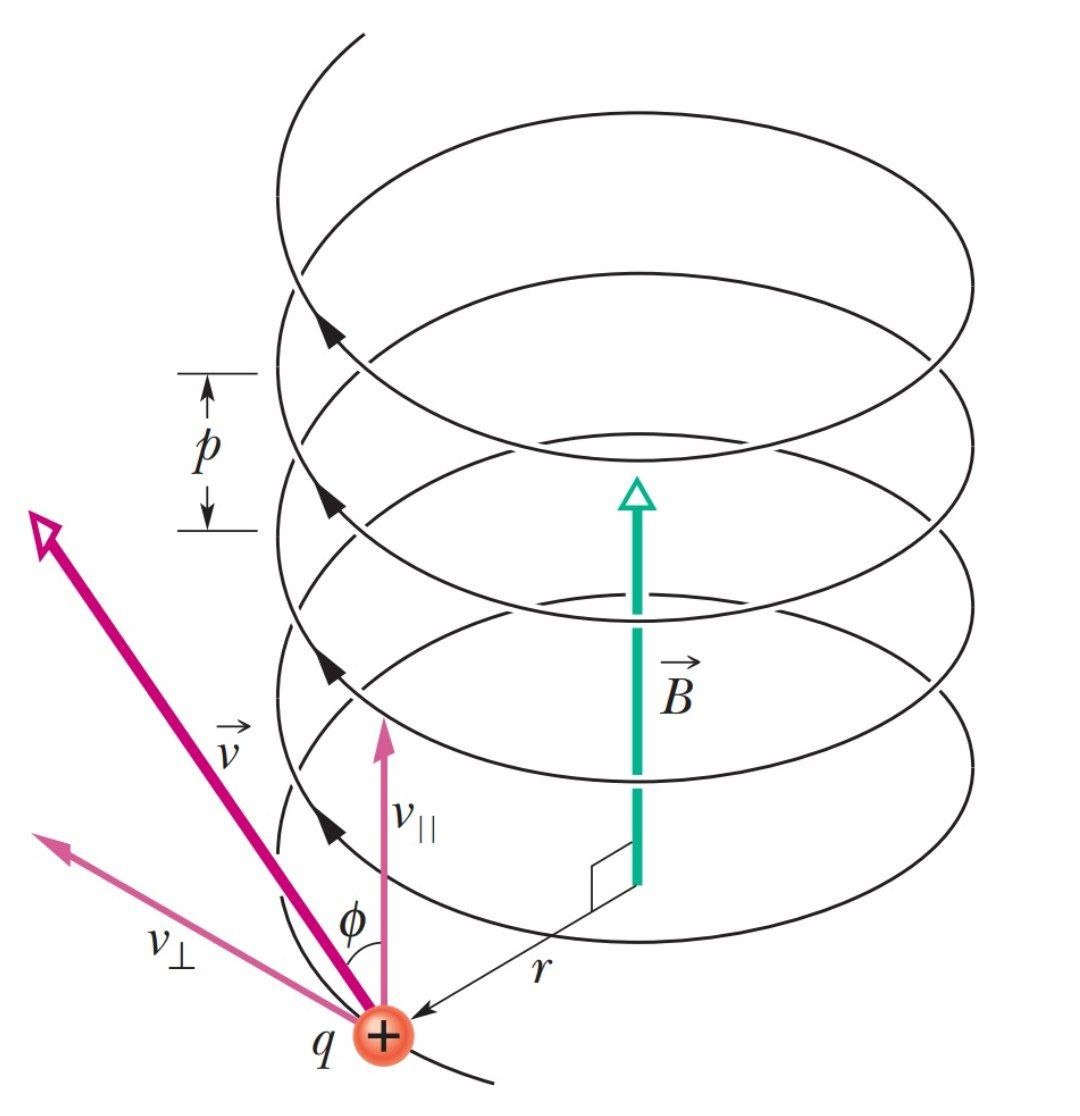
The velocity \[\overrightarrow{v}\] can be resolved into two rectangular components
(i) The component along parallel direction of field i.e. along x-axis which is given by
${{v}_{\parallel }}=v\cos \phi $
The parallel component remains unaffected by the magnetic field and so the charge particle continues to move along the field with the speed $v\cos \phi $.
(ii)The component perpendicular to the direction of field i.e. in the YZ-plane. And is given by
${{v}_{\bot }}=v\sin \phi $
Due to this component of velocity, the charged particle experiences a force $F=q{{v}_{\bot }}B$ which acts perpendicular to both ${{v}_{\bot }}$ and $B$. This force makes the particle move along a circular path in the YZ-plane. The radius of this circular path is.
$r=\dfrac{m{{v}_{\bot }}}{qB}=\dfrac{mv\sin \phi }{qB}$
The period of revolution is
$T=\dfrac{2\pi r}{{{v}_{\bot }}}=\dfrac{2\pi }{v\sin \phi }\times \dfrac{mv\sin \phi }{qB}=\dfrac{2\pi m}{qB}$
Thus a charged particle moving in uniform magnetic field has two concurrent motions
(i) A linear motion in the direction of the field
(ii)A circular motion in perpendicular to the field.
Therefore the resultant path of a charged particle will be a helix with its axis along the direction of the field.

So the correct option is C. Helical.

Note:
The linear distance travelled by the charge particle in the direction of magnetic field during its period of revolution is called pitch of the helical path and is given by.
$\text{pitch,p}={{v}_{\parallel }}\times T=v\cos \phi \times \dfrac{2\pi m}{qB}=\dfrac{2\pi mv\cos \phi }{qB}$.
A charged particle moving in a non-uniform field with initial velocity making some angle with the field will be also helical. But the path is not a uniform helix; it will be a non-uniform helix, with more radius in the region of more field.