Question

A circle is circumscribed about a trapezoid. Prove that this is possible if and only if the trapezoid is isosceles.

Answer 1

Hint: In this question circle is circumscribed about a trapezoid so we will first draw a diagonal lines in the trapezoid and then by SAS congruence theorem we will prove the obtained triangles to be congruent and then we will prove base angles are equal.

Complete step-by-step answer:
The trapezoid which is in the circle be PQRS, where PQ and RS are the bases and the PS and QR are the lateral sides as shown in the figure below

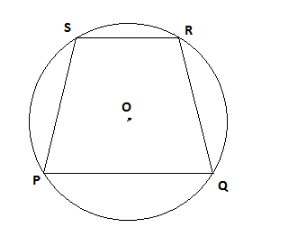
Now draw diagonals of the trapezoid PR and QS

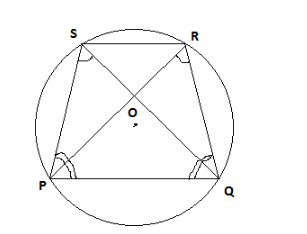
Now by drawing the diagonal of the trapezoid PR and QS, we get the triangles \[\Delta PQR\] and \[\Delta PQS\], where these two triangles have the common base PQ and the congruent sides QR and PS, since the trapezoid PQRS is isosceles.
Now we can say that \[\angle QPS\]and \[\angle PQR\] are congruent since the base PQ are congruent of the isosceles trapezoid.
Hence we can say \[\Delta PQR \simeq \Delta PQS\] (By SAS triangle congruence)
So we can say \[\angle PRQ \simeq \angle PSQ\] [since the \[\Delta PQR\] and \[\Delta PQS\]are congruent]
Hence we can say if the trapezoid is inscribed in a circle then the trapezoid is isosceles.

Note: Isosceles trapezoid is different from the general (standard) trapezoid in the way that an isosceles trapezoid is a trapezoid in which the base angles are equal and also the length of left and right side are equal.