Question

A circle of radius 7 cm is scaled 3 times. Then the perimeter of the circle become:
$\left( A \right)$ 3 times the original perimeter.
$\left( B \right)$ 6 times the original perimeter.
$\left( C \right)$ 9 times the original perimeter.
$\left( D \right)$ Doesn’t change.

Answer 1

Hint – In this particular question use the concept that a circle is a 2-D figure so the perimeter of the circle is equal to the circumference of the circle so use this concept to reach the solution of the question.

Complete step-by-step answer:
Given data:
Circle having radius 7 cm.
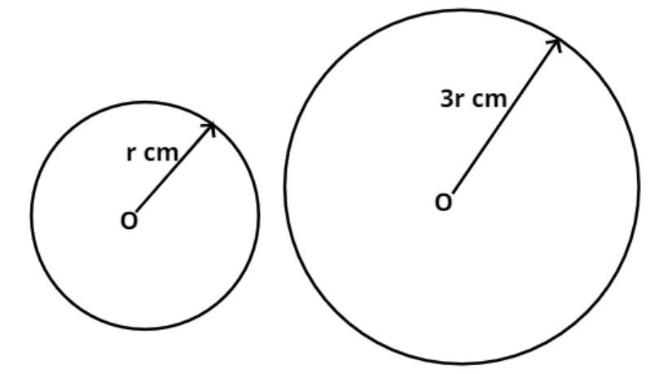
Let the radius of this circle be denoted by r cm (as shown in the figure).
Therefore, r = 7 cm.
Now it is given that the radius of the circle is scaled by 3 times.
So the new radius of the circle is 3 times the previous radius of the circle.
Let the new radius of the circle be denoted by R.
Therefore, R = 3r cm (as shown in the figure).
Now as we know that the perimeter of any shape is the sum of all the side lengths of the shape.
In the case of the circle as a circle is a 2-D figure so the perimeter of the circle is the circumference of the circle.
Now we all know that the circumference of the circle is given as $\left( {2\pi r} \right)$
So the circumference/perimeter of the smaller circle having radius r is
$ \Rightarrow {C_1} = 2\pi r$cm
$ \Rightarrow {C_1} = 2 \times \dfrac{{22}}{7} \times 7 = 44$ cm.................. (1)
Now the circumference/perimeter of the bigger circle having radius 3r is
\[ \Rightarrow {C_2} = 2\pi \left( {3r} \right)\]cm
Now simplify this we have,
\[ \Rightarrow {C_2} = 3\left( {2\pi r} \right)\].................. (2)
Now from equation (1) and (2) we have,
\[ \Rightarrow {C_2} = 3\left( {44} \right) = 132\] Cm.
So the perimeter of the circle whose radius is scaled three times the radius of the original circle is also three times the original perimeter.
So this is the required answer.
Hence option (A) is the correct answer.

Note – Whenever we face such types of questions the key concept we have to remember is that always recall the formula of the circumference of the circle which is stated above, then first calculate the circumference of the smaller circle as above then calculate the circumference of the bigger circle then check the circumference/perimeter of the bigger circle is how much times the original perimeter which is the required answer.