Question

A circular disc of area ${{A}_{1}}$ is given; with its radius as the diameter of a circular disc of area ${{A}_{2}}$ is cut out. If the area of the remaining disc is denoted by ${{A}_{3}}$, then
(a) ${{A}_{1}}{{A}_{3}}<16A_{2}^{2}$
(b) ${{A}_{1}}{{A}_{3}}>16A_{2}^{2}$
(c) ${{A}_{1}}{{A}_{3}}=16A_{2}^{2}$
(d) ${{A}_{1}}{{A}_{3}}>2A_{2}^{2}$

Answer 1

Hint: Here, we will assume that the radius of the disc with area ${{A}_{1}}$ is R and then we will try to find the value of ${{A}_{2}}$ and ${{A}_{3}}$ in terms of R. After that we can try to check which of the relations provided in the option is the correct.

Complete Step-by-Step solution:

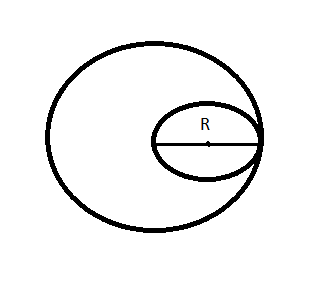
Let us consider that the radius of the circular disc whose area is ${{A}_{1}}$ is = R.
We know that the area of a disc is given by the formula $A=\pi \times {{\left( radius \right)}^{2}}$.
So, for the area of first disc we have:
${{A}_{1}}=\pi {{R}^{2}}............\left( 1 \right)$
Now, another disc whose area is ${{A}_{2}}$ is cut out from the disc of area ${{A}_{1}}$ as the radius of the second being the diameter of the first.
There, radius of the disc with area ${{A}_{2}}$ will be = $\dfrac{R}{2}$
So, for this disc area will be given as:
${{A}_{2}}=\pi \times {{\left( \dfrac{R}{2} \right)}^{2}}=\dfrac{\pi {{R}^{2}}}{4}............\left( 2 \right)$
Since, the area of the remaining disc is given as ${{A}_{3}}$ . So, we can write:
${{A}_{3}}={{A}_{1}}-{{A}_{2}}.............\left( 3 \right)$
On substituting the values of ${{A}_{1}}$ and ${{A}_{2}}$ from equation (1) and (2) in equation (3), we get:
$\begin{align}
  & {{A}_{3}}=\pi {{R}^{2}}-\dfrac{\pi {{R}^{2}}}{4} \\
 & \Rightarrow {{A}_{3}}=\dfrac{4\pi {{R}^{2}}-\pi {{R}^{2}}}{4}=\dfrac{3\pi {{R}^{2}}}{4} \\
\end{align}$
Now, to check the relations given in the options, we have to first find the values of ${{A}_{1}}{{A}_{3}}$.
We know that ${{A}_{1}}=\pi {{R}^{2}}$ and ${{A}_{3}}=\dfrac{3\pi {{R}^{2}}}{4}$.
Therefore, ${{A}_{1}}{{A}_{3}}=\pi {{R}^{2}}\times \dfrac{3\pi {{R}^{2}}}{4}=\dfrac{3{{\pi }^{2}}{{R}^{4}}}{4}$.
Also, we have to find the value of $16A_{2}^{2}$.
Since, ${{A}_{2}}=\dfrac{\pi {{R}^{2}}}{4}$.
Therefore, $16A_{2}^{2}=16\times \dfrac{{{\pi }^{2}}{{R}^{4}}}{16}={{\pi }^{2}}{{R}^{4}}$
Now, it is clear that $\dfrac{3{{\pi }^{2}}{{R}^{4}}}{4}<{{\pi }^{2}}{{R}^{4}}$.
So, ${{A}_{1}}{{A}_{3}}<16A_{2}^{2}$.
Now, to check for the last option, we have to calculate the value of $2A_{2}^{2}$ .
So, $2A_{2}^{2}=2\times {{\left( \dfrac{\pi {{R}^{2}}}{4} \right)}^{2}}=\dfrac{{{\pi }^{2}}{{R}^{4}}}{8}$
Since, $\dfrac{3{{\pi }^{2}}{{R}^{4}}}{4}>\dfrac{{{\pi }^{2}}{{R}^{4}}}{8}$
So, we have ${{A}_{1}}{{A}_{3}}>2A_{2}^{2}$.
Hence, option (a) and option (d) are the correct answers.

Note: Students should note here that we use the formula for the area of a circle to find the area of the disc. Students should be careful while comparing the area as they are in fractions to avoid unnecessary mistakes.